LiDAR安置误差对定位精度影响分析

丁 琼,吕俊涛,陈高文,詹晓彬

(广东工业大学 土木与交通工程学院，广东 广州 510006)

LiDAR安置误差对定位精度影响分析

丁 琼,吕俊涛,陈高文,詹晓彬

(广东工业大学 土木与交通工程学院，广东 广州 510006)

机载LiDAR为复杂的多传感器集成系统，系统误差是影响LiDAR定位精度的主要误差源.本文基于LiDAR定位方程，模拟往返航飞轨迹和激光脚点数据，定量地引入安置平移和安置旋转误差，研究各个系统误差对定位精度的影响程度和规律.实验结果表明安置平移误差对激光脚点定位精度的影响在对应方向有等量影响，而安置旋转误差对定位精度的影响在对应方向与扫描角相关.

LiDAR； 安置误差； 定位精度

机载LiDAR (Light Detection and Ranging) 作为一种全新的空间对地观测技术，能直接、快速地获取研究对象表面大量高精度的三维坐标点，在地形测绘、环境监测、城市建模、森林生物量统计、快速应急响应等方面有着巨大的优势.该技术与其他遥感技术相比具有主动性强、自动化程度高、受天气影响小、实时性强等特点，是近年来蓬勃发展起来的一种新型观测手段和方法，具有相当大的发展潜力[1-4].

由于机载LiDAR集成多个子系统，其定位精度受到系统集成误差、GPS定位误差、定向、测距等各类因素的影响，导致获取的点云数据与实际位置存在差异，降低了数据精度.为了获取高精度高质量的数据，必须研究这些误差的大小和影响规律并采取措施来消除或减小系统误差.因此，如何消除或减弱系统误差的影响，提高LiDAR的定位精度是目前机载LiDAR领域面临的一个重要问题[5].由于机载LiDAR的定位原理、作业方案、数据处理等均不同于传统的摄影测量与遥感系统，使得其消除误差的方法有别于传统的处理方法.目前，已有的系统误差消除方法主要有两类：一类是基于点云数据本身的航带平差[6-9]，该方法是将点位偏差和航带变形视为各类误差源综合作用的结果，并通过平差的方法使得重叠区域航带差异最小化，来实现系统误差的消除；另一类是基于传感器校检的航带平差[10-13]，该方法主要通过测量航带重叠区域同名特征的偏移，采用严密的几何定位方程建立误差模型，根据点云偏差求解传感器物理参数值.

因此，要消除系统误差，必须首先对各项系统误差本身有深刻的认识和理解.本文主要基于雷达定位方程，从理论上分析安置误差对定位精度的影响及其规律，为后期分析数据质量及数据检校提供参考.

1 LiDAR定位原理

LiDAR系统是由GPS、IMU和激光扫描测距仪3个子部件组成的.其中GPS提供平台位置信息，IMU提供姿态信息，激光扫描仪提供扫描中心到地面点的距离信息.其定位原理如图1所示.

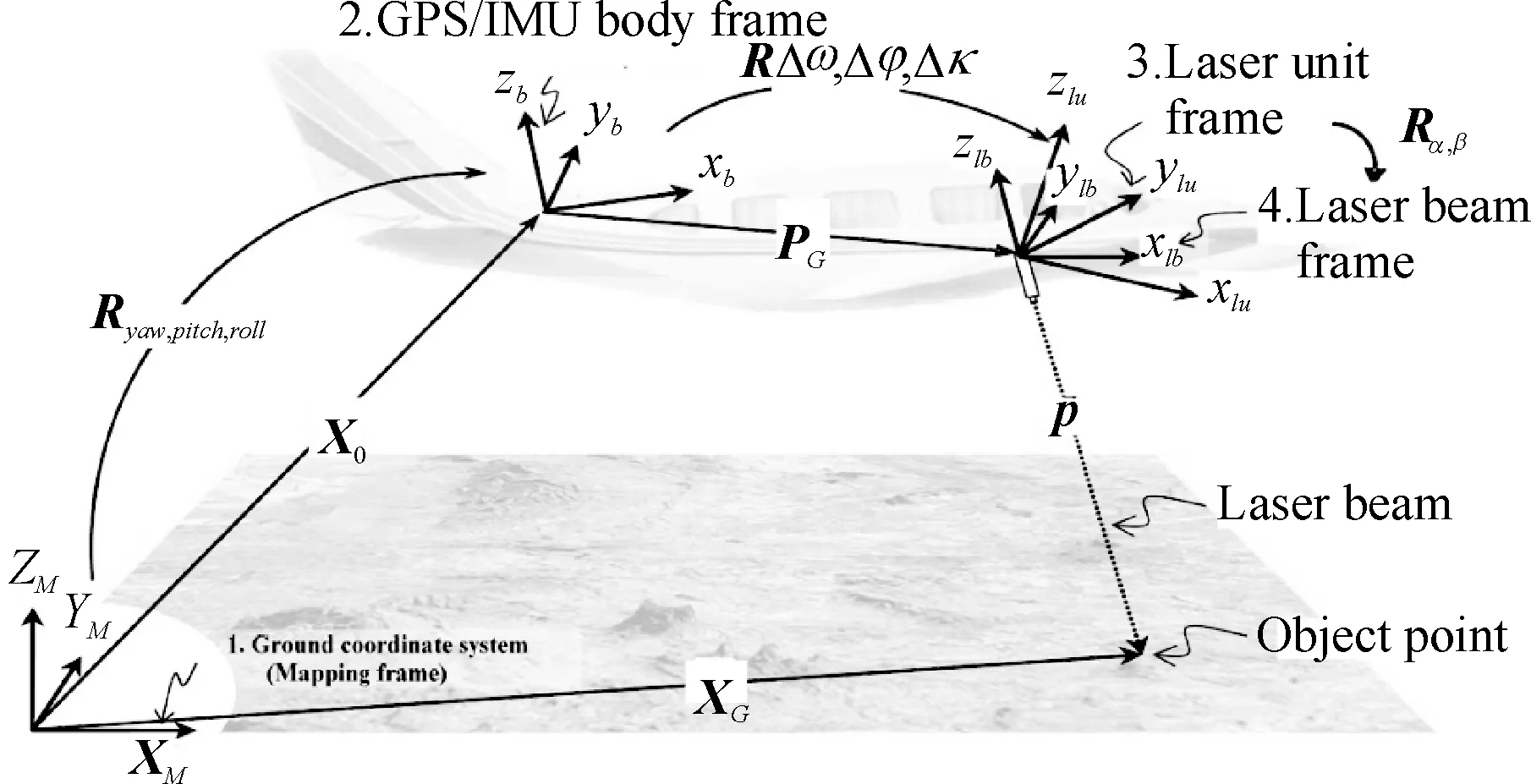
图1 机载LiDAR定位原理示意图[14-15]

定位方程[14-15]为

XG=X0+

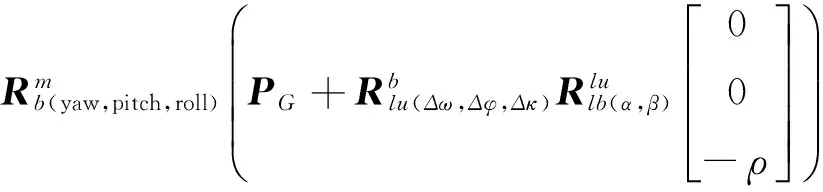
(1)

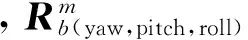
结合3个子系统获取的数据信息，就可以准确计算出每一个激光脚点的地面坐标，而大量的激光脚点聚集成激光点云(PointClouds).

2 实验方案

传统的安置误差指由于安装工艺上的限制，惯性测量单元坐标系和激光扫描坐标系不能完全重合及不平行而导致存在微小的位置和方向偏差，进而对定位精度产生影响.本次实验研究的系统误差包括安置平移误差ΔX,ΔY,ΔZ，安置旋转角误差Δω,Δφ,Δκ.具体步骤如图2所示.

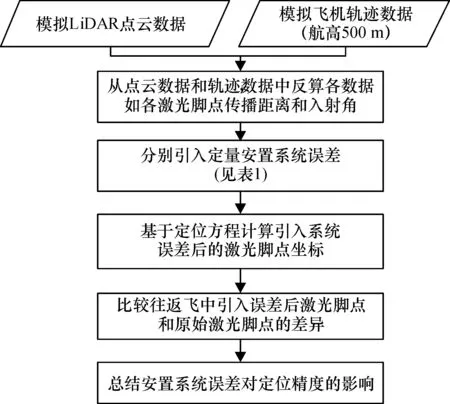
图2 实验流程图

首先，模拟给定的地平面和飞机轨迹，反算出系统观测值，包括每一个激光脚点的距离、扫描角、定位和定向信息.然后对研究的系统参数引入定量误差，生成带有误差的新坐标点.最后与不含误差的激光脚点进行比较，分析各个系统误差对激光脚点在3个方向上的影响及大小，并总结系统误差与地面点坐标精度之间的关系及规律.

本次实验基于往返飞两条模拟航带，并提取其中一条扫描线进行分析.假定GPS坐标系和地面坐标系平行，GPS中心和laser中心为一体，即，PG为0，且公式(1)中

(2)

其中，±分别对应往返飞行，引入误差后，地面点的定位方程可简化为

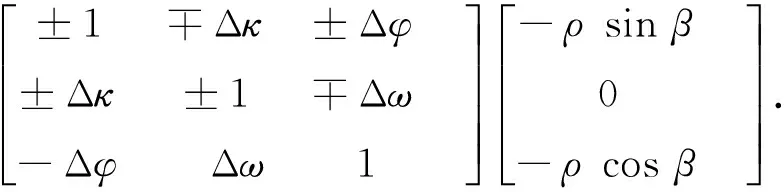
(3)

其中，XU为带有误差的地面激光脚点坐标，X0为GPS天线相位中心到地面坐标系之间的矢量，ΔX,ΔY,ΔZ为安置平移量误差，Δω,Δφ,Δκ为安置旋转量误差，ρ为激光光束传播的距离，β为激光扫描角.

引入的各项系统误差及其大小如表1所示.

3 实验结果分析

实验模拟500 m航高下，飞机往飞和返飞采集的两条扫描线，其扫描方向垂直于飞行方向，扫描角范围为30°.定量引入表1中所示6个系统误差后，激光脚点在X,Y,Z方向的影响如图3所示.

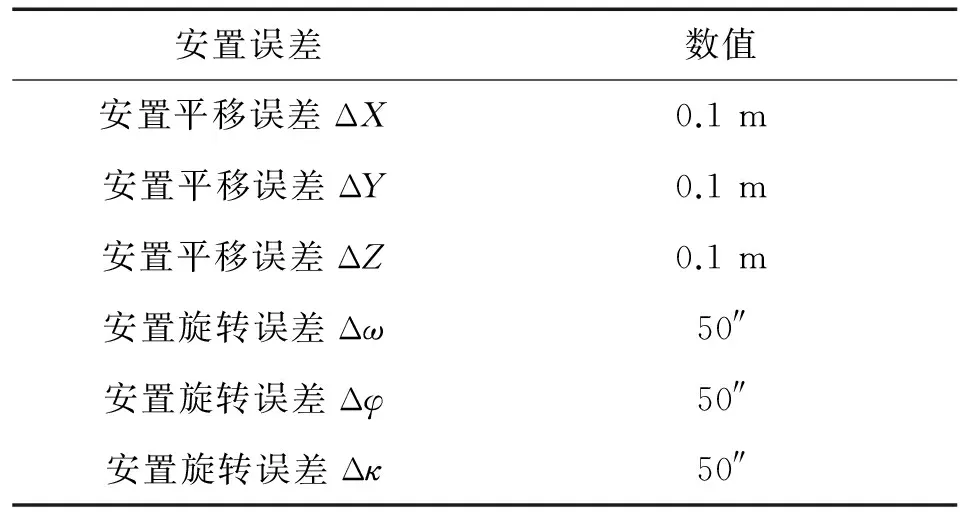
表1 引入的安置误差

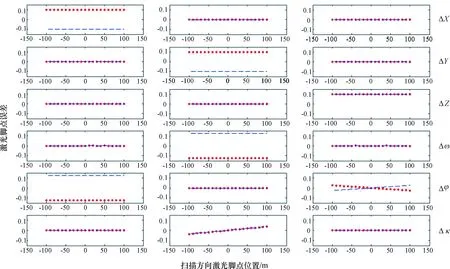
图3 各安置误差项对定位精度的影响

图3中，每行的3个子图对应一误差项在X,Y,Z3个方向上的差异，圆点线段和虚线段为往飞和返飞获取的激光脚点位置.横坐标为激光脚点沿垂直飞行方向所在的位置，原点位于飞机顶底；纵坐标为引入误差后激光脚点与原始脚点之间的差异.

从以上模拟结果可得以下结论.

(1) 安置平移量ΔX的误差对激光脚点的影响仅在X方向，且误差大小与安置误差等量，往返飞误差方向相反；在Y、Z方向无影响.

(2) 安置平移量ΔY的误差对激光脚点的影响在Y方向，且误差大小和安置误差等量，往返飞造成的影响相反；在X、Z方向无影响.

(3) 安置平移量ΔZ的误差对激光脚点的影响在Z方向，且误差大小和安置误差等量，往返飞造成的影响相同；在X、Y方向无影响.

(4) 安置旋转量仰俯角Δω的误差仅对激光脚点在Y方向产生影响，误差大小沿着扫描线方向一致，往返飞造成的影响相反；在X、Z方向无影响.

(5) 安置旋转量侧滚角Δφ的误差对激光脚点在X和Z方向产生影响，在Y方向无影响，X方向误差大小沿着扫描线方向一致，而Z方向的误差随着扫描角的增加而增大，往返飞造成的影响相反.

(6) 安置旋转量航偏角Δκ的误差仅对Y方向定位精度有影响，在X、Z方向无影响，Y方向定位精度随着扫描角的增加而降低，往返飞造成的影响相同.

4 结语

LiDAR系统误差是影响数据精度的主要误差源之一，必须对系统误差进行严格的校正以期提高LiDAR定位精度.本文基于LiDAR定位模型，模拟往返航飞数据并定量地引入安置平移和安置旋转误差，推导了各项误差对地面激光脚点精度的影响,总结了安置系统误差对定位精度的影响及其规律，进而为后期数据处理及有针对性的系统误差检校提供参考.

[1] Ackermann F. Airborne laser scanning-present status and future expectations[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2-3):64-67.

[2] Baltsavias E. Airborne laser scanning: existing systems and firms and other resources[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2-3):164-198.

[3] 张小红. 机载激光雷达测量技术理论与方法[M].武汉：武汉大学出版社, 2007.

[4] 李清泉, 李必军. 激光雷达测量技术及其应用研究[J]. 武汉测绘科技大学学报, 2000, 25(5): 387-392.

Li Q Q, Li B J. LiDAR technology and applications[J]. Geomatics and Information Science of Wuhan University, 2000, 25(5): 387-392.

[5] 成枢, 张艳亭, 马浩, 等. 国产机载LiDAR安置角误差检校初探[J]. 测绘通报, 2013, 1:37-40.

Cheng S, Zhang Y T, Ma H, et al. Research on boresight mislignment calibration of domestic airborne LiDAR[J]. Bulletin of Surveying, 2013, 1:37-40.

[6] Vosselman G. Strip offset estimation using linear features[C]∥In 3rd International Workshop on Mapping Geo-Surfical Processes using Laser Altimetry. USA,Columbus, Ohio:[s.n.], 2002.

[7] Pfeifer N, Elberink S O, Filin S. Automatic tie elements detection for laser scanner strip adjustment[J]. International Archives Photogrammetry and Remote Sensing, 2005, 36( 3/W3):1682-1750.

[8] Lee J, Yu K, Kim Y et al. Adjustment of discrepancies between LiDAR data Strips using linear features[J]. IEEE Geoscience and Remote Sensing Letter, 2007,4(3):475-479.

[9] Habib A F, Bang K I, Kersting A P, et al. Error budget of LiDAR systems and quality control of the derived data[J]. Photogrammetric Engineering and Remote Sensing, 2009,75(9):1093-1108.

[10] Filin S. Recovery of systematic biases in laser altimetry data using natural surfaces[J]. Photogrammetric Engineering and Remote Sensing, 2003,69(11):1235-1242.

[11] Habib A F, Bang K I, Shin S W, et al. LiDAR system self-calibration using planar patches from photogrammetric data[C]∥The 5th International Symposium on Mobile Mapping Technology.Italy, Padua:[s.n.],2007.

[12] 张靖, 江万寿, 姜三. 基于虚拟点模型的机载LiDAR系统自动检校方法[J]. 测绘学报, 2013, 42(3): 389-396.

Zhang J, Jiang W S, Jiang S. Automated airborne LiDAR system calibration using virtual tie point mode[J]. Acta Geodaeticaet Cartographica Sinica, 2013, 42(3):389-396.

[13] 张恒, 冯德俊, 马浩. 国产Lair-Lidar单机检校与试验研究[J]. 测绘通报, 2014(1):125-128.

Zhang H, Feng D J, Ma H. A study on calibration and test of domestic single lair-lidar instrument[J]. Bulletin of Surveying and Mapping, 2014(1):125-128.

[14] EL-Sheimy N, Valeo C, Habib A. Digital Terrain Modeling: Acquisition, Manipulation and applications[M]. US: Artech House,2005:257.

[15] Schenk T. Modeling and recovering systematic errors in airborne laser scanners[Z]. Columbus: The Ohio State University,2001.

Influence of LiDAR Systematic Error on Positioning Accuracy

Ding Qiong, Lü Jun-tao, Chen Gao-wen, Zhan Xiao-bin

(School of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou 510006, China)

Airborne LiDAR is multi-sensor system. Systematic error is a main error which affects LiDAR positioning accuracy. This paper simulates flight trajectory and laser footprints based on LiDAR positioning equation. Boresight errors are introduced to analyze the relationship between LiDAR systematic error and positioning accuracy. Results show that lever arm biases have the same impact on the accuracy of laser footprint while boresight angle biases have relationship with scanning angles on the positioning accuracy.

light detection and ranging (LiDAR); boresight error; positioning accuracy

2014- 11- 27

中国博士后科学基金资助项目(2014M552176);大学生创新创业训练计划项目(yj201311845054);广东工业大学博士启动项目(14ZK0014)

丁 琼(1983-)，女，讲师，博士，主要研究方向为机载LiDAR高精度数据处理和算法分析等.

10.3969/j.issn.1007- 7162.2015.03.021

P231

A

1007-7162(2015)03- 0115- 04