岩石阻容频散特性及其与流体饱和度关系研究

刘红岐, 邓友明, 田杰, 邱春宁

(1.油气藏地质与开发国家重点实验室, 四川 成都 610500;2.西南石油大学地球科学与技术学院, 四川 成都 610500)

0 引 言

激电方法以岩石电阻率的频谱或时谱特性差异为基础,测量大地的复电阻率频谱或时谱,寻找电性异常体,并根据描述岩石频谱或时谱参数进行评价,从而解决地质问题。Pelton等分别于1978年发表文献[1]、文献[2],奠定了电阻率法勘探的基础[1-2]。斯伦贝谢公司在1980年前后推出了1.1 GHz介电测井仪用以测量计算含水饱和度,但由于对岩石介电极化的机理并没有深入的研究,介电常数影响因素众多,该仪器在油田没有得到广泛应用[3]。国外重点对介电常数与岩石孔隙结构、润湿性、饱和度、矿化度以及渗透率等岩石物性参数进行了研究,都取得了很好的研究成果[4-12]。2008年,斯伦贝谢公司推出了新一代介电测井仪器,其仪器频率测量范围在MHz～GHz区间,用以区分离子极化、电子极化、位移极化等几种极化方式,提高了含水饱和度参数的评价效果[13]。在中国,唐炼等[14]在1994年公布了其在250 Hz～1.1 GHz区间内对大庆油田泥质砂岩的测量结果,认为在250 Hz～1.1 GHz范围内,干岩样的介电损耗可以忽略,在1.1 GHz的频率下,地层水矿化度对介电常数的实部影响小,但是对其虚部影响很明显,而介电常数与饱和度的关系为分段函数,当饱和度小于0.9时,介电常数与饱和度的关系为线性关系,饱和度大于0.9时,介电常数与饱和度的关系近似为二次多项式关系,与孔隙度的关系也不是线性关系。1997年胜利油田和美国EMI公司合作,开展了井间电磁成像系统的应用研究,在井中进行实际测量,采集到了高精度、高质量的井间电磁数据,并且利用这些数据进行轴对称二维反演[15],以此研究电磁场参数与岩石物性参数之间的关系。魏宝君、张庚骥等[16-17]利用体积分方程的改进型局域非线性方法,进行了井间三维电磁场正反演研究。陈序三、高杰、王伟男等[18-20]还开展了利用井中电性资料反演得到地下异常体复电阻率及其参数,为油气地质解释提供帮助,较好地反映地层的含油性;童茂松等[21-23]认为在低频测量情况下,与岩石的激发极化特性有关的复电阻率参数,如时间常数τ、频率相关系数c等与岩石孔隙结构和渗透率有非常密切的关系。在理论方法和实验研究的同时,柯式镇等[24-26]认为复电阻率测井仪是在原有的双侧向测井仪基础上改造而成,能够分别测量2个高低不同的频率信号区分流体信息,计算储层参数。

以上对介电常数的研究表明,介电常数含有丰富的信息,它与岩石的孔隙结构、孔隙度、饱和度、矿化度、渗透率等储层物性参数有着各种复杂的关系。深入研究介电常数所包含的信息,将可能为电法测井提供新的思路。本文在前人研究的基础上,通过岩心实验测试,重点讨论了Hz～MHz频率范围内,岩石电容率和其含水饱和度的关系。

1 实验测量

1.1 实验概述

选取砂岩1块、灰岩1块,共2块待测样品。在实验中采用全直径岩心进行测量,岩心的规格为高15 cm,直径10 cm的圆柱体,在其中间钻孔,称之为中孔,中孔直径为1.5 cm。实际测量时,将电极放置在内孔中,为保证电流传播,中孔内注满泥浆。这样的测量方式与现场经验测量方式很接近,其优点:①采取中孔测量方式,与井眼电法测井很相似,可以使电场由井眼中心向四周全方位均匀扩散,达到电场均匀分布的目的;②传统的在岩心两端放置夹持器,再连接电源的测量方式增加了电极与岩心之间的接触电阻,会引起系统误差。

1.2 测量电极

采用自制的适应不同环境的碳纤维电极进行测量,均设计为两电极型,较细的电极可以满足全直径岩心的测量(见表1)。

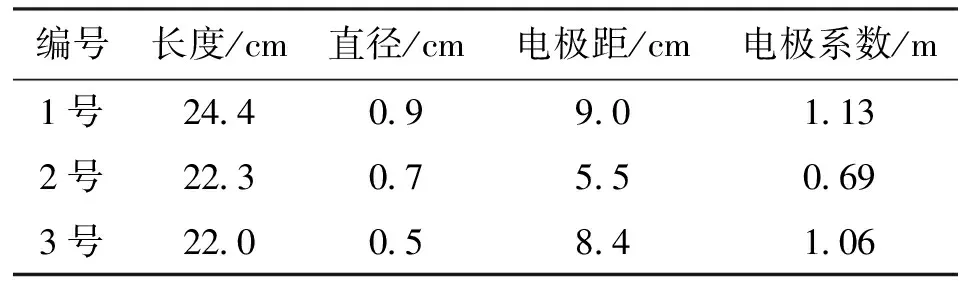
表1 碳纤维电极的规格

1.3 测量过程

①配制盐溶液。采用工业NaCl配置浓度为0.5 mol/L的溶液对岩样进行饱和。②进行岩心基础参数测量,包括岩心重量(干重)、体积、孔隙度、渗透率等基本参数(见表2)。③对岩心抽真空加压饱和。将岩心放入BH-II型高温高压真空饱和仪,在压力为30 MPa、真空度为-0.092 MPa条件下进行加压饱和13～24 h,待岩心100%饱和后,开始测量全饱和时的岩心电阻和电容参数。④进行岩心烘干测量。将岩心放入微波炉进行烘干,在中火条件下烘干5 min,取出岩心,测量其重量,计算其饱和度,然后连接LCR仪器进行测量。⑤重复以上步骤,直到相邻2次岩心重量相差2 g为止。

对13号砂岩烘干6次,每次岩样的重量和含水饱和度见表3。2种情况会导致盐溶液在离心后分布不均匀。一是如果岩心轴向较长,比如试验中岩心长度15 cm,由于远离圆心与靠近圆心受力不均导致盐溶液分布不均匀;另一种情况,在离心机将要结束的时候,离心速度逐渐降低,也会导致溶液分布不均匀,这些都会影响岩心电参数的测量。

表2 岩样基础参数

表3 13号砂岩烘干后参数表

2 数据测量与分析

2.1 岩心电阻率、电容率频散与饱和度关系分析

实验中,测量频率范围4 Hz～5 MHz。对砂岩进行了6次烘干测量,对灰岩进行了4次烘干测量。每次烘干后,分别测量了岩心在不同饱和度下的电阻和电容参数,根据1号电极的电极系数,将电阻和电容分别转换为电阻率和电容率。对应每次烘干所测数据分别记为R1,R2,…,R6;C1,C2,…,C6。从4 Hz～5 MHz,采用对数刻度进行扫频,每次测量205个点。

岩心中饱和的是0.5 mol/L的盐溶液。图1绘制了电阻率在不同饱和度、频率下的变化规律;图2为在同等条件下,岩心电容率在不同饱和度、频率下的变化规律。对比图1和图2可以发现:

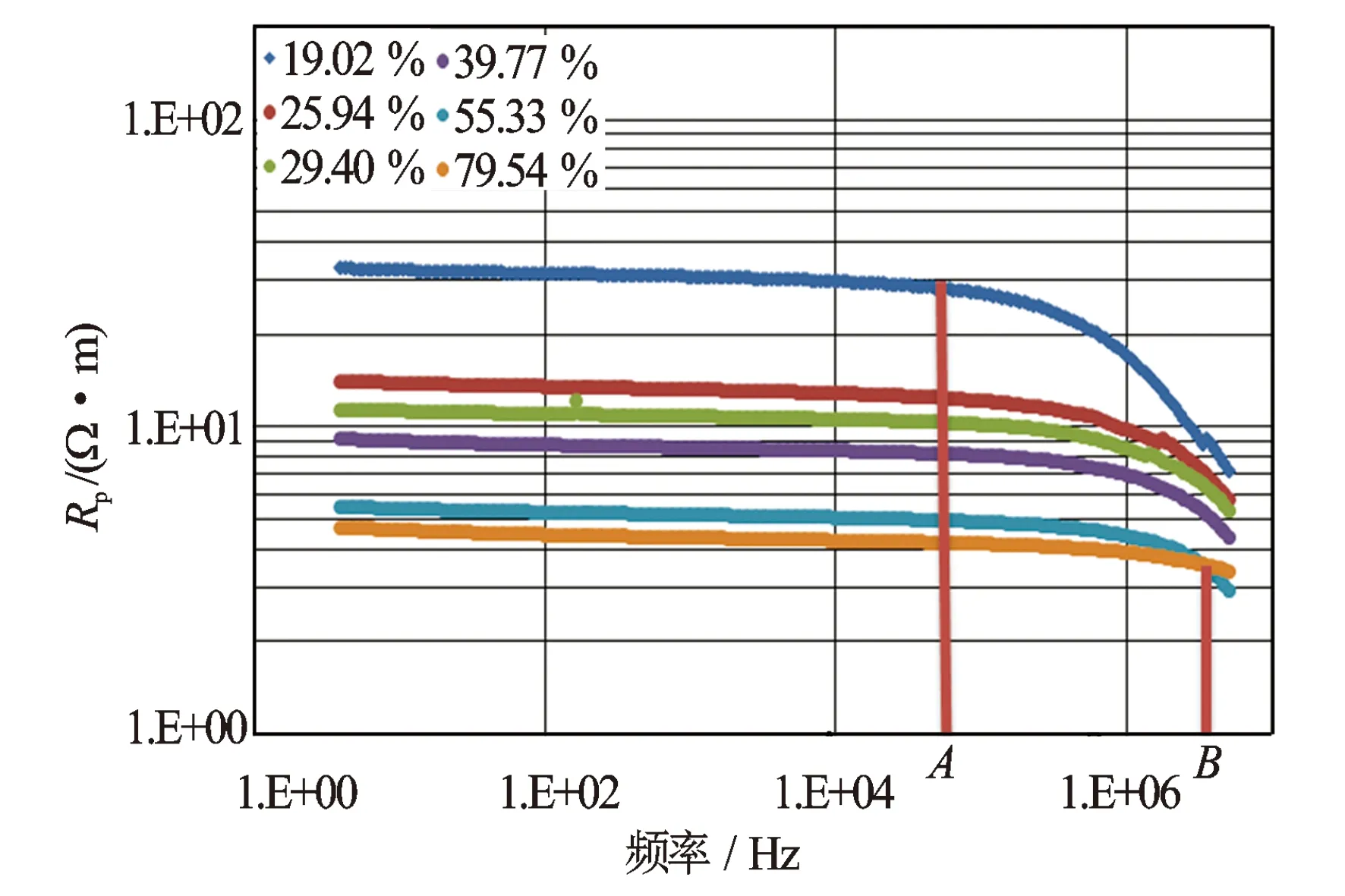
图1 13号岩心不同饱和度电阻率频散图

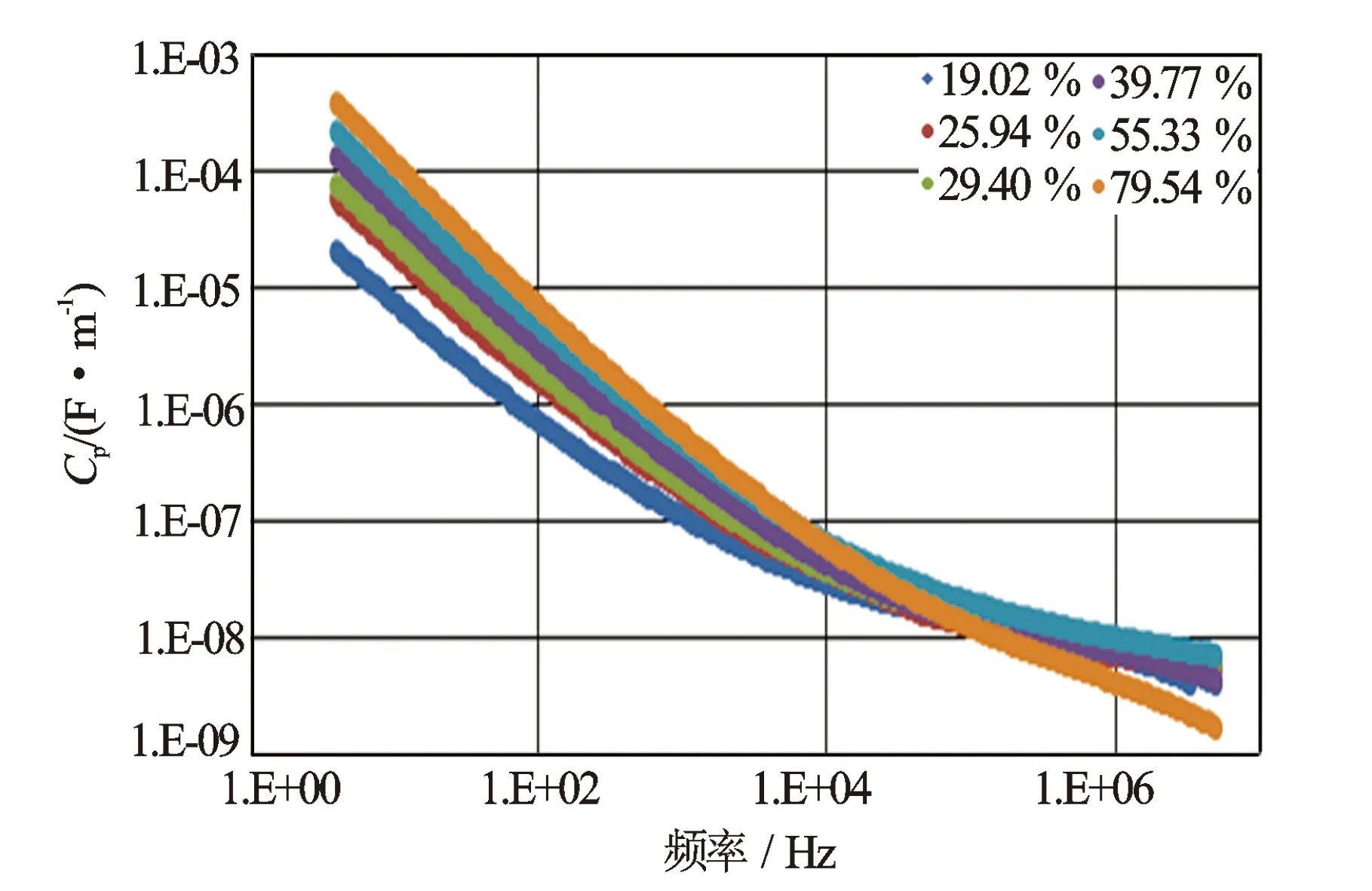
图2 13号岩心不同饱和度电容率频散图

(1) 同等条件下,电阻率随着饱和度的增加而降低,电容率随着饱和度的增加而增加。

(2) 随着频率的增加,岩心电阻率逐渐降低,低频段,电阻率变化率很小,高频时,电阻率变化率较大;饱和度越低,变化率的转折点频率越小,如图1中19.02%线的A点、79.54%线的B点。

(3) 随着频率的增加,岩心电容率逐渐降低,低频段,电容率变化率很很大,高频时,电容率变化率较小;与电阻率的变化正好相反。

(4) 同等条件下,岩心的电容率比电阻率变化要大得多。

对17号灰岩岩心重复以上步骤,测量不同频率、饱和度下电阻率和电容率参数。因为其孔隙度很小,驱替较困难,只测到4个饱和度点。17号岩心的饱和度参数见表4。

表4 17号灰岩烘干数据表

同样,对17号灰岩岩心在4 Hz～5 MHz频率范围内对每个饱和度下岩样进行了扫频测量,然后根据电极系数,将所测得电阻和电容转换为电阻率和电容率参数(见图3、图4)。

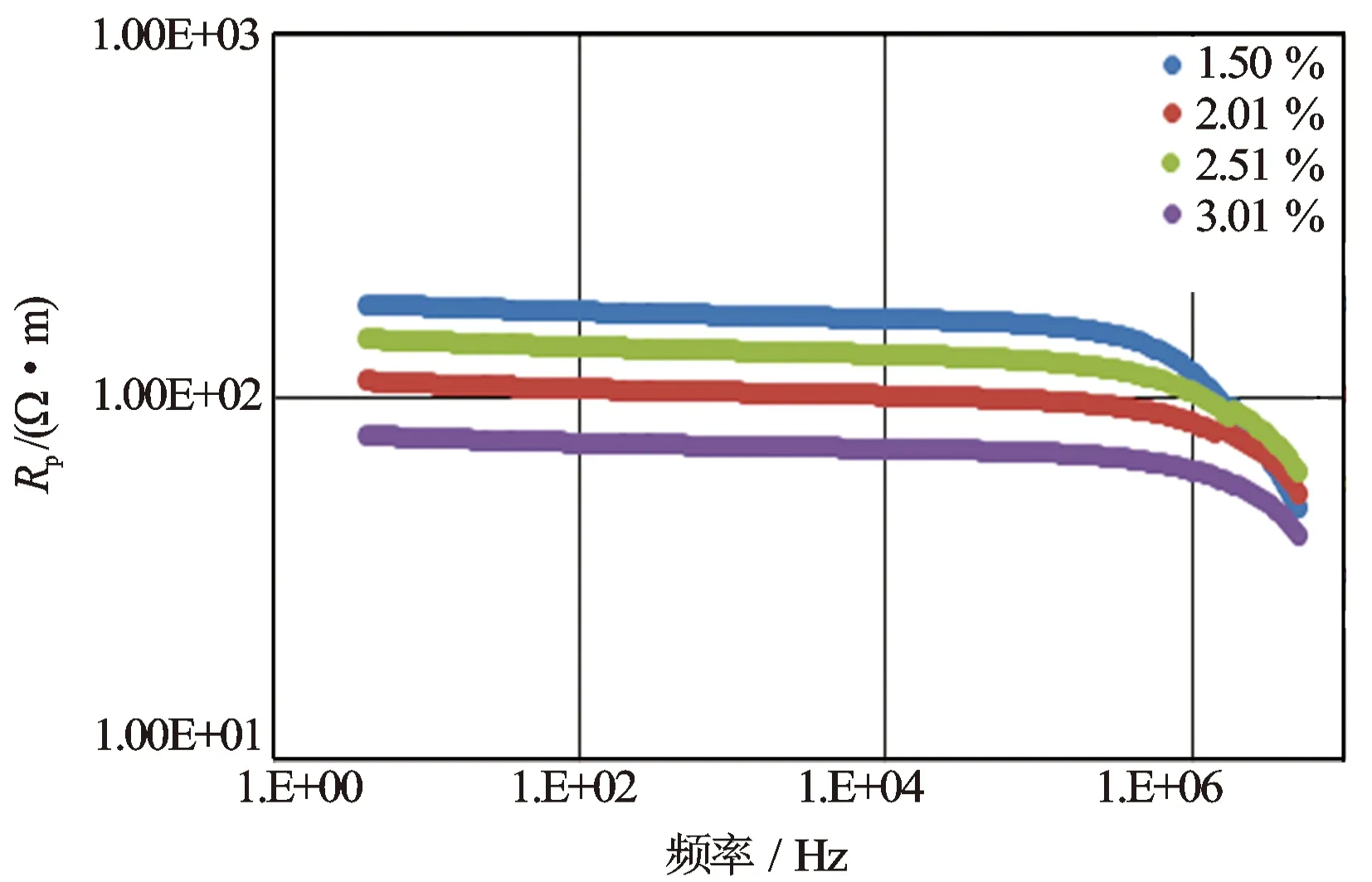
图3 17号岩心不同饱和度电阻率频散图

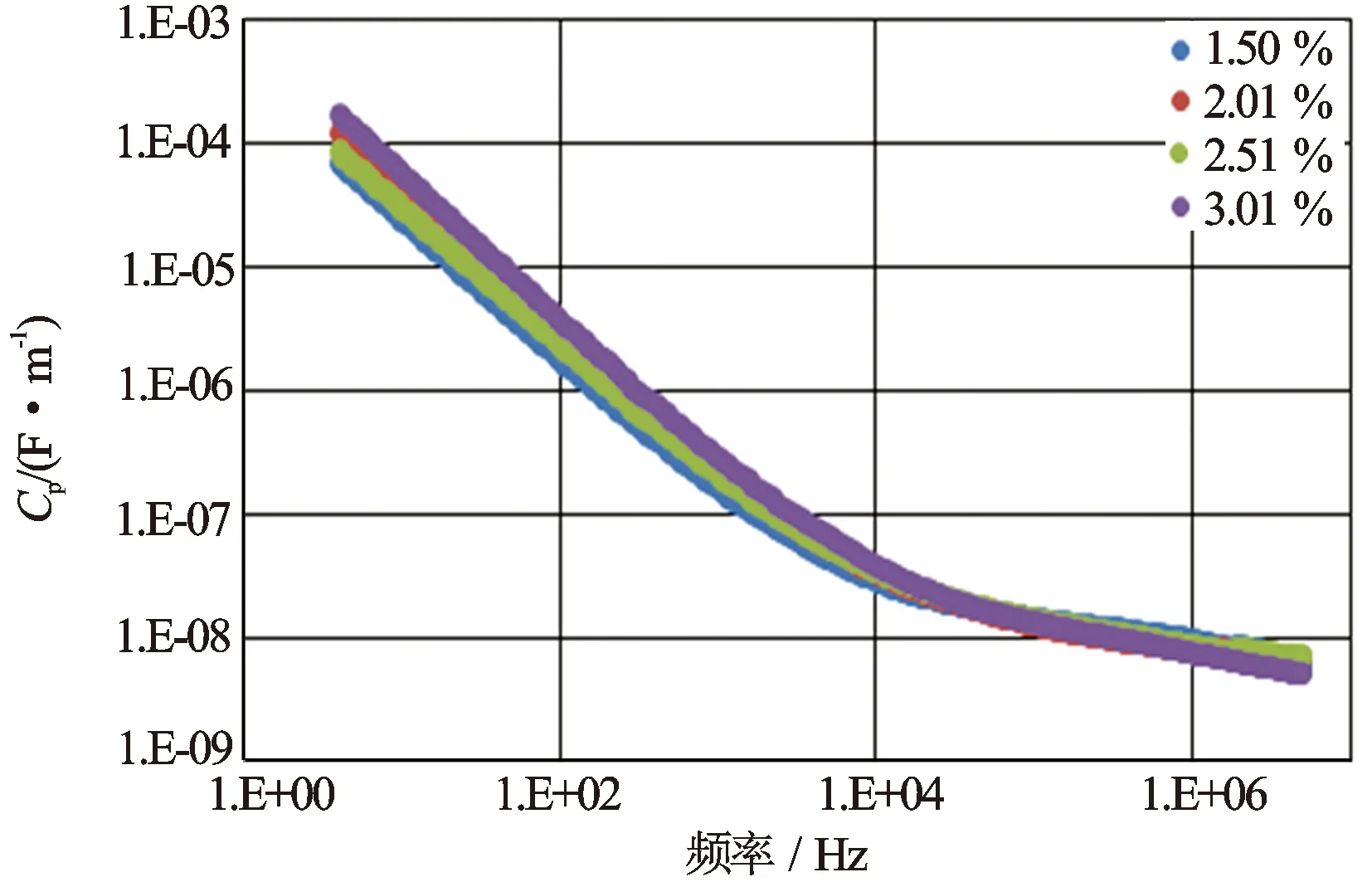
图4 17号岩心不同饱和度电容率频散图

2.2 电阻率与电容率频散度特征分析

频散度:在一定频率范围内,岩心电阻率或电容率相对于频率的变化率称为这个参数的频散度。假设频率为f1时测得电容率为C1,电阻率为R1,频率为f2时测得C2和R2,则电容率的频散DC和电阻率的频散DR,分别为

DR=R2-R1f2-f1

(1)

式中,R1、R2分别为2次测量的电阻或电阻率,Ω·m;f1、f2分别为2次测量对应的频率,Hz。

DC=C2-C1f2-f1

(2)

式中,C1、C2分别为2次测量的电容率,F/m。

实际计算时采取了以下数学处理方法。

(1) 首先对电阻率和电容率进行0～1归一化处理,其计算方法见式(3);

(2) 对频率取对数;

(3) 频散度的计算采用式(4)和式(5);

C′=C-CminCmax-Cmin

(3)

式中,C、Cmin、Cmax分别为当前电容率、测量范围内最小和最大电容率,F/m;f1、f2分别为2次测量对应的频率,Hz。对于电阻率用同样的方法,进行归一化。

则计算频散度方法

3〗2-R′1lgf2-lgf1

(4)

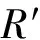
3〗2-C′1lgf2-lgf1

(5)

经过以上处理以后分析岩心的频散度变化规律。计算13号岩心电阻率的频散度。

(1) 岩心电阻率的频散度随着饱和度的增加,变化规律一致性不好,有的增大,有的减小;

(2) 岩心电容率的频散度随着饱和度的增加,变化规律一致性较好,基本上成线性增加的趋势;

(3) 同等条件下,在低频时,电容率的频散度大于电阻率的频散度,频率越低,二者之间的差异越明显,例如,测量频率24 Hz、饱和度为25.94%时,电阻率频散度为0.0752,电容率频散度为2.99,差2个数量级。同样饱和度在192 Hz时,电阻率频散度为0.006 96,电容率频散度为0.049 09,仅差1个数量级。在高频时,电阻率频散度大于电容率的频散度。

图5 13号岩心不同频率下饱和度与电阻率频散度关系

电阻率频散度与饱和度之间的关系不明确,采用相关系数法,尝试建立电阻率频散度DR与岩心饱和度之间的关系(见图5)。给出24、192 Hz与3 776 000 Hz的拟合关系式(6)～式(8),但效果并不好。

Y24=7E-05x2-0.0086x+0.2709R2=0.7823

(6)

Y192=7E-06x2-0.0009x+0.0266R2=0.8109

(7)

Y3776000=4E-09x2-6E-07x+2E-05R2=0.8794

(8)

电容率的频散度与饱和度以及频率之间具有明确的关系(见图6),其规律是频率越低,频散度越大;饱和度越高,频散度越大。

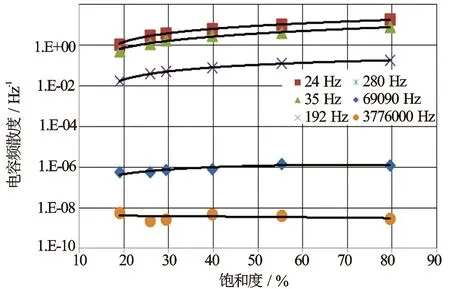
图6 13号岩心不同频率下饱和度与电容率频散度关系

通过相关性分析,给出了电容率频散度DC与饱和度之间的关系式(9)～式(14),从这些计算式来看,电容率参数的频散度计算岩心饱和度是可行的。

y24=6E-11x2+2E-08x-3E-07R2=0.9996

(9)

y35=5E-11x2+6E-09x-8E-08R2=0.9909

(10)

y192=-8E-13x2+4E-10x-5E-09R2=0.9991

(11)

y280=4E-13x2+7E-11x-7E-10R2=0.9292

(12)

y69090=-3E-17x2+5E-15x-4E-14R2=0.833

(13)

y3776000=9E-22x2-2E-18x+4E-16R2=0.0742

(14)

对灰岩岩样作了同样的频散度分析,其规律基本一致,只是灰岩的数据点较少,规律性不如砂岩明显。

2.3 现象分析

(1) 岩心的电阻率随着频率的变化,其变化率很小,即电阻率的频散度很小。

(2) 岩心的电容随着频率的变化,其变化率很大,即电容率的频散度很大,并且,频散度与岩心饱和度正相关,与测量频率负相关。

究其原因,因为电容率参数涉及到被测物体的极化,而岩石是一个多相态、空间复杂的电介质,从宏观角度,涉及到不同矿物成分的岩石颗粒、油气水不同的流体,还涉及流体存在的粒间孔、粒内孔、溶洞、裂缝等空间系统;从微观的角度,涉及到Na+/Cl-等阴阳离子、水分子、离子基团、烃类大分子等粒子,而极化的类型包括电子极化、离子极化、界面极化、转向极化等,其微观机理十分复杂。

但是,从频散图中可以看出,无论是电阻率参数,还是电容率参数,以及相应的频散度参数,样品在低频域和高频域都表现了不同的变化特征。特别是电容率在低频段,随着频率的增加其降低的速度非常快,而在高频段,降低速度变慢。

3 结 论

(1) 同等条件下,岩石电容率比电阻率参数随频率的变化更加明显。

(2) 无论是砂岩岩心还是灰岩岩心,电容率在低频段频散更明显,不同的频率段,其频散度有差异。

(3) 根据实验结果可知,岩心电容率与其饱和度参数具有较稳定的关系。

(4) 根据实验结果,建立了低频段和高频段电容率频散度与饱和度的计算关系。

参考文献:

[1] Pelton W H, Ward S H, Hallof P G, et al. Mineral Discrimination and Removal of Inductive Coupling with Multi Frequency IP [J]. Geophysics, 1978, 43(3): 588-609.

[2] Pelton W H, Smith B D, Sill W R. Interpretation of Complex Resistivity and Dielectric Data [J]. part II: Geophys Trans, 1984, 29(4): 11-45.

[3] Kuafman A A, Wightman W E. A Transmission-line Model for Electrical Logging Through Casing [J]. Geophysics, 1993, 58(12): 1739-1747.

[4] David P L, Kevin M F. Influence of Pore Fluid Chemistry on the Complex Conductivity and Induced Polarization Response of Berea Sandstones [J]. Geophysics Research, 2001, 106(B3): 909-917.

[5] Anderson B, Barber T, Lüling M, et al. Identifying Potential Gas-producing Shales from Large Dielectric Permittivities Measured by Induction Quadrature Signals [C]∥ SPWLA Annual Logging Symposium, Edinburgh, Scotland, May 25-28, 2008.

[6] Altman R, Anderson B, Rasmus J, et al. Dielectric Effects and Resistivity Dispersion on Induction and Propagation-resistivity Logs in Complex Volcanic Lithologies, a Case Study [C]∥SPLWA 49th Annual Logging Symposium, Edinburgh, Scotland, May 25-28, 2008.

[7] Anderson B, Barber T, Lüling M. Observations of Large Dielectric Effects on Induction Logs, or Can Source Rocks be Detected with Induction Measurements [C]∥SPWLA 47th Annual Logging Symposium, Veracruz, Mexico, Jun 4-7, 2006.

[8] Illfelder H M J, Badea E A, Boonen P, et al. Identification of Formation Fluids Using the Dielectric Constant Determined from LWD Propagation Measurements [C]∥SPWLA 49th Annual Logging Symposium, Edinburgh, Scotland, May 25-28, 2008.

[9] Seleznev N, Boyd A, Habashy T, et al. Dielectric Mixing Laws for Fully and Partially Saturated Carbonate Rocks [C]∥SPWLA 45th Annual Logging Symposium, Noordwijk, the Netherlands, Jun 6-9, 2004.

[10] Toumelin E, Torres-Verdin C, Bona N. Improving Petrophysical Interpretation with Wideband Electromagnetic Measurements [J]. SPE Journal, 2008, 13 (2): 205-215.

[11] Haugland M, Badea E A, Illfelder H M J. LWD Propagation Resistivity Invasion Processing Based on Dielectric-independent Resistivities or on Alternatively-parameterized Resistivities [C]∥SPWLA 47th Annual Logging Symposium, Veracruz, Mexico, Jun 4-7, 2006.

[12] Emmanuel Toumelin, Carlos Torres-Verdin. Pore-scale Simulation of Khz-ghz Electromagnetic Dispersion of Rocks: Effects of Rock Morphology, Pore Connectivity, and Electrical Double Layers [C]∥SPWLA 50th Annual Logging Symposium, June 21-24, 2009.

[13] Mehdi Hizem, Henri Budan, Benoit Deville, et al. Dielectric Dispersion: A New Wireline Petrophysical Measurement [C]∥SPE 116130, Sept 21-24, 2008, 1-21.

[14] 唐炼, 韩有信, 张守谦, 等. 大庆油田泥质砂岩介电特性实验研究 [J]. 大庆石油学院学报, 1994, 18(4): 1-5.

[15] 曾文冲, 赵文杰, 臧德福. 井间电磁成像系统应用研究 [J]. 地球物理学报, 2001, 44(3): 411-420.

[16] 魏宝君, 张庚骥. 三维井间电磁场的正反演计算 [J]. 地球物理学报, 2002, 45(5): 735-743.

[17] 魏宝君, 张庚骥, 曾文冲. 井间电磁成像的迭代反演算法 [J]. 地球物理学报, 1999, 42(5): 711-717.

[18] 陈序三, 赵文杰, 朱留方. 复电阻率测井及其应用 [J]. 测井技术, 2001, 23(5): 327-331.

[19] 高杰, 冯启宁, 孙友国. 电极型复电阻率测井方法及其应用 [J]. 石油学报, 2003, 24(1): 62-68.

[20] 王伟男, 童茂松, 陈国华, 等. 泥质砂岩的物理性质及其测井应用 [M]. 北京: 石油工业出版社, 2004.

[21] 童茂松, 郭立新. 复电阻率测井技术及其在大庆油田的应用 [J]. 勘探地球物理进展, 2007, 30(6): 259-463.

[22] 童茂松. 激发极化测井的谱采集与分析技术研究 [D]. 长春: 吉林大学, 2004.

[23] 童茂松, 丁柱. 岩石复电阻率频谱模型参数的反演 [J]. 测井技术, 2006, 30(4): 303-305.

[24] 柯式镇, 冯启宁, 孙艳茹. 岩石复电阻率频散模型及其参数的获取方法 [J]. 测井技术, 1999, 23(6): 416-418.

[25] 柯式镇, 何亿成, 邓友明, 等. 复电阻率测井响应的数值模拟 [J]. 测井技术, 2002, 26(6): 446-448.

[26] 柯式镇, 刘迪军, 冯启宁. 线圈法岩心复电阻率扫频测量系统研究 [J]. 勘探地球物理进展, 2003, 26(4): 309-312, 328.