三参数Weibull分布下基于BRM的LED照明灯寿命预测
张建平,陈文龙,陈 晓,应开雄,成国梁,邱迎吉,金蓓雯
(1.上海电力学院 能源与机械工程学院,上海 200090;2.上海天逸电器股份有限公司,上海 201611;3.浙江京东方显示技术有限公司,浙江 绍兴 312000)
1 引 言
发光二极管(LED)作为一种新型高效的固体光源,与传统白炽灯和荧光灯相比,具有体积小、寿命长、无毒、高亮度、不易破碎、低能耗、可回收再利用和响应速度快等优点[1-2],已广泛应用于显示屏、背光源、汽车照明、指示信号灯和景观照明等各种领域,被誉为最具发展潜力的第四代照明光源。随着半导体技术的不断发展,市场上LED照明灯在正常使用条件下的寿命均高达数万小时[3],而目前关于LED照明灯寿命预测方法的国家标准还不明确。为了节省LED照明灯寿命试验时间,降低寿命预测成本,弄清失效机理,迫切需要对其开展加速寿命预测的研究,以期在短时间内掌握产品的寿命信息。
目前,国内外学者关于测试LED等光电类产品的寿命,主要采用温度加速应力试验或电流加速应力试验两种方法[4]。笔者对有机发光二极管(OLED)利用对数正态分布和最小二乘法(LSM)完成了寿命预测[5]。Yazdan Mehr等[6]和 Wang等[7]基于亮度指数衰减模型预测了LED灯珠的寿命。董懿[8]通过三组恒定温度应力加速寿命试验得到了LED照明灯的寿命信息,但在寿命推算方面,得到的特征寿命误差较大。
针对文献[8]预测LED照明灯寿命精度不高的问题,本文利用三参数Weibull分布和双线性回归法(Bilinear Regression Method,BRM)相结合的方法完成了加速寿命试验数据的统计分析,这种方法的优点在于寿命计算精度高且简单易行,是一种快速高效得到LED照明灯寿命信息的方法。
2 寿命预测理论模型
2.1 寿命预测流程
对于光电类产品,加速寿命预测的基本思想是运用较高应力水平下的寿命信息来推导正常应力水平下的寿命特征,其基本方法是根据加速寿命试验数据选取合适的寿命分布函数和加速寿命模型,再采用合理的寿命参数估计方法完成试验数据的统计分析,从而得到产品的寿命信息。
对于LED照明灯,这里采用三参数 Weibull分布函数、BRM以及Arrhenius加速模型来精确预测其寿命,寿命预测基本流程如图1所示。

图1 LED照明灯寿命预测流程Fig.1 Flowchart of life prediction for LED lamps
2.2 寿命分布函数
Weibull分布在可靠性工程中被广泛应用,尤其适用于产品累计失效的分布形式,在各种寿命试验的数据处理方面,它具有较好数据拟合效果[9]。为获得LED照明灯的寿命信息,先假设其寿命服从三参数 Weibull分布,则有[10]:

式中:m、η、t0分别为形状参数、尺度参数和位置参数。实际上,Weibull三参数在计算LED照明灯的寿命中起关键作用。
2.3 寿命参数估计
线性回归是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析方法,在统计学中应用十分广泛,单一回归性方法误差较大,而双线性回归法极大地提高了计算的精度。因此,这里基于BRM来计算Weibull函数的3个参数。
将式(1)进行变形,可以得到以下两种形式的线性函数式:
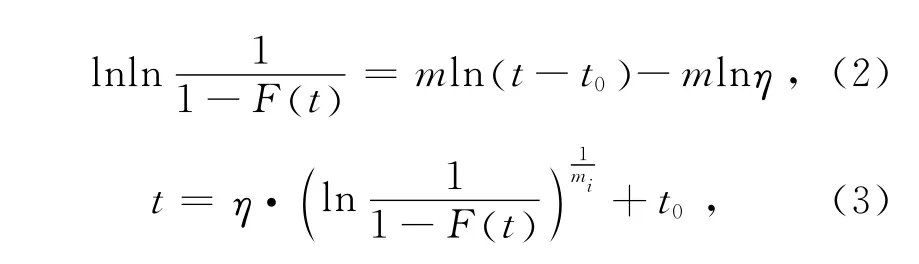
上式均可简写为:
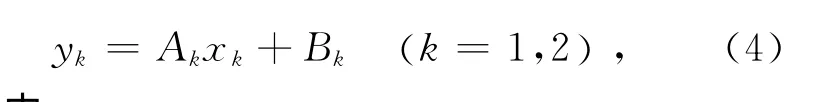
其中:

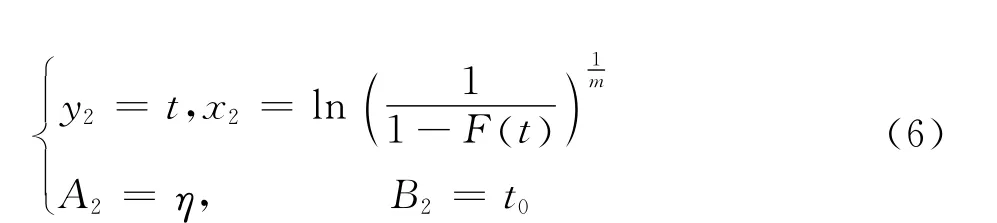
对于线性回归方程

由LSM公式可得到:

由式(5)及(7)可得形状参数m为:

再结合A1=m可得到尺度参数η表达式为:

由式(6)及(7)可得到位置参数:
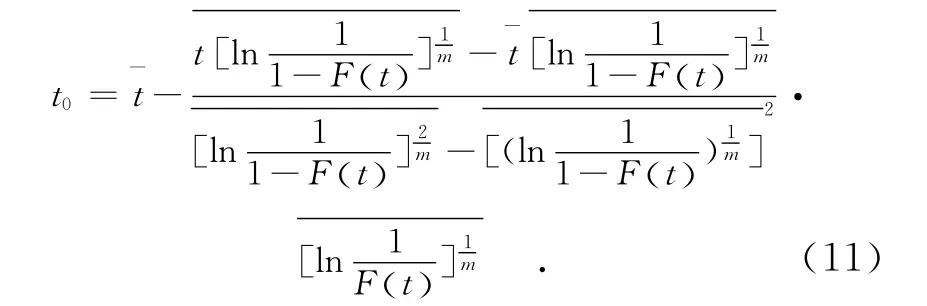
事实上,式(9)、(10)及(11)分别是关于 m、η以及t0的计算公式,可以记为一般函数,即有:

由式(12)可知,m与t0是相互迭代的算式,可通过迭代的方式求解参数m、η以及t0,具体迭代流程图如图2所示。
2.4 拟合精度衡量
为了衡量曲线拟合的精度,即拟合值与真实值之间的偏差程度,通常采用残差平方和Q作为统计分析指标。Q即为所有观测点距回归直线的残余误差的平方和。它是在排除掉因试验误差、x对y的非线性影响以及其他未加控制因素的影响情况下,得到x对y的变差,用于考虑x与y之间的线性关系。Q可用式(13)表示:

残余标准差ε是回归方程的精度参数,估计出y的随机波动量,其值愈小,回归方程的准确度

图2 基于三参数Weibull函数的BRM迭代流程图Fig.2 BRM iterative flowchart based on threeparameter Weibull function
愈高,ε可写为:

式中:N为样本个数。
3 试验数据
在LED照明灯寿命预测研究中,文献[8]在保证加速效果达到最大而且失效机理不变的情形下,以温度为加速应力开展了3组恒定应力T1=333.15K、T2=353.15K、T3=378.15K的加速寿命试验,样品数均为n1=n2=n3=10,在光通量衰减到初始值70%作为失效标准情形下的样品失效时间列于表1。

表1 三组恒定应力试验下样品的失效时间[8]Tab.1 Sample failure time of three groups of constant-stress tests[8]
4 统计与分析
为提高LED照明灯寿命预测的计算精度和效率,这里采用自行开发的寿命预测软件来完成对试验数据的计算与分析。
4.1 加速寿命方程的确定
在采用三参数Weibull函数描述LED照明灯寿命试验数据分布基础上,基于BRM对表1中的数据进行处理,求得各恒定温度应力下的形状参数、尺度参数及位置参数,列于表2。

表2 不同加速应力下的Weibull参数Tab.2 Weibull parameters under different accelerated stresses
假设LED照明灯加速模型符合Arrhenius方程,则其特征寿命Te-1与温度应力T满足以下关系[11]:
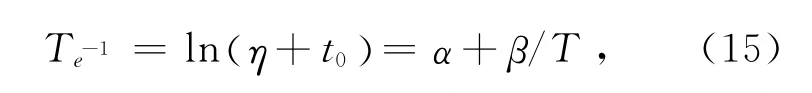
式中:α和β为加速参数,对寿命预测结果的影响较大。
文献[8]先将3组 Weibull函数的参数代入加速寿命方程中进行求解,再把3组加速参数的均值作为α和β解,为减小误差,这里采用LSM进行计算,可得:α=-4.927 8,β=4 750.186 5。因此,式(15)可重写为:
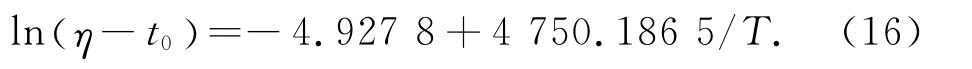
实际上,式(16)表征了LED照明灯在各温度应力水平下的加速寿命方程,即为寿命特征图,如图2所示。拟合曲线决定系数R2=0.992 6,非常接近1,证明了LED照明灯的加速模型完全符合Arrhenius方程的假定,且说明拟合程度很好。

图3 寿命特征图Fig.3 Life characteristic pattern
4.2 寿命分布模型的K-S检验
由于每组试验样本容量较小,均为10个,故在K-S检验时选取较大的显著性水平,这里取α=0.2。对3组应力下试验样品的失效时间进行检验,计算得到的 K-S统计量为:D1n,2,3={0.1067,0.1004,0 . 1220} < D0.2,10= 0.3226。因此说明了每组加速应力水平下的失效时间均通过了K-S检验,从而证明了LED照明灯寿命服从三参数Weibull分布假设的成立。
4.3 回归方程的显著性检验
为了说明三参数Weibull分布下基于BRM的LED照明灯寿命预测结果的精确性,将由式(16)计算出残余标准差ε(N=10)与文献[8]的残余标准差进行对比,其结果列于表3。
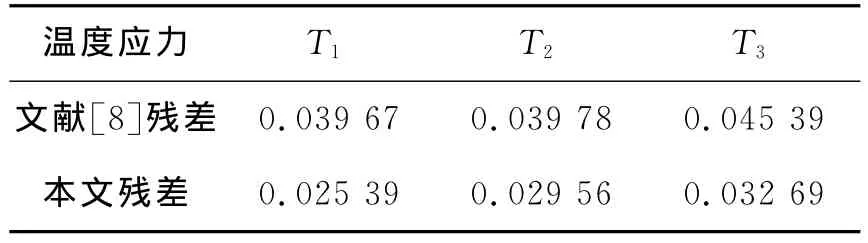
表3 残余标准差的对比Tab.3 Comparison of residual standard deviation
从表3不难看出,本文三组应力条件下的残余标准差均比文献[8]的小,由此可说明本文数据处理与计算的方法更为准确,使预测出的LED照明灯在正常工作条件下的寿命更接近真实值。
4.4 寿命的计算与对比
三参数Weibull分布下,LED照明灯在正常温度应力下的平均寿命计算公式为:
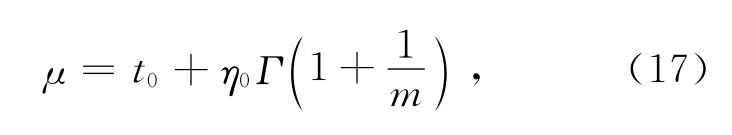
式中:Γ(·)为伽马函数,η0和m分别为正常温度应力下的尺度参数和形状参数。
将正常温度应力T0=298.15K代入式(16),可得正常工作条件下的尺度参数η0=46218.283 3。在各温度应力水平下LED照明灯的失效机理不变,即形状参数m不变,可通过各加速应力下的形状参数取加权平均来获得,则有:
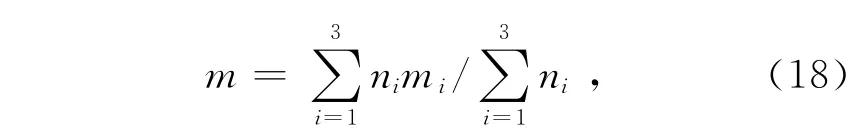
将表2中的mi(i=1,2,3)以及每组加速应力下的试验样品数量代入式(18),可得到m=2.6323。在工程应用中,通常将实际使用中的最小寿命作为位置参数t0,对表2中3组温度应力和位置参数数据点进行数据拟合,可得LED照明灯正常工作条件下位置参数t0=12934.7h。因此,结合式(15)和(17)便可得其特征寿命Te-1 =60140.4h,平均寿命μ=54879.1h。
将本文和文献[8]计算的特征寿命均与国际上最权威的ALTA9加速寿命数据分析软件(试用版)所得出的寿命(Weibull分布下)进行比较,结果见表4。可以看出,文中所算出的特征寿命相对误差仅为3.21%,而文献[8]的误差比本文高出10倍以上,这进一步说明了本文预测LED照明灯寿命的精度较高。

表4 寿命比较Tab.4 Life comparison
5 结 论
通过三参数Weibull分布下基于BRM对3组恒定应力加速寿命试验数据的统计与分析,可得出以下结论:
(1)各组温度应力下的寿命试验数据均通过了K-S检验理论,证实了三参数 Weibull分布函数适用于描述LED照明灯的寿命分布。
(2)经残余标准差的对比与分析以及寿命结果的比较,说明了基于三参数 Weibull分布下的BRM寿命预测方法得出的LED照明灯寿命精度较高。
(3)加速寿命曲线的决定系数非常接近1,证明了LED照明灯的加速模型完全符合Arrhenius方程。
(4)精确得到的LED照明灯的寿命信息,为LED照明灯的生产厂商和用户有较好的参考价值。
[1] 李相国,姚晓魁,赵广河.一种基于模拟PWM的全彩色LED显示屏[J].液晶与显示,2014,29(3):361-369.Li X G,Yao X K,Zhao G H.Full-color LED display by simulation of PWM [J].Chinese Journal of Liquid Crystals and Displays,2014,29(3):361-369.(in Chinese)
[2] Wu F T,Huang Q L.A precise model of LED lighting and its application in uniform illumination system [J].Optoelectronics Letters,2011,7(5):334-336.
[3] 高伟.AlGaInP LED转移衬底和可靠性的研究[D].北京:北京工业大学,2011.Gao W.Study of substrate transfer and reliability of alGaInP LED [D].Beijing:Beijing University of Technology,2011.(in Chinese)
[4] 李德高,王万良,闵芳胜,等.大功率LED寿命的理想因子表征[J].液晶与显示,2008,23(6):722-725.Li D G,Wang W L,Min F S,et al.Relation between ideal factor and lifetime[J].Chinese Journal of Liquid Crystals and Displays,2008,23(6):722-725.(in Chinese)
[5] Zhang J P,Liu F,Wu H L,et al.Life prediction for white OLED based on LSM under lognormal distribution[J].Solid-State Electronics,2012,75:102-106.
[6] Yazdanmehr M,Van Driel W D,Jansen K M B,et al.Lifetime assessment of bisphenol-apolycarbonate(BPA-PC)plastic lens,used in LED-based products[J].Microelectronics Reliability.2014,54(1):138-142.
[7] Wang F K,Chu T P.Lifetime predictions of LED-based light bars by accelerated degradation test[J].Microelectronics Reliability,2012,52(7):1332-1336.
[8] 董懿.照明LED模块使用寿命快速检测方法的研究[D].杭州:中国计量学院,2012.Dong Y.Research on Rapid detection technology for the life of light-emitting-diode lamps[D].Hangzhou:China Jiliang University,2012.(in Chinese)
[9] Fan J J,Yung K C,Pecht M.Lifetime estimation of high-power white LED using degradation-data-driven method[J].IEEE Transactions on Device and Materials Reliability,2012,12(2):470-477.
[10] 张建平,成国梁,周廷君,等.基于BRM下白光OLED恒定与步进应力加速寿命试验研究[J].液晶与显示,2012,27(2):187-192.Zhang J P,Cheng G L,Zhou T J,et al.Constant-step stress accelerated life tests of white OLED by BRM [J].Chinese Journal of Liquid Crystals and Displays,2012,27(2):187-192.(in Chinese)
[11] 茆诗松.加速寿命试验的加速模型[J].质量与可靠性,2003(2):15-17.Mao S S.The accelerated model of accelerated life test[J].Quality and Reliability,2003(2):15-17.(in Chinese)

