关于空气污染治理成本分配的博弈研究
◎文/卫永红 孙 策
关于空气污染治理成本分配的博弈研究
◎文/卫永红 孙 策
空气污染已经成为当前无法逃避的问题,需要各地区的联合协作,而在区域合作治理中,成本如何分配是影响合作成功与否的关键,本文依据合作博弈中的Shapley模型,提出合作治理污染的成本分配方案,并建议中央政府在此基础上发放治理补贴。
空气污染;合作博弈;Shapley模型;京津冀
北京曾在2014年APEC期间实现短暂的蓝天白云,虽然会议结束之后空气污染依旧,但是仍让我们看到了空气污染治理的希望,习总书记也发出了让“APEC蓝”留住的号召,可以说这为空气污染治理打好了上层基础。但“APEC蓝”的实现是靠中央政府颁布的强制条例,其中包括各地工厂与企业停工停产,汽车限行,北京地区甚至对所有公务人员放假7天,其成本巨大,也非长久之计。治理空气污染真正需要的是优化产业结构、社会能源结构等,这是一个长期的工程,离不开各地区的长期配合。而我们知道环境治理具有很强的外部性,作为理性人的各个地方政府都趋向于搭便车而非参与治理,各地方政府之间的博弈容易陷入囚徒困境。

表1 地方政府污染治理博弈矩阵
如表1所示,假设有A、B两省面临空气污染的状况,他们都有参与治理或者不参与两种选择,括号内数据则是他们做出选择后面临的各自收益,很明显A、B两省的占优策略均为不参与,但此时的总收益是最低的。而共同参与治理虽然总收益最高,却并非两省的选择,那么如何让没有行政隶属关系的地方政府展开协作,走出囚徒困境,正是中央需要解决的问题。我们假定参与治理的合作成本为c,而获得的收益为π,当合作时的c>π时,合作当然无法完成,这时就需要中央政府给予一定的资金补助s使得c<π+s,本文要讨论的正是在区域协作治理空气的基础上,治理成本c以及中央补助s应该如何在区域之间分配才能保证区域合作可以公平公正的进行。
关于这个问题本文用了合作博弈理论中的Shapley模型进行分析,该模型是由诺贝尔经济学奖得主LloydS.Shapley提出的,被用来解决联盟合作对策的问题。在Shapley模型中按照每个参与人对他所参与的所有联盟的边际贡献平均值作为其应得的收益或应该承担的成本,是基于各个参与人在经济效益产生或成本减少过程中的重要程度来进行分配的,这样既可以提高效率,又保证了公平合理。
一、Shapley模型简介
Shapley模型是合作博弈中最重要的解概念。合作博弈与非合作博弈很大的不同之处就是合作博弈没有一个统一的解的概念,人们很难从解集中选取一个即有效率又不失公平的解,而Shapley值就是这样一个能够解决这些问题的解。它以联盟中每个参与人的边际贡献平均值作为其应得的收益或应该承担的成本,是基于各个参与人在经济效益产生或成本减少过程中的重要程度来进行分配的,因此它是公平的,也因此在政治、经济、数学等领域得到了广泛应用,尤其在计算产业链合作的收益分配中起到了很大的作用。
Shapley从有效性公理、对称性公理、和可加性公理出发,提出合作对策解的概念。依据本文的研究目的,在这里作者只从成本分摊的角度介绍模型,对收益的分摊经过相应的简单变型即可得到,因此在这里不再赘述。
成本分配中的合作博弈定义是以特征函数(N,C)的形式给出的。假设集合N={1,2,…,n},n为集合中参与人的个数。设S是N的子集,用来表示N集合中部分参与人所组成的一个集合。C是每个组合相对应的特征函数,C(S)是S子集的成本值,相应的,C(N)表示全部参与人都在内的集合的总成本值,C(i)表示第i个人独立完成全部工作时的成本值,Xi表示的是成员i在合作中所承担的成本值。根据之前一些学者的研究,我们可以归纳出以下几点沙普利模型需满足的条件:
①C(S)+C(T)≥C(S∪T),∀S,T⊂N,S∩T=Φ;即由两个联盟所组成的新联盟,其合作成本不大于原来两个联盟的成本之和。否则合作不成立。这是合作得以成立的必要条件之一。
②C(i)≥Xi,∀⊂N;即成员i在合作联盟中所承担的成本不大于其单干时成本,体现了个人理性。
③∑i∈NXi=C(N),∀i∈N;即总成本应在n个参与人之间完全分配。
④∑i∈SXi≤C(S),∀S∈N;即某一联盟内的个体单独工作的成本之和应不大于组成的这一联盟的成本值,体现了合作联盟的集体理性
满足以上几个条件的成本分配方案的解被认为在合作博弈中是稳定的,而Shapley模型符合以上条件。在模型中,计算出参与人i承担的成本等于该参与人对所参加的每个联盟的边际贡献的平均值。用φi(C)表示成员i在大联盟中所承担的成本,其结果由以下公式求得:
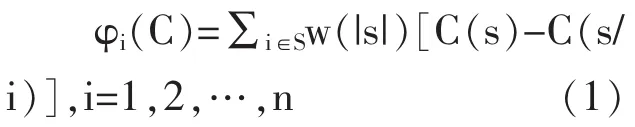

|s|表示的是联盟中成员的个数,C(S)表示联盟S的成本,C(s/ i)表示联盟中除去成员i后的成本,w(|s|)是成本的加权项,C(s)-C(s/i)表示成员i在包含i的联盟S中的边际贡献,即边际成本。对于w(|s|)是从概率角度分析的,对集合N来说,每个参与人在不同的位置就是一个不同的排列,如(i1,i2,…,in)是一种序列,倒过来(in,in-1,…,i1)又是一个序列,n个成员就有n!种排序,S为某个包含成员i的集合,令第i个成员排在第|s|个位置,(|s|-1)!就表示排在该成员前面的所有成员的全排列,(n-|s|)!表示排在该成员后面的全排列,w(|s|)即为成员i出现在这个位置的概率。
φi(C)本质就是i在每个联盟s的边际成本的期望值。
二、Shapley模型在合作治理空气污染中的应用
我们假设一个例子来说明Shapley模型在空气污染成本分配中的应用。假设对空气污染的治理需要三个区域的协作完成,这三个区域分别为X、Y、Z省,三个区域按照其污染治理成本的大小依次分为高中低三个层次且cX=1000亿、cY=800亿、cZ=600亿,总成本为 C1=800+600+1000= 2400亿;如果两两省份联盟进行雾霾治理,其成本依次为 cXY= 1600亿、cXZ=1300亿、cYZ=1200亿;当三个省份组成大联盟进行治理时的成本为cXYZ=2000亿。详情如表2。

表2 省份联合成本(亿元)
显然通过上述计算分析,采用三省份联合方式来治理雾霾可以达到治理成本最低的目的,如果此时仍按照各省份单独治理时的成本所占比例来分配中央政府的补助显然是不合理的,而应该按照三省联合时各省份所承担的成本比例来分配补助更为公平,我们可以通过合作博弈并利用Shapley值的计算来解决这个问题,先计算出2000亿的成本中三省份各自承担的份额,即可按照份额比例来计算出补助的分配方式。
将上述分析用公式表示:
N={X,Y,Z},C (X)=1000,C(Y)=800,C(Z)=600,C (X,Y)= 1600,C (X,Z)=1300,C (Y,Z)= 1200,C(X,Y,Z)=2000。关于联盟中X省份承担的治理成本φi(V)计算如表3所示,其中X参与的集合包括X,X∪Y,X∪Z,X∪Y∪Z。
在表3中,C(S)为集合s所产生的成本;C(s/i)为除去省份i的省份集s所产生的成本;C(s)-C(s/i)为省份i对集合s的边际贡献。将w(|s|)[C(s)-C(s/i)]的各值相加,就是省份i对包含它的所有省份集合的边际贡献的均值。可得φx(C)=850。同理φY(C)、φZ(C)计算如表4与表5所示。φY(C)=700,φZ(C)=450。

表3 X省份成本(亿元)
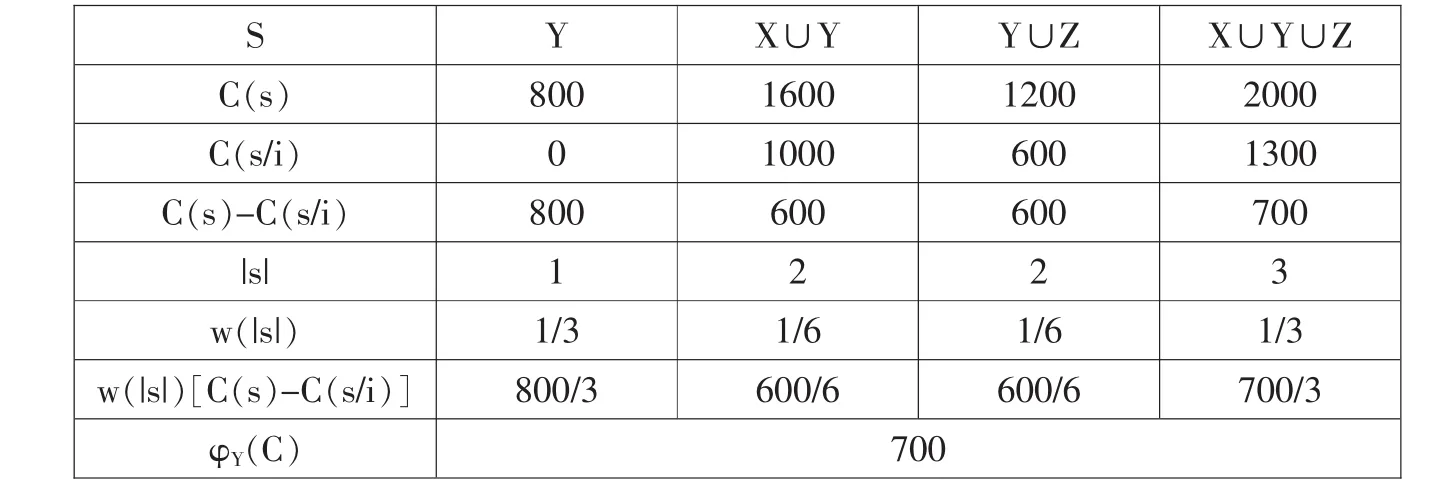
表4 b省份成本(亿元)

表5 c省份成本(亿元)
根据以上分析可以验证,φX(C)、φY(C)、φZ(C)的数值满足沙普利模型的四个条件。按照此方法,X、Y、Z三省在合作后所承担的成本,比单独治理时的成本要低,且依次承担 42.5%、35%、22.5%的空气污染治理成本。相比原来的41.47%、33.33%、25%有所改变,这样的结果更为合理,在保证总成本降低的基础上兼顾了公平,那么按照计算出的这个比例来分配中央政府的补贴,也更加合理。
三、结论
通过分析,本文提出了区域合作成本按照Shapley模型进行分配、国家按比例调节补贴的战略,这样既兼顾了公平,又有利于监管。
空气污染问题不是一朝一夕可以得到解决,因此制定一个切实可行、稳定有效的长期战略显得尤为重要。合作博弈的理论就为区域合作打好了一定的理论基础。当前中国的空气污染问题中,京津冀区域最为严重,也最受关注,天津市作为其中一员,在合作治理空气污染的进程中担任重要角色,在京津冀一体化的战略里,天津应发挥其区位优势、科技优势、创新优势,积极承担其责任,为国家经济发展和生态保护贡献自己的力量。
[1]中华人民共和国环境保护部,数据中心.http://www.zhb.gov.cn/.
[2]施锡铨.合作博弈引论[M].北京:北京大学出版社,2012:65-94.
[3]吴博.雾霾协同治理的府际合作研究——以“京津冀”及“珠三角”为例[D]湖北:华中师范大学硕士论文.
[4]马士华,王鹏.基于Shapley值法的供应链合作伙伴间收益分配机制[J].工业工程与管理2006,(4):43-49.
责任编辑:张丽恒
F224.32
A
1006-1255-(2015)04-0034-03
卫永红(1990—),天津财经大学理工学院。邮编:300202
孙 策(1991—),天津财经大学理工学院。邮编:300202

