基于瞬时故障特征频率趋势线和故障特征阶比模板的变转速滚动轴承故障诊断
王天杨, 李建勇, 程卫东
(1.清华大学机械工程系,北京 100084;2.北京交通大学机械与电子控制工程学院, 北京 100044)
基于瞬时故障特征频率趋势线和故障特征阶比模板的变转速滚动轴承故障诊断
王天杨1, 李建勇2, 程卫东2
(1.清华大学机械工程系,北京 100084;2.北京交通大学机械与电子控制工程学院, 北京 100044)
针对难以从滚动轴承的时频分布中提取瞬时转频分量的问题,本文利用由轴承包络时频谱中提取的瞬时故障特征频率替代传统瞬时转频实现重采样,进而基于故障特征因子与转频阶比边带构造故障特征阶比模板以实现变转速运行模式下滚动轴承故障诊断。其具体算法由以下四个部分组成:首先,联合应用谱峭度滤波算法与短时傅里叶变换得到能够突出瞬时故障特征频率的包络时频谱;其次,提出基于幅值重调的峰值搜索算法对瞬时故障特征趋势线进行提取;再次,以瞬时故障特征频率趋势线为基础对原信号进行故障相角域重采样并得到故障特征阶比谱;最后,根据被监测轴承的故障特征因子构造故障特征阶比模板对滚动轴承的运行状态与故障类别进行判断。仿真算例和应用实例证明了该算法的有效性。
故障诊断;滚动轴承; 故障相角域; 故障特征阶比谱; 转频阶比边带
引 言
若滚动轴承存在故障,故障点与其配合部件之间将因碰撞产生的短时、快速衰减冲击并激励其他部件产生高频共振。如果转速恒定,该类冲击将以等间隔形式出现,相应的重复频率则为故障特征频率。该故障特征频率通常会被共振高频所调制,共振解调技术[1]即利用该特性实现对滚动轴承的故障诊断。但在工程实际中,滚动轴承并非均以匀转速运行,例如:设备的启停阶段,风力发电机、直升机螺旋桨、矿用电铲等。在变转速下,由故障引起的冲击将不再以周期形式出现。这将导致以共振解调为代表的以转速恒定为前提条件的传统轴承故障诊断方法失效[2]。
实际上,对变转速运行设备中的滚动轴承进行故障诊断已成为领域内的热点之一[3-5]。阶比分析技术[6]则是其中应用最广且效果最好的。其算法本质是以等角间隔对时域非平稳信号进行重采样,再将其转化为角域平稳信号的同时恢复传统故障诊断算法的功效;其成功的关键在于对设备即时转速的获取。根据即时转速获取方法的不同,可将阶比跟踪算法分为两类:第一类是利用辅助设备获取转速信息[7-9];第二类则是根据信号本身对转速进行估计[10]。第一类算法首先利用转速计测得的即时转速信息并对变转速滚动轴承振动信号进行角域重采样;其次结合希尔伯特变换和快速傅立叶变换求得相应的阶比包络谱;最后,利用阶比包络谱对滚动轴承的运行状态及故障位置进行判别。该算法虽然能实现变转速滚动轴承的故障诊断,但对转速辅助设备的依赖也将制约该类算法的广泛使用[11]。
第二类算法仅依靠振动信号本身即可对瞬时转频进行估计:Urbanek J等[12]利用齿轮信号时频分析中突出的啮合频率成分间接地对其转速进行估计,进而解决齿轮的故障诊断问题;赵晓平等[13]则提出短时傅里叶变换与Viterbi拟合算法相结合的算法对涡轮离心机升速阶段振动信号的瞬时频率进行估计。但是,滚动轴承的时频分析结果中却缺乏与其转频直接相关的、突出的、可直接提取的时频分量,这将给应用该类算法解决变转速模式下的滚动轴承故障诊断问题提出挑战:首先,在滚动轴承振动信号的时频表达中,转频对应的时频成分往往因其幅值小于由故障引起的高频共振成分而难以被提取;其次,与转频相关的趋势成分往往也因幅值较小而并不连贯;最后,即使能够解决上述问题,从时频图中提取到的趋势分量也极有可能是与转频成分同步但比例未知的倍频成分。而此未知比例关系将使相应的重采样结果及其包络谱失去明确的物理意义,并影响最终的故障诊断。
针对上述问题,本文提出利用包络时频谱,而不是时频谱对滚动轴承的瞬时故障特征频率而不是瞬时频率进行提取。为解决瞬时故障特征频率给传统重采样结果带来的影响,本文利用被监测轴承的故障特征因子与转频阶比边带构造故障特征阶比模板实现最终的故障诊断。
1 算法部分
为解决难以从滚动轴承时频分析中获取转频分量的问题,本文提出了利用瞬时故障特征频率(Instantaneous Fault Characteristic Feature, IFCF)替代传统转频的解决策略。下式为内圈、外圈或滚动体存在故障时的故障特征频率:
(1)
(2)
(3)
式中n为滚动体数;fr为轴承所在轴的转频;d为钢球直径;D为滚道节径;φ为接触角。可以看出,除转频外决定轴承故障特征频率的其他参数均为被监测轴承的几何参数。实际上,若轴承存在故障,其故障特征频率和转频的比例关系固定且仅与轴承几何参数相关。本文将此比例系数称为故障特征因子(Fault Characteristic Coefficient,FCC):
FCCo=fo/fr
(4)
FCCi=fi/fr
(5)
FCCb=fb/fr
(6)
因此,若滚动轴承的转速随时间变化,其故障特征频率将随着转频同步变化且比例关系保持不变。该特性将使轴承的故障特征频率成为能够替代转频的等效参量。然而,能否实际应用还取决于其可提取性。一般的,若故障轴承以匀转速运行,其包络谱中的故障特征频率及其倍频处会出现明显的峰值。若能确定由故障引起的共振高频并构造带通滤波对其进行提取,响应包络谱中的故障特征频率峰值将更为突出。这将使故障特征频率在与轴承转频同步变化的同时也将具备可提取性。
本文将故障特征频率随时间的变化形成的趋势称为IFCF趋势线,并以其作为起点提出一套适合变转速滚动轴承故障诊断策略:
第1步 联合应用谱峭度滤波与短时傅里叶变换(STFT)获得包络时频谱。
作为峭度的延伸概念,谱峭度能够衡量冲击性在频域中的分布,其表达式为
(7)
式中 符号|·|和<·>分别表示取模和时域平均(取均值),X(t,f)为分析信号x(t)在频率f处得到复包络。本文选择文献[14]提出的基于Krtogram的快速算法自适应地确定轴承共振频带对应滤波中心、宽及尺度参数。并利用STFT计算滤波结果的包络时频谱。由于基于谱峭度滤波能够最大程度地凸显轴承的故障特征,对应的包络时频谱中应该包含清晰且突出的IFCF趋势线。
第2步 利用基于幅值重调的峰值搜索算法从包络时频谱中提取IFCF趋势线。
理论上,在谱峭度滤波后的包络时频谱中,瞬时故障特征频率在每个时刻对应的瞬时包络谱中均应具备幅值优势。但是,在转速较低的区域,其二倍频有可能在幅值上超过瞬时故障特征(如图1(a)所示)。这将无法确保利用传统的峰值搜索算法[10]能够在每一时刻均获取IFCF。为此,本节提出基于幅值重调的峰值搜索算法如下:
1)调整所有的瞬时包络谱的幅值:以第i时刻对应的瞬时包络谱eXi为例,将其中每一根谱线的幅值调整为其本身与二倍频和三倍频的幅值和:
eXi(j)*=eXi(j)+eXi(2*j)+eXi(3*j)
(8)
式中eXi(j)*为第i时刻对应的瞬时包络谱第j根谱线经过调整后的幅值;j为包络谱中的谱值序号,若3*j超出瞬时包络时频谱的长度则保持原幅值。
通过上述调整,瞬时包络谱中瞬时故障特征频率的幅值变为其本身与二倍和三倍频幅值之和。其二倍频的幅值则变为二倍,四倍与六倍频幅值的和。这样,瞬时故障特征频率处的新幅值就将大于二倍频对应的新幅值。因为类似四倍和六倍这样的高阶分量的幅值将远小于二倍和三倍这样的低阶倍频分量。
2)利用下式在幅值重调后的包络时频谱中对IFCF趋势线进行提取
(9)

图1(a)为低转速区下轻微故障轴承瞬时包络谱:其瞬时故障特征频率的幅值略小于其二阶倍频。图1(b)则为幅值重调的瞬时包络谱结果。其中以FCF指向的一阶瞬时故障特征频率将重新具备幅值优势,从而保证IFCF趋势线的提取。

图1 基于幅值重调的峰值搜索算法效果
第3步 以IFCF趋势线为基础,应用传统算法对原信号进行重采样。
本文将以IFCF趋势线为基础的重采样过程称为故障相角域(Fault Phase Angle, FPA)重采样,其基本算法流程如下:
(1)利用三次多项式对IFCF趋势线进行拟合,得到其相对时间变化规律为f(t);
(2)利用下式确定原始采样点在故障相角域中的坐标值

(10)
式中φ表示在时间t内转过的故障相角值。
(3)以最低瞬时故障特征频率为基准,在高于该基准的数据段插入多于原始数据点的数值来实现故障相角域的重采样。相应的采样频率fFPA为
(11)
第4步 利用被监测轴承的故障特征因子构造故障特征阶比模板实现滚动轴承的故障诊断。
本文将故障相角域重采样结果的包络谱称为故障特征阶比(Fault Characteristic Order,FCO)谱。它实际上是传统角域阶比谱的等比例压缩版本,相应的压缩比例为故障特征因子(FCC)。其中,故障特征频率峰值所对应的横坐标被统一地压缩到单位“1”处。如果被监测轴承存在故障,FCO谱中代表故障特征频率及其倍频的峰值将会出现在单位阶比(“1”)及其倍频(“2,3,…”)处。该特点为提出统一的模板直接对滚动轴承的运行状态和故障位置进行判断提供可能性。
但是,在FCO谱的整数阶比处存在峰值只能用于判断被监测滚动轴承存在故障。而要想确定故障类型则必须确定表征轴承转频的故障阶比值。与被压缩到单位“1”处的故障特征频率类似的是,表征转频的阶比值将被压缩到单位“1”以下,其横坐标值则为对应故障特征频率因子的倒数(1/FCC)。其倍频峰值对应的横坐标值为2/FCC,3/FCC,…。与故障特征频率不同的是,轴承转频以及倍频峰值往往不突出。这一特性也将为确定表征轴承转频的故障阶比峰值增加了难度。针对这一问题,本文将利用一个普遍存在却常常被忽视的现象帮助确定表征滚动轴承转频的故障特征阶比值。
如前文所述,由故障引起的高频共振将会调制故障特征频率。同理,故障特征频率也会调制较低的轴承转频。本文将这一现象称为双调制现象,其具体表现为由故障引起的共振高频调制故障特征频率,而故障特征频率又会调制轴承转频。该现象在包络谱中的体现则是在故障特征频率峰值的两侧将出现以轴承转频大小为边带的一对峰值。该现象同样会出现在FCO谱中:在代表轴承故障特征频率的单位阶比两侧将出现与单位故障阶比峰值距离相等的边带,而这两个边带到单位阶比峰值的距离则为代表轴承转频的阶比坐标值。本文将该边带称为转频阶比边带(Rotational Order Sideband,ROS)。因此,FCO谱应具备以下特点:
(1)表征故障特征频率及其倍频的故障特征阶比峰值将出现在1阶,2阶及更高的整数阶比处;
(2)代表轴承转频及其倍频的阶比值则会出现在1/FCC及其倍频处(FCC可由式(4)~(6)确定);
(3)在代表故障特征频率的整数阶比两侧将出现距离为1/FCC的左右边带。
利用以上3个特点,本文构造的故障特征阶比模板如图2所示。

图2 故障特征阶比模板Fig.2 Fault characteristic order template
在图2所示的模板中,fr,2fr和3fr分别表示代表轴承转频的阶比值及其倍频;FCO,2×FCO与3×FCO代表故障特征频率及其倍频;ROS和2ROS分别表示转频阶比边带及其2倍频。其中,以虚线红色箭头标识的2fr和3fr与2ROS在实际的FCO谱中可能因幅值过小并不明显。必须说明的是,图2仅为故障特征阶比模板的代表,实际fr与ROS对应的坐标值必须由被监测滚动轴承的几何参数计算得出。在实际应用中,只需将FCO谱与故障特征阶比模板相比较即可确定被监测轴承的运行状态和故障位置。
上述4个步骤构成了基于IFCF趋势线和故障特征阶比模板的变转速滚动轴承的故障诊断算法。图3为对应的算法流程图。

图3 算法流程图Fig.3 Flowchart of algorithm
2 仿真分析
为验证本文所提出的算法,本节以文献[15]中建立的故障轴承模型为基础,考虑变转速影响与双调制现象构造仿真信号如下
x(t)=[1+cos(2π×fr(t)×t)]*
(12)
式中 乘号“*”之前的部分模拟的是双调制现象;之后的部分则为变转速故障轴承的仿真信号;σ(t)代表噪声部分。fr(t)表示轴承转频随时间的变化规律;N为由故障引起的冲击总数;Am为第m个冲击的幅值(本节将降速模式下轴承故障引起的冲击幅值与时间的关系简化为线性关系:λ*tm,λ则为对应的比例系数);u(t)为单位阶跃函数;β为结构衰减系数;ωr为由轴承故障激起的共振频率;tm为第m个冲击出现的时间,可由式(13)的递推公式确定
(13)
式中μ为由滚动体滑移带来的误差系数,其取值范围通常为0.01~0.02。其转速由25 Hz下降为15 Hz,对应的变化规律为f(t)=-2.5t+25。仿真信号的其他参数如表2所示。图4为根据预设的故障特征因子(3.7)构造故障特征阶比模板。其中,表征故障特征频率阶比值为1,2和3(由1×FCO,2×FCO和3×FCO表示);表征轴承转频的阶比值则为0.270 3=1/3.7(由fr表示);代表转频阶比边带的峰值则为0.729 7(左边带)和1.270 3(右边带)(由ROS表示)。

表1 滚动轴承仿真信号相关参数
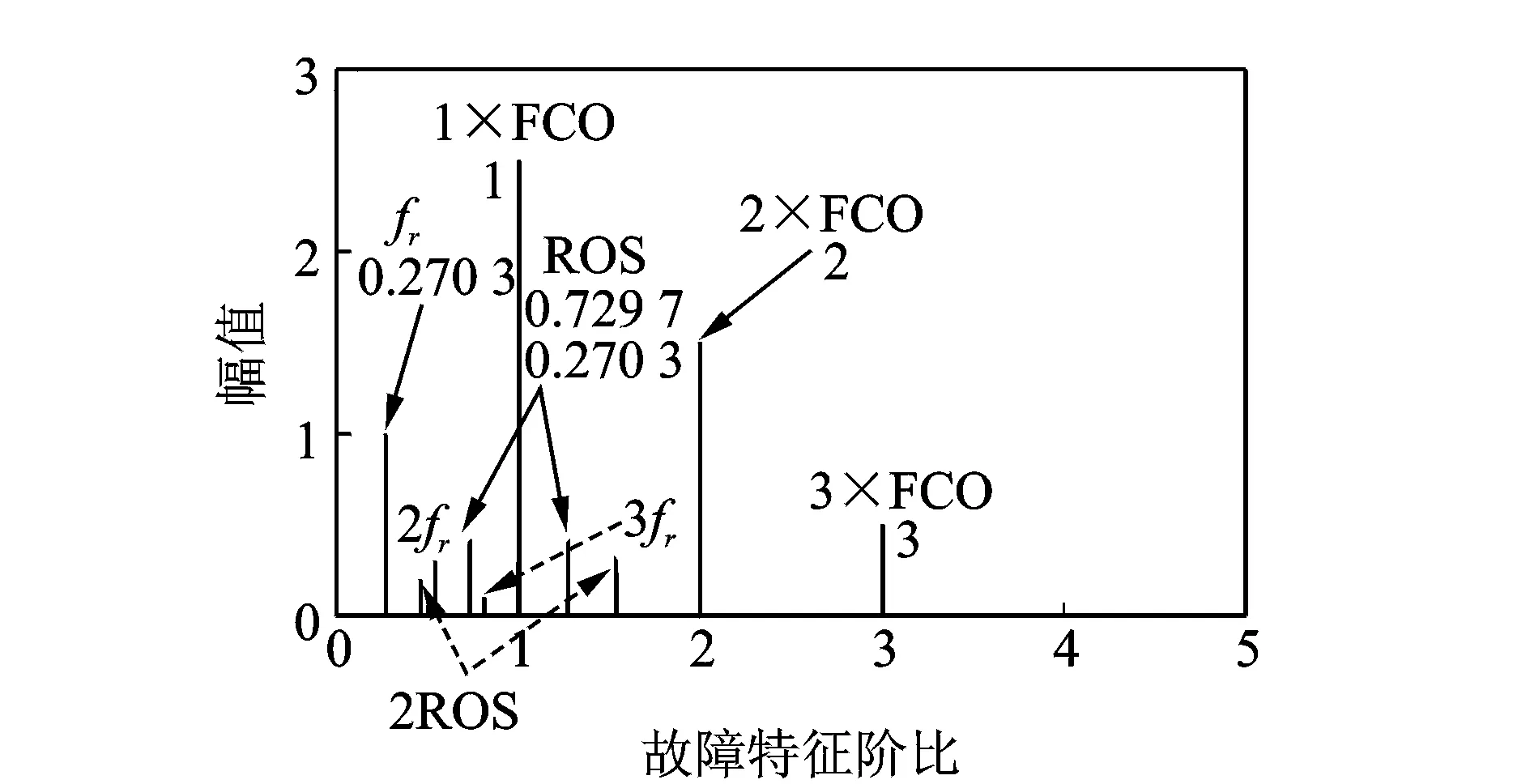
图4 仿真信号故障特征阶比模板 Fig.4 Fault characteristic order template of simulated signal

图5 仿真信号波形Fig.5 Waveform of simulated signal

图6 仿真信号的Kurtogram图Fig.6 Kurtogram of the simulated signal

图7 滤波后的包络时频谱Fig.7 Filtered envelope TFR
图5为仿真信号波形,其预设转速在图8中以下方的直线表示。图6为原始信号的Kurtogram。其中谱峭度最大值出现在中心频率为4 166 Hz,带宽为1 666 Hz,尺度为2.5的位置,与预设的4 000 Hz的共振频率基本重合。
图7则为在谱峭度滤波结果基础上得到的包络时频谱。从中可以找出明显的随时间下降的IFCF趋势线,且利用上文提出的基于幅值重调的峰值搜索算法可以对其进行提取。图8将IFCF趋势线与预设的转频趋势线进行比较:二者随时间的变化趋势相同,相互间的比例也不随时间变化。利用IFCF趋势线对原始信号进行故障相角域重采样,并利用傅里叶变换得到最终用于轴承故障诊断的FCO谱(如图9所示)。

图8 IFCF趋势线vs预设的转频趋势线Fig.8 IFCF trend vs preset IRF trend

图9 仿真信号的FCO谱Fig.9 The FCO spectrum of the simulated signal
将图9所示的FCO谱与图4所示的故障特征阶比模板做比较可以看出:在FCO谱的1,2,3阶比处(实际为1.002,2.006,3.01)存在明显的代表故障特征频率及其倍频的峰值;在0.270 3阶比处(实际为0.271 3)存在明显的代表轴承转频的峰值;在1阶故障特征阶比两侧的0.729 7和1.270 3阶比处(实际为0.730 6,1.273)存在明显的代表转频阶比边带的左右两个峰值。可以看出,FCO谱与故障特征阶比模板几乎一致,据此完成对滚动轴承的故障诊断。
3 实测故障轴承信号分析

图10 试验台结构Fig.10 Experimental set-up of the test rig
本节利用图10所示的实验台测取两组外圈故障滚动轴承的振动信号(中度故障和轻度故障)验证本文提出算法的。被测轴承的几何参数与故障特征因子如表2所示;构造外圈和内圈故障特征阶比模板如图11所示。在外圈故障特征阶比模板中,表征转频的阶比峰值横坐标为0.39,表征转频阶比边带的峰值分别为0.61和1.29;而在内圈故障特征阶比模板中,表征fr的坐标值为0.224,而表征ROS左右边带的峰值则分别为0.776和1.224。

表2 滚动轴承及实验相关参数
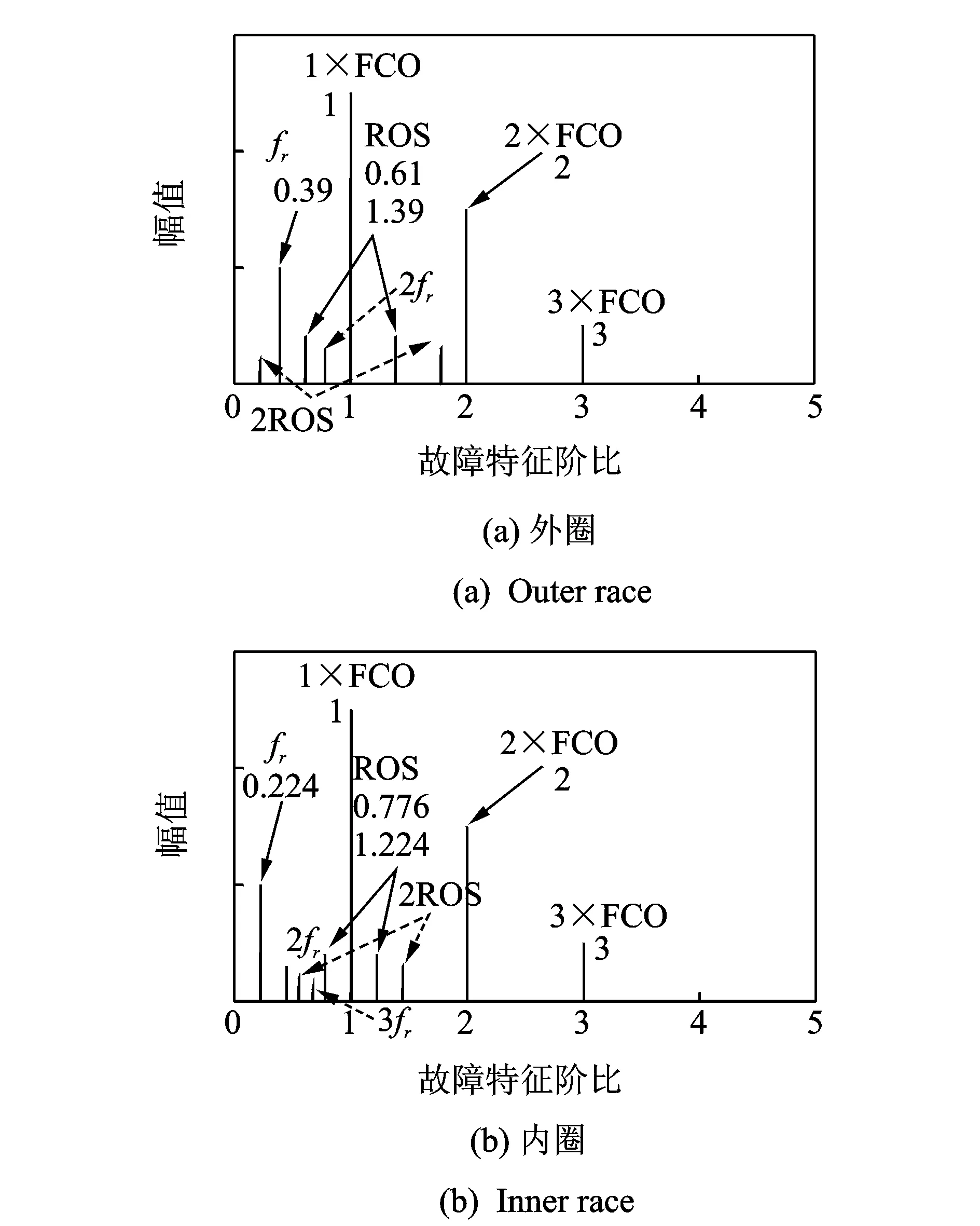
图11 故障特征阶比模板Fig.11 Fault characteristic order template
图12为中度外圈故障滚动轴承升速振动信号。由图13所示的Kurtogram可以看出,在中心频率为7 500 Hz,带宽为3 000 Hz,尺度为2处获得最大的谱峭度值(2.3)。利用上述滤波参数对原信号进行带通滤波,滤波结果的包络时频谱如图14所示。

图12 实际信号波形Fig.12 Waveform of the real vibration signal

图13 实际信号的Kurtogram图Fig.13 The Kurtogram of the real vibration signal

图14 滤波后的包络时频谱Fig.14 Filtered envelope TFR

图15 IFCF趋势线vs测取的转频趋势线Fig.15 IFCF trend vs Measured IRF trend
利用基于幅值重调的峰值提取算法可提取IFCF趋势线。图15将IFCF趋势线和利用转速计测取的轴承瞬时转频趋势进行对比。可以看出,这2个趋势线将随时间同步变化,且二者间的比例系数不随时间变化。利用IFCF趋势线对原始信号进行故障相角域重采样,能够得到最终用于故障诊断的FCO谱(如图16所示)。

图16 实际信号的FCO谱Fig.16 FCO spectrum of the real signal
在图16中,能够在单位故障特征阶比及其倍频上找到坐标值为0.999 1,1.992和2.985的峰值;在坐标值为0.39处能够找到表征轴承转频的峰值;在单位故障特征阶比两侧找到坐标值为0.611和1.389的左右转频阶比边带峰值。通过与图11中的故障特征模板项对比可以看出,图16所示的FCO谱与图11(a)所示的外圈故障特征阶比模板几乎相同。因此,可以判断出被监测轴承的外圈存在故障。
图17为外圈存在相对微弱故障的滚动轴承振动信号波形,其转速变化范围为44.5~76.9 Hz。由图18所示的Kurtogram可以看出,在中心频率为9 500 Hz,带宽为1 000 Hz,尺度为3.5处获得最大的谱峭度值(1.34)。其值低于由图13获得的最大谱峭度值(2.3)的原因则为相对微弱的故障程度。由图19所示的包络时频谱中能够找到清晰的随时间上升的趋势(IFCF趋势线)。图20将提取到的IFCF趋势线与利用转速计测取的瞬时转频趋势线进行对比。可以看出,两趋势随时间的变化趋势基本相同。

图17 实际信号波形Fig.17 Waveform of the real vibration signal
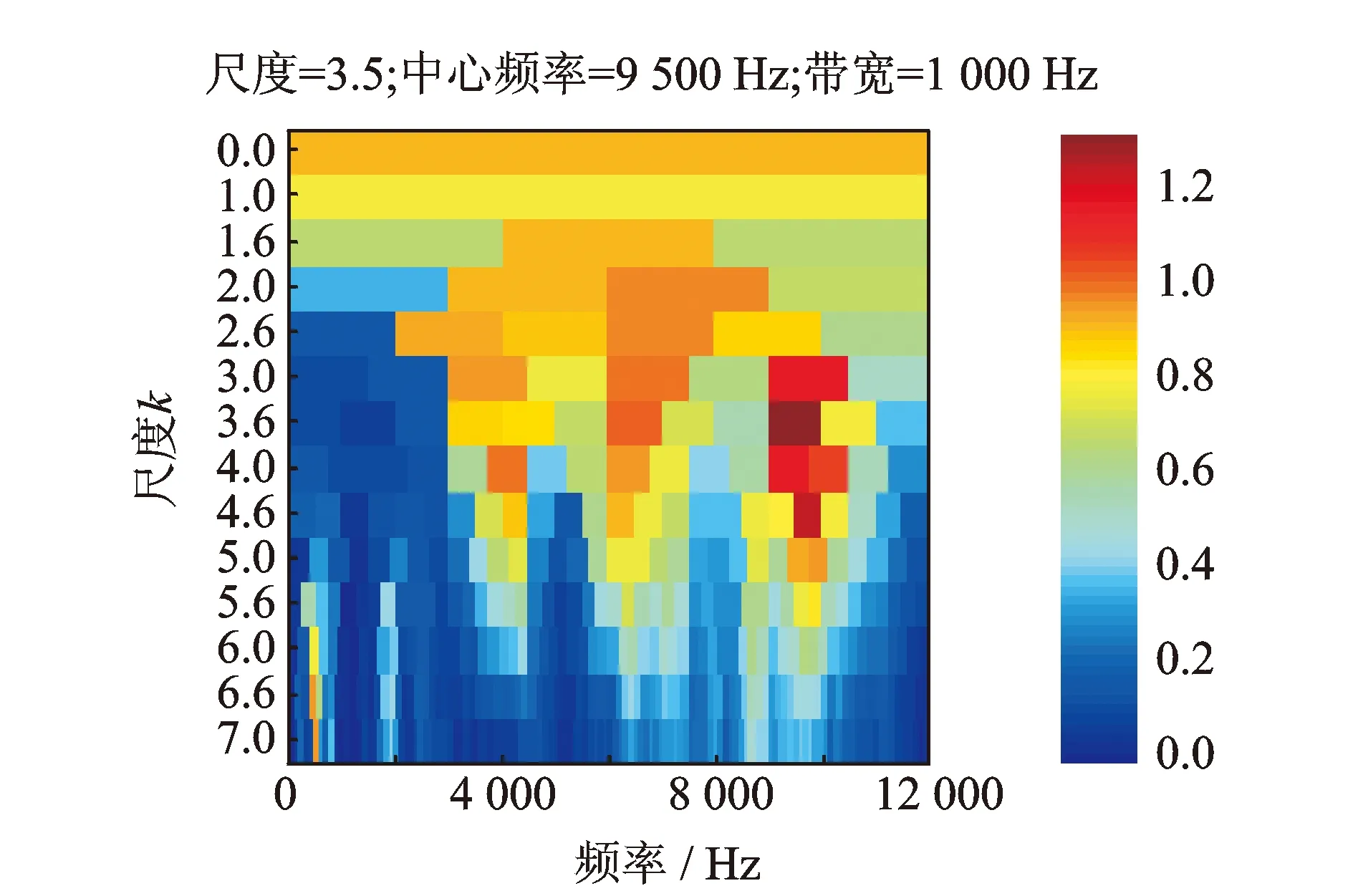
图18 实际信号的Kurtogram图Fig.18 The Kurtogram of the real vibration signal

图19 滤波后的包络时频谱Fig.19 Filtered envelope TFR

图20 IFCF趋势线vs测取的转频趋势线Fig.20 IFCF trend vs Measured IRF trend

图21 实际信号的FCO谱Fig.21 FCO spectrum of the real signal
图21为最终的FCO谱。其中,表征故障特征频率及其倍频的峰值1×FCO,2×FCO和3×FCO的横坐标值分别为1.002,2.011和2.996;表征转频阶比边带的峰值坐标则为0.611 7和1.389;表征转频的峰值坐标0.39也非常突出。将该FCO谱与预设的故障特征阶比模板进行对比仍然能够判断轴承的外圈存在故障。
4 结 论
本文提出基于故障特征阶比模板的算法以实现不利用辅助设备的变转速滚动轴承故障诊断。主要工作包括:利用故障特征因子构造故障特征阶比模板,确定滤波参数,获取包含明显趋势包络时频谱,提取IFCF趋势线,故障相角域重采样,求取FCO谱,通过对比确定滚动轴承的运行状态及故障位置:
(1)变转速运行模式下,滚动轴承的IFCF趋势线可以作为转频趋势的等效参量以代替难以获取的转频实现重采样;
(2)基于谱峭度滤波与基于幅值重调的峰值搜索算法能够从原信号的包络时频谱中对IFCF趋势线进行提取;
(3)基于IFCF趋势线的FCO谱中,表征故障特征频率及其倍频的阶比峰值将出现在单位阶比及其倍频处,表征转频的特征阶比将出现在1/FCC处,表征转频阶比边带的峰值与单位阶比的距离也为1/FCC。
(4)通过将FCO谱与故障特征阶比模板做比较,能够实现不依靠转速设备的变转速滚动轴承的故障诊断。
需要说明的是,本文提出的算法并不适合转速变化速度过快或突变的工况。
[1] Mcfadden P D, Smith J D. Vibration monitoring of rolling element bearings by the high-frequency resonance technique——a review[J]. Tribology International,1984, 17(1): 3—10.
[2] 彭富强,于德介,罗洁思,等. 基于多尺度线调频基稀疏信号分解的轴承故障诊断[J]. 机械工程学报. 2010, 46(7): 88—95.
PENG Fuqiang ,YU Dejie, LUO Jiesi,et al. Sparse signal decomposition method based on multi-scale chirplet and its application to bearing fault diagnosis [J]. Journal of Mechanical Engineering, 2010,46(7): 88—95.
[3] Urbanek J, Barszcz T, Antoni J. A two-step procedure for estimation of instantaneous rotational speed with large fluctuations[J]. Mechanical Systems and Signal Processing,2013, 38(1): 96—102.
[4] Li C, Liang M. Time-frequency signal analysis for gearbox fault diagnosis using a generalized synchrosqueezing transform[J]. Mechanical Systems and Signal Processing,2012, 26(0): 205—217.
[5] Combet F, Zimroz R. A new method for the estimation of the instantaneous speed relative fluctuation in a vibration signal based on the short time scale transform[J]. Mechanical Systems and Signal Processing, 2009, 23(4): 1 382—1 397.
[6] Fyfe K R, Munck E D S. Analysis of computed order tracking[J]. Mechanical Systems and Signal Processing, 1997, 11(2): 187—205.
[7] Borghesani P, Ricci R, Chatterton S, et al. A new procedure for using envelope analysis for rolling element bearing diagnostics in variable operating conditions[J]. Mechanical Systems and Signal Processing, 2013, 38(1): 23—35.
[8] Renaudin L, Bonnardot F, Musy O, et al. Natural roller bearing fault detection by angular measurement of true instantaneous angular speed[J]. Mechanical systems and Signal Processing, 2010, 24(7): 1 998—2 011.
[9] Cheng W, Gao R X, Wang J, et al. Envelope deformation in computed order tracking and error in order analysis[J]. Mechanical Systems and Signal Processing, 2014, 48(1-2): 92—102.
[10]郭瑜,秦树人,汤宝平,等. 基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报. 2003, 39(3): 32—36.
GUO Yu, QIN Shuren, TANG Baoping, et al. Order tracking of rotating machinery based on instantaneous frequency estimation[J]. Journal of Mechanical Engineering,2003, 39(3): 32—36.
[11]Bonnardot F, El Badaoui M, Randall R B, et al. Use of the acceleration signal of a gearbox in order to perform angular resampling (with limited speed fluctuation)[J]. Mechanical Systems and Signal Processing. 2005, 19(4): 766—785.
[12]Urbanek J, Barszcz T, Sawalhi N, et al. Comparison of amplitude-based and phase-based methods for speed tracking in application to wind turbines[J]. Metrology and Measurement Systems, 2011, XVIII: 295—304.
[13]赵晓平,赵秀莉,侯荣涛,等. 一种新的旋转机械升降速阶段振动信号的瞬时频率估计算法[J]. 机械工程学报,2011, 47(7): 103—108.
ZHAO Xiaoping, ZHAO Xiuli, HOU Rongtao, et al. A new method for instantaneous frequency estimation of Run-up or Run-down vibration signal for rotating machinery[J]. Journal of Mechanical Engineering,2011, 47(7): 103—108.
[14]Antoni J. The spectral Kurtosis: a useful tool for characterising non-stationary signals[J]. Mechanical Systems and Signal Processing, 2006, 20(2): 282—307.
[15]Liang M, Soltani Bozchalooi I. An energy operator approach to joint application of amplitude and frequency-demodulations for bearing fault detection[J]. Mechanical Systems and Signal Processing, 2010, 24(5): 1 473—1 494.
The instantaneous fault characteristic frequency and fault characteristic order template based fault diagnosis algorithm for rolling bearing under time-varying rotational speed
WANGTian-yang1,LIJian-yong2,CHENGWei-dong2
(1.Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China; 2.School of Mechanical Electronic and Control Engineering, Beijng Jiaotong University, Beijing 100044, China)
To solve the problem that there exist no clear and prominent components related to rolling bearing rotational frequency in the time-frequency representation, the instantaneous fault characteristic frequency from the envelope TFR is used as the substitute of the traditional rotational frequency to fulfill the resampling process and then a fault diagnosis algorithm for the rolling bearing based on the fault characteristic order template is proposed to accomplish the final bearing diagnosis. In specific, the proposed algorithm can be summarized as four parts: (1) The spectral kurtosis based filtering, together with the short time Fourier transform (STFT) can lead to the envelope TFR, (2) A revised peak searching algorithm is then used to extract the IFCF trend from the envelope TFR, (3) The resampling step is then carried on using the IFCF trend and the fault characteristic order (FCO) spectrum in the fault phase angle domain is obtained, (4) The fault characteristic order template based on the fault characteristic coefficient (FCC) is finally constructed to recognize the operating state of the rolling bearing under time-varying rotational speed and identifying its corresponding fault type. The effectiveness of the proposed method has been validated by both simulated and experimental bearing vibration signals.
fault diagnosis; rolling bearing; fault phase angle domain; fault characteristic order spectrum; rotational order sideband
2014-04-28;
2014-08-25
国家自然科学基金资助项目(面上项目,重点项目,重大项目)(51275030)
TH165+.3;TH133.33
A
1004-4523(2015)06-1006-09
10.16385/j.cnki.issn.1004-4523.2015.06.020
王天杨(1985—),男,博士研究生。电话: 13581583746; E-mail: wty19850925@126.com

