现代排序论应用*
唐国春,井彩霞
①上海第二工业大学经济管理学院,上海 201209;②天津工业大学管理学院,天津 300387
现代排序论应用*
唐国春①†,井彩霞②
①上海第二工业大学经济管理学院,上海 201209;②天津工业大学管理学院,天津 300387
排序是为加工若干个工件而对工件及其所需要的机器按时间进行分配和安排,在完成所有工件加工时使得某个(些)目标为最优。在过去几十年里,排序论的研究进展迅速。简述排序论在中国的发展历程,介绍现代排序论在三个代表性领域的应用:供应链排序、半导体生产中的排序和手术排程,并展望未来的发展。
排序;供应链;半导体/晶圆;手术
第二次世界大战期间运筹学兴起,首次把运作(operation)作为研究对象。其间,研究运作的时间安排促成了排序(scheduling)概念的建立和研究的开展。在20世纪中叶运筹学奠基时期,排序论的先驱工作已经在离散优化领域占有重要地位。此后,排序论始终保持蓬勃发展的势态。
20世纪60年代越民义就注意到排序问题的重要性和在理论上的难度。1963年他编写了国内第一本排序论讲义。70年代初他和韩继业研究同顺序流水作业排序问题[1],开创了中国研究排序论的先河。在他们两位的倡导和带动下国内排序论的理论研究和应用研究有了较大的发展。国内自动化学科把“scheduling”译为“调度”始于1983年[2]。调度有太宽泛的涵义,1978年《现代汉语词典》对于“调度”的解释是“管理并安排(工作、人力、车辆等)”[3],是指对实际过程的具体操作。考虑到在数学和运筹学中50年来使用的习惯,我们赞同把“scheduling”译成“排序”。虽然“调度”不是数学上的术语[4],我们也尊重自动化学科使用“调度”的译法。所以,我们提倡用“排序”和“调度”作为“scheduling”的中文译名。苏步青院士曾为排序专业委员会(排序分会)题签《排序通讯》和《排序论学报》,激励大家学习和研究排序论[5]。国家自然科学基金委员会学科代码G010302是排序、排队论和存储论[6]。
排序论开创者之一Baker指出:“排序领域内许多早期的工作是在制造业推动下发展起来的,所以在描述排序问题时会很自然地使用制造业的术语。虽然排序问题在许多非制造业的领域内取得相当有意义的成果,但是制造业的术语仍然经常在使用。因而,往往把资源(resource)称为机器(machine),把任务(task)称为工件(job)。有时工件由几个受先后次序约束的基本任务所组成,这种基本任务称为工序(operations)。例如,把门诊病人到医疗诊所看病的排序问题也描述成为‘工件’在‘机器’上‘加工’的过程”[7]。排序论中的“机器”和“工件”已经不是机器制造业中的“车床”和“车床加工的螺丝”,已经从“车床”和“螺丝”等具体事物中抽象出来,是抽象的代表性概念。排序论中的“工件”可以是任务、非圆齿轮、计算机终端、患者、降落的飞机等,“机器”可以是完成任务所需要的人财物资源、数控机床、计算机中央处理器(CPU)、医生、机场跑道等。例如:计算机科学中并行计算机的出现,促进排序论中对平行机(parallel machine)排序的深入研究;反过来,排序论中的平行机可以应用到计算机科学的并行计算中去,平行机排序的成果在一定程度上推动并行计算和并行计算机的发展[8]。Baker指出:“排序是为完成一些任务而对所需资源按时间进行分配。”“排序要做出决策,要回答两个问题:①哪些资源要分配以完成每项任务;②何时完成每项任务。”[7]Pinedo在著名的《Scheduling: Theory,Algorithms,and Systems》一书中提出几乎相同的看法,“排序是按时间把稀缺资源分配给要完成的任务[9]。因而,按时间分配工件(任务)和机器(资源)是排序很本质的特征。
工件何时就绪,何时开始加工,何时中断加工(preempt),何时更换工件,何时再继续加工原工件;机器何时就绪,何时进行加工,何时空闲(idle),何时更换机器等等,这些都是按时间进行分配和安排。单纯的分配问题,是单纯地把工件分配给机器以便进行加工,是一个数学规划问题。单纯的次序安排问题是sequencing问题。从最优化的角度我们给排序如下的定义:排序是为加工若干个工件,而对工件及其所需要的机器按时间进行分配和安排,在完成所有工件加工时使得某个(些)目标为最优。
因此,在数学、运筹与管理、自动化、工业工程的范畴里,“排序”默认的涵义是“scheduling”,而且是指“机器排序(machine scheduling)”。“Sequencing”译成“安排次序”,是一种特殊的“scheduling”,是只要确定工件的次序就完全确定加工的时间表(schedule)问题,因此,排序论学科的定位是机器排序的理论和应用。除了机器排序之外,还有项目排序(project scheduling)和数据排序(sorting)。项目排序包括CPM(关键路线法)和PERT(计划评审技术)。数据排序又称为整序,是更为特殊的一类sequencing问题,仅仅是一些“元素”(即“工件”)按照某种要求重新安排次序的问题,并不涉及到“机器”的因素,例如冒泡排序和快速排序等。此外,“timetabling”也是“安排时间表”,是指安排课程表,安排(火车或飞机)时刻表等。与作为最优化问题的scheduling不同,timetabling主要解决的是“存在性”问题,是判别和设计是否存在符合某些要求的时间表[8]。
如果按数学分为理论数学和应用数学,那么排序论可以分为排序的理论部分和排序的应用部分。排序的理论部分又可分为经典排序(classical scheduling)和现代排序(modern scheduling)。Brucker和Knust在《Complexity Results of Scheduling Problems》[10]中使用classical和extended两个词来区别经典的和非经典的两类排序问题。他们也用新型排序来表示非经典的排序问题,这也就是Potts等称为Enhanced(扩展的)排序问题[11]。因此,现代排序就是非经典的、推广的、扩展的,也就是新型的排序[8],是排序论学科发展史上第五个十年的研究主题[11]。
现代排序是相对经典排序而言,其特征是突破经典排序的基本假设。根据1993年Lawler等的观点,经典排序有4个基本假设[12]:①单资源。机器是加工工件所需要的一种资源。一台机器在任何时刻最多只能加工一个工件;一个工件在任何时刻至多在一台机器上加工。作为这个基本假设的突破,有成组批量排序、同时加工排序(又称为分批排序)、不同时开工排序和资源受限排序等。②确定性。决定排序问题的一个实例的所有(输入)参数都是事先知道的和完全确定的。作为这个基本假设的突破,有可控排序、随机排序、模糊排序和在线排序等。③可运算性。我们是在可以运算和计算的程度上研究排序问题,而不去顾及诸如如何确定工件的交货期,如何购置机器和配备设备等技术上可能发生的问题。如果考虑实际应用中有关的情况和因素,就是应用排序问题。④单目标和正则性。排序的目的是使衡量排法好坏的一个一维目标函数的函数值为最小,而且这个目标函数是工件完工时间的非降函数。这就是所谓正则目标。多目标排序、准时排序和窗时排序等是这个假设的突破。
因此,上述10种经过推广的排序(可控排序、成组批量排序、在线排序、同时加工排序、准时排序和窗时排序、不同时开工排序、资源受限排序、随机排序、模糊排序、多目标排序等)就构成现代排序的主要内容[8]。当然,这10种排序不可能包括层出不穷、不断涌现的新型排序,没有涉及到的新型排序有工件加工时间随加工次序变动的排序和多台机器同时加工工件的排序等。
1 供应链排序
供应链是围绕核心企业,通过对信息流、物流、资金流等的控制,从采购原材料,到中间产品(或者中间服务)、最终产品(或者最终服务),最后由销售网络把产品(或者服务)送到客户,是供应商、制造商、分销商、零售商,直到客户形成的网链结构。这类网链结构的设计、协调、优化是供应链管理的主要任务。供应链排序是集成研究供应链管理中生产(或者服务)的排序、分批和发送,是排序论在供应链管理中的应用[13]。
供应链排序前端的供应商问题是研究供应商如何安排生产和如何把工件分批并发送给制造商,使生产排序费用和发送费用的总费用为最小。供应链排序后端的制造商问题是研究制造商如何安排生产和如何把工件分批并发送给客户,使生产排序费用和发送费用的总费用为最小。把供应链排序前端和后端一起研究的问题称为联合问题[13]。
树形供应链是指在供应链中只有一个供应商,这个供应商要为多个制造商加工和发送工件(货物)。供应商对工件进行加工时,需要一定的生产排序费用;在安排发送货物时,又需要一定的发送费用。我们的目标是使排序费用和发送费用的总和(简称为总费用)为最小。我们假定每发送一批货物的费用只与发送给哪个制造商有关,而与发送了多少货物无关,也就是说,对于同一个制造商来说,供应商每次发送的费用是一个常数。但是,每次最多能够发送的货物数量有一个上限,我们称之为发送能力。因此,为减少发送费用,需要把发送给同一个制造商的货物分成若干批,然后按批进行发送。由于是成批发送,所以这批中每个工件的完工时间应该是它所在的批中所有工件都加工完成的时刻,也就是等于这批中最后一个工件的完工时间。这个完工时间称为是这个批的完工时间。一般来讲,存在具有以下性质的最优排序:
(1) 供应商加工任何两个工件之间没有空闲;
(2) 每一批的发送都发生在这批工件中的某一个工件的完工时间;
(3) 从供应商发送一批工件给制造商时,这批工件在供应商处是接连加工的。
这就可以缩小搜索的范围。
其他还有多供应商供应链排序、多运输方式供应链排序等等,可以参考专门的论文。例如,在供应链排序中,工件加工后分批发送给下游客户的运输方式有多种,供应商不仅需要确定工件加工顺序和分批方式,还要确定运输方式,使加工和运输总费用最少。这就是多运输方式供应链排序[13]。
2 半导体生产中的排序问题
晶圆是硅半导体集成电路制作所用的硅晶片。晶圆的生产中有三类特殊的排序问题:工件可重入排序、多功能机排序和同时加工排序。
(1) 可重入排序
可重入(Re-entrance)是晶圆生产最典型的特点(图1)。每个晶圆都由具有相似工艺的不同层组成,因此,晶圆会多次重复访问相同的机器以完成不同层的加工。正是由于这种重入的特性,半导体生产系统被称为是不同于传统的流水作业(flow shop)和异序作业(job shop)的“第三类生产方式”[14]。
对于多重入的单台机器排序问题,可以利用工件的重入特性和具有平行链约束之间的关系,分别给出在总带权完工时间和最大费用函数两个目标函数下的多项式时间最优算法[15]。其他流水作业[16]、异序作业[17]等更为复杂机器的多重入可以参考有关的论文。
除了半导体生产外,在信号处理、印刷电路板[18]以及桥梁建造[19]等等许多领域也会发生加工“可重入”情况。
(2) 多功能机排序问题
半导体晶圆种类繁多,工序复杂。有些工序要求在指定的机台上加工,而不是所有机台都能加工。另一方面,同一台机器上加工不同种类的晶圆,需要一个安装时间。这个安装时间是更换模具(光罩)的时间,也可能是调整加工条件(如温度、气体密度等)所需的时间。这就是需要安装时间的多功能机(multi-purpose machine)排序[20]。
多功能机排序问题中工件组与机器之间的对应关系见图2,其中左边表示有7个工件组,右边表示有5台平行机器。如果工件组和机器之间有向量连接,则表示该工件组中的工件可以在相应的机器上加工,否则这台机器不能加工该组工件。同组的工件在机器上接连加工时不需要安装时间;不同组的工件接连加工时需要一个安装时间。同组中的工件不一定要接连加工,并且每台机器在加工第一个工件前,也需要安装时间。我们要寻找加工方案,使最后完工的工件尽可能提前。
多功能机排序在实际应用中还要考虑机器安装的次数。在半导体晶圆生产车间中更换光罩或调整加工条件都需要人为地去操作,而且安装上新的光罩以后还需要有一个适应的过程,也就是说新光罩下最初的几批晶圆有可能是不达标的,所以有时宁可牺牲完工时间,也不愿意频繁地调整机器。这就是两个目标的多功能机排序问题,其中一个目标是使最后完工的工件尽可能提前,另一个目标是使安装次数为最少[21]。
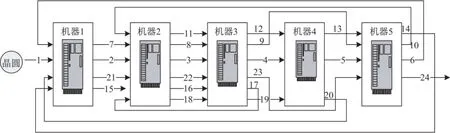
图1 可重入加工示意图
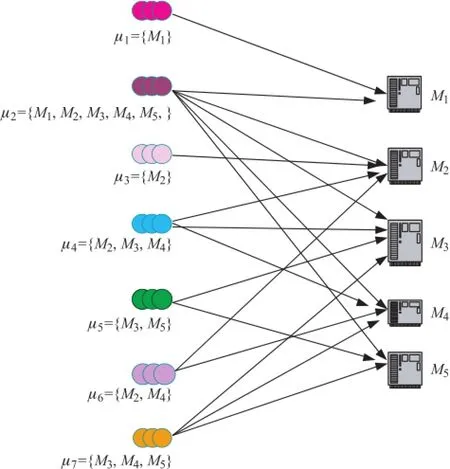
图2 多功能机排序中工件与机器的对应关系
(3) 同时加工排序
同时加工排序又称为分批排序,产生于20世纪90年代大规模的现代化生产流水作业线,并很快被应用到航空工业、钢铁铸造、冶金、电镀甚至制鞋业等许多领域。半导体晶圆生产是分批排序应用最广泛的领域。分批排序主要有三种模型:批加工时间为该批中最大工件加工时间的并行批(parallel batch),批加工时间为该批中工件加工时间之和的串行批(serial batch)及批加工时间为常数的模型。常见的也是默认的分批模型是并行批排序模型。并行批排序模型源于晶圆测试,是把晶圆放入烤箱烘烤(图3,不同的形状代表不同种类的晶圆),每个晶圆都有一个最短的烘烤时间,经受住最短烘烤时间烘烤的晶圆才是合格产品。这里最短烘烤时间是指相应的晶圆多烘烤一些时间是允许的。烤箱有一个固定的容量B,并假设每种晶圆的体积为1,至多有B个晶圆可以作为一批放在烤箱内同时烘烤,烘烤过程不允许中断。每种晶圆的最短烘烤时间可能不同,为了保证质量,同一烤箱内晶圆的实际烘烤时间是所有最短烘烤时间中最长的。相对其他测试过程,烘烤的用时很长(大约是120 min,其他过程大约5 min),从而成为晶圆生产流程的瓶颈。随着半导体工业的飞速发展,竞争不断加剧,如何有效地利用组合优化工具,提出分批排序问题的好算法,以缩短产品的生产流程,提高生产效率,无疑具有重大意义。
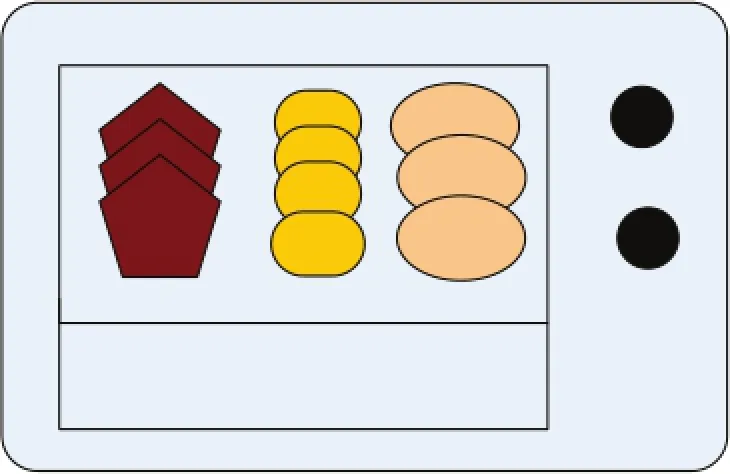
图3 烤箱示意图
3 手术排程
医院中使用设备最昂贵、动用人力资源最广泛、涉及资金最多的是手术室及其手术的管理和安排,通常称为手术排程(图4)。手术室往往是医疗总流程的瓶颈,许多患者必须等待手术完成后才能继续进行下一步的诊疗。如何高效地利用手术资源,是医院节约成本,提高工作效率,为患者提供满意服务的关键。
我们把手术患者看成是待加工的工件,把执刀医师、麻醉师、护士和手术设备等四种资源看成是实施手术同时需要的机器,那么一台手术就是需要多台机器同时进行加工的工件。如果把医院中多间手术室看成多台平行机,那么手术排程就是多台机器同时加工工件的平行机排序问题。基于理论分析,按照排序论中的算法,把执刀医师及其承担的手术分配到手术室,使得最迟结束的手术尽可能地提前,使所有的手术尽早做完,也就是使所有手术室开放的时间尽可能短。由于安排分配到手术室中手术的次序是不会改变这个手术室的开放时间的,我们还按照排序论中的算法,使得医院和患者为手术付出的总的“代价”为最小,从而提高手术相关资源的利用率。我们在排序论理论分析基础上提出算法和估计误差,用层次分析法、零和博弈和仿真技术得到反映四种资源重要性的资源权数,配合上海市第一人民医院研发计算机手术排程系统,并应用于实际,取得良好的经济和社会效益[22]。这在国内外是首创的。国际上绝大多数是建立执刀医师或(和)护士安排的数学规划(包括混合整数规划或者目标规划)的数学模型,个别有建立排序论模型,但是求解还是转化为数学规划,算法复杂,计算量大。我们这个手术排程项目获得2012年中国运筹学会第五届运筹学应用二等奖、2013年中国医院科技创新奖二等奖、2013年上海医学科技奖二等奖和2014年中华医学科技奖卫生管理奖。我们还在进一步改进手术排程的算法,在考虑到同一执刀医师的手术要接连安排,使得手术室开放的时间尽可能短和提高手术相关资源的利用率等三个目标的基础上,还要能够满足更多的要求,包括要考虑执刀医师的巡视病房和门诊的安排,要考虑手术清洁(污染)程度、麻醉方式和患者特性等等。
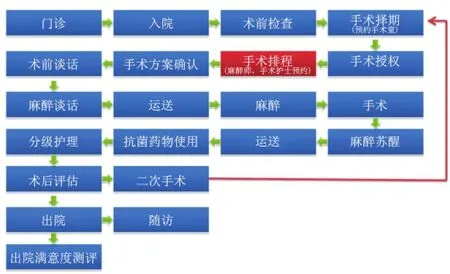
图4 医院手术流程
4 展望
排序论学科发展已经60年。经过组合分析、分支定界、计算复杂性和分类、近似算法、现代排序等五个阶段之后[11],排序论与博弈论、行为科学交叉,供应链排序、半导体生产中的排序、手术排程等许多应用研究有较大的进展。正如Potts等指出:“排序论的进展是巨大的。这些进展得益于研究人员从不同的学科(例如:数学、运筹学、管理科学、计算机科学、工程学和经济学等)所做出的贡献。排序论已经成熟,有许多理论和方法可以处理问题;排序论也是丰富的(例如,有确定性或者随机性的模型、精确的或者近似的解法、面向应用的或者基于理论的)。尽管排序论取得进展,但是在这个令人兴奋并且值得研究的领域,许多挑战仍然存在。”[11]排序论的长足发展,尤其是具有广阔应用前景的现代排序的丰硕成果,使排序论已经成为发展最迅速、研究最活跃、成果最丰硕、前景最诱人的学科领域之一。排序论作为组合优化的一个分支,将继续在运筹学的大花园里绽放出美丽的花朵。
(2013年12月18日收稿)■
[1] 越民义, 韩继业. n个零件在m台机床上的加工顺序问题(I)[J]. 中国科学, 1975, 5: 462-470.
[2] 周荣生. 汉英综合科学技术词汇[M]. 北京: 科学出版社, 1983.
[3] 中国社会科学院语言研究所词典编辑室. 现代汉语词典[M] . 上海:商务印书馆, 1978.
[4] 唐国春. 关于Scheduling中文译名的注记[J]. 系统管理学报, 2010, 19(6): 713-716.
[5] 唐国春. 一万米高空是晴天——教坛漫笔[M]. 珠海: 珠海出版社, 2011.
[6] 国家自然科学基金委员会. 国家自然科学基金申请代码[EB/OL] [2014-7-20]. http://www.nsfc.gov.cn/nsfc/cen/xmzn/2014xmzn/17.
[7] BAKER K R. Introduction to Sequencing and Scheduling [M]. New York: John Wiley & Sons, 1974.
[8] 唐国春, 张峰, 罗守成, 等. 现代排序论[M]. 上海: 上海科学普及出版社, 2003.
[9] PINEDO M L. Scheduling: theory, algorithms, and systems [M]. 3rd Edition. New York: Springer, 2008.
[10] BRUCKER P, KNUST S. Complexity results for scheduling problems[EB/OL]. (2009-6-29)[2014-7-20]. http://www.informatik. uni-osnabrueck.de/knust/class.
[11] POTTS C N, STRUSEVICH V A. Fifty years of scheduling: a survey of milestones [J]. Journal of the Operational Research Society, 2009, 60: S41-S68.
[12] LAWLER E L, LENSTRA J K, RINNOOY KAN A H G, et al. Sequencing and scheduling: Algorithms and complexity [M]//GRAVES S C, et al. Handbooks in OR & MS(Volume 4). Amsterdam: Elsevier Science Publishers B V, 1993: 445-522.
[13] 唐国春. 供应链排序的模型和方法[C]//袁亚湘, 等. 中国运筹学会第八届学术交流会论文集. 香港: Global-Link Informatics Limited, 2006: 495-502.
[14] KUMAR P R. Re-entrant lines [J]. Queuing Systems, 1993, 13: 87-110.
[15] 井彩霞, 钱省三, 唐国春. Single machine scheduling with re-entrance [J]. 运筹学学报, 2008, 12 (2): 84-87.
[16] 井彩霞, 黄婉珍, 唐国春. Minimizing total completion time for reentrant flow shop scheduling problems [J]. Theoretical Computer Science, 2011, 412(48): 6712-6719.
[17] CHEN J C, WU C C, CHEN C W, et al. Flexible job shop scheduling with parallel machines using genetic algorithm and grouping genetic algorithm [J]. Expert Systems with Applications, 2012, 39(11): 10016-10021.
[18] WANG M Y, SETHI S P, VAN DE VELDE S L. Minimizing makespan in a class of reentrant shops [J]. Oper Res, 1997, 45: 702-712.
[19] YANG D L, KUO W H, CHERN M S. Multi-family scheduling in a two-machine re-entrant flow shop with setups [J]. European J Oper Res, 2008, 187(3): 1160-1170.
[20] BRUCKER P, SCHLIE R. Job-shop scheduling with multi-purpose machine [J]. Computing, 1990, 45: 369-375.
[21] 井彩霞, 钱省三, 唐国春. 双目标函数下需要安装时间的平行多功能机排序问题[J]. 计算机集成制造系统, 2010, 16(4): 867-872.
[22] ZHONG L W, LUO S C, WU L D, et al. A two-stage approach for surgery scheduling[J]. Journal of Combinatorial Optimization, 2012, 27(3): 545-556. doi: 10.1007/s10878-012-9535-2.
Modern scheduling and its applications
TANG Guo-chun①, JING Cai-xia②
① School of Economics and Management, Shanghai Second Polytechnic University, Shanghai 201209, China; ② School of Management, Tianjin Polytechnic University, Tianjin 300387, China
Scheduling is the allocation of machines according to time in order to process the collection of jobs. It is a decision-making with the goals of optimizing one or more objectives. In the past decades, the study of scheduling has been advanced quickly. This article presentd a brief history and the recent developments of modern scheduling theory in China. Then, the applications in three focuses are prospected, namely supply chain, semiconductor manufacturing and surgical operation. A future perspective is provided at the end of the article.
scheduling, supply chain, semiconductor/wafer, surgical operation
(编辑:温文)
10.3969/j.issn.0253-9608.2015.02.006
*国家自然科学基金资助项目(71371120)和天津市高等学校人文社会科学研究项目(20132144)资助
†通信作者,E-mail:gctang@sspu.edu.cn

