地铁动荷载作用下隧道-地裂缝-地层的三维动力响应*
杨 觅,门玉明,贾朋娟
(长安大学 地质工程与测绘学院,陕西 西安 710054)
地铁动荷载作用下隧道-地裂缝-地层的三维动力响应*
杨 觅,门玉明,贾朋娟
(长安大学 地质工程与测绘学院,陕西 西安 710054)
为了探明西安地裂缝场地地铁动荷载作用下的隧道-地层动力响应特征,提出了基于ABAQUS的地铁振动响应三维模拟方法,实现了地铁多轮对荷载的移动。通过有限元计算,得到了整体式隧道的振动响应特征和振动波在地裂缝场地的传播规律,并将有无地裂缝时的振动响应进行了对比,分析了地裂缝对振动响应的影响。计算表明:单节车辆诱发振动沿纵向的影响范围不超过75 m;地铁运行诱发的振动以竖向为主,振动沿横向传播时水平振动衰减较慢;在本次模拟工况下,地裂缝的存在对地裂缝邻近约12 m范围内土体的振动影响较大,对衬砌结构的影响不显著。
地裂缝;整体式隧道;地铁荷载;动力响应;数值模拟;西安
地裂缝给西安地铁的建设带来了重大难题,许多学者对穿越地裂缝带的隧道结构措施开展了研究,取得了很多成果。目前,地铁1、2号线已于2011年和2013年相继运营。地铁的运营又带来一些新的课题,地铁振动问题以及地铁动荷载作用下隧道-地裂缝-地层的动力响应问题。
国内对地铁振动的研究,现场实测和数值模拟手段均有。对于实测,潘昌实[1]、张玉娥[2]等人对北京地铁隧道衬砌结构的振动进行了现场测试,刘卫丰[3]等人对北京地铁诱发的地面振动进行了测试,楼梦麟[4]等人对上海地铁诱发的地表振动进行了测试。从已有的文献来看,地铁振动实测集中在地铁修建较早的北京、上海、广州、南京等城市,而且振动问题已被广泛关注,因为地铁振动对沿线居民生活和古建筑的安全造成了一定的影响。在西安,钱春宇[5]等人对地铁运行引发的钟楼台基和木结构的振动进行了实测。由于西安地铁修建较晚,所以地铁振动实测偏少。在数值模拟方面,二维模拟因网格数目少,计算快捷被众多学者采用。刘建达[6]、宫全美[7]、白冰[8]、单涛涛[9]等人采用二维有限元模型分析了地铁振动问题。而Andersen[10]等人的研究表明,二维模拟只能用于地铁引起振动的定性分析。张鹤年[11]等人对地铁诱发的环境振动进行了三维有限元模拟,并与实测值进行了对比,发现二者较吻合。笔者利用ABAQUS软件分别对二维和三维的振动响应进行了模拟,发现二维模拟结果偏大,由此说明二维模拟有一定的局限性。基于此,本文在西安地裂缝的背景下,进行地铁动荷载作用下的隧道-地层三维动力响应研究。目前对西安地裂缝带地铁振动问题的研究几乎是空白,本文的研究对了解西安地铁运行诱发振动的传播特征及控制振动有一定意义。
1 模型的建立
1.1 有限元模型与材料
取隧道与地裂缝90°正交,地裂缝倾角80°,贯穿整个地层。模型上、下盘地表沿纵向长度为90 m、50 m,横向宽度为100 m,深度为50 m。二次衬砌外围宽度为9.4 m,高度为9.55 m,初衬与二衬厚度为0.3 m、0.55 m,隧道埋深15 m,有限元模型及衬砌如图1所示。衬砌与土体单元采用八节点线性六面体单元。对于单元尺寸,孟昭博[12]的研究表明,在研究黄土地区小于20 Hz的低频地铁振动时,选用1.5 m的单元长度,可以满足计算精度。为了控制计算代价,将衬砌上下部位和左右10 m范围内网格加密,最大尺寸不超过2 m,其他区域网格适当加大,横向最大尺寸为5.5 m,沿隧道纵向最大尺寸不超过2 m。

图1 有限元模型及衬砌示意图
地层静力参数采用西安地裂缝典型地段地层参数取加权平均值得到,动力参数通过西安永宁门工点的弹性波速测试结果反算获得。土层分3层,厚度分别为:10 m、20 m、20 m。各材料参数如表1所示。
地裂缝上下盘土体之间、衬砌与土之间设置接触关系。各接触面法向采用“硬”接触,即法向能传递的压力大小不受限制,切向采用库仑摩擦模型。土与土、土与衬砌之间的摩擦系数分别取0.3、0.7[13]。另外,经过软件计算可以发现,地铁动荷载不至于令土与衬砌的接触面分离,所以对各接触面进行了接触不分离的设置。在单次地铁行车荷载作用下,绝大部分土体与衬砌区域处于弹性变形状态。那么,在研究振动响应时,土和衬砌选择理想弹性本构关系。

表1 地层及衬砌物理力学参数
1.2 边界条件

1.3 模态分析
利用ABAQUS/Standard,选择Lanczos方法计算整体式隧道-地裂缝-地层模型的自振频率。其前8阶自振频率分别为:0.203 2 Hz、0.534 0 Hz、0.671 3 Hz、0.803 2 Hz、0.907 3 Hz、1.194 3 Hz、1.266 7 Hz、1.266 7 Hz。结构动力分析时材料阻尼一般选择Rayleigh阻尼。比较振型参与系数,发现y方向振型参与系数最大的最低阶振型是第2阶,x方向振型参与系数最大的最低阶振型是第1阶。本文主要研究竖向与横向的振动,因此取f1=0.203 2 Hz,f2=0.534 0 Hz来计算阻尼系数α、β。骆亚生[15]对西北地区黄土的研究表明,黄土阻尼比在0.02~0.25之间,地铁振动属于小能量振动,阻尼比相对较小,取ξ1=ξ2=0.05。得α=0.092 4 s-1、β=0.021 6 s。衬砌结构阻尼比也取0.05,则阻尼系数取值同上。模型最大固有周期为Tmax=4.9 s,一般认为增量步长不超过最大固有周期的1/100,此处取步长为0.022 5 s。
2 列车移动荷载
2.1 加载思路
三维模拟的一项关键技术就是如何实现列车荷载的移动,对于ABAQUS软件,要实现荷载移动,可以调用子程序DLOAD和UTRACLOAD,而子程序只能模拟单个均布荷载在结构面上的移动。列车轮对荷载是左右两侧成对出现的,且有多个轮对。故调用子程序的方法不适合于此。李才志等[16]提出用小块面板在结构体表面移动从而实现面荷载移动的构思,该小面板即荷载移动平台。基于这一思想,本文采用这种巧妙的方法实现了地铁多轮对荷载的移动,即“移动荷载平台”,如图2所示,此处平台是一块长薄板,列车荷载作用于薄板上,薄板的移动引起荷载也移动。单个轮对荷载可由5根轨枕共同承担[17],轮对荷载从正下方轨枕往两侧的分配比例为0.4、0.2、0.1,分布长度约2.5 m。西安地铁采用4轴的B型车,轴距2.2 m,现将列车相邻两轴的荷载合为一体,作用于长4 m,宽0.6 m的平台面域。图2中箭头表示车轮位置,阴影部分为加载面域。

图2 移动荷载平台示意图
车轮给轨道的动荷载可以用一个激励力公式来表示[18]:
F(t)=A0+A1sinω1t+A2sinω2t+A3sinω3t。
(1)
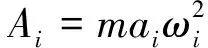
地铁B型车轴重不超过14 t,取单边车轮静载为A0=70 kN。列车簧下质量取为750 kg,借助英国轨道不平顺管理值,取得三种附加荷载对应的波长与矢高:L1=10 m,a1=4 mm;L2=2 m,a2=0.5 mm;L3=0.28 m,a3=0.05 mm。经计算可得,第三个控制条件所产生荷载幅值最大,频率最高。在计算时,频率越高,所需时间增量步长越短,计算代价越高,这是三维模拟的弊端,所以三维模拟多用于模拟低频振动。地铁振动在近振源处以高频为主,远振源处以低频为主,高频振动衰减很快,对地表起主要作用的是低频振动。严涛等[19]在进行地铁振动三维响应模拟时,将静荷载和典型的低频正弦荷载进行叠加得到动荷载,其低频荷载频率取为20 Hz。张柯[20]将地铁荷载简化为单一频率的半正弦荷载,模拟了西安黄土地层在20 Hz以下的加载、卸载频率下的动力响应,结果表明,频率在1~15 Hz范围变化时地面振动变化较明显,15 Hz和20 Hz荷载频率下地表振动加速度幅值较接近。本次模拟也重点研究低于20 Hz的振动,且模拟荷载是以实际车速移动的,分析步长不能太短,以致高频成分不易顾及,又因第一个控制条件下荷载幅值较小,所以将第一和第三个控制条件附加于条件二。取典型圆频率为ω2,但考虑到A1、A3对振动荷载幅值有影响,所以将A2乘以一个系数λ,经计算得到λ的取值范围是5.00~7.50,则式(1)转化为:
F(t)=A0+λA2sinω2t。
(2)
西安地铁设计最高时速为80 km/h,在此车速下,λ取值为6.40,由式(2)计算得到单边轮载为F(t)=70 000+11 686sin(22.22πt) (N)。图2中荷载平台每一个加载面域面积s=2.4 m2,单个面域压强荷载为:

(3)
2.2 模拟车辆数目的确定
利用无地裂缝的整体式隧道模型,在荷载平台的第三节车辆位置施加地铁荷载,该荷载不移动,目的是确定单节车产生振动的影响范围。地铁运行产生的振动以竖直方向为主,此处提取隧道正上方测量线A各节点在加载全过程的竖直加速度幅值,测量线位置如图3所示,绘制曲线如图4所示。

图3 测量线A位置示意图

图4 测量线A竖直加速度幅值分布曲线

图5 各测量线位置示意图
从图4中可以看出,在距模型端部110m处,竖直加速度已经减到很小值,约为最大加速度的5%,此处距加载部位约70m。因此,可以确定,单节车产生的振动沿隧道纵向的影响范围不超过75m,模拟时选择4节车足以保证计算精度。
3 振动响应模拟结果分析
3.1 整体式隧道振动响应分析
模拟时,列车运行速度为80km/h,由上盘往下盘运动,共运行50m。对于穿地裂缝带的整体式隧道,主要分析振动在土层中沿横向和竖向的传播规律,并对有无地裂缝时的振动响应进行对比,以分析地裂缝对振动响应的影响。
(1)振动沿横向的传播分析
提取列车运行全过程中测量线1各节点竖直和水平加速度幅值,线1距地裂缝30m,位置如图5所示,绘制曲线如图6所示。

图6 测量线1竖直与水平加速度幅值分布曲线
从图6中可以看出,在距离隧道中心线14m范围内,竖直加速度大于水平加速度,14m以外,水平加速度略大于竖直加速度。可以说明水平振动衰减较缓。水平加速度在12~22m范围内取得最大值。
(2)振动沿竖向的传播分析
选择上盘的测量线2 和3,位置如图5所示。提取各节点竖直加速度的幅值,绘制曲线如图7所示。

(a)测量线2竖直加速度

(b)测量线3竖直加速度
从图7(a)可以看出竖直振动在由衬砌顶传至地表的过程中,振动强度逐步衰减,在距离地表4m处减幅变大,4m以下减幅约为0.132mm·s-2·m-1,4m以上减幅约为0.654mm·s-2·m-1。对比图7(a)、(b),可以看出衬砌下部一定范围内土体振动加速度要比上部大。竖向振动在由衬砌底传至下部地层过程中,11m前,减幅约为0.885mm·s-2·m-1;11m后,减幅明显变缓,约为0.164mm·s-2·m-1。说明竖向振动在经衬砌传递至下部地层的过程中振动强度先迅速衰减接着减幅有所变缓。
3.2 有无地裂缝时的振动响应对比
此处将有地裂缝和无地裂缝场地的整体式隧道-地层模型的振动响应进行对比,重点探究地裂缝附近土体的振动规律。由于竖直加速度在隧道正上方最大,选取隧道正上方测量线4,线4跨过地裂缝,向上下盘各延伸40m、24m;同时选取衬砌正下方土体测量线5,距衬砌底14.6m,向上下盘各延伸30m。选取距离隧道中心线10m的测量线6,进行水平加速度的对比,各测量线位置如图5所示。对于衬砌的振动响应,仅选取部分特殊点进行研究。
(1)土层振动响应对比
①竖向振动对比分析
提取测量线4、5各节点竖直加速度幅值,绘制曲线如图8所示。

(a)测量线4竖直加速度

(b)测量线5竖直加速度
从图8(a)可以看出,有无地裂缝时,加速度幅值的分布曲线均较平滑,不同之处是存在地裂缝时,在地裂缝左右加速度幅值跳跃很明显。单看曲线的走向,两曲线大体变化趋势相近。从曲线整体的位置来看,在离地裂缝10m以外,有地裂缝时的加速度幅值稍大于无地裂缝时。这说明在离地裂缝10m以外,地铁运行诱发的竖向振动与无地裂缝场地相比并没有出现显著的放大现象。在地裂缝处,加速度幅值从上盘的0.690mm/s2跳跃至下盘的1.083mm/s2,曲线在地裂缝左右呈现正“N”字形分布,而且下盘振动加速度较无地裂缝时大,上盘则相反。从图8(b)可以看出,在地裂缝左右12m以外,有地裂缝时的曲线位置稍高于无地裂缝时,说明地裂缝对衬砌下部距地裂缝12m以外的土体振动并无明显影响。在地裂缝位置,加速度由上盘的2.237mm/s2突降至下盘的1.510mm/s2。曲线在地裂缝左右呈现倒“N”字形分布,在距地裂缝12m范围内,上盘土体节点竖直加速度较无地裂缝时大,下盘则相反。对比图8(a)和(b)可以发现,衬砌下部测量线5处土体加速度幅值要大于地表土体。
②水平振动对比分析
提取测量线6各节点水平加速度幅值,绘制曲线如图9所示。

图9 测量线6有无地裂缝时水平加速度幅值对比
由曲线可以看出,无地裂缝时,曲线从右向左很平稳地降低,有地裂缝时的曲线在地裂缝附近出现了跳跃。在地裂缝左右14m范围以外,有无地裂缝时的曲线基本是重合的,振动的减弱与放大效果并不明显。在14m范围以内,上盘节点的加速度较无地裂缝时小,下盘则相反。曲线在地裂缝两侧呈现正“N”字形分布。
(2)衬砌振动响应对比
选取3个断面,每个断面选择拱顶、拱腰和拱底三个点。断面1距下盘端口4m,断面3距上盘端口4m,断面2位于上盘距地裂缝约2m处,各测量点位置如图10所示。将各节点在有无地裂缝时的竖直加速度幅值列于表2。
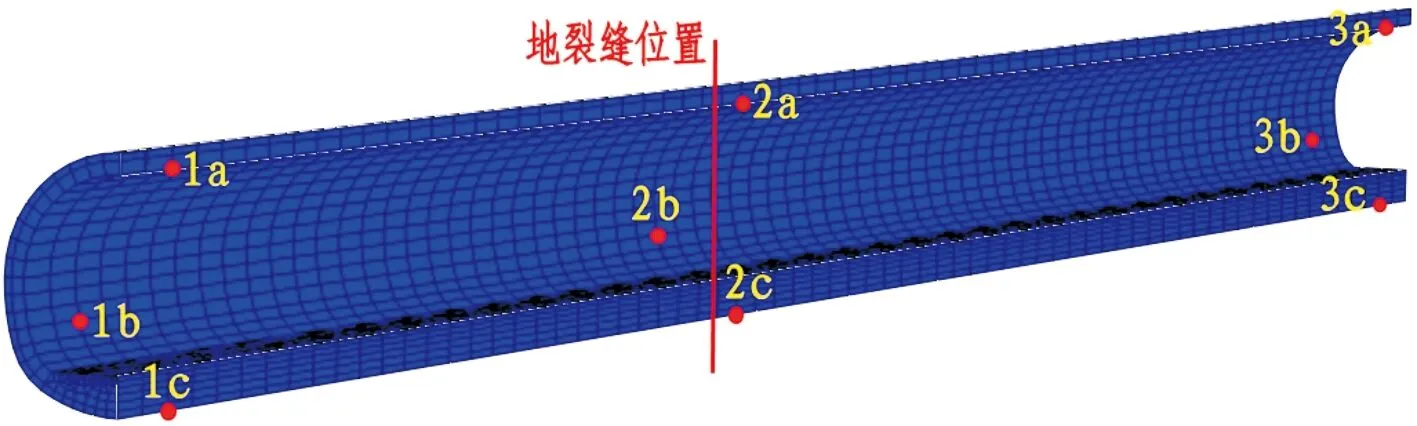
图10 衬砌各测量点位置示意图
表2 衬砌各测量点有无地裂缝时竖直加速度峰值对比

测量点竖直加速度峰值/(×10-2m/s2)有地裂缝无地裂缝断面11a0 0680 0661b0 0600 0591c0 0720 069断面22a0 3880 3852b0 7770 7672c1 4951 478断面33a0 2720 2743b0 4570 4593c0 4830 482
综合表中数据可以看出,在有无地裂缝条件下,各测量点的加速度幅值差异不是很明显。说明地裂缝的存在对衬砌结构振动的影响并不显著。从表中数据还可以发现,拱底加速度均最大,拱顶最小。
4 结论
本文基于地裂缝场地地铁动荷载作用下的隧道-地层三维动力响应,开展了数值模拟的研究,主要结论和认识如下:
(1)基于“移动荷载平台”的思想,提出了地铁动荷载的施加方法,确定了单节车辆诱发的振动沿隧道纵向的影响范围不超过75m。
(2)对地裂缝场地整体式隧道-地层的振动响应,竖直加速度在隧道正上方最大,在本次模拟工况下,水平加速度的最大值在距离隧道中心线12~22m范围内取得。振动沿横向传播过程中,水平加速度较竖直加速度衰减慢。振动在土体中沿竖向传播时,随着距衬砌距离的增大而衰减。衬砌下部一定范围内地层的振动强于上部地层。
(3)在本次模拟的参数条件下,发现地裂缝对邻近土体的振动有一定影响。在地裂缝左右约12m的范围内,土体的振动有加强现象。地裂缝的存在对衬砌结构的振动响应影响不大。有关地裂缝倾角、尺寸以及缝间不同填充物等条件对振动响应的影响有待进一步研究。
[1] 潘昌实,李德武,谢正光.北京地铁列车振动对环境影响的探讨[J].振动与冲击,1995,14(4):29-34.
[2] 张玉娥,潘昌实.地铁区间隧道列车振动响应测试与数值分析[J].石家庄铁道学院学报,1993,6(2):7-13.
[3] 刘卫丰,刘维宁,袁扬,等.地铁列车与道路车辆运行对环境的振动影响现场测试与分析[J].铁道学报, 2013,35(5):80-84.
[4] 楼梦麟,贾旭鹏,俞洁勤.地铁运行引起的地面振动实测及传播规律分析[J].防灾减灾工程学报,2009, 29(3):282-288.
[5] 钱春宇,郑建国,董霄,等.地铁运营引起的西安钟楼振动响应研究[J].桂林理工大学学报, 2012, 32(3):375-380.
[6] 刘建达,苏晓梅,陈国兴,等.地铁运行引起的地面振动分析[J].自然灾害学报,2007,16(5):148-154.
[7] 宫全美,徐勇,周顺华.地铁运行荷载引起的隧道地基土动力响应分析[J].中国铁道科学,2005,26(5):47-50.
[8] 白冰,李春峰.地铁列车振动作用下近距离平行隧道的弹塑性动力响应[J].岩土力学,2009,30(1):123-127.
[9] 单涛涛,楼梦麟,蒋通,等.地铁诱发地面振动传播衰减特性分析[J].防灾减灾工程学报,2013,33(4): 461-467.
[10]AndersenL,JonesCJC.Coupledboundaryandfiniteelementanalysisofvibrationfromrailwaytunnels-acomparisonoftwoandthreedimensionalmodels[J].JournalofSoundandVibration,2006,293(3): 611-625.
[11]张鹤年,阳建强,孙广俊,等.地铁运行诱发的环境振动数值模拟与模型预测[J].东南大学学报:自然科学版,2012,42(5):988-993.
[12]孟昭博.西安钟楼的交通振动响应分析及评估[D].西安:西安建筑科技大学,2009.
[13]黄强兵. 地裂缝对地铁隧道的影响机制及病害控制研究[D].西安:长安大学,2009.
[14]LysmerJ,KuhlemeyerRL.Finitedynamicmodelforinfinitemedia[J].JournaloftheEngineeringMechanicsDivision,ASCE,1969,95(4):859-877.
[15]骆亚生.中国典型黄土动力特性及其参数的试验分析[D].西安:西安理工大学,2000.
[16]李才志,张春华.移动荷载在ABAQUS中的模拟研究[J].水运工程,2012,(9):61-64.
[17]冯悦.列车荷载下高温冻土场地路基的动力反应分析[D].哈尔滨:哈尔滨工业大学,2012.
[18]潘昌实,PandeGN.黄土隧道列车动荷载响应有限元初步数定分析研究[J].土木工程学报,1984,17(4):19-26.
[19]严涛,肖新标,金学松,等.地铁列车运行引起的环境振动三维数值分析[J].铁道建筑,2010,(7):67-69.
[20]张柯.地铁行车荷载作用下黄土地层的振动响应和沉降[D].西安:西安建筑科技大学,2011.
《灾害学》继续成为中国科学引文数据库(CSCD)来源期刊
《灾害学》编辑部2015年5月收到中国科学院文献情报中心、中国科学引文数据库的收录证书,依据文献计量学的理论和方法,通过定量与定性相结合的综合评审,《灾害学》杂志继续被收录为中国科学引文数据库(CSCD)来源期刊(有效期2015-2016年)。
《灾害学》编辑部
There-dimensionalDynamicResponseofMetroTunnelandStratumDuetoSubwayMovingLoadsinGroundFissureArea
Yang Mi, Men Yuming and Jia Pengjuan
(SchoolofGeologyEngineeringandGeomatics,Chang’anUniversity,Xi’an710054,China)
InordertoinvestigatethedynamicresponsefeaturesofthetunnelandthestratuminXi’angroundfissuresiteunderthesubwaydynamicloads,thethree-dimensionalsubwayvibrationresponsenumericalsimulationmethodisproposedbasedonABAQUSandthemethodtorealizesubwaymovingloadsisgiven.Thevibrationresponsefeaturesofintegraltunnelandthepropagationlawsofthesubwayvibrationingroundfissureareaaresummarizedthroughthefiniteelementcalculation.Then,thevibrationresponseingroundfissureareaiscontrastedwiththatinnon-groundfissurearea,andtheimpactofgroundfissureonvibrationresponseisanalyzed.Calculationresultsshowthatthelongitudinalimpactrangeofthevibrationinducedbyasinglevehicleisnotmorethan75meters.Theverticalvibrationplaysaleadingroleinthevibrationinducedbysubwaytrain,andthehorizontalvibrationattenuatesmoreslowlywhenthevibrationpropagatesalongthetransversedirection.Inthissimulationcondition,thegroundfissurehasagreatimpactonthevibrationofsoilintherangeof12meters,andhasnosignificantinfluenceontheliningstructure.
groundfissure;integraltunnel;subwayloads;dynamicresponse;numericalsimulation;Xi’an
2014-12-02
2015-01-16
国家自然科学基金项目(41172257)
杨觅(1988-),男,湖北荆州人,博士研究生,主要从事地下建筑安全与地质灾害治理方面研究.E-mail:844144139@qq.com
TU435;U260.17;X4
A
1000-811X(2015)03-0061-06
10.3969/j.issn.1000-811X.2015.03.012
杨觅,门玉明,贾朋娟. 地铁动荷载作用下隧道-地裂缝-地层的三维动力响应[J].灾害学, 2015,30(3):061-066. [Yang Mi, Men Yuming and Jia Pengjuan. There-dimensional Dynamic Response of Metro Tunnel and Stratum Due to Subway Moving Loads in Ground Fissure Area[J].Journal of Catastrophology, 2015,30(3):061-066.]

