毛化连接的细观力学分析

刘湘云，陈普会，马 维，王西昌

(1.南京航空航天大学机械结构力学及控制国家重点实验室，江苏南京 210016)(2.沈阳飞机设计研究所，辽宁沈阳 110035)(3.北京航空制造工程研究所，北京 100024)

复合材料-金属毛化连接与传统的连接不同，它采用电子束毛化技术进行连接［1-2］，既能够充分发挥复合材料的整体性能，避免开孔引起的应力集中问题，又能够传递较大的载荷。

电子束毛化技术可以根据需要在金属材料表面定制不同形貌(如几何形状、尺寸大小、倾斜角度、分布密度等)的毛刺。毛化连接是利用电子束毛化技术对金属件进行表面处理，毛化成所需要的表面形貌，然后将金属件与复合材料件通过加温加压共固化得到接头。

英国焊接研究所进行了毛化接头与传统胶接接头的对比试验［3］，试验结果表明，毛化接头能够承受更大的载荷，且在接头失效之前能够吸收更多的能量。Guild、Tu等采用二维代表体积元(RVE)［4］和三维子模型分析了毛刺高度、形状以及毛刺密度、分布对复合材料区域应力集中大小及位置的影响［5］。曹正华等将电子束毛化表面处理与传统表面处理进行了对比试验，分析了毛化接头的失效机理［6］。总体来说，目前国内外关于毛化接头的研究非常少，仍处于探索阶段。

本文采用细观力学分析方法，通过建立毛化接头毛化区域周期性单胞的三维有限元分析模型，提出一种预测单胞弹性模量的方法，用于分析毛化参数对毛化区域单胞弹性力学性能的影响，为毛化参数的选取提供依据。

1 毛化连接细观有限元分析

1.1 细观有限元建模

毛化接头包括1～3号共3个组件，如图1所示，图中单位为mm。毛化接头是在1号金属件的搭接面上制出毛刺，与2号复合材料件铺层压实后加温加压共固化成形。毛刺为底边长约1mm、厚度约为0.2mm的直角三角形，相邻两列毛刺交错排列。金属表面形貌及毛化区域剖面如图2，3所示。

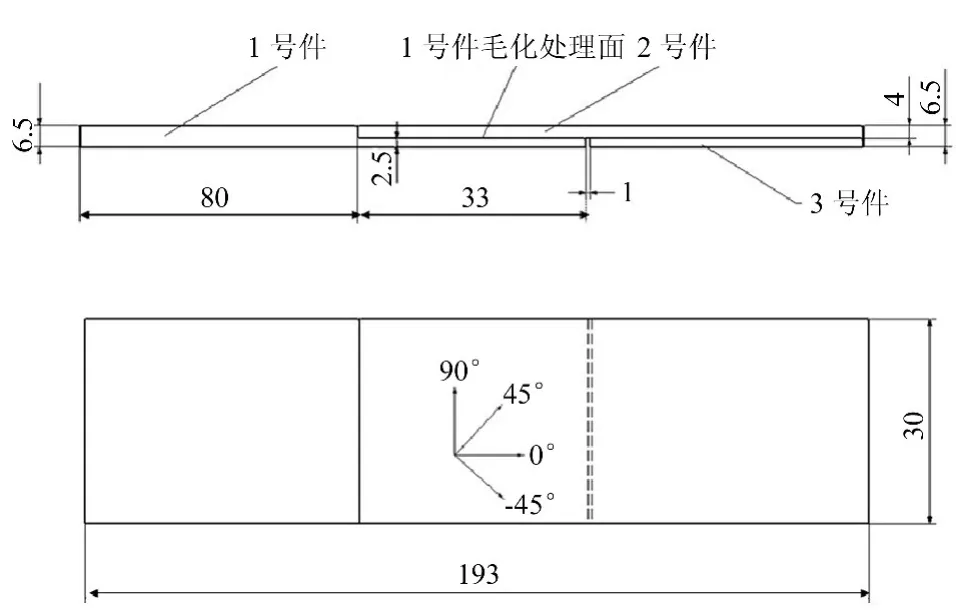
图1 毛化接头的几何构型与尺寸

图2 金属表面电子束毛化

图3 毛化接头剖面

1号件材料为TC4锻件，2号件、3号件材料为T300/BA9916复合材料，单层厚度为0.125mm。接头毛化参数见表1，TC4锻件基本性能见表2，复合材料单层性能见表3，2号件铺层顺序见表4。

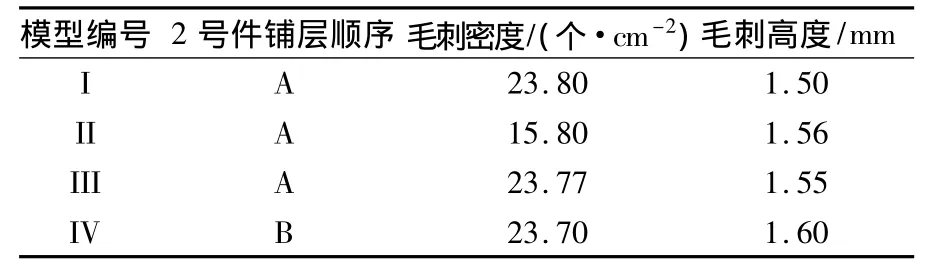
表1 接头毛化参数

表2 TC4材料基本性能

表3 T300/BA9916复合材料的基本性能

表4 复合材料件铺层顺序

由于金属表面的毛刺近似呈周期性分布，因此毛刺层可以看成是由许多细观结构相同的单胞按照周期排布堆砌而成。单胞的选取需满足细观结构上的周期性和连续性，边界要满足位移和应力的周期性和连续性。单胞中的细观位移和细观应力都是类似的，可以用一个单胞的平均性质代表整块毛刺层的宏观性质，将毛刺层等效成一种均匀材料［7］。

单胞周期性边界条件［8-9］的统一写法如式(1)，表示单胞相对的平行表面在变形之后仍然保持平行。

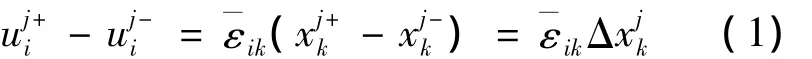
式中:指数j+表示沿着xj轴正向;j－表示沿着xj轴负向。

上述边界条件所包含的应变可认为是单胞的独立自由度，集中力可以加在这些自由度上，由能量等效得到应力。假设单胞x方向长为L，如果集中力Fx加在单胞自由度上，同时其他自由度无约束，那么该力所做的功为:

单胞的应变能可用宏观应力和应变来表示:

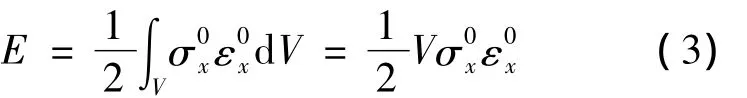
式中:V为单胞体积。由外力功与应变能相等可得到Fx与的关系，从而得到等效材料参数。对于 I号接头，其单胞模型取 4.10mm×2.05mm×1.50mm的六面体，包含2个毛刺，如图4所示。假设毛刺与复合材料之间的界面为理想界面，即在受力过程中，界面不发生分离、嵌入或相对滑移。复合材料和金属毛刺都采用四面体单元C3D4，单胞采用“equation”约束施加周期性边界条件。

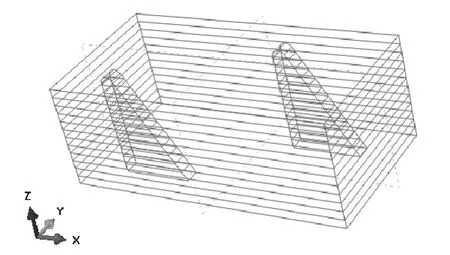
图4 毛刺层单胞模型

1.2 毛刺层的弹性模量

约束单胞的刚体位移，在x方向施加位移载荷，图5所示为单胞x方向应力云图。

x方向应变为4.88×10-3时，单胞所受集中力为1.08kN，由此计算可得单胞的平均模量即毛刺层的弹性模量及泊松比为:E1=71.84GPa，ν12=0.48，ν13=0.24。在 y和 z方向分别单独施加位移载荷，可得毛刺层的其余弹性模量及泊松比为:E2=33.41GPa，ν23=0.35，E3=13.00GPa。

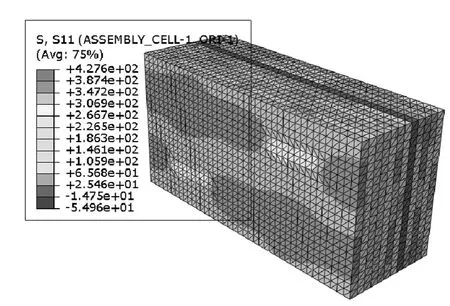
图5 单胞x方向应力分布

约束刚体位移，在垂直于xy平面的4个面上分别施加100MPa均布面载荷，剪应变为4.91×10-3，则剪切模量为G12=20.38GPa。同样可得到另外 2个剪切模量:G13=4.43GPa，G23=3.66GPa。

计算所得各模型毛刺层性能汇总于表5。分析结果表明:相同铺层顺序下，毛刺高度较小时，面内弹性模量越大，剪切模量越小;复合材料铺层角度90°所占比例越大，沿拉伸方向弹性模量越低，垂直于拉伸方向的弹性模量越高。

表5 毛刺层的平均刚度

2 结束语

文中提出的预测复合材料-金属毛化接头毛化区域等效弹性模量的细观有限元模型，为毛化接头参数的选取提供技术支持。

本文研究了毛化参数(包括毛刺高度及分布密度、复合材料层合板铺层顺序)对毛化区域力学性能的影响，研究表明，通过调整毛刺高度及分布密度，增大复合材料0°层比例，可以获得较强的连接属性。本文仅研究了毛化区域的弹性性能，其破坏机理及失效模式还需进一步研究。

［1］ Dance B G I，Kellar E J C.Workpiece structure modification:U.S.，Patent 7，667，158［P］.2010-02-23.

［2］ Tu W，Guild F J，Hogg PJ.Comeld joints:a novel technique for bonding composites and metal［J］.Rare Metal Materials and Engineering，2009，38:134-141.

［3］ Dance B G I.Surface modification:U.S.，Patent 6，670，571［P］.2003-12-30.

［4］ Sun C T，Vaidya R S.Prediction of composite properties from a representative volume element［J］.Composites Science and Technology，1996，56(2):171-179.

［5］ Tu W，Wen P，Guild F J.Optimisation of the protrusion geometry in comeld joints［J］.Composites Science and Technology，2011，71(6):868-876.

［6］ 阳灿，曹正华，胡孝才.表面处理工艺对复合材料与金属连接性能的影响［J］.航空制造技术，2009(增刊1):136-138.

［7］ Li S，Wongsto A.Unit cells for micromechanical analyses of particle-reinforced composites［J］.Mechanics of Materials，2004，36(7):543-572.

［8］ Xia Z，Zhang Y，Ellyin F.A unified periodical boundary conditions for representative volume elements of composites and applications［J］.International Journal of Solids and Structures，2003，40(8):1907-1921.

［9］ Weissenbek E，Böhm H J，Rammerstorfer F G.Micromechanical investigations of arrangement effects in particle reinforced metal matrix composites［J］.Computational Materials Science，1994，3(2):263-278.