EMD结合RBF神经网络新混合模型及股指期货价格预测

史文静　高岩

摘要 中国近4年才成立的股指期货市场价格呈现出非平稳、非线性的信号特征， 传统的预测方法无法对长相关序列进行精确预测. 将EMD与RBF相结合， 建立了一种新的预测方法对我国股指期货日结算价格进行预测. 结果显示本模型将原本具有长相关性质的原始序列分解为若干个短相关性质的不同频带， 解决了原始序列随机性强， 以及因相邻频带的干扰而造成的系统动力信息反映不足的缺陷； 并与其他预测模型进行比较， 显示出较高的预测精度.

关键词 EMD； RBF神经网络； 股指期货

中图分类号 F830 文献标识码 A

AbstractOnly in the past four years did China set up the stock index futures market displaying the nonstable and nonlinear signal features. The traditional estimation methods cannot make accurate estimation of longrelevant sequence. Combining EMD with RBF， we have created a new method of estimation to predict the daily settlement price for stock index futures. The result shows that this model has separated the original sequence with longrelevance features into several shortrelevance frequency bands， making up for the shortage of system power information caused by the serious randomness of the original sequence and the interruptions from nearby frequency bands. It is also compared with other estimation models to display a relatively high degree of accuracy.

Key wordsEmpirical Mode Decomposition； RBF； stock index futures

1引言

通过价格信号对资源进行合理配置是市场经济条件下经济发展的主要手段. 因此期货市场应运而生， 为国民经济的发展创造了多种风险管理工具， 保证国民经济的运行. FLOROS通过对欧美金融市场的研究， 表明股指期货保证了股市正常健全的发展[1]. 由此可见， 不仅应从资本市场发展和体制转换的大系统来考虑股指期货的必要性， 更应该从目前股指期货市场隐含的需求和深层的矛盾来研究股指期货市场.

中国沪深300股指期货是2010年， 由中国金融期货交易发行， 将沪深300指数作为标的物， 为长期投资者提供风险管理服务的一种新生金融商品. 我国股指期货经过四年的成长， 市场制度逐步完善，但对其的研究却不够成熟. 而股指期货价格预测作为提高金融市场风险防范能力和增强投资组合收益的有效途径之一， 逐渐引起学术界的重视， 探究和开发针对当前股指期货市场价格波动特征下的价格预测方法是具有现实意义的研究课题.

就目前对金融市场预测方法而言， 常见的预测方法有自回归滑动平均模型（AutoRegressive and Moving Average Model， ARMA模型）、灰色预测模型、曲线拟合、BP 神经网络模型、支持向量机（Support Vector Machine， SVM）以及小波神经网络预测模型等.

虽然在短期内这些传统的模型预测方法显示出良好的效果， 但都不能有效解释股指期货波动的内在驱动力和经济含义， 也不能准确地预测非平稳时间序列. 基于模型阶数的ARMA模型因其阶数不容易确定造成预测精度不高[2，3]. 当数据灰度很大或者对系统内在机理理解不清除的情况下， 运用灰色预测模型会造成很大的误差[4]. BP神经网络算法一般都是根据经验来选择合适的网络结构，这就使得网络的逼近和训练能力具有不确定性，很难确定合适的网络结构[5，6]. 支持向量机的预测结果具有滞后性、拐点处误差较大的缺陷， 影响预测精度[7]. 小波神经网络变换的有效性是由分解层数和小波基的选择决定， 不能确保最佳的信号分解[8].

股指期货价格是典型非平稳、非线性时间序列， 具有长相关性， 而传统预测方法并没有充分考虑到序列的随机性、周期性和趋势性的特点， 只是针对整个时间序列进行预测， 预测精度不高. 为了提高非平稳、非线性时间序列的预测精度， 本文采用经验模态分解（Empirical Mode Decomposition， EMD）在处理非线性、非平稳信号方面的优势， 将股指期货原本具有长相关性质的原始序列分解为若干个适于预测的短相关性质的不同频带， 探究其波动的结构性特征， 为认识股指期货的波动提供新思路， 提出了基于EMDRBF的股指期货价格新预测模型.

2方法基础

N. E. Huang等人提出的了一种适用于非线性、非平稳信号的新型自适应信号时频处理方法—经验模态分解（EMD）[9]. EMD方法根据数据自身的时间尺度特征将信号中不同时间尺度的波动逐级分解为一个代表原始信号总体趋势的剩余分量和有限个本征模函数（Intrinsic Mode Function， IMF）， 各IMF分量包含了原始信号不同时频特征[10]. 该方法的变换并不是基于事先设定好的基函数， 而是对数据本身的一种分解， 具有直接、后验、直观和自适应的优点， 是对以线性和平稳假设为基础的小波基和傅立叶分解的突破.

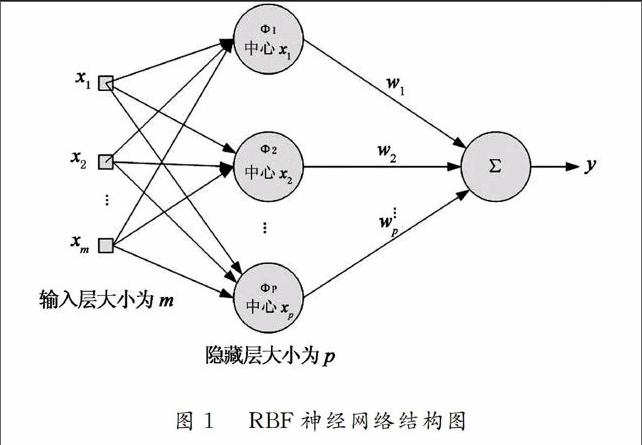
Moody和Darken首先将RBF（RadialBasis Function， RBF）应用于神经网络设计[11]. RBF网络的基本思想是将隐含层空间由径向基函数（RBF）作为隐单元的“基”来构成， 变换输入矢量， 将原本低维的模式输入数据变换到高维空间内， 输出层再将隐单元的输出加权求和得到结果. 其结构图如图1所示.

一般采用线性激励函数作为输入和输出神经元函数. 径向基函数地快速衰减性使得RBF网络具有全局逼近和超速学习的优点， 学习方式也比BP神经网络更丰富， 且可以调节网络结构的众多参数[12].

3一种新的预测模型设计

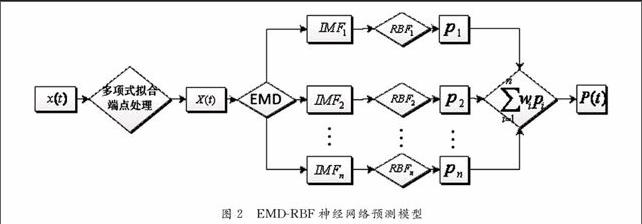
将EMD与RBF神经网络相结合的新模型来改善无法对长相关序列精确预测的缺陷， 提高预测模型的精度， 为预测股指期货市场价格提供新的思路和借鉴. EMDRBF神经网络预测模型的基本思想如下：

1）数据预处理； 在运用EMDRBF新模型对原始时间序列进行初始预测会产生一定的偏差， 这些偏差会使最后的预测结果与实际结果的误差增大，影响模型的预测精度. 因此采用多项式拟合算法对原数据端点做处理， 防止原序列极值端点发生发散现象并“污染”整个结果[13]. 处理后的数据序列为{Xt，t=1，2，…，m}.

4沪深300股指期货价格预测

4.1数据样本选择

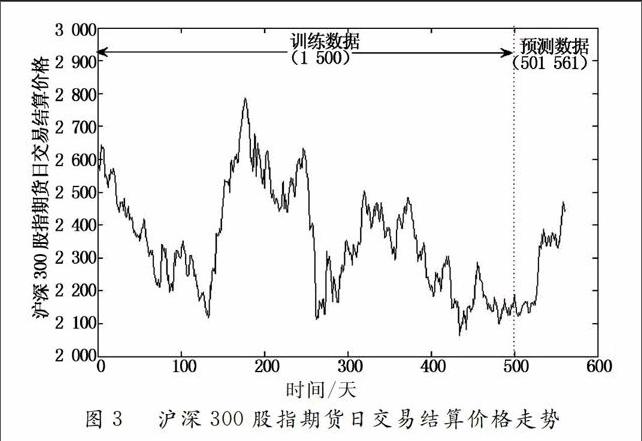
选取中国沪深300股指期货2012～2014年两年的日交易结算价格， 共计561个样本数据. 图3为沪深300主连合约日交易结算价格曲线. 将区间（1，500）的数据作为建立模型的训练数据， 区间（501，561）的数据作为最后与预测数据进行比对的原数据. 本文用MATLAB R2010处理数据.

4.2评价准则

为了检验预测效果， 对测量误差进行测量， 选用平均绝对误差MAE（Mean Absolute Error）、均方根误差RMSE（Rootmeansquare Error）两个指标衡量预测误差的大小； 方向对称（Directional Symmetry ，DS）显示正确预测目标值方向的次数与预测样本容量的百分比， 因此可以作为各模型对股指期货方向走势预测性能的评价准则. 设Pi为模型预测值， Ri为实际值， 则MAE、MSE和DS的表达式分别为

4.3EMDRBF神经网络模型预测

首先用多项式拟合算法对原数据端点做处理，防止原序列极值端点发生发散现象并“污染”整个结果； 然后采用EMD分解方法， 把股指期货序列分解为具有不同时频特征的本征模函数IMF， 分解结果为图4所示的6个IMF分量和一个剩余分量； 使用时间序列过去3天历史结算价格预测未来一天结算价格， 对各个IMF分量及剩余分量先处理得到各自的训练样本和训练目标， 其中训练样本为一个3行500列的矩阵， 训练目标为一个1行500列的向量， 将这两类训练样本归一化为0～1之间来提高收敛速度； 再对各IMF分量建立相应的RBF神经网络预测模型进行预测，得到不同频带未来60天的预测值， 将各频带的预测值等权叠加， 在反归一化得到股指期货未来60天最终的预测值， 如图5所示. 图6为预测值与实际值的误差波动.

为了检测EMDRBF新模型的预测能力， 运用了GARCH、ARIMA和RBF神经网络模型对沪深300股指期货的日交易结算价格进行了训练与预测，与本模型的预测结果进行比较， 如表1所示.

5结论

如何提高非平稳、非线性信号的预测精度一直是研究以来的重要课题. 沪深300股指期货序列是典型的非平稳、非线性时间序列. 而传统的预测方法并没有充分考虑到序列的随机性、周期性和趋势性的特点， 只是针对整个时间序列进行预测， 预测精度不高. 本文提出的模型将原长相关序列转化为若干个便于预测的短相关时间序列进行预测， 提高了预测精度. 首先对原始价格序列进行EMD分解，再对其分量进行RBF预测， 最后将各预测结果等权求和得到最终预测结果， 对沪深300股指期货日结算价格进行实证分析， 预测结果如下

1）对原数据端点用多项式拟合算法做了处理，防止原序列极值端点出现发散现象并“污染”整个结果.

2）将EMD方法引入到金融预测上来， 建立了EMDRBF神经网络预测模型， 使原始序列信号中的信息通过各本征模函数IMF得以充分体现，将原本具有长相关性质的原始序列分解为若干个短相关性质的不同频带， 解决了原始序列随机性强，以及因相邻频带的干扰而造成的系统动力信息反映不足的缺陷， 丰富了预测数值的经济含义.

3）对沪深300股指期货日交易结算价格进行实证分析， 结果表明EMDRBF神经网络新预测模型充分考虑了股指期货价格波动的周期性、趋势性和随机性特征， 并与常用的金融领域的预测方法进行比较， 提高了金融市场预测方法的预测精度.

对于中国来讲， 股指期货市场是一个涉及社会、经济、科学技术、政治等众多因素的复杂金融系统. 近四年引入的股指期货， 不仅为股票现货市场提供了风险对冲的方法， 更能帮助机构投资者回避股市系统风险. 因此， 对股指期货价格的预测分析是一项非常重要的任务， 提高对股票市场的风险防范能力有着重要的意义. 本文研究提出的EMDRBF神经网络新预测模型针对目前股指期货市场的属性和特征， 可以为我国未来股指期货市场的价格预测提供新的思路和方法.

参考文献

[1]C FLOROS， R KIZYS， C PIERDZIOCH. Financial crises， the decouplingrecoupling hypothesis， and the risk premium on the Greek stock index futures[J]. International Review of Financial Analysis， 2013， 28（c）： 166-173.

[2]王志坚， 王斌会. ARMA模型的稳健识别及实证分析[J]. 统计与决策， 2014，405（9）： 168-171.

[3]罗永恒. 基于ARMA 模型的中国农产品价格的分析与预警[J]. 经济数学， 2013，30（1）： 96-99.

[3]陈珂， 邹权. 融入时间关联因子曲线拟合的交通流异常挖掘方法[J]. 计算机工程与设计， 2013， 34（7）： 2561-2565.

[4]窦玉丹， 袁永博， 张明媛. 基于粗糙遗传BP网络的震害损失评估模型研究[J]. 工程管理学报. 2010， 24（01）： 29-32.

[5]洪月华. 一种基于蚁群算法与粗糙集的混合BP神经网络[J]. 微电子学与计算机， 2014， 31（4）： 156-159.

[6]姚潇， 余乐安. 模糊近似支持向量机模型及其在信用风险评估中的应用[J]. 系统工程理论与实践， 2012， 32（3）： 549-554.

[7]贠晓哲， 赵松. 原油期货价格预测方法的研究基于多分辨分析小波神经网络理论[J]. 价格理论与实践， 2013，346（4）： 79-80.

[8]N E HUANG， Z SHEN， S R LONG， et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal Society A： Mathematical， Physical and Engineering Sciences， 1998（1971）： 903-995.

[9]谢晓阳， 乔新勇， 刘健敏. 柴油机工作不均匀性的振动检测方法[J]. 噪声与振动控制， 2013， 33（3）： 79-83.

[10]G RILLING， P FLANDRIN， P GONCALVES. On empirical mode decomposition and its algorithms[C]// IEEE-Eurasip Workshop on Nonlinear Signal and Image processing NSIp-03， Grado（I）， 2003.

[11]陆宁， 周建中， 何耀耀. 粒子群优化的神经网络模型在短期负荷预测中的应用[J].电力系统保护与控制， 2010， 38（12）： 65-68.

[12]卓金武， 魏永生， 秦健， 李必文. MATLAB在数学建模中的应用[M]. 北京：北京航空航天大学出版社， 2011.

[13]刘慧婷， 倪志伟， 李建洋. 经验模态分解方法及其实现[J]. 计算机工程与应用，2006，42（32）： 44-47.

[14]Qian GAO， Guangxia LI， Xiang TIAN， et al. A novel traffic prediction method based on IMF[J]. Advanced Materials Research， 2012，（490）：1421-1425.

[15]C C CHUANG， S F SU， C C HSIAO. Robust support vector regression networks for function approximation with outliers[J]. IEEE Transactions on Neural Networks， 2002， 13（6）： 1322-1330.

[16]Wei WANG， Hong ZHAO. A novel hybrid intelligent model for financial time series forecasting and its application[C]// Proceedings of the 2nd International Conference on Business Intelligence and Financial Engineering， 2009： 279-282.