主/子惯导标定中挠曲变形的ARMA补偿方法
周大旺,赵国荣,伍国胜
(1.海军航空工程学院 控制工程系,山东 烟台 264001;2.91697部队,山东 青岛 266405)
【信息科学与控制工程】
主/子惯导标定中挠曲变形的ARMA补偿方法
周大旺1,赵国荣1,伍国胜2
(1.海军航空工程学院 控制工程系,山东 烟台 264001;2.91697部队,山东 青岛 266405)
针对舰上主/子惯导标定中挠曲变形建模补偿问题,提出一种基于ARMA的建模方法;首先利用ARMA模型对挠曲变形进行建模,建模中模型辨识数据序列来自子惯导输出差分数据,而模型辨识方法为条件最小二乘参数估计方法,在模型定阶中使用AIC准则,对模型检验采用χ2检验法;然后基于该模型使用“速度+姿态+角速度”匹配方法为主/子惯导标定设计综合补偿滤波器,滤波器设计中将挠曲模型扩展到系统状态中;最后进行仿真研究,仿真结果说明该建模方法是有效的。
惯性导航;挠曲变形;在线标定;ARMA
惯性导航被广泛应用于各种武器设备中,然而惯导系统由于自身及外界等多种原因,使用一段时间后需要对惯性仪表的误差参数重新标定[1-2]。传统的定期标定方法需要返回基地进行,但是当舰艇远航则无法返回基地重新标定。因此,有在舰艇上完成一定条件下标定的需求。在舰艇环境下,中、低精度的子惯导(Slave Inertial Navigation System,SINS)有希望利用舰船主惯导系统(Master Inertial Navigation Systems,MINS)提供的基准信息完成一定条件下标定的工作。然而,在利用主惯导基准信息过程中遇到的难题是如何保证获得高精度的基准信息。在舰上,由于激励只有舰船摇摆的特点,主/子惯导之间的匹配方法一般选择“速度+姿态”或者“速度+角速度”[3-7]。但是,在这两种匹配模式下对姿态信息要求很高,必须补偿对姿态有重要影响的挠曲变形干扰因素。如何补偿这些误差成为一个重要待解决问题。
文献[6]建立3阶Gauss-Markov随机模型,并且将挠曲变形扩展为系统状态,对于挠曲变形引起的动态杆臂等也建模为随机过程,由此引起的问题是滤波器维数非常高,另外它的随机模型参数是离线数据处理获得的,是否适用实际存在问题。文献最后提出次优方法,将挠曲当成噪声处理,以牺牲精度为代价。文献[7]在文献[6]基础上将挠曲变形分为准静态挠曲和高频挠曲,分别建模为3阶Gauss-Markov随机模型,针对计算量大问题,提出预滤波技术,并且直接将挠曲当成噪声处理。文献[8-9]针对舰艇上挠曲变形特点,将挠曲变形大的y轴分量从整个系统中删除,而忽略其他轴的挠曲变形,对挠曲变形采用回避态度。文献[14]针对挠曲变形、振动等时间相关噪声,将它们处理为有色噪声,并用Gauss-Markov过程来建模,然后修改Kalman滤波器的更新公式。文献[15]针对舰艇上的挠曲变形建立二阶Gauss-Markov模形,利用相关因子法论证了用子惯导测量数据的差分构造的序列与挠曲变形序列是相似的,然后利用自相关函数法求出挠曲变形模型的参数。文献[16]利用激光测量数据来获取挠曲变形随机过程序列,并且利用最小二乘方法来辨识模型参数。文献[17]使用主/子惯导的测量数据差值作为挠曲变形建模的随机过程序列,这种处理方法是否得当还需进一步分析,毕竟主/子惯导的测量数据差中包含的误差很多,像失准角引起的误差绝对不应该忽略。文献[18]则将挠曲变形处理为白噪声,通过从滤波器的方法来对其进行处理。
综合上述文献发现,将挠曲变形处理为噪声也许对快速传递对准是合适的,但是不适合在线标定。本文针对挠曲变形进行深入分析,利用ARMA模型对其进行建模。对于挠曲变形模型参数使用子惯导输出的差分数据序列作为辨识数据序列来确定。在此基础上,利用条件最小二乘估计法和AIC定阶原则对ARMA模型进行辨识,辨识结果利用χ2检验法进行检验。在此基础上为主/子惯导在线标定设计滤波器,仿真结果验证本文方法是有效的。
1 问题描述
惯性仪表误差模型为[12]
(1)
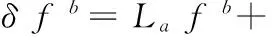
(2)
式(1)中:Kω为陀螺仪表组刻度系数和安装误差矩阵,ε为陀螺零偏误差,La为加速度计仪表组刻度系数和安装误差矩阵,▽为加速度计零偏误差,ng和na为随机噪声。
假设待标参数误差为常值误差,随机噪声为零均值不相关白噪声,则
(3)
在线标定使用的线性化误差方程为[6]
(4)

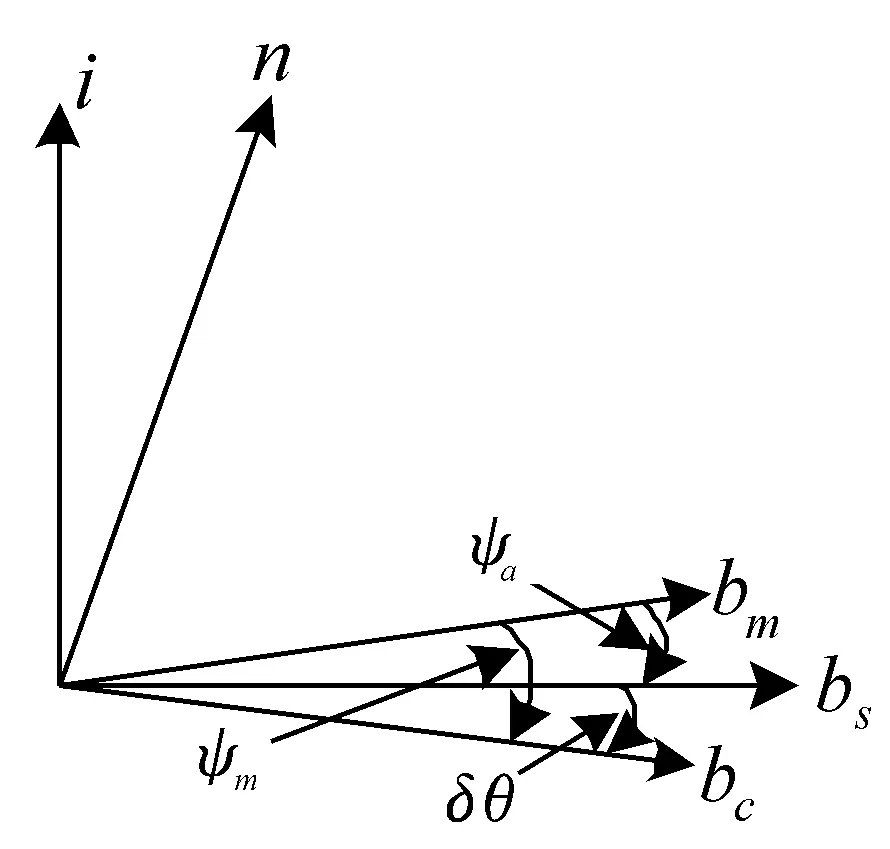
图1 坐标系关系示意图

2 基于ARMA的挠曲变形建模方法
2.1 挠曲变形模型
ARMA模型为
θk-a1θk-1-…-apθk-p=εk-b1εk-1-…-bqεk-q
(5)
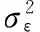
2.2 挠曲随机序列的获取
挠曲变形随机数据序列利用子惯导测量数据的差分序列来近似挠曲变形序列。通过对子惯导所测得的两个连续数据作差获取挠曲运动信息,即
(6)
2.3 条件最小二乘参数估计
设θk具有逆转形式
(7)
为了表述方便,引入后移算子D,其定义为
Dθk=θk-1,Dmθk=θk-m
(8)
则式用算子D表示可写为
(1-a1D-a2D2-…-apDp)θk=
(1-b1D-b2D2-…-bqDq)εk
(9)
εk=(1-I1D-I2D-…)θk
(10)
将式代入式,得到算子恒等式
1-a1D-a2D2-…-apDp=
(1-b1D-b2D2-…-bqDq)(1-I1D-I2D-…)
(11)
比较等式两边D的相同幂次,可得
(12)
给定A=(a1,a2,…,ap)T,B=(b1,b2,…,bq)T,由式可以递推算得逆函数{Ij,j=1,2,…},从而得到逆转形式
(13)
条件最小二乘估计方法性能指标为
(14)
其中约定:当k≤0时uk=0。而Ii由式递推算得,因为Ii是A,B的函数,故残差平方和也是A,B的函数,即
(15)

2.4 模型定阶
ARMA模型的定阶采用AIC准则。设Xt是ARMA(p,q) 序列,其中未知参数的个数是k=p+q+1个,包括自回归参数A=(a1,a2,…,ap)T和滑动平均参数B=(b1,b2,…,bq)T,则与最小平方和估计对应的对数似然函数
(16)
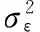
(17)
将其代入得
(18)
因此,ARMA(p,q)序列AIC定阶准则:选取p,q,使得
(19)
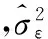
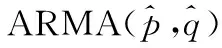
A(Xt-μ)=Bεt
(20)
这时,未知参数个数为k=p+q+2,AIC 准则:选取p,q,使得
(21)
2.5 模型χ2检验
(22)
记
(23)
则Ljung-Box 的χ2检验统计量是
(24)
检验假设:
H0:ρi=0,k≤m;H1:ρk≠0,k≤m
(25)
在H0成立时,若n充分大,χ2近似于χ2(m-r)分布,其中r是估计的模型参数个数。
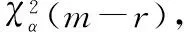
3 主/子惯导组合在线标定滤波器设计
假设安装误差参数是准确的,不需要重新标定,并且假设待标参数是固定值,则惯性仪表的方程为
(26)
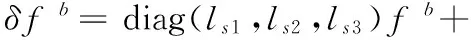
(27)
(28)

(29)
重写滤波器误差方程如下
(30)
由于挠曲变形的阶数需要辨识确定,因此,滤波器设计需要首先知道阶数,然后设计相应的状态,这里的滤波器设计是挠曲变形为二阶时的结构,其他阶数模型只要增减相应的挠曲角状态即可。
设滤波器状态为
(31)
则滤波器状态方程为
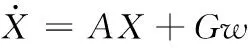
(32)
其中
A8=diag(a2x,a2y,a2z),A9=diag(a1x,a1y,a1z)
其中aij(i=1,2,j=x,y,z)表示二阶模型下的系数。
观测方程选择速度+姿态+角速度匹配模式
速度和姿态观测方程:将子惯导解算提供的速度减去主惯导提供经过刚性杆臂补偿后的速度,可以得到速度误差观测量。在误差方程中,姿态误差ψm是一个可观测量。因此这两个匹配量的观测方程为
(33)
观测矩阵:H1=[I6×6,015×15]
(34)
可以得到观测矩阵为
可以得到速度+姿态+角速度匹配模式的观测矩阵为
4 仿真研究
下面利用仿真研究对本文所提方法有效性进行验证。仿真分为两个部分,第一部分是验证挠曲变形辨识结果的有效性;第二部分分析动态杆臂补偿方法的有效性。
仿真条件设置如下:舰船系泊条件下处于摇摆状态,摇摆运动满足余弦波,其中横摇角的幅值为13°,周期10 s,纵摇角幅值5°,周期8 s,艏摇角幅值3°,周期6 s。假设主惯导的误差可以忽略,而且子惯导在进行标定前已经经过对准,对准精度为1 mrad。子惯导陀螺仪常值零偏为0.2 (°)/h,刻度系数误差为200 ppm,加速度计零偏为3×10-4g,刻度系数误差为200 ppm,刚体杆臂长度为[10,4,15]Tm。
挠曲变形仿真真值方程为
θk=0.003 5θk-1+0.07θk-2+ηk-0.04ηk-1
(36)
其中ηk的均方差取为0.000 1°。
针对式的模型进行辨识。
首先基于AIC原则,可以求得当AR各阶模型时各种情况的AIC数据,模型求解结果如表1所示。
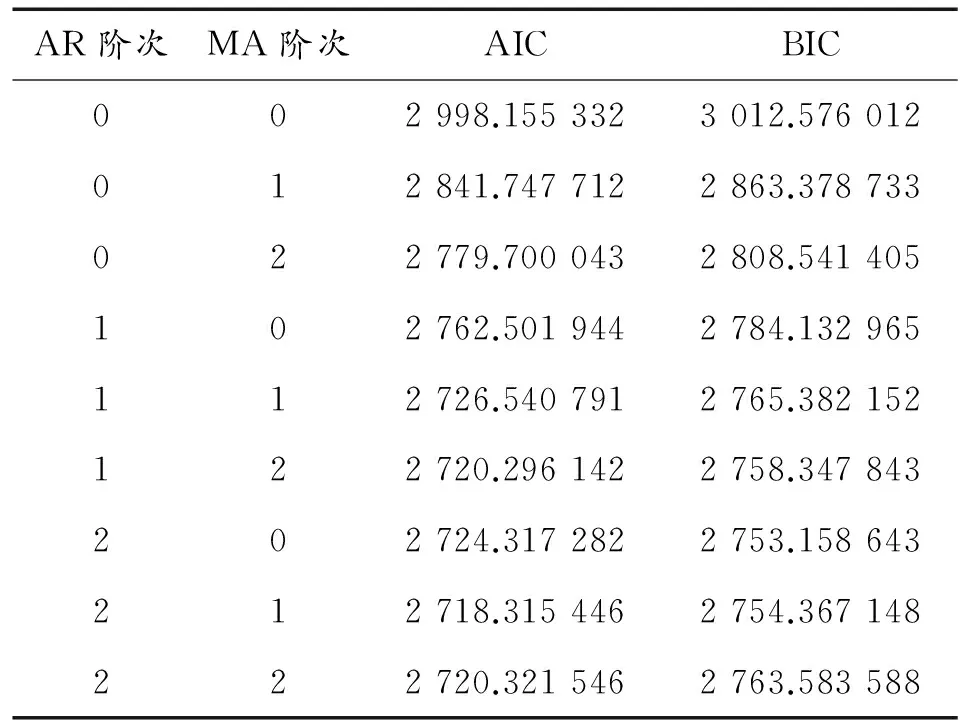
表1 模型定阶计算表
从上面结果可以确定,模型阶次为p=2,q=1。定阶结束后进行参数估计。下面是某一次估计结果确定的模型为
θk=0.003 15θk-1+0.032 9θk-2+ηk-0.041ηk-1
(37)
利用Matlab中χ2检验函数chi2gof计算结果:h=0,即接受假设H0,模型通过检验。图2是对200个数据的跟踪值与真值比较图。由图可以看出辨识模型跟踪效果良好。
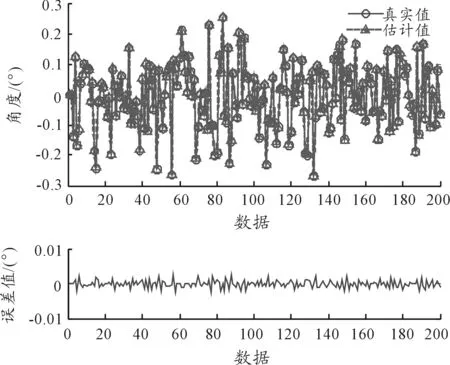
图2 辨识模型的跟踪效果
图3~图4是在速度+姿态+角速度匹配模式下,仪表零偏参数的估计结果图。图中虚线是未补偿挠曲变形,采用增大噪声水平的的结果,实线是补偿了挠曲变形的结果,可以看出经过补偿动态项后具有更高的精度。
5 结论
本文针对舰上主/子惯导标定中挠曲变形建模进行深入分析,利用ARMA模型为其建立模型,然后为主/子惯导舰上标定设计了相应的滤波器,仿真结果验证了该挠曲变形建模方法是有效的。
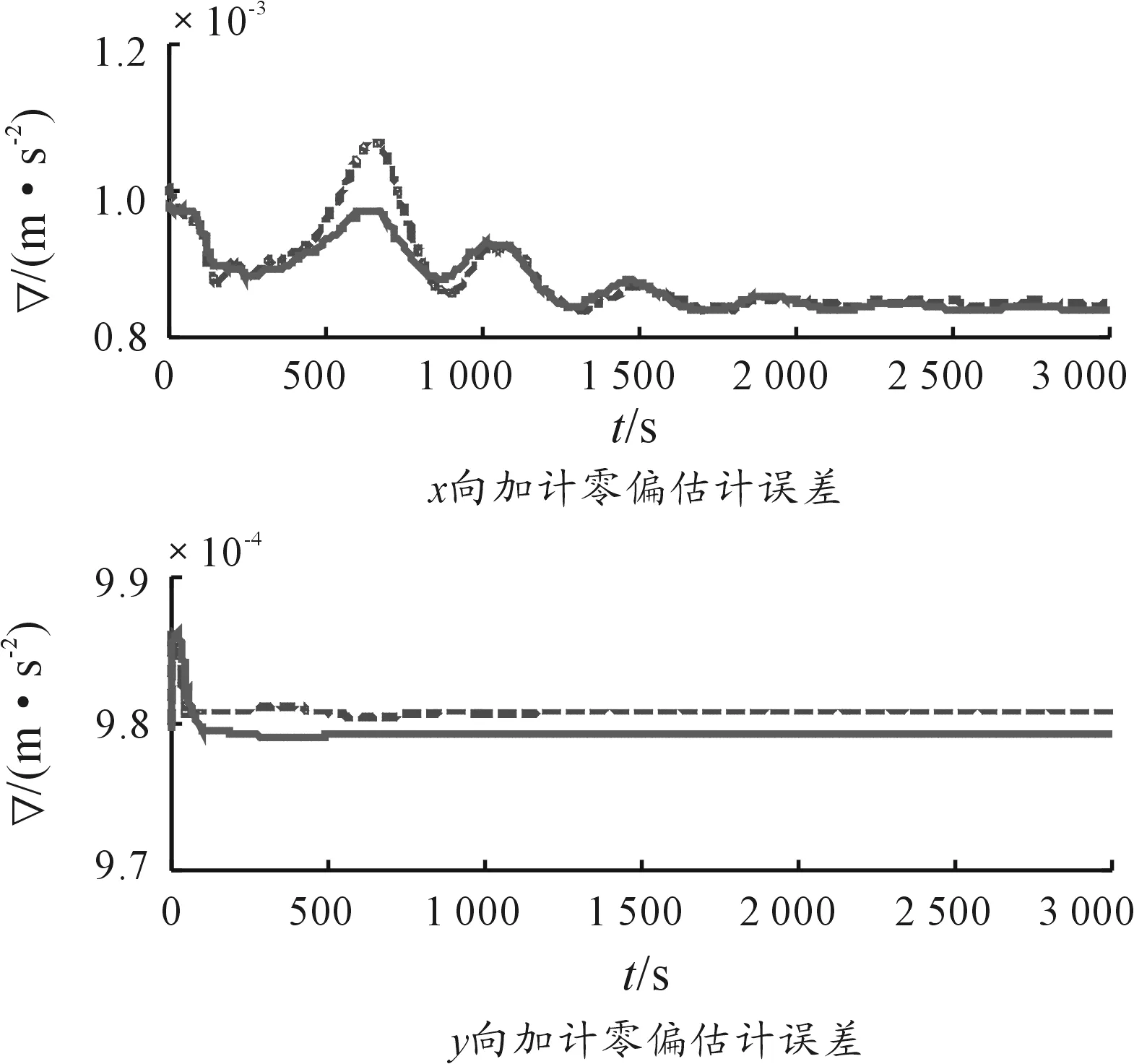
图3 加速度计零偏估计比较图
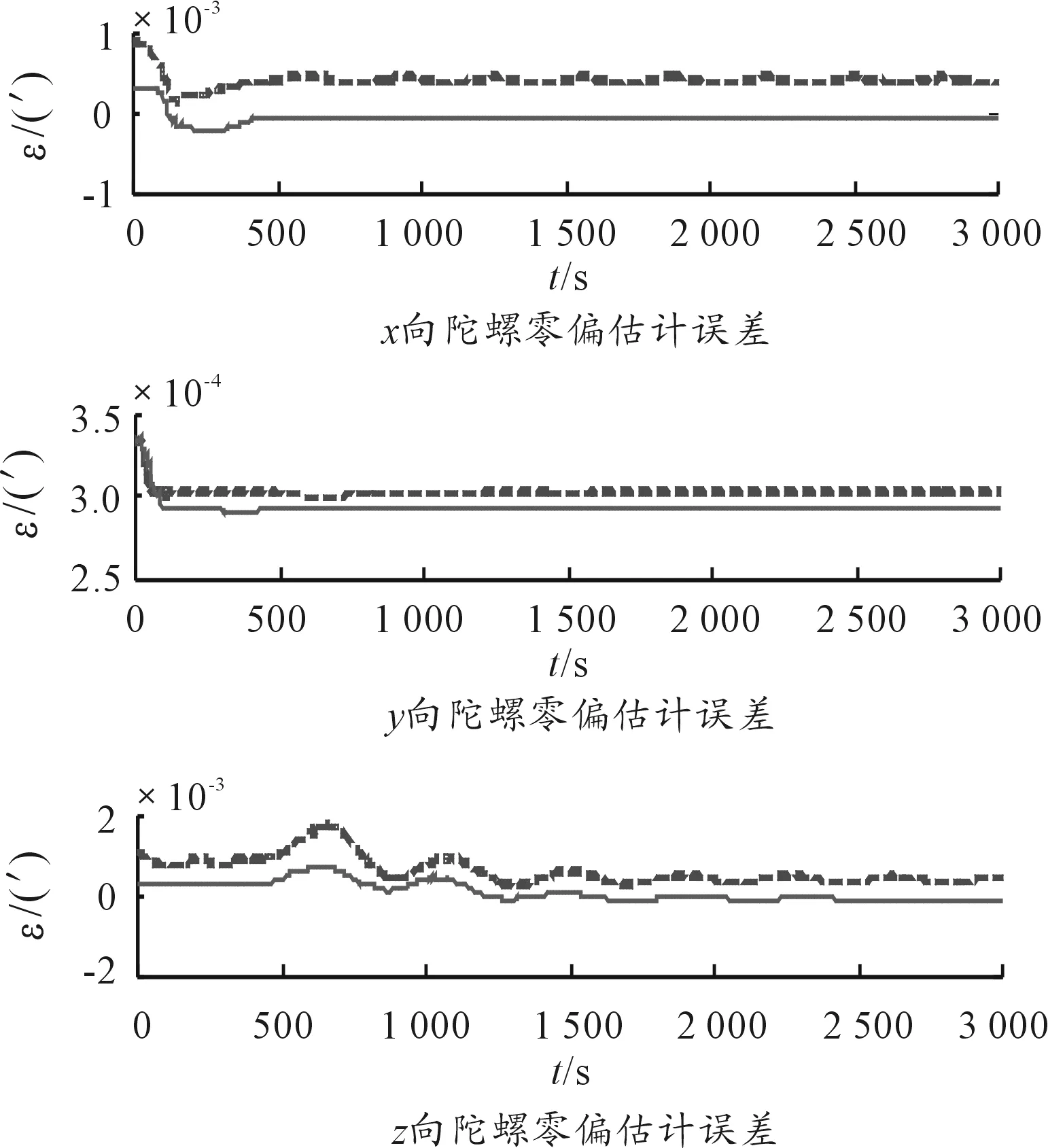
图4 陀螺仪零偏估计比较图
[1] David H Titterton,John L Weston.Strapdown inertial navigation technology(2ed edition)[M].London,United Kingdom:The Institute of Electrical Engineers,2007.
[2] Savage P G.Strapdown Analytics[M].Maple Plain,Minnesota:Strapdown Associates,Inc.,2007.
[3] Güray A,Pehlivanoglu,Yücel Ercan.Investigation of Flexure Effec on Transfer Alignment Performance[J].The Journal Of Navigation.2013,66:1-15.
[4] Chattaraj S,Mukherjee A,Chaudhurj S K.Transfer alignment problem:algorithms and design issues[J].Gyroscopy and navigation.2013,4(3):130-146.
[5] Qingwei Gao,Guorong Zhao,Xibin Wan g .Transfer A lignment eooro compensator design for flexure and lever-arm effect[C]// IEEE Conference on Industrial Electronicx and Applications.2009,21(6):1819-1822.
[6] Kain J E,Cloutier J R.Rapid transfer alignment for tactical weapon applications[R].AIAA-89-3581.
[7] Spalding K,Missouri S L.An efficient rapid transfer alignment filter[R].AIAA-92-4598.
[8] You-Chol Lim,Joon Lyou.An error compensation method for transfer alignment[C].Proceeding of IEEE Conference on Electrical and Electronic Technology.TENCON,2001,Vol2:850-855.
[9] Joon Lyou,You-Chol Lim.Transfer alignment considering measurement time delay and ship body flexure[J].Journal of mechanical science and technology,2009,23:195-203.
[10]He X F,Liu J Y.Analysis of lever arm effects in GPS and IMU integration system[J].Transact ions of Nanjing University of Aeronautics & Astronautics,2002,19(1):59264.
[11]Tedaldi D,Pretto A,Menegatti E.A robust and easy to implement method for IMU calibration without external equipments[C]//IEEE International conference on Robtics and Automation.Hong Kong.2014,3042-3049.
[12]Güray A,Pehlivanoglu,Yücel Ercan.Investigation of Flexure Effec on Transfer Alignment Performance[J].The Journal Of Navigation,2013,66:1-15.
[13]Chattaraj S,Mukherjee A,Chaudhurj S K.Transfer alignment problem:algorithms and design issues[J].Gyroscopy and navigation,2013,4(3):130-146.
[14]Jan Wendel,Jürgen Metzger;Gert Trommer.Rapid Transfer Alignment in the Presence of Time Correlated Measurement and System Noise[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit,Rhode Island,2004:1-12.
[15]孙昌跃,邓正隆.舰体挠曲运动在线建模研究[J].系统工程与电子技术,2007,29(2):243-245.
[16]解春明,赵剡,王纪南.传递对准中机翼弹性变形建模与滤波处理[J].北京航空航天大学学报,2010,36(8):931-935.
[17]陈雨,赵剡,张华强.传递对准中机翼弹性变形处理[J].火力与指挥控制,2013,38(6):111-114.
[18]曹小平,程静.基于微信的自助查询系统的设计与实现[J].重庆工商大学学报:自然科学版,2014,31(2):66-69.
[19]林杰,付梦印,邓志红,等.主-从滤波器设计及其在传递对准中的应用[J].控制理论与应用,2011,28(10):1447-1450.
[20]Marthinus C.Havinga.Flight Test Results of a MEMS IMU Based Transfer Alignment Algorithm for Short Range Air-to-Air Missiles[C]//AIAA Guidance,Navigation,and Control (GNC) Conference,Boston,2013:1-10.
(责任编辑 杨继森)
Method of Flexure Compensation Model Based on ARMA in Master/Slave INS Calibration
ZHOU Da-wang1,ZHAO Guo-rong1,WU Guo-sheng2
(1.Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China; 2.The 91697thTroop of PLA, Qingdao 266405, China)
For the ship master / slave INS calibration deflection compensation model, we proposed a modeling method based on ARMA. This method first modeled the flexure based on ARMA. The model identification data sequence outputted from the slave INS differential data. Model identification method used least squares parameter estimation method. Model order identification used the AIC criterion. The model test usedχ2test method. Then, based on this model, we used the “velocity+attitude+angular velocity” matching master/slave INS calibration to design comprehensive compensation filter. Filter was expanded deflection model design to the system state. Finally simulation studies were researched. Simulation results show that the modeling method is effective.
inertial navigation; flexure; online calibration; ARMA
2015-02-14
国家自然科学基金(61473306);装备预研基金项目(9140-A09040112-JB14110)
周大旺(1984—),男,博士研究生,主要从事惯性导航研究。
10.11809/scbgxb2015.08.026
周大旺,赵国荣,伍国胜.主/子惯导标定中挠曲变形的ARMA补偿方法[J].四川兵工学报,2015(8):104-108.
format:ZHOU Da-wang,ZHAO Guo-rong,WU Guo-sheng.Method of Flexure Compensation Model Based on ARMA in Master/Slave INS Calibration[J].Journal of Sichuan Ordnance,2015(8):104-108.
V249
A
1006-0707(2015)08-0104-05

