最小势能原理中总势能表达式的理解

郭空明 徐亚兰

(西安电子科技大学机电工程学院，陕西 西安 710071)

最小势能原理中总势能表达式的理解

郭空明 徐亚兰

(西安电子科技大学机电工程学院，陕西 西安 710071)

介绍了最小势能的原理，就最小势能原理中弹性体总势能表达式的理解难点进行了说明，通过一个简单系统中能量的变化，着重阐述了外力势能的含义，并得出了一些有助于深入理解弹性体总势能的结论。

最小势能原理，总势能，外力势能

1 最小势能原理中弹性体的总势能

最小势能原理又称为最小位能原理，其作为固体力学的重要能量原理，在《结构力学》《弹性力学》等课程中均有讲授，且在土建、航天等结构领域存在广泛的应用。该原理可视为质点与刚体系的拉格朗日—狄利克雷定理在弹性体中的推广，其中的总势能表达式定义为弹性体应变能U与外力势能V之和：

∏=U+V

(1)

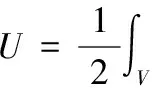
代表弹性体内储存的应变能，该表达式并不存在理解困难。下面讨论外力的势能，为简单起见，假设弹性体只受集中力作用，则外力的势能定义为集中力与其作用点位移乘积的负值：

V=-PTΔ

(2)

根据该定义，一些教材将外力势能阐述为外力做功的负值，但这就与克拉皮隆定理产生了矛盾。在克拉皮隆定理中，规定外力从零开始缓慢加载，因此外力做功为集中力大小与其作用点位移乘积的一半，且全部转化为弹性体的应变能。而且，运用式(1)进行总势能计算时，往往会得到总势能为负值的情况。由于加载前系统的总势能为零，那么如何从能量转换观点对总势能表达式进行理解，是一个难点。由于大部分教材并未对该表达式进行深入说明和分析，许多初学者对此往往感到困惑。学术界也存在广泛的争议，如一些学者认为外力的做功为虚功，而一些学者认为，该表达式中的总势能并不是真实的总势能。

由于弹簧质量系统可以看作最简单的弹性系统，为了说明问题，下文以一个弹簧质量系统为例，分别对于无限缓慢加载和常力加载两种情况，分析系统变形和恢复过程中能量和做功的问题，指出：式(1)中的外力势能确实是外力做功的负值，但此时的外力做功大小并非加载时所做的功，而应是变形恢复时外力所做负功的绝对值，前者在数值上是后者的一半。而最小势能原理中的总势能确实代表了弹性体真实的总势能。

2 无限缓慢加载的弹簧—质量系统

对于真实的弹性体，由于惯性的存在，导致载荷不仅会改变系统的弹性势能，也会改变系统的动能。因此在静力学教材中，都规定载荷必须无限缓慢地从零增加。考虑无阻尼弹簧质量系统，其中弹簧的刚度为k。当系统不受外力作用处于平衡时，令系统受到一个从零缓慢变化至F的外力，这样，系统可以认为是准静态变化的，系统达到最终平衡状态时将不具有动能。由于不考虑阻尼，过程中并没有能量损耗。显然系统达到最终平衡时弹簧的变形量为Δ=F/k，则系统的应变能为：

而外力所做的功为：

由上式可知应变能完全等于外力做功，此时外力在弹性体变形阶段所做的功为力与位移乘积的一半，完全转化为系统的应变能。

而根据最小势能原理的定义，静平衡时系统的总势能为：

(3)

从总势能的数值可以看出，存在两个问题，首先，系统的总能量似乎“不守恒”，加载前，系统的动能与势能之和显然为零；加载后，系统动能仍然为零，而势能变成了负值，动能和势能之和也成为负值。其次，此时的外力势能并不等于外力加载时所做的功，而是其2倍。

要理解这些问题，首先要考虑力学中势能的定义。按照力学的一般说法，任何一个实际状态的弹性系统的总势能，等于这个系统从该实际状态运动到某一参考状态(通常取弹性体无形变的状态作为参考状态)时所有作用力所做的功。

弹性系统的作用力包括外力和内力，内力势能就是应变能U，因为无论加载还是卸载，应力总是和应变同方向的，所以应变能是正值。而且无论加载还是卸载时，应力都与应变成正比，无形变时应力为零，因此应变能表达式前有系数1/2。而外力势能是结构从实际位置恢复到它的初始状态(未变形状态)时，外力所做的功。虽然加载方式考虑了缓慢加载，但变形后外力的大小就不再随变形量发生变化，因此恢复变形时，外力所做的功为外力大小与变形量乘积一半的负值，没有系数1/2。

下面具体针对弹簧质量系统的问题展开讨论。显然，矛盾来源于加载和恢复变形时外力性质的改变。加载时，外力是从零缓慢改变至F，而为了计算系统总势能而考虑系统的恢复变形过程时，外力的大小却始终为F保持不变。所以加载和卸载时外力做功的大小并不相同。实际上，虽然对于加载和恢复变形这两个过程每一个过程而言，系统的外力都是保守力，但是两个过程中的力场是不同的，因此不宜将两者纳入同一体系研究能量的变化。

为了更好地说明问题，下面考虑加载和恢复变形时力场相同的情况。

3 以常力加载的弹簧—质量系统

考虑弹簧—质量系统初始状态弹簧变形量为零，质量块也没有速度的情况下，系统受到一个大小为F的突加载荷。在这种情况下，弹簧在静平衡位置的变形量仍然为Δ=F/k，但是与无限缓慢加载的情况不同，当弹簧达到静平衡位置时外力做功大于系统的应变能，多余的能量转化为系统的动能T。静平衡状态时系统的应变能为：

而外力所做的功为：

多余的能量转化为系统的动能，为：

而此时静平衡状态时系统的总势能仍然为：

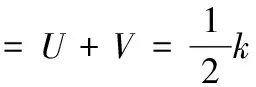
但此时存在动能，因此总能量为：

E=T+∏=0。

由于真实系统存在阻尼，动能会逐渐衰减为零，最终系统将在静平衡状态取得平衡。可以看出，在变形和恢复变形过程中，力场均为恒定力场的情况下，能量的守恒是显而易见的，加载前以及达到静平衡位置后的总能量均为零，而且外力的势能大小既等于加载时外力所做功，也等于卸载时外力所做功。实际上，只要加载和卸载时，力场的特性保持一致，均不会出现理解上的问题。对于无限缓慢加载的情况，若卸载时的外力也随着变形量与加载时保持相同的变化，也不会出现理解的矛盾。

4 结语

大部分静力学教材为了使知识体系完全处在静力学框架中，均认为外力的加载是无限缓慢的，而加载达到平衡状态后，外力大小保持不变。这就造成了加载和恢复变形两个过程中力场不一致的情况，从而导致了理解上的难度。本文通过一个最简单的例子分析了这一点，指出在静力学教材中最小势能原理中弹性体总势能的表达式中，外力势能应理解为恢复变形时外力所做的负功，因此并不是虚功。而总势能也确实代表了弹性体真实的总势能。

[1]BauchauOA,CraigJI.Structuralanalysis:withapplicationstoaerospacestructures[M].Berlin：Springer,2009.

[2] 龙驭球，包世华，袁 驷，等.结构力学教程(下册)[M].北京：高等教育出版社，2000.

[3] 陈位宫.力学变分原理[M].上海：同济大学出版社，1989.

[4] 刘正兴，孙 雁，王国庆.计算固体力学[M].上海：上海交通大学出版社，2000.

[5] 白 冰，李小春，石 露，等.对弹性静力学中外力功表达式及相关问题的探讨[J].力学与实践,2011,33(5)：67-69.

[6] 黄耀英,王润富,李春光.基于能量变化过程分析弹性力学总势能[J].力学与实践,2015,37(2):249-252.

On understanding of total potential energy formula based on principle of minimum potential energy

Guo Kongming Xu Yalan

(SchoolofMechatronicEngineering,XidianUniversity,Xi’an710071,China)

The paper introduces the principle of the minimum potential energy, indicates the difficulties in understanding the elastic total energy formula in the principle of the minimum potential energy, illustrates the concept of the external force potential energy according to the energy changes in the simple system, and concludes the deeper understanding of the elastic total potential energy.

minimum potential energy, total potential energy, external force potential energy

2015-06-27

郭空明(1985- )，男，讲师； 徐亚兰(1971- )，女，副教授

1009-6825(2015)25-0244-02

TU311

A