由两道高考数学真题解析引发的启示与思考

☉江苏省姜堰中学 李彦

由两道高考数学真题解析引发的启示与思考

☉江苏省姜堰中学 李彦

高考是无形的指挥棒，牵动着千千万万个家长、教师、学生的心，高考试题的示范性与导向性影响着高中数学课程教学的发展方向和深度控制，处于一线的高三数学教师与学生一直加强对高考数学真题的分析与思考，笔者在探析各地高考数学试题的过程中，偶然发现两道试题中部分问题的构思、情境创设、具体解析十分相似，由此也引发了不少启发与思考，现呈现给大家共享，旨在抛砖引玉，希望能够引起同仁们的进一步关注与思考，不当之处敬请批评指正.

一、基于两道高真题的回顾与探析

例1（2013年陕西理科卷21题第2问）已知函数f（x）=ex，x∈R，设x＞0，讨论曲线y=f（x）与曲线y=mx2（m＞0）公共点的个数.

解析：根据题意令ex=mx2，即，则曲线y=ex与y= mx2的公共点的个数问题转化为曲线与直线y=m 的交点个数问题；令，则存在u′（2）=0.当x∈（0，2）时，u′（x）＜0，则u（x）在（0，2）上单调递减；当x∈（2，+∞）时，u′（x）＞0，则u（x）在（2，+∞）上单调递增.可见，u（x）在（0，+∞）上的最小值为u（2）时，直线y=m与曲线（x＞0）无交点，即曲线y=f（x）与曲线y=mx2（m＞0）无公共点；当时，直线y=m与曲线存在一个交点，即曲线y= f（x）与曲线y=mx2（m＞0）有一个公共点；当时，在（0，2）内存在m（ex＞1）；在（2，+∞）内存在x2=me2使得，由于em＞m，则u（me2）＞m，根据u（x）在（0，+∞）上的单调性可得：直线y=m与曲线y=存在两个交点，即曲线y=f（x）与曲线y=mx2（m＞ 0）有两个公共点.

本题采用参变分离的思想，通过变形等价转化为曲线与直线的交点问题，上述解析中运用了零点存在定理的思想进行解决，在特殊点的选取上可谓是精妙，但对于大部分学生而言，难以找准这些特殊值，在不等式的证明上，不仅要会运用放缩法，而且还要灵活运用ex＞x这一不等关系结论，能够完整地实现这一详细解析过程的学生少之甚少；在实践中，多数学生都是直接给出m＞时存在两个交点的结论，主要是这些学生忽视了判断x→0+、x→+∞时u（x）的极值，由于目前高考对于极限部分没有规定要求，学生对这方面的知识比较缺乏，即使部分学生已经意识到求u（x）的极值，但是没有能力求解特殊极限值，被迫默认趋向于+∞，而这一想法恰恰和正确结论一致，但并不是所有的情况都是这样的，下面我们来回顾江苏省的一道高考试题，如下：

例2（2013年江苏理科卷20题第2问）设函数f（x）= lnx-ax，g（x）=ex-ax，a为实数，若g（x）在（-1，+∞）上是单调增函数，试求f（x）的零点个数，并证明你的结论.

解析：根据题意得：g′（x）=ex-a≥0在（-1，+∞）上恒成立，则ex≥a在（-1，+∞）上恒成立，则lnx-ax=0（x＞0），即则f（x）的零点个数问题转化为直线y=a与h（x）的交点个数问题，由于，则当0＜x＜e时，h′（x）＞递增；当x＞e时0）递减；当x=e时，h（x）在x＞0上取得最大值为在0＜x＜，根据以上信息可以粗略地作出的函数图像，如图1，根据图像得知：当时，直线y= a与h（x）有1个交点，即f（x）的零点有1个；当时，直线y=a与h（x）有2个交点，即f（x）的零点有2个.

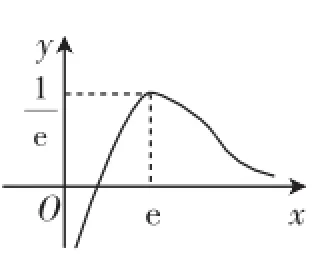
图1

本题处理问题的手段和方法与例1相似，题中确定交点个数的时候利用图像的手段进行处理，在x∈（0，e）上，利用特殊点x=1（即y=0）结合单调性趋势描绘出图像，相对来说比较容易，但是对于x在（e，+∞）上图像的描绘比较麻烦；其实欲想作出比较理想的图像应该求函数h（x）在x→0+、x→+∞上的极限值，学生在例1中通过猜测恰好获取了正确的结论，但是在本题中学生猜测x→+∞时y→0相对比较困难，实践中学生出错的现象较多.

二、从高等数学的角度思考高考试题的解析

上述例1和例2的解析中，我们不难发现当前学生运用现有知识解决问题的局限性，在x→0+的情况下，对于虽然高考没有要求，平时数学教师介绍也少，但是多数学生还是可以解决的，但是对于x→+∞时，两个函数都不是普通的极限问题，学生基本上是不会解决，陷入束手无策的尴尬境地；通过对u（x）和h（x）的极限情形进行分析可知：当x→+∞时，u（x）和h（x）的极限都属于类型的特殊极限问题，极限值存在三种可能性（0、+∞、大于零的常数），从高等数学的角度出发，利用洛必达法则（若函数f（x）和g（x）满足：（1）（2）在点a的某去心邻域内两者都可导，且g′（x）≠0；（3）可为实数，±∞），则）来处理此极限，显得比较简洁、方便.具体如下：这样例1和例2中学生比较麻烦的问题就很快被解决了，而且过程简洁、易懂.

三、高考真题探析中得到的启示与思考

上述两道高考压轴题都涉及同样的问题，命题专家的目的也许是认为采用零点存在定理与函数单调性相结合进行处理是合情合理的方案，这样的试题并没有超纲，在高中所学数学知识与能力的范围内能够处理，但在高考的浪潮中，作为许多那些希望进入名牌大学、重点大学的学生的数学教师而言，并不满足上述的“繁杂”处理方式，势必会在平时的高考数学复习中引入洛必达法则等这些高等数学的结论与定理，无形中会增加学生的学习负担；当然，在高考数学试卷中出现高等数学雏形的案例已经不足为奇，在前几年的高考试题中所出现的“拉格朗日中值定理、凸函数的判断”等都是很好的例证；那么在高中数学课堂教学中是否要去追求这种“高等数学热”？作为命题专家应该如何面对这一“敏感”问题？笔者提出了一些笨拙的见解如下：

全国各省市一直在追求“公平、公正、公开”的高考原则，各项制度越来越完善，每年都会编拟出台各学科的《考试说明》，文中两个案例从理论上讲并没有超纲，符合考试说明的要求，但在解答中，如果有学生利用高等数学的结论进行快速解题获取准确的答案，似乎与高考考查学生能力的要求不相称，存在着提前额外了解一些特殊的定理与结论，显示能力较强的嫌疑，由于当前高考的至高地位和高考考题的示范作用，很有可能会导致在高中数学教学中出现追求高等数学热的现象发生，可能会助长学生“投机取巧”不良习惯的养成，对于通过高考题来考查学生运用所学知识处理实际问题的真正能力方面有失公平，影响高考考题对高中数学教学在“度”上积极的指挥作用.

高考数学的命题应该注重多角度论证，避免擦边球现象的发生，特别避免对于那些运用高中数学知识求解繁杂、困难，但是运用高等数学定理、结论解决比较简单、方便、快捷的试题出现；从辩证唯物主义的角度来看，事情总是一分为二的，并不能说高等数学问题下嫁与高中数学教学都是弊端，但是为了避免可能对以后高考数学复习教学的影响，防止高中数学教学过分追求高等数学热问题的出现，完全可以明确限制不允许运用高等数学中的相关定理或结论；在考查的形式上可以发生变化，不直接涉及高等数学现成的概念或定理问题，应该注重对新概念或定义的理解与运用的考查，这很好地体现了对学生实际运用能力的考查.

总而言之，高考试题一直是社会各界特别是高中教师和学生关注的热点话题，高考试题的探究具有重要的现实意义，直接指引着高中数学教育教学方向的发展，影响高中数学教学重点与难点在“度”上的把握，这应该是我们一线高中数学教师应该关注的重要信息.F