数学概念教学重在区分“轻、重、缓、急”

☉江苏省启东市吕四中学 徐磊

数学概念教学重在区分“轻、重、缓、急”

☉江苏省启东市吕四中学 徐磊

“数学根本上是玩概念，不是玩技巧，技巧不足道也”“概念是数学的细胞”“在概念教学上应该做到不惜时，不惜力”……虽然广大教师对概念教学的重要性已经形成共识，但对“数学概念如何教”却存在着较大的分歧.比如，有教师认为“概念教学关键是创设问题情境，好的情境是成功的一半”，也有教师认为“应该注重概念的形成过程，因为过程比结果更重要”，甚至有教师认为“应该发挥学生学习的主动性，让学生主动构建数学概念”……这些观点看上去都非常“在理”，却让人无所适从.正所谓“教无定法”，对于不同的数学概念，不同层次的学生，所采取的教学策略必然有所差异.因此，我们不必过分纠结于数学概念教学的一些细节问题，关键是不能“眉毛胡子一把抓”，要分清楚“轻、重、缓、急”.

一、“轻”教学套路，适合才是最好

在很多教师眼里，数学概念教学就固化为“几部曲”.最常见的是“三部曲”.第一步：创设情境，引入概念.通过生活情境、问题情境，激发学生的学习兴趣，引发认知冲突，从而为引入新的知识进行铺垫.第二步：主动探究，形成概念.在教师的指导下，师生共同努力，经历观察、分析、猜想、验证等思维过程，提炼出数学概念的定义.第三步：强化训练，巩固概念.通过一些典型的例题，进行概念辨析或概念应用，从而加深学生对概念的印象.当然，“几部曲”教法有其一定的理论依据，操作性也比较强，对概念教学具有一定的参考价值，但切不可拘泥于“几部曲”.

在平时教学中，多“一步”、少“一步”也未尝不可.比如，未必所有的数学概念都需创设情境，有些具体形象、浅显易懂的数学概念就用不着在情境创设上大费周章.笔者曾经听过一堂课，上课主题为“球的表面积与体积”，上课教师为了引出“球”的概念，特意创设了一个问题情境：让学生从各种形状的水果中挑出是球形的水果.其实这个情境的创设就有点多余了，高中生怎么会不清楚“球”是怎样的呢？又比如，很多教师用导学案上课，如果把导向案用在概念课上，那就用不着“几部曲”了，学生课前已经自学了相关的内容，对教材的内容基本熟悉，所以此时应该直奔主题，面对学生进行答疑.由此可见，尽管概念课有其一定的教学套路，但具体操作中要灵活变动，适合学生的才是最好的.

二、“重”自然生成，强扭的瓜不甜

数学概念的生成是一个归纳、概括、抽象的过程.在这一过程中，学生往往要从具体的感性材料和已有的知识经验出发，“以头脑中已有的某些自发性概念的具体性、特殊性成分作依托，从中分化出它的理论内涵，使之能借助经验事实，变得容易理解”，从而在自己的知识框架内构建新的数学概念.我们知道数学是“自然”的，当然数学概念的生成也应该是“自然”的.何为“自然”生成呢？关键是做到以下两点.一是生成过程遵循学生的认知规律和认知水平；二是生成过程能彻底打消学生心中的疑虑.

案例1：离心率定义的由来.

（1）在数学发展史中找理由.

研究天文现象需要计算行星的运行轨道，而这些行星的运行轨道通常就是圆扁程度不一的椭圆，而离心率就是为了描述轨道圆扁程度而引入的一个量.不仅如此，天文学家还发现太阳系的八大行星都是绕着以太阳为焦点的椭圆形轨道运行的，这些轨道偏离太阳的程度也不一样，因此他们就把离心率称为“偏心率”.并且行星和太阳之间的距离是在变化的，其中在近日点处离太阳最近，偏离距离为a-c，在远日点处离太阳最远，偏离距离为a+c.当然不能直接用最近距离和最远距离表示偏心率，因为这两个值不仅和运行轨道的圆扁程度有关，还受轨道大小的影响，人们需要构造一个“稳定”的量来表示偏心率.最后经过反复尝试，发现的值和椭圆大小无关却能很好地刻画椭圆的圆扁程度，因此，大家就选择了表示离心率.

（2）在圆锥曲线的定义中找理由.

这回从椭圆的定义入手开始推理.椭圆是平面内到两定点的距离之和为常数的点的轨迹（其中到两定点的距离之和为2a，两定点的距离为2c，且2a＞2c），定义中涉及的参数是a和c；另外圆锥曲线的统一定义为“到定点的距离与到定直线的距离之比为常数”，而这个常数的值恰好是.由此可见，a、c是描述椭圆定义乃至圆锥曲线定义的基本参数，所以用来表示离心率更加名正言顺.

以上两大理由充分揭示了“离心率”由来的问题，学生“心服口服”，从而保证了“离心率”概念生成过程的自然.但要做到“自然”生成却并非易事，有时需要查阅文献资料，对概念的产生进行合理地推理论证.

三、“缓”实战应用，磨刀不误砍柴

有相当一部分的老师认为“高考基本上都是概念的应用，很少直接考概念的表述”，因此，教师在数学概念的教学过程中过于强调数学概念的知识本位，有意无意地压缩概念形成过程的教学，导致新授课教学变成了“应用”课教学.更有甚者，很多教师在讲解概念时，没有让学生对其必要性获得足够的感性认识，而是直接给出数学概念，导致学生只会死记数学概念，而没有真正理解数学概念的实质.

案例2：几何概型.

教师花10分钟左右，把几何概型的定义向学生讲解完毕.接下去，进入应用环节，一口气给出了5个问题.

问题1：如图1所示，将圆盘分成两个区域，两圆半径之比为1∶2，染上红、白两色，向圆盘投掷飞镖.问：投中红色区域的概率是多少？

问题2：取一根长为3m的绳子，如果拉直后在任意位置剪断，那么剪得的两段的长都不小于1m的概率有多大？

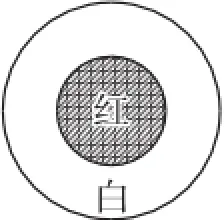
图1

问题3：在500mL的水中有一只草履虫，现从中随机取出2mL水样放到显微镜下观察，求发现草履虫的概率.

问题4：取一个边长为2a的正方形及其内切圆，随机地向正方形内丢一粒豆子，求豆子落入圆内的概率.

问题5：在1L高产小麦种子中混入了一粒带麦锈病的种子，从中随机取出10mL，含有麦锈病种子的概率是多少？

本节课最大的问题是在数学概念的建立和理解上所花的时间太少，只占整个课堂的20%，而将80%的时间花在习题训练上.这种“短、平、快”的战术缩短了学生的认知过程，虽然加快了教学进度，但学生对概念的理解难以深入，对某一个概念学习的经验很难迁移应用到其他数学概念的学习中去，容易导致概念学习连贯性的缺失.其实，只要学生理解几何概型的实质后，几何概型的运算一般是“长度比、面积比、体积比”也就很好理解了，用不着大量的重复训练.

四、“急”建立联系，根深才能叶茂

布鲁纳曾说过：“学生获得的知识如果没有完整的结构把它联系起来，那是一种多半会遗忘的知识.”在数学概念的学习中，并不存在孤立地学习某个概念的情形.概念之间的相互联系决定了学生的学习是建立图式和产生式系统的过程，这种认知结构必须是学习者通过自己对信息的加工去建构的，是学习者自主性和能动性学习的结果.在概念的获得中，学生如果不能从多背景、多角度理解概念，没有在头脑中形成概念域或者概念系，那么一旦换一个方式去阐述同一个概念，即如果给出概念的另一表征形式，就会导致学生不知所云.因此，建立数学概念间的联系是当务之“急”.

案例3：正弦定理与余弦定理.

在教材中（人教A版），正弦定理的推导是先作三角形的高线，然后转化为直角三角形，利用三角形的高相等的条件得到；余弦定理的推导则是利用向量的数量积的定义.两种推导工具，两种推导方法，得到两个定理，表面上看正弦定理和余弦定理风马牛不相及，似乎看不出它们之间存在着任何联系，但实际上是这么回事吗？

结论1：由余弦定理能推出正弦定理.

因为a2=b2+c2-2bccosA①，b2=a2+c2-2accosB②，①-②，化简得a2-b2=c（acosB-bcosA），

结论2：由正弦定理能推出余弦定理.

因为在三角形中A+B+C=π，则sinA=sin（B+C）= sinBcosC+cosBsinC，两边平方得sin2A=sin2Bcos2C+ cos2Bsin2C+2sinBcosCcosBsinC.把余弦的平方用正弦的平方代入得sin2A=sin2B（1-sin2C）+（1-sin2B）sin2C+ 2sinBcosCcosBsinC.化简得sin2A=sin2B+sin2C-2sin2Bsin2C+ 2sinBcosCcosBsinC=sin2B+sin2C-2sinBsinC（sinBsinC-cosBcosC）=sin2B+sin2C-2sinBsinCcosA，即sin2A=sin2B+ sin2C-2sinBsinCcosA①.

同理，也可以推导出余弦定理的另外两个公式.

正弦、余弦定理不仅仅是解三角形和实现三角形边角转化的工具，通过上述推导，学生又会产生一个新的认知，那就是正弦、余弦定理的统一性.于是余弦定理的知识网络也就形成了，从而有利于学生从整体上把握数学概念.

总之，数学概念最有价值，也最重要，但数学概念教学要做好也并非易事，关键是在教学中，教师要分清楚“轻、重、缓、急”.

1.吕增锋.基于“自圆其说”理念下的数学概念教学——由“离心率”概念引发的思考［J］．中学数学（上），2015（1）.

2.彭清峰.高中数学概念教学“四部曲”［J］．中学数学（上），2014（12）.

3.吕增锋.打通正弦、余弦定理的“任督”二脉——基于“再认知”理论的复习课教学［J］．中学数学教学参考（上），2014（9）.A