浅谈函数教学中的分类思想
☉江苏省昆山市第一中学 余莉莉
浅谈函数教学中的分类思想
☉江苏省昆山市第一中学 余莉莉
函数是高中数学的核心和重点,函数板块中孕育着很多数学思想方法,诸如方程思想、数形结合思想、分类讨论思想等.思想方法渗透到函数试题中,使原本并不复杂的函数问题变得复杂起来.我们知道,单一的函数教学除了认知基本初等函数和函数性质之外,其难度并不大,但是随着知识整合度的提升、字母参数的渗透,解决问题的时候必须依赖更多思想方法的渗透才能解决.数学家熊庆来曾说过:“分类的思想是数学的瑰宝,我在解决很多复杂的数学问题时,总是将其分类为一部分、一部分,然后就能轻松地解决了.”
从今天的高中函数教学来看,分类思想频繁出现在函数中.分类思想成为考查重点的原因,笔者认为主要是以下几个因素.(1)带参函数的研究:带参函数问题的解决必然会用到分类讨论思想,参数的变化会导致函数图像不断变化,此时研究函数性质需要依赖变量的不同取值,因此分类思想的运用自然水到渠成;(2)应试的需要:我们知道单一函数或确定的模型研究是无法区分学生解决问题的能力的,要在选拔性考查中区分学生问题解决的能力,必然需要思想方法的渗透,这里分类讨论思想是非常重要的区分,一般较难的函数问题,优秀的学生可以分析得极为细致、中等的学生能分析大概情形、能力不足的学生几乎无法将问题清晰地讨论,这就达到了选拔性考试的要求,因此分类思想必不可少;(3)分类能力是思维培养的必经之路:按照国家长期人才培养的战略方针,我们的教育改革致力于将人才培养的方向和模式做出极大的调整,从原本操作型、熟练型人才向创新型、创造型人才转变,而后者的培养需要新课程理念的支撑、需要更高思维的培养,这都离不开分类讨论思想的贡献.因此,笔者认为在数学教学中对分类思想的教学有着重大的影响作用.
一、分类思想的建立
学生脑海中的分类思想从小学就已经有了雏形,比如:我们可以看到小学生跑步达标时会按照性别分类、下棋时按照水平高低分类,分类思想的初步已经运用于生活实践中.但是对于高一学生而言,函数问题中的分类思想建立尚不明确.函数教学中比较明显的分类思想介入始于函数性质教学,诸如奇偶性、单调性等.在研究各种函数图形时,我们发现总有一些特殊的函数形态,可以利用一些概念界定将某类具备特殊性质的函数归为一类.如何在高一函数教学初始就建立合适的分类思想呢?笔者举一个例子.
案例1:“函数奇偶性”概念教学.
师:同学们,让我们来看几幅图片(投影).(设计意图:提供感官上的刺激,提供两种对称的生活来源)

图1:太极八卦

图3:完美对称的蝴蝶

图4:轴对称函数
师:同学们,在初中我们就认识了两种对称,一种叫中心对称,一种叫轴对称.上面给出的四幅图中,你可以对其进行分类吗?
生:左边的两幅图片属于中心对称图形,右边的两幅图片属于轴对称图形.
师:正确!太极八卦是中国古代的武当的标志,它是典型的中心对称图形,第二幅图是过原点的三次函数的演变过程(以后大家会接触到三次函数),第三幅图是自然界中的蝴蝶,多年适应自然生存的结果使其成为一种完美的轴对称生物,最后一个是商业标记麦当劳,是轴对称图形.这些对称在生活中、学习中无处不在.将它们抽象到数学中,我们可以清晰地分为两类,那么今天的函数世界中,我们也有两种特殊的对称需要研究.
生:一种是轴对称函数,一种是中心对称函数.
师:是的.我们将按照关于y轴轴对称、原点中心对称将函数分为几类.只关于y轴轴对称的函数,我们称之为偶函数,只关于原点中心对称的函数我们称之为奇函数,既关于y轴轴对称又关于原点中心对称的函数称之为既奇又偶函数,两种对称性都不具备的称之为非奇非偶函数.根据这一图形性质,我们将函数分为了以上四大类.接下来介绍奇偶函数的定义.
说明:奇偶函数是分类思想在函数世界中的一次典型渗透,这种渗透还有单调性概念的介绍,指数函数、对数函数不同类型的区分等.在函数教学的初始阶段,这些典型的分类思想渗透是函数研究的基本分类所在.笔者认为,教学时用这些概念解决问题固然重要,但是这些概念中如何产生分类意识、如何理解分类的存在,是函数教学中分类思想建立的基本,值得教学深刻思考.
二、分类切入点找寻
上述谈及的是在函数初步中准确地建立分类的想法,培养初步的分类意识.在实际解决函数问题中,如何正确运用分类讨论思想呢?为何如此分类?分类的切入点在哪里找寻呢?这是笔者认为实际解决函数问题的关键.
1.从概念切入
案例2:解关于x的不等式|2x-1|-|x-2|<0.
分析:(1)当x>2时,原不等式转化为:2x-1-x+2<0,得x<-1(舍).
因此,原不等式的解为-1<x<1.
说明:绝对值问题的解决,其基本手段是依据概念分类,即零点分段.
2.从图形切入
分析:本题原解是采用四大类十六小类的代数分类,标准答案极为烦琐.笔者认为,分类讨论的合理性,正确把握切入点的选择,对顺利解决问题有很大的帮助.将原不等式转化为函数利用图形对a进行讨论即可.
(1)a=0时,如图5所示,可得|x|≥|x-1|-1对任意x∈R成立.
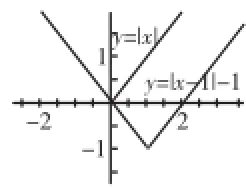
图5
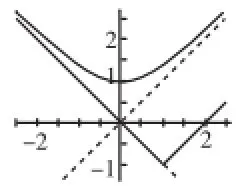
图6
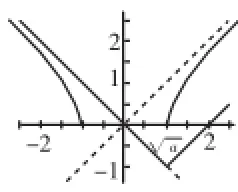
图7

图8
说明:本题的解决手段是利用图形的变化产生分类,相比原解,这种分类较为容易,从直线、双曲线、双曲线焦点的位置确定等入手,解决自然、切入点易发现.
三、分类的更高境界
分类讨论是一种很好的思想方法,它的使用对于我们解决含参变量问题产生了非常有效的作用.但分类讨论思想的更高境界是如何将问题在分类的基础上,研究更高层面的理解,避开分类成为掌握分类讨论思想研究函数问题之后,更高层面的一种感悟.来看一个案例.
案例4:已知函数f(x)=3x2+a,g(x)=2ax+1(a∈R).
(1)若函数f(x)在(0,2)上无零点,研究函数y=|g(x)|在(0,2)上的单调性;
(2)设F(x)=f(x)-g(x),若对任意的x∈[0,1],恒有|F(x)|<1成立,求实数a的取值范围.
分析:本题的第一问比较常规.对于第二问,学生在研究|F(x)|=|3x2-2ax+a-1|在区间[0,1]上的最大值,即研究F(x)=3x2-2ax+a-1在区间[0,1]上的最值时,其思维自然考虑到了二次函数的对称轴对最值的影响,将其分为三种情形进行处理.笔者认为,在学生解决问题的基础上,应该点拨学生反向思考问题,即|F(x)|=|3x2-2ax+a-1|<1要恒成立,则|F(0)|<1且|F(1)|<1,这样将a的取值范围进行了缩小,无须再通过对称轴进行讨论即可解决问题.
解析:(1)由f(x)在(0,2)上无零点,得a≥0或a≤-12.
当a≥0时,y=|g(x)|=2ax+1在(0,2)上单调递增;当a≤-12时,y=|g(x)|=|2ax+1|在上单调递减,在上单调递增.(2)F(x)=3x2-2ax+a-1,x∈[0,1],F(0)=a-1,F(1)= 2-a.
说明:分类讨论思想是解决问题的一种高效思想、优秀思想,函数问题的教学中,分类思想作为一种解决带参问题的基本武器,必须要熟练渗透和掌握.笔者认为在此基础上,给予学生更高的解法指导,指导学生如何在不必要分类讨论的时候简化讨论、避开讨论,对学生合理运用分类讨论思想是一种更好的思维锻炼.如本题中,|F(0)|<1且|F(1)|<1将问题所需研究的变量a的取值范围进行了大幅缩小,使得学生马上理解问题的分类可以简化、避免,这是在充分理解合理分类基础上进行的指导,一题多解的指导有利于培养学生合理分类、避免不必要分类等,提高解决问题的有效性.
总之,分类讨论思想在函数教学中是一种重要的思想方法,其对于解决稍难的函数问题、学生解决问题能力的考查、选拔性测试的区分都有着重要的作用.通过本文,笔者认为分类讨论在函数中的教学需要一步一步实现,笔者将其分为三个不同的螺旋式上升层次,即第一阶段开始培养学生分类讨论的意识和思维,这里的培养往往建立在概念课阶段,不断引导学生针对基础知识清晰地把握分类的存在性和合理性,以及要分类的原因;第二阶段在解决实际问题过程中,运用概念手段进行分类、零点分类、函数性质分类等,以实际解决问题的经验及结合函数基础知识熟练领会分类思想的具体渗透;第三阶段是选择部分一题多解的函数问题,引导学生如何运用分类解决问题以及避免分类解决问题,达到分类思想熟练运用、合理运用的阶段,分是为了不分,这才是分类讨论思想的最高境界.限于篇幅和才疏学浅,笔者对函数中的分类思想还需要继续研究,不足之处请读者指正.
1.沈言.运用分类思想求数列[J].中学数学教学参考(上),2012(10).
2.吴志雄.培养高中生数学应用意识的策略与思考[J].中学数学研究,2010(5).
3.罗增儒.数学解题学引论[M].西安:陕西师范大学出版社,2002.A

