在习题的讲解过程中渗透数学的思想与方法*

☉华中师范大学数学与统计学学院 童扬平 徐章韬

在习题的讲解过程中渗透数学的思想与方法*

☉华中师范大学数学与统计学学院 童扬平 徐章韬

一、引言

要解决“懂而不会”的现象.很多老师可能都有这样的困惑：讲解习题时，讲得非常清楚了，学生却不能理解；或者学生听“懂了”，遇到类似的习题还是不知道该如何动手；学生能听懂老师的讲解，可是自己做题时就是难得“想到点子上”.学生能听懂，却不会想，这表明教师只是教会学生某些具体的招式，却没有教会学生思考.有可能讲解过程只是展示了思维的结果，却没有帮助学生经历思维的过程.在思维过程中，体现了运用数学的思想方法解决问题的方式.如果只是就题论题，没有思维的过程，会出现许多“不自然”的地方，有些步骤就好像从天而降，也因此学生很难真正地从教师讲解习题中有所收获.教师讲解习题时，应该明白解题中蕴含的思想方法，并结合学生已有的认知水平和认知规律，帮助学生经历思维的过程，从而“自然地”弄懂解题过程.只有真正的“懂了”，意识到解题所用到的思想方法，学生才能更加灵活地解决问题［1］.

二、现象描述

某师范院校的六位数学免费师范生，在一所重点高中见习.学校安排每个人在不同的班级讲一节课，内容是“同角三角函数的基本关系”.他们讲解的过程表述十分清楚、明了，学生完全能够“听懂”教师的讲解，可是却不能够灵活应用同角三角函数的基本关系解决问题.本文将对这一次的讲解过程进行具体的分析，探究教师是如何让学生“听懂的”，学生的这种“懂了”是真还是假.

1.同角三角函数基本关系

如图1，P点的坐标是（x，y），MP是正弦线，OM是余弦线，AT是正切线.根据图1，利用勾股定理得到了sin2α+cos2α=1，并且利用比值关系得到了.关于这一部分的讲解过程不是本文的重点，所以在此不再赘述.

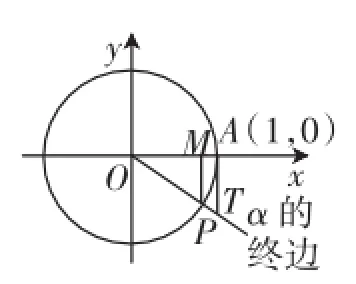
图1

2.讲解例题

问题2：已知tanα=1，求sinα、cosα.这个问题是为了帮助学生巩固对“同角三角函数基本关系”的理解和应用，也是希望学生能够利用方程解题，并且考虑角所在的象限.但是问题出来之后，有学生利用几何方法得到了结果.作出三角函数线得到图2，利用△ATO∽△MPO，得到两个直角三角形的斜边与直角边的比值相等，从而算出一组结果.

学生的解题结果中只包含了第一象限时的情况，而忽略了第三象限时的情况，但是师范生并没有分析学生的解题过程，而是直接就利用第一题的讲题模式开始讲解.仍旧先判断角α所在的象限，然后分情况讨论得到结果.

问题3：已知tanα=m，求sinα、cosα.

此时，正切值不再是一个确定的值，所以角α所在的象限不能够确定.当师范生请学生说解题思路时，大多数学生表现出不自信，不知该如何着手.有学生说，进行分类，分成m＞0和m＜0，然后每一种分类对应着两组解.然后师范生带领学生按照这种思路解题，得到了六组解，最后进行综合成了四组解.

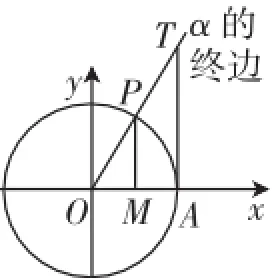
图2

三、分析与讨论

在听课的过程中，师范生讲解完前两个例题，笔者询问周围的学生：“懂了没有”，他们都非常自信的说：“懂了”.但是，当他们看到第三题时，大多数都表现得很不自信，有点儿不敢动手做.其实，读者很容易看到第三个题目与前两个是非常类似的，唯一的区别就是正切值不是确定的，如果学生对前面两题真的懂了就不会表现得如此不自信，因此可以看出学生的这种“懂了”并非真正意义上的“懂了”.接下来，笔者将对三个问题的讲解过程进行详细的分析，探讨出现上述“懂而不会”的问题的真正原因.

对于问题1，从学生给出的答案，可以看出他们已经知道运用同角三角函数的基本关系列方程求解了，而且计算也是正确的.只不过他们在写答案时，没有注意到这代表着四组结果.教师的讲解，一开始就对α进行讨论，首先对角分象限，讨论当角分别在第三和第四象限时，对应的余弦和正切值.学生就会产生疑问：“为什么在开头就要讨论角的象限，明明对任何角都有sin2α+，我一开始就能列出方程.”再遇到类似的题目时，有的学生还是用自己原来的方法，而盲目接受老师观点的学生一开始就会分类，根本不能明白为什么要这么做，这样的教学效果可想而知.实际上，利用同角三角函数的基本关系求解三角函数就是一种方程思想，之所以会分出不同的情况，只是因为解方程时出现了两个根.开始时对角所在的象限进行讨论有如从天而降，并不符合学生的认知逻辑，也不符合方程的思想.

对于问题2，有学生利用数形结合的方法解题可能是老师始料未及的.虽然结果并不完整，但是很明显这位学生在这一题中很好地应用了数形结合的方法，教师不应该不予理会.正确的处理方法应该是先肯定学生的思维，给予他表扬和鼓励.但是老师也需要指出来，如果说正切值变得更加复杂甚至于变成一个代数式子时，这种方法就不再巧妙了.而且用几何方法解题时，可能会出现漏掉一个象限的情况.所以称赞之后，还是要重点讲解利用方程组解题的方法.

对于问题3，这是这一节课的重点和难点，方程的思想也得到了充分的体现.教师对这一题的处理明显也非常的不自然，不管m的正负如何，都有sin2α+cos2α=1，完全没必要先对m进行分类.

问题1和问题2都是教材上的例题，教材编写这两个问题的意图很明显，是希望学生能够利用同角三角函数的基本关系列方程求解三角函数值，分类讨论只是因为角的正负决定了角所在的象限，并不是解决问题的必要步骤.教师的讲解过程没有意识到这一点，只是照本宣科地把教材中的解答过程给学生“讲”了一遍，这样讲解习题学生也能听的懂，但是缺乏真正的启发，学生难以体会解题中所蕴含的真正的思想方法，没有经历将新知识化归为已有的知识的心理过程，所以出现“懂而不会”也就在所难免了.问题3的出现本身可以帮助学生进一步地巩固对同角三角函数基本关系的理解，但是教师的讲解却完全模仿前面的解题步骤，使得这一节课的习题讲解成了典型的“题型+技巧”模式.这种模式就是教师讲学生看，学生再模仿老师的解题过程进行强化训练，缺乏数学学习中本应该经历的直觉、想象、类比、概括等一系列思维过程，使得学生在解题中不顾题目的具体特征而照搬技巧，完全不能体现数学的思维训练价值.

四、总结与思考

解题教学占据了教学的大部分时间，学数学也离不开解题，学生通过解题可以加深对概念的理解，优化数学认知结构，训练数学思维，提高自身分析和解决问题的能力.著名的数学家波利亚曾经说过：“掌握数学就意味着善于解题”；罗增儒说：“数学学习中发生数学的地方都一无例外地充满着数学解题活动”.解题教学的过程就是让学生学习新知、发展智力、提高能力的过程，当然也是帮助学生“学会解题”的过程.解题教学不应该只注重“题型+技巧”，而是要注重思想和方法的渗透，因为思想和方法是对知识融会贯通的理解和升华，而“题型+技巧”只是通过强化训练达到能够熟练地解决旧问题.至于该如何在讲解习题的过程中渗透思想和方法，我们认为需要从以下几个方面入手.

1.精选能够体现思想和方法的习题

要想讲好习题课，首先教师得选择好的习题，也就是能够体现思想和方法的习题，那么何谓能够体现思想和方法的习题呢？数学是自然的、清楚的，数学知识的发展是自然而然的，而数学的思想和方法就是其本质和精要所在，所以能体现思想和方法的好习题应该也是自然的、清楚的，它们应该具备以下特征：首先，与重要的数学基础知识相关，能体现数学概念和性质的关联性；其次，解题的方法是自然、多样的，同时对学生的智力有适度的挑战；再次，表述清晰、明了、流畅.有些偏题、怪题，把知识点进行生硬的叠加，故意制造出大量的障碍，使原本简单的数学概念变得晦涩难懂，不利于提高学生的思维素质和创造性.

2.给予学生思考的权利

根据奥苏泊尔的有意义学习理论，学生有意义的接受学习需要经过一系列积极的思维将新知识融入到已有的知识系统中，也就是说即便是接受学习也需要学生主动地参与思维过程，而不是被动地“被告知”.因此，学生要做到真正的“懂了”而且“会用”，还需要学生自己独立地思考、尝试、探究，要亲自经历概念的概括过程，结论的归纳过程，以及结论推理的演绎过程.教师提出问题之后，要给学生足够的时间让他们自己尝试着去解决，教师要做的是循循善诱，给予心智的启迪，而不是越俎代庖剥夺学生思考的权利，“牵”着学生的鼻子走.

3.提高教师自身的数学教学水平

当教师把某一种题型向学生讲了多次而学生还不会做的时候，教师就应该开始问自己，“是否了解所教内容所蕴含的思想和方法？”“是否懂得学生解决这一问题关键要克服什么？”“自己讲授习题的方式学生能不能懂？”出现“懂而不会”的情况，我们要怀疑的往往是自身的数学教学水平是不是有待提高，而不应该一味地去怀疑学生的数学学习能力.因此，在讲授习题的过程中进行思想和方法的渗透，也需要教师不断地提高自己的数学专业素养和数学教学水平.

1.章建跃.为什么学生听懂了却不会用［J］.中小学数学，2010（12）.

2.熊惠民.数学思想方法通论（第二版）［M］.北京：科学出版社，2012.

3.徐章韬.面向教学的数学知识——基于数学发生的视角［M］.北京：科学出版社，2013.A

*本文系华中师范大学研究生教学研究项目“数学教育方向研究生学术能力提升的研究”（编号：2013JG37）的阶段性研究成果.