男子网球单打技术与综合实力回归预测模型构建分析

蒋启飞 郑 贺

(淮北师范大学 体育学院，安徽 淮北 235000)

1 问题的提出

网球单打综合实力是运动员各种技术运用的综合体现，决定了选手在各种比赛中获胜几率的大小。每年网球ATP-国际巡回赛单打联邦快递指数排名情况是每位参赛选手综合实力的真实反映，是网球单打技术运用的数字化体现。随着网球运动开展的普及，国际赛事不断增加，有关网球比赛中各种技术运用的研究也日益受到人们的关注。如何提高网球比赛中技术运用水平、增大获胜的几率问题，当前学者们从不同的角度进行了研究。比如吴强(2010)通过费德勒与对手技术比较认为:发球成功率、得分率高、ACE 球多是获胜的关键［1］;杨志敏(2010)利用专家问卷法，确定了一发成功率、一发得分率、二发得分率、接发球得分率为比赛获胜的关键制胜因子，并通过这四个因子建立预测比赛胜负判别函数方程［2］;郭立亚等(2010)以选手年终排名积分为因变量，以二发得分率、挽救破发点成功率、接发球胜局率、一发成功率、接一发得分率、一发得分率为自变量进行了回归分析，确定二发得分率、接发球局胜率、挽救破发点成功率为网球单打比赛中的主要制胜因子［3］;周继和(2011)从一发成功率、一发得分率、二发得分率、ACE 球数量、双误个数等技术角度进行网球单打获胜技术的关键分析［4］;何文盛(2011)等对当年世界排名前三的男子单打选手进行了分析，认为一发球得分和一发回球得分能力是制胜的关键因子［5］。从以上的研究文献中不难看出:当前能够代表男子网球单打综合实力的技术因素还没有一个统一的结论。

综合现有的相关研究，主要存在问题如下:第一，回归预测的因变量选择不合理。有的学者把年度最终积分作为选手综合实力排名，忽略了年度积分与运动员参赛次数的关系，而且不同的赛事积分方式也不同，所以不能以年度积分为因变量;第二，部分研究样本选择不具有一般代表性特点。诸如有些学者仅以一场比赛中两个选手的技术进行对比，得出制胜的关键技术因素，因此不具有一般性代表性的特点。基于此，本研究以代表每位选手真正技术实力的因子综合得分为因变量，以联邦快递指数排名前43 位的选手在2014.01.01-2014.10.25 期间所有比赛中技术指标的平均数为自变量，建立综合实力与技术回归预测模型，探求现代男子网球单打比赛中制胜技术的一般性特征，为今后的网球训练与比赛提供有价值的参考。

2 研究对象与方法

2.1 研究对象

该研究以2014.01.01-2014.10.25 期间，参加网球-ATP 世界巡回赛联邦快递指数排名前43 位的男子网球单打选手的技术指标为研究对象。原始技术指标包括ACE 球、双误、一发成功率、一发得分率、二发得分率、挽救破发点、赢得发球局、发球得分率、接一发回球得分率、接二发回球得分率、成功破发率、接发球得分率等;新生变量包括因子得分变量三个、因子综合得分变量一个。

2.2 研究方法

2.2.1 文献资料法

收集整理了网球ATP-世界巡回赛官网［6］(http://cn.atpworldtour.com/)中RICOH ATP(2014.01.01-2014.10.25)男子单打平均每场的技术指标，共计样本43 个作为第一手研究资料，同时在中国知网查阅了有关男子网球单打技术分析的科研文献。

2.2.2 数理统计法

首先，对所收集整理的指标数据在SPSS17.0 软件上进行因子分析，计算每位选手在此期间因子得分;其次，根据所有选手获得的因子综合得分作为因变量进行技术回归预测模型的构建。

3 研究结果与分析

3.1 现代男子网球单打综合实力因子分析

3.1.1 技术指标间的相关性分析

由于本研究的研究方法用到了因子分析，所以检验指标间是否适合因子分析是关键的第一步，否则研究也就失去了意义。在本研究中，网球单打技术指标间的相关性系数检验，采用的是巴特利特球形检验方法(Bartlett Test of Spherictty)与KMO(Kaiser-Meyer-Olkin)检验，检验结果见表1:

表1 KMO and Bartlett＇s Test

上表中，KMO 检验的值为0.639，低于Kaiser 给出0.7 标准，认为样本不大合适做因子分析，但是从巴特利特球形检验结果看，样本的显著性概率P=0.000 ＜0.05，所以认为样本的相关系数矩阵不是个单位阵，因此该样本可以做因子分析。

3.1.2 男子网球单打技术因子结构分析

通过主成分提取法，特征值大于1 的提取原则，共提取三个公共因子，总解释原始变量的方差贡献率为80.484%，符合因子分析中因子变量信息丢失较少的原则。因此，本研究提取三个公共因子是理想的。

表2 男子网球单打比赛技术运用特征因子值与贡献率

从表2 中得知:三个公因子特征值分别为λ1=4.710、λ2=3.483、λ3=1.465，旋转后各自方差贡献率分别为39.251%、29.022%与12.211%，根据因子旋转后的因子载荷矩阵(表3)，此次三个公因子分别命名为“发球局得分效率因子”、“接发球局得分效率因子”、“发球成功率因子”。

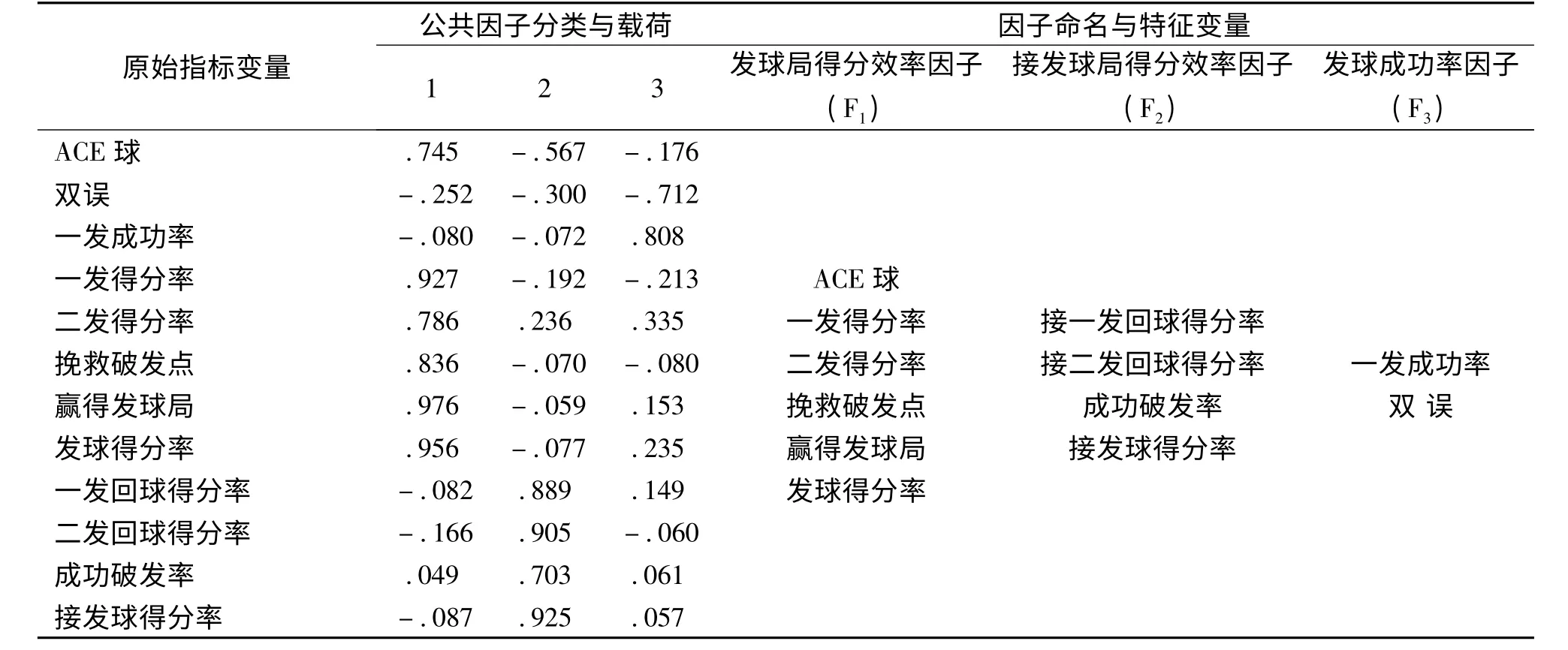
表3 旋转后因子载荷矩阵(Rotated Component Matrix)及命名

3.1.3 男子网球单打技术因子得分模型

依据网球单打技术指标因子得分函数系数(见表4)，三个因子的得分模型公式为

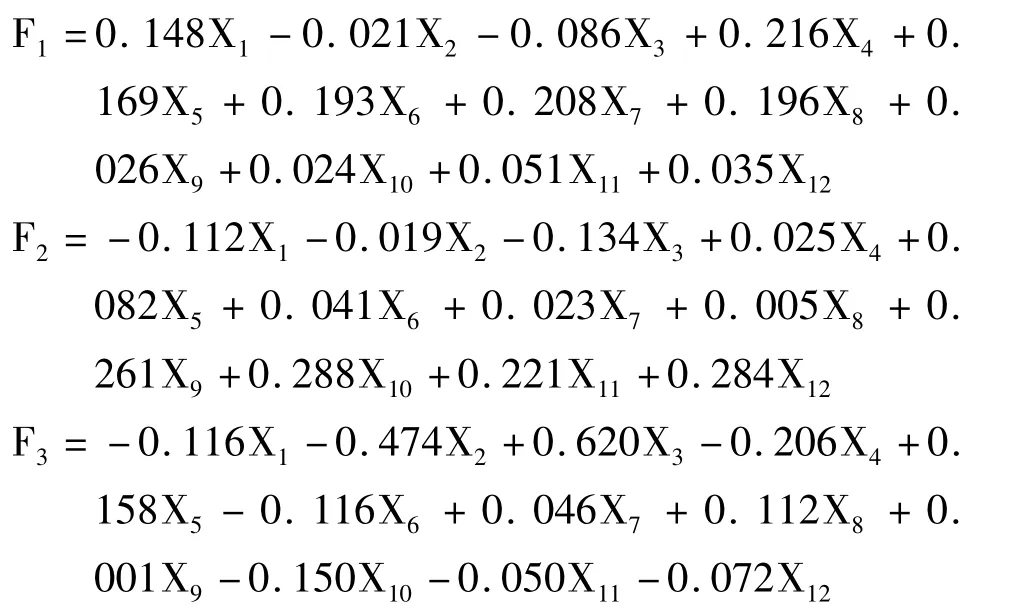
(X1—X12分别代表:ACE 球、双误、一发成功率、一发得分率、二发得分率、挽救破发点、赢得发球局、发球得分率、接一发回球得分率、接二发回球得分率、成功破发率、接发球得分率，以下同。)

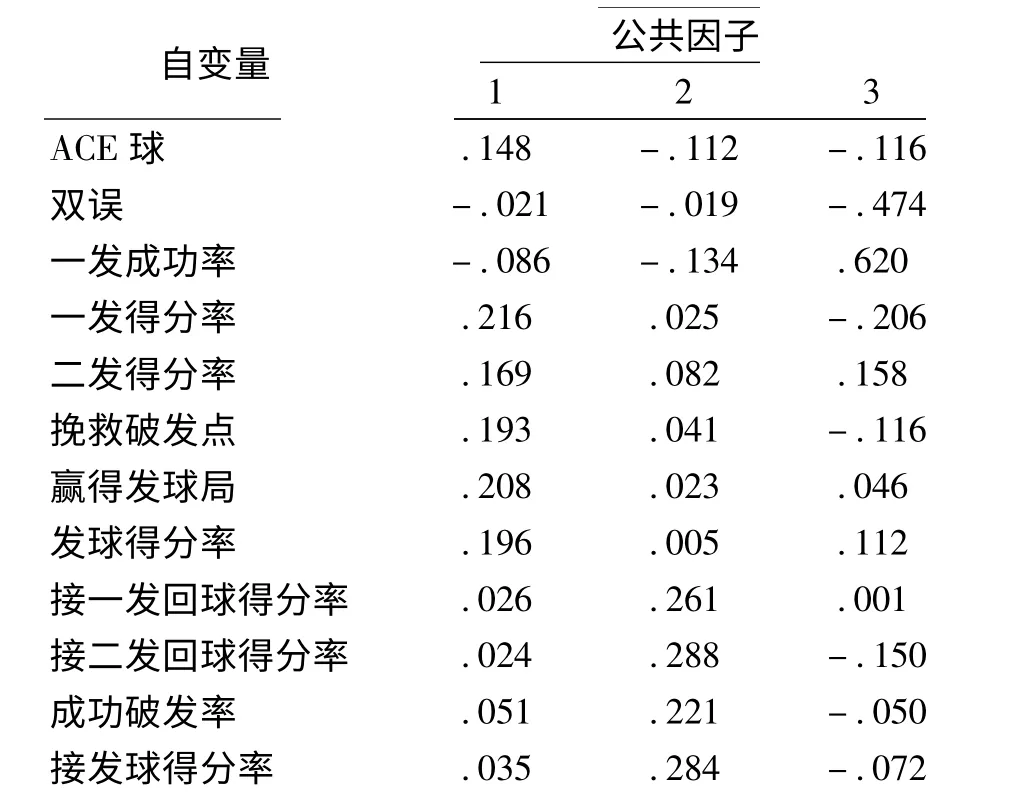
表4 网球单打技术特征因子得分函数系数

由上述分析可知，三个公因子方差贡献率分别为39.251%、29.022%、12.211%，所以网球单打技术因子综合得分模型为:F=39.251F1+29.022F2+12.211F3，通过上述因子得分变量计算，代入单打技术因子综合得分模型，求得每位选手的单打技术因子综合得分，从当前技术运用综合实力看，排名靠前的依次是纳达尔(1.39)、德约科维奇(1.09)、费德勒(1.05)、伯蒂奇(0.70)、穆雷(0.61)、德尔波特罗(0.60)，排名靠后的依次是戈芬(-0.89)、格拉诺勒斯(-0.88)、涅米宁(-0.65)、休伊特(-0.56)、达维登科(-0.56)、蒙菲尔斯(-0.55)，经过对43位选手在此阶段他们胜率与技术综合因子得分的相关性检验，相关系数达到96.342%，属于高度相关，因此可以认为:网球单打技术综合因子得分是衡量选手技术运用综合实力的可靠性参数，相对于其他学者用年度积分作为综合实力考核依据，因子综合得分更具有代表性与客观性。

3.2 现代男子单打技术因子综合得分回归预测模型构建

任何事物的发展都由其内部的主要矛盾与次要矛盾决定。回归分析就是在众多的因素中，寻找具有相对重要性的技术指标作为评价、预测的依据，达到简化评价、预测手段的目的。从本研究看，现代男子网球单打技术指标达到了12 个，如果纯粹用因子分析进行评价、预测，有时候很难发现选手某一技术的优缺点，给有针对性的改进某一个技术环节带来不便，因此用因子分析获得的综合得分变量作为因变量，再次用12 个技术指标作为自变量，进行回归分析，为寻求现代男子网球单打综合实力关键技术突破具有十分重要的意义。

3.2.1 单打技术与因子综合得分相关性分析

回归是为了寻求对因变量起主导性作用的关键性自变量，也是最优回归方程的必然要求。通过对男子网球单打中12 项技术指标与每位运动员的因子综合得分进行简单相关性分析，结果见表5 所示:

表5 单打技术与因子综合得分相关性(双侧)检验

从表5 中看出:在12 个技术指标与因子综合得分相关性检验中，只有ACE 球、一发成功率两项技术指标与综合因子得分不相关，其他十项技术指标都具有显著相关性，相关性从高到低依次为:二发得分率＞赢得发球局胜率＞发球得分率＞挽救破发点＞一发得分率＞双误＞一发回球得分率。因此，二发得分率对技术运用的综合实力影响最大。郭立亚认为:如果运动员要保证二发得分，就必须依赖二发的质量或较高技、战术综合运用水平，当二发质量很高时，发球运动员依然能掌握主动权得分;当二发遭到对方接发球进攻时，运动员也能在被动的情况下通过第三或第四板扭转劣势，所以，二发得分率特别能反映球员的综合技战术水平，是影响比赛胜负的重要指标。

3.2.2 现代男子单打技术因子综合得分最优回归方程的构建

本研究用各选手的技术因子综合得分作为因变量，用上述与因子综合得分具有显著性相关的10 项技术指标为自变量进行了逐步剔除法回归分析，共构建了回归模型12 个，但是根据复相关系数、判定系数、校正判定系数随着模型自变量改变而变化的特点，同时考虑较少的自变量就能获得较高的校正判定系数，选择以“二发得分率、接一发得分率、赢得发球局、接二发回球得分率、成功破发率”做为自变量所建立的回归方程模型符合上述条件，见表6。

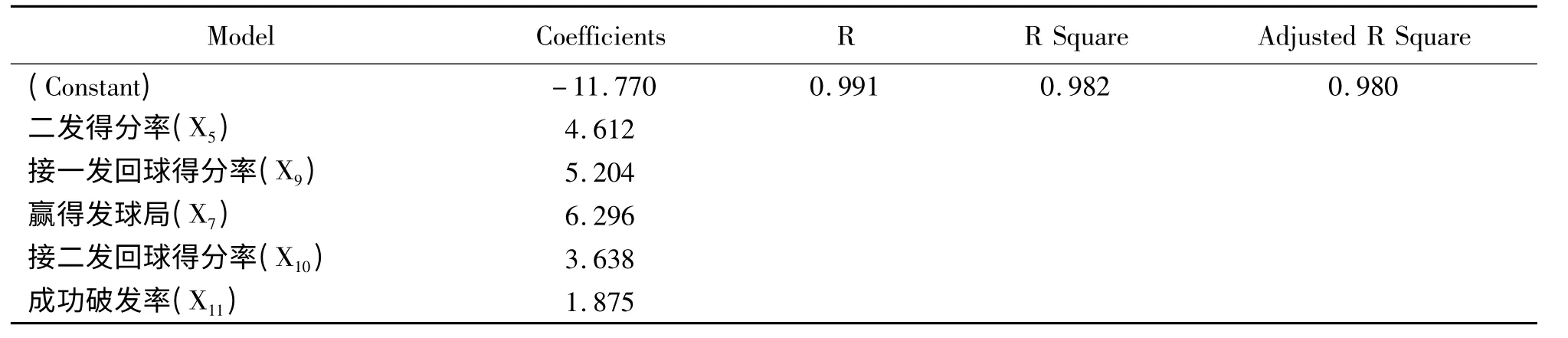
表6 回归方程模型与回归系数综述

从表6 看出，该回归模型方程复相关系数为0.991，判定系数为0.982，校正判定系数达到了0.980，说明拟合优度非常高，具有极高的代表性。根据回归系数，建立的预测回归方程为:^y=4.612X5+5.204X9+6.296X7+3.638X10+1.875X11-11.770，从回归系数绝对值看，很明显对男子网球单打技术综合因子得分影响重要性程度技术指标依次为:赢得发球局百分比、接一发回球得分率、二发得分率、接二发回球得分率、成功破发率。因此，从回归角度看，可以认为:这5 项技术在现代男子单打综合实力预测与评价中属于代表性指标。

3.2.3 回归方程模型的评价与检验

从建立的回归模型方程^y=4.612X5+5.204X9+6.296X7+3.638X10+1.875X11-11.770 看，该方程在评价的实际应用中仅涉及到原始12 项指标中的5 项，大大简化了评价与预测中多指标的处理过程。现在对本次样本实际综合因子得分前20 位选手的单打原始技术指标代入本次构建的回归模型方程中，通过计算得到的预测综合因子得分与实际综合因子得分进行了排位对比，结果如下表:

表7 回归预测模型方程检验结果与实际因子得分比较

从预测模型方程检验结果看出，在实际因子得分前20 位选手中，预测得分非常接近实际综合因子得分，比如纳达尔=1.30，F=1.39;德约科维奇=1.13，F=1.09;费德勒=1.07，F=1.05…等。通过对每位选手预测值与实际得分分值的卡方检验，卡方值都是0.000，显著性概率p=1.000 ＞0.05，因此可以认为本次所建立的回归模型方程预测分值是可信的;同时，从每位选手的实际综合因子得分排位与预测得分排位对比分析，仅有综合实力排在第十三位阿尔玛格洛与第十七位的西里奇改变了原有的位置，在预测得分排名中分别提升一位和两位，而其他18 位选手预测实力得分排位与实际综合实力得分没有变化，准确率达到了90%，说明该回归模型方程的可靠性与可行性。

4 结论与建议

1)因子综合得分是判定男子网球单打技术综合实力可靠性依据。现代男子网球单打技术特征因子是由“发球得分效率因子”、“接发球得分效率因子”、“发球成功率因子”构成的，综合因子得分模型公式为:F=39.251F1+29.022F2+12.211F3，通过此模型能够判断现代男子网球单打选手技术实力水平。

2)建立因子综合得分回归预测方程模型简化了评价过程。通过因子综合得分与男子网球单打具有显著性相关的技术指标，进行二次建立因子综合得分回归预测模型，简化了实际操作中的运算过程，在14 种回归预测模型中，根据最优回归方程的要求，公式为=4.612X5+5.204X9+6.296X7+3.638X10+1.875X11-11.770，该模型方程复相关系数、校正判定系数分别达到了0.991、0.980，说明模型方程具有非常高的拟合优度。

3)因子综合得分回归预测模型方程具有较高的准确性。通过本研究所建立的回归预测模型方程，计算出20 位选手的预测因子综合得分与实际因子综合得分进行了对比，准确率高达90%，所构建的回归预测模型方程具有较高的准确性、可信性，因此用此模型对男子网球单打选手进行综合实力预测也是可行的。

4)建议加强网球单打关键性技术环节改进，有利于提升未来单打比赛中获胜的几率。从本研究所构建的回归模型中:赢得发球局百分比、接一发回球得分率、二发得分率、接二发回球得分率和成功破发率五项技术指标，在综合因子得分评价与预测中处于关键性地位，因此，建议在平时的训练中，进行一些关键性技术环节的模拟训练，以此提高实战中的实效性，比如经常模拟决胜负最后一球的训练、接发球质量较高运动员的接球练习等，从技术模拟与心理压力模拟两个方面进行训练，提高网球单打中的关键性技术水准，使技术运用综合实力得以提升。

［1］吴强.2009 年美网费德勒与对手网球技术比较［J］.体育文化导刊，2010(12):40-42.

［2］杨志敏.男子网球单打比赛成绩预测方程建立［J］.北京体育大学学报，2010，33(4):143-145.

［3］郭立亚，袁毅，关晓燕等.世界顶级网球男子单打比赛制胜技术因素分析［J］.北京体育大学学报，2010，33(2):122-124.

［4］周继和，李 溪，程 亮等.国内外优秀网球单打运动员的技战术特点分析［J］.成都电子机械高等专科学校学报，2011，14(2):37-42.

［5］何文盛，张力为，张连成.世界前3 名男子网球运动员比赛制胜因素技术分析［J］.武汉体育学院学报，2011，45(9):67-73.

［6］2014 年网球ATP-国际巡回赛官网［EB/OL］:http://cn.atpworldtour.com.