利用贵阳单站对流参数的强降水潜势预报方法研究

易志学，兰世怀

(1.贵州省雷山县气象局， 贵州 雷山 557100；2.南京信息工程大学， 江苏 南京 210044)

利用贵阳单站对流参数的强降水潜势预报方法研究

易志学1，兰世怀2

(1.贵州省雷山县气象局， 贵州 雷山 557100；2.南京信息工程大学， 江苏 南京 210044)

该文利用2002—2011年10 a的常规观测资料，筛选出贵阳单站24 h强降水、12 h强降水及6 h强降水个例。对大气温湿类、层结稳定度、热力及能量类物理指标与强降水进行相关性统计分析，确立了相关性较好的常用物理指标(IQ、K、mK、SWEAT、Tg)。通过分析降水前后其物理指标的变化特征，并利用成功指数建立指标预警阈值。再利用逐步消空法和BP神经网络集成方法对指标进行集成，得到相应的预报模型，从而建立了贵阳强对流天气未来0～6 h，0～12 h的潜势预报的预警预报指标，对贵阳地区降雨预报具有一定的指示作用。分析表明，利用逐步消空法建立的预报模型要优于BP神经网络集成的模型。

强降水；对流参数；预警阈值；逐步消空法；BP神经网络；预报集成

1 引言

本文将利用贵阳站地面及高空常规观测资料，分析各种对流参数及物理指标与降水的相关性，寻找出相关性比较好的物理指标，建立贵阳对流天气的预警指标，从而指导人工增雨作业。现阶段我国强对流天气业务专业化处于起步阶段，无论预报时效、预报准确率和技术支撑等与发达国家相比仍存在很大的差距，其中在技术研发方面，利用历史资料提取敏感动力热力因子，经过统计分析，总结出这些指数在各类强对流天气中的分布区间，并确定强对流天气类型的阈值，从而构建具有明确意义并反映强对流特征的冰雹指数、大风指数和超级综合指数等对于目前我国的预报来说仍是一项巨大的挑战[1]。

谌志刚等根据2007—2008年2 a 7—10月广东后汛期强对流天气出现时的雷达资料和对应的GRAPES模式资料以及强对流天气发生时各地的实况，进行数据处理，通过多元逐步回归方法建立后汛期强对流天气潜势预报方程，对广东省后汛期的强对流天气进行0～1 h的临近预报[2]。刘玉玲结合了强对流天气发生发展的物理机制，结合具体个例分析了浮力能和风切变等有关的对流参数在强对流天气潜势预报中的作用[3]。陈秋萍等利用2003—2007年中尺度模式MM5以及探空资料计算的物理量，选取对流天气相关性好的热力、动力、能量参数作为预报因子，通过对这些参数的空间分布特征与强对流天气落区进行诊断统计分析，通过参数搭配，建立了强对流诊断预报方程，制作出了福建省0～12 h，0～6 h强对流天气的潜势预报和落区的预报[4]。许爱华等采用19 a 3—9月常规观测资料，对南昌Δ T 850-500 ≥27 ℃这种强垂直温度梯度与江西强对流天气过程的关系进行了相关分析，并将区域强对流天气、局部强对流天气、无强对流天气3类情况下的中低层气压、温度、湿度、风场及稳定度进行分类合成分析，得出：当南昌Δ T 850-500 ≥27 ℃时，且有天气系统作为触发条件时，江西强对流天气发生的概率达85 %；中低层的低槽和切变等影响系统、江南华南暖湿气流、河套地区的冷空气都有利于江西强对流天气出现[5]。他们的研究主要针对某个区域，且对于强对流天气发生时的物理指标和对流参数的分析中运用的方法是诊断统计分析、逐步回归等方法建立强对流天气的潜势预报模型，而本文的研究主要是针对单站的强降水的对流参数，运用成功指数建立强降水发生的阈值，并逐步消空的方法和BP神经网络集成的方法将相关性好的参数就行集成。

2 资料

2.1 资料概况

本文所用的资料是2002—2011年10 a的常规观测资料，取自南京信息工程学院大气科学学院，是基于MICAPS的分析处理资料。

2.2 强对流天气个例的标准

基于贵阳地区强降水概况，分别定义了不同时段的强降水标准来筛选强降水个例。其中24 h降水量分析中，定义08时的24 h累计降水量大于20 mm的个例为强降水；12 h降水量分析中，定义12 h累计降水量大于15 mm的个例为强降水；6 h降水分析中，定义6 h累计降水量大于10 mm的个例为强降水。根据定义的标准从10 a的常规观测资料中筛选出不同时段的强降水个例来进行探讨分析。

2.3 个例及预报指标选取

从10 a的常规观测资料中，按照2.2的标准筛选出贵阳单站的强降水个例。其中，24 h降水量的强降水共有24个，12 h降水量的强降水共有41个，由于对流参数缺失的原因，实际挑选出36个。6 h降水量的强降水个例总共有54个，由于对流参数缺失的原因，实际筛选出45个。

选取了强降水发生前、发生时的大气温湿类、层结稳定度、热力及能量类物理指标作为分析对象。

3 主要研究方法及常用参数意义

3.1 相关性分析

相关系数是衡量两个变量线性关系密切程度的量，而相关性分析是验证两个变量之间的线性关系，从相关系数r的大小可以判别出，两个变量之间的线性关系的强弱。本文中的相关性分析主要是分析降水发生前，发生时的大气温湿类、层结稳定度、热力及能量类物理指标与降水的相关性，从而确立降水发生时具有较好指示意义的物理指标。

3.2 成功指数

根据表1，有：

(1)

(2)

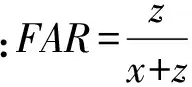
(3)

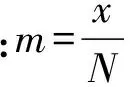
(4)

其中POD的含义为报对次数与事件出现总次数的比值。上面引入的量是衡量预报质量、预报指标或预报方法优劣很有用的参数。寻找预报指标，就是寻找使y和z变小、准确率和CSI变大的条件[8]。本文利用这种方法来确立物理指标的阈值。

表1 定义CSI、POD、FAR、m用表

3.3 逐步消空法

逐步消空法[8]是在3.2中的表达式的基础上，使得y=0，z逐渐变小的方法，可以用探测概率POD与虚假报警率FAR表示：

POD=100.0%

(5)

100.0%>FAR=m>0

(6)

[(FAR)j-1-(FAR)j]>mj%>0

(7)

式(7)中(FAR)j表示第j个指标的虚假报警率。其中，式(6)与式(7)表示“宁空”，式(5)表示“勿漏”；式(5-7)共同表示“宁空勿漏”；而式(5)与式(6)则是“逐步消空法”的数学表达。本文利用这种方法确立的物理指标组合成一个指标集，建立预报思路。

3.4 BP神经网络

BP(Back Propagation)网络[9]，是一种按误差逆传播算法训练的多层前馈网络，它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)3个层次。以建立的物理指标参数序列作为BP神经网络集成预报模型的学习矩阵输入，相应的实况降水量作为学习矩阵的期望输出。首先对学习矩阵的样本进行标准化处理：

(8)

pn为标准化后输入的数据，p为原始数据，max(p)、min(p)分别为P序列中的最大值和最小值。隐节点取5，学习率为0.1，训练函数为tranrp —— 带反弹的回传(Rprop)。对样本进行训练后对给定的实验样本进行仿真。

3.5 指标的种类及物理意义

3.5.1 指标的种类 对流分为干对流和湿对流[10]，本文主要讨论的是湿对流的情况。需满足对流性天气形成的3个基本条件[11]：水汽条件不稳定(包括对流性不稳定)层结、抬升条件。

这3个因子中，水汽和不稳定层结可以看作是对流性天气发生的内因，而抬升作用则看作是外因，当外因和内因相互作用，即当这3个条件都具备时对流性天气将爆发。基于对流性天气发生的3个基本条件，对流天气发生的指标可以分为大气温湿类、层结稳定度、热力及能量类3类。

3.5.2 指标的物理意义 IQ整层比湿积分，反映的是大气层中总的水汽情况。Tg对流温度，气块自对流凝结高度干绝热下降到地面时所具有的温度。如当日最高温度大于对流温度， 则该日就有可能出现热力对流云。热力对流凝结高度一般即为热力性对流云云底的高度。由此可见， 对流凝结高度和对流温度对局地热对流有一定的预报能力。K指数K= (T850-T500) +Td850-(T700-Td700)(9)，反映大气的层结稳定情况，K指数越大，层结越不稳定，但它不能明显表示出整个大气的层结不稳定度。mK指数是考虑了地面温度状况后改进的K指数，其值越大表示气团低层越暖湿，稳定度越小，有利于对流发生。SWEAT强天气威胁指数，I=12Td+20(T-49)+4fs+2f5+125(S+0.2)(10)，是根据日常预报经验得出的一个预报指标，其反应的是不稳定能量与风速垂直切变以及风向垂直切变对风暴的综合作用，当SWEAT强天气威胁指数值越高，发生强对流的可能性就越大。

4 预警指标的筛选

4.1 24 h降水量与预报指标的相关性分析

利用08时24 h降水个例序列，选取对应降水前12 h、24 h的大气温湿类、层结稳定度、热力及能量类物理指标，建立对应的序列，计算出各类物理指标与降水时的相关系数。各类物理指标与24 h累计降水量的相关系数如表2所示。

表2 24 h降水量的相关系数

根据表2可以看出，各类物理指标与24 h降水量的相关系数都较小。其中大气温湿类参数中Tg对流温度与24 h降水的降水前24 h的相关系数比前12 h的要大，而IQ整层比湿积分和TT总指数与24 h降水的降水前12 h的相关系数比前24 h的要好。在层结稳定度类指标中K指数、修正的K指数(mK)、ICC对流不稳定指数、JI指数与24 h降水量的相关性较好，24 h降水量K指数与修正的K指数的前12 h相关性比前24 h的要好，而ICC指数与JI指数的刚好相反。在热力与动力综合类物理指标中SSI指数与24 h降水量的相关系数前12 h达到-0.46，前24 h达到-0.87，可以看做是负相关。与SWEAT的相关系数，前12 h的明显比前24 h大。能量类参数，CAPE与24 h降水量的相关系数，前12 h的高于前24 h的。

根据以上分析，选取Tg对流温度、IQ整层比湿积分、TT总指数、K指数、mK、 ICC、 JI、 SSI、 SWEAT、CAPE作为未来24 h强降水的预报因子。

4.2 12 h降水量与指标的相关性分析

利用08时和20时的12 h水时段降水前、降水时的大气温湿类、层结稳定度、热力及能量类物理指标，建立对应的序列，计算出各类指标物理量与12 h水的相关系数，计算出的相关系数较好的物理参数如表3所示。

表3 12 h降水量的相关系数

根据表3中可看出大气温湿类参数Tg对流温度，IQ整层比湿积分，TT总指数与降水前08时的相关系数比20时要好。在层结稳定度类参数中JI与Teffer的相关系数与24 h的相比较，相关性较小，不稳定，而K指数与mK指数相关性较好。热力动力综合性类参数中SWEAT强天气威胁指数相关性较好。能量类指数CAPE相关性与24小时降水量相比较，相关性很小。

根据以上分析，选区相关性较好的物理参数Tg对流参数、IQ整层比湿积分、K指数、mK指数、JI指数、SWEAT强天气威胁指数、CAPE作为未来12 h降水的物理指标。

4.3 6 h水量与指标的相关性分析

利用6 h降水个例序列，选取降水时段最近的两个时次和降水后的大气温湿类、层结稳定度、热力及能量类物理指标，建立对的序列，计算出各类物理指标与6 h计降水量的相关系数，如表4所示。

表4 6 h降水量的相关系数

根据表4中可以看出大气温湿类参数中降水前与TT总指数的相关系数较好而降水时和降水后的相关系数偏小，Tg对流温度降水前和降水后较好，降水时偏小，IQ整层比湿积分的相关性在降水时达到最大，随后随着大气层中水汽的减小而减小。层结稳定度类参数K指数、mK指数的在降水前、降水时相关性较好，降水后层结稳定度趋于稳定，相关性偏小，ICC指数在降水时相关性较好。热力动力综合类参数中SWEAT强天气威胁指数在降水时相关性最好，相关系数达到0.31。能量类指标在降水前和降水时相关性较好，降水后很小。

根据6 h水相关性分析，选取Tg对流温度、IQ整层比湿积分、TT总指数、K指数、mK指数、ICC、JI、SWEAT强天气威胁指数，作为0～6 h水的预报因子。

4.4 预警指标的确定

通过以上对24 h水量和12 h水量分析以及6 h水量与各类物理指标相关性的分析，不同时段的降水量与各类物理指标的相关系数都较小，无法通过显著性检验，不再进行显著性检验。根据不同时段选取的预报因子可以看出，Tg对流参数、TT总指数、IQ整层比湿积分、K、mK、ICC、JI、SWEAT强天气威胁指数、CAPE等与降水的相关性较好，但是一些参数的相关性不稳定，如TT总指数、CAPE等，最终选取Tg对流温度、IQ整层比湿积分、K指数、mK、SWEAT强天气威胁指数5个因子作为预报指标。

5 预警指标值的建立

5.1 预警指标的分析及确定

根据成功指数的思想分别确立了08时和20时的所选出来的各个对流参数的阈值。

6 h降水预报因子08时阈值的确定，IQ整层比湿积分707.1为临界值，在所选18个个例中，17个个例的值均大于所选临界值。K指数选取12为临界值，在所选18个个例中，16个个例的值均大于所选临界值。SWEAT选取54.4为临界值，所选18个个例中，16个个例的值均大于所选临界值。Tg选取254.1为临界值，所选18个个例的值均大于所选临界值。类似的选出6 h降水20时，12 h降水08时、20时，24 h降水前12 h预警指标的阈值如表5、表6、表7所示。根据以上分析得出，可以看出无论是24 h降水、12 h降水还是6 h降水前的预警指标的阈值相差不大，综合分析，最终确定预报因子的阈值，如表8所示。

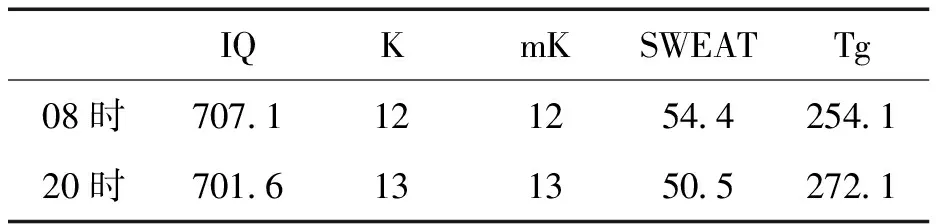
表5 6 h降水量预报的阈值

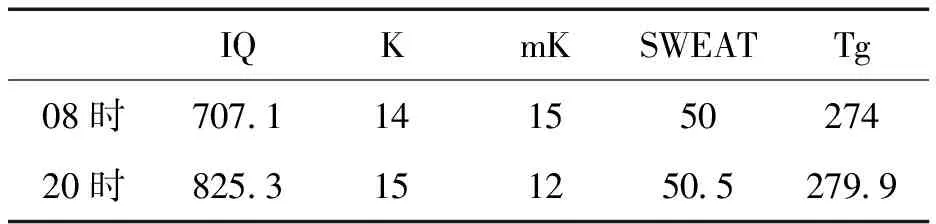
表6 12 h降水量预报的阈值

表7 24 h降水量预报的阈值

表8 最终选取的因子的阈值

5.2 基于逐步消空法预报因子建立

建立强降水潜势预报模型的几点说明：①贵阳属于季风湿润型气候，降水量较多，强度大。②贵阳的探空资料每日只有08时和20时两个时次的观测，资料的时间分辨率不高，而强降水具有时效短、强度大等特点。③在24 h强降水与预报指标的相关性分析中，相关性较小。

在考虑以上几点的基础上，制作预报模型时只考虑0～6 h，0～12 h的预报时效，不考虑24 h的强降水预报。

基于表8建立预警指标的阈值，运用逐步消空的思想建立0～6 h，0～12 h强降水预警指标集合。

①利用IQ整层比湿积分消空，IQ整层比湿积分，数值越大表示大气层中的水汽条件。2011年4月的30 d里，利用08时和20时的探空资料进行消空，满足IQ>707的时次有30次，12 h强降水出现2次，强降水发生的概率为2/30=6%；6 h强降水出现1次，强降水发生的概率为1/30=3%。选择IQ>707作为未来12 h的第1预警指标，记作X1。

②利用K指数消空。2011年4月1-30日，根据08时和20时的探空资料得到K指数，选择K>13作为未来12 h的第2预警指标，记作X2。同时满足X1和X2的强降水次数有14次，12 h强降水发生率为2/14=14%，6 h强降水发生率为1/14=7%。增加X2后12 h强降水发生率增加了约8%，6 h强降水增加了4%。

③利用mK指数消空，选择K>15作为未来12 h的第3个预警指标，记作X3。同时满足X1、X2、X3的强降水次数有13次，强降水发生率为2/13=15%。增加X3后强降水发生率增加了约1%。

④利用SWEAT强天气威胁指数消空，其数值越大表示发生强对流天气的概率越大。选择SWEAT>33作为未来12 h的第4预警指标，记作X4。在2011年4月1-30日中，同时满足X1、X2、X3、X4 4个条件的次数有13次，12 h强降水发生率为2/13=15%，6 h强降水发生率为1/13=7.6%。

⑤利用Tg对流温度进行消空，选择Tg>254.1作为未来12 h的第5个预警指标，记作X5。在2011年4月1-30日中，同时满足X1、X2、X3、X4、X5 5个条件的次数有13次，强降水发生率为2/13=15%，6 h强降水发生率为1/13=7.6%。

由上述讨论得出X1、X2、X3、X4、X5为贵阳地区未来0～6 h，0～12 h强降水预警指标集。

预报流程：将逐步消空法得出的指标集记作Xb，首先利用当日MICAPS资料分析当日的环流形势是否对降水有利，如果有利，则满足用下一个指标IQ整层比湿积分进行判别；不满足则未来6 h、12 h内无强降水发生，满足则进行下一个指标K指数的判别；同样如果不满足则判别为未来6 h、12 h内无强降水发生，满足则继续进行下一个物理指标的判别。以此类推，直到预报指标集里面每个物理指标都能满足条件，才能预报未来6 h、12 h内有强降水发生，如图1所示。

图1 逐步消空的预报模型

5.3 基于BP神经网络预警指标的建立

应用BP神经网络方法，对以上所选对流参数(IQ、K、mK、SWEAT、Tg)建立预报模型，经过调试，当隐节点数取5，学习率为0.1时，得到的预测网络预报模型较好，网络的初始权值是随机设置的通过训练优化，争取达到最小的误差。其中在拟合的过程中只要拟合或者试报的结果大于10 mm和15 mm，可以看作是未来0～6 h、0～12 h内有强降水发生。根据5.2的预报模型的几点说明，只对0～6 h，0～12 h的预报时效进行预报集成，不做24 h的集成预报。

对6 h降水量的参数集成，拟合的均方误差为7.23，拟合结果如表9所示，拟合图为图2所示。同时对12 h降水量的参数集成，拟合的均方误差为25.59。拟合结果如表10所示，拟合图如图3所示。

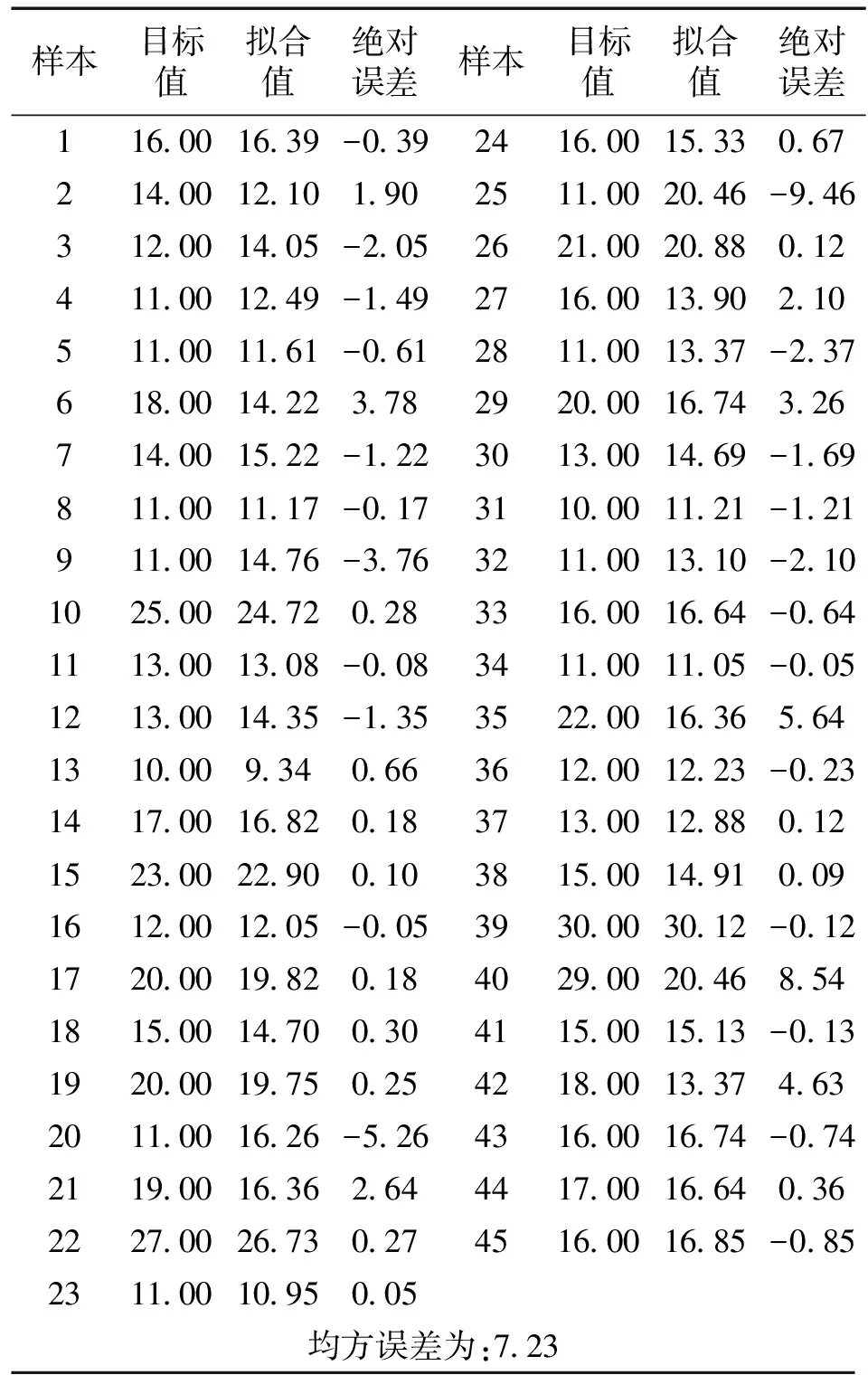
表9 6 h降水量拟合结果

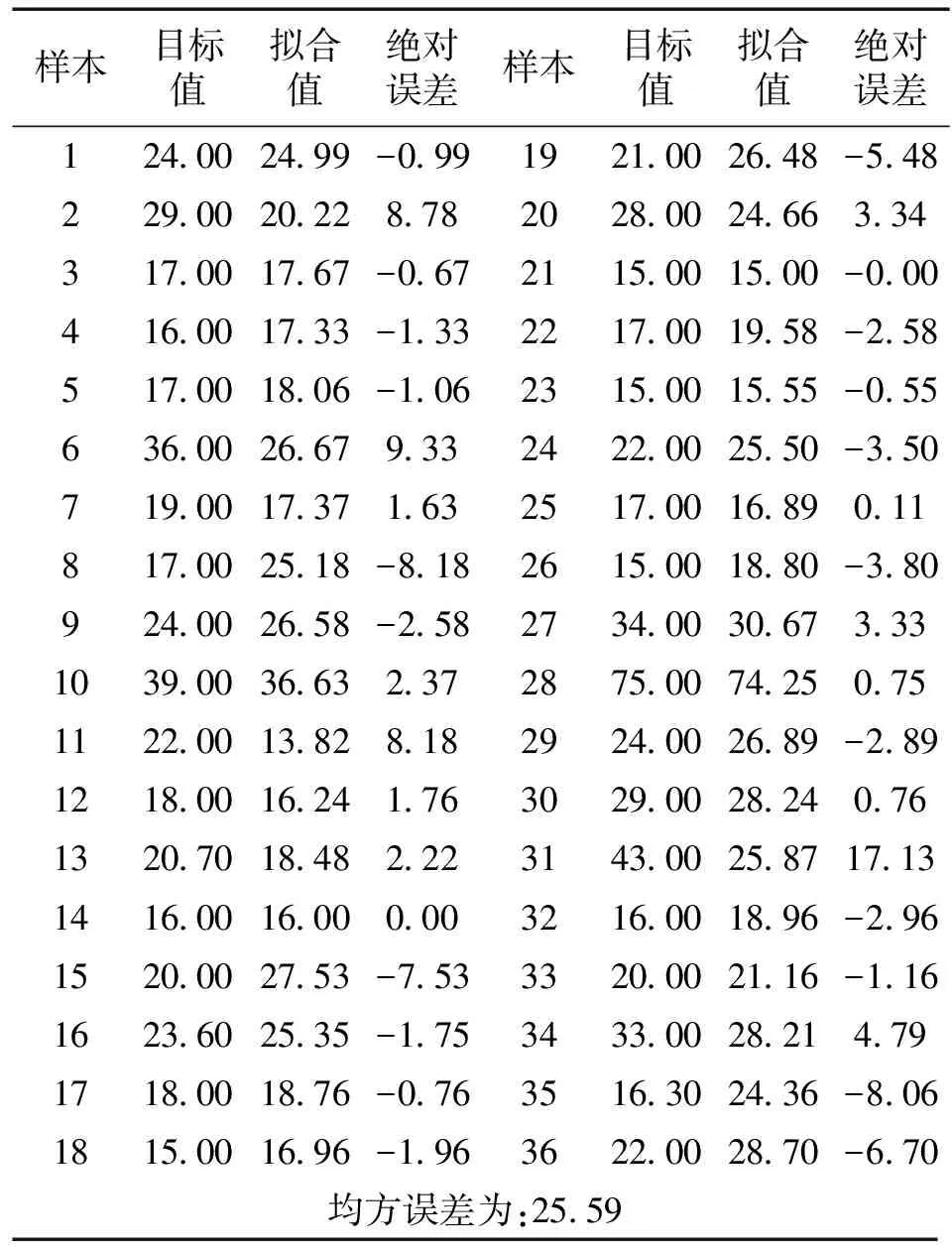
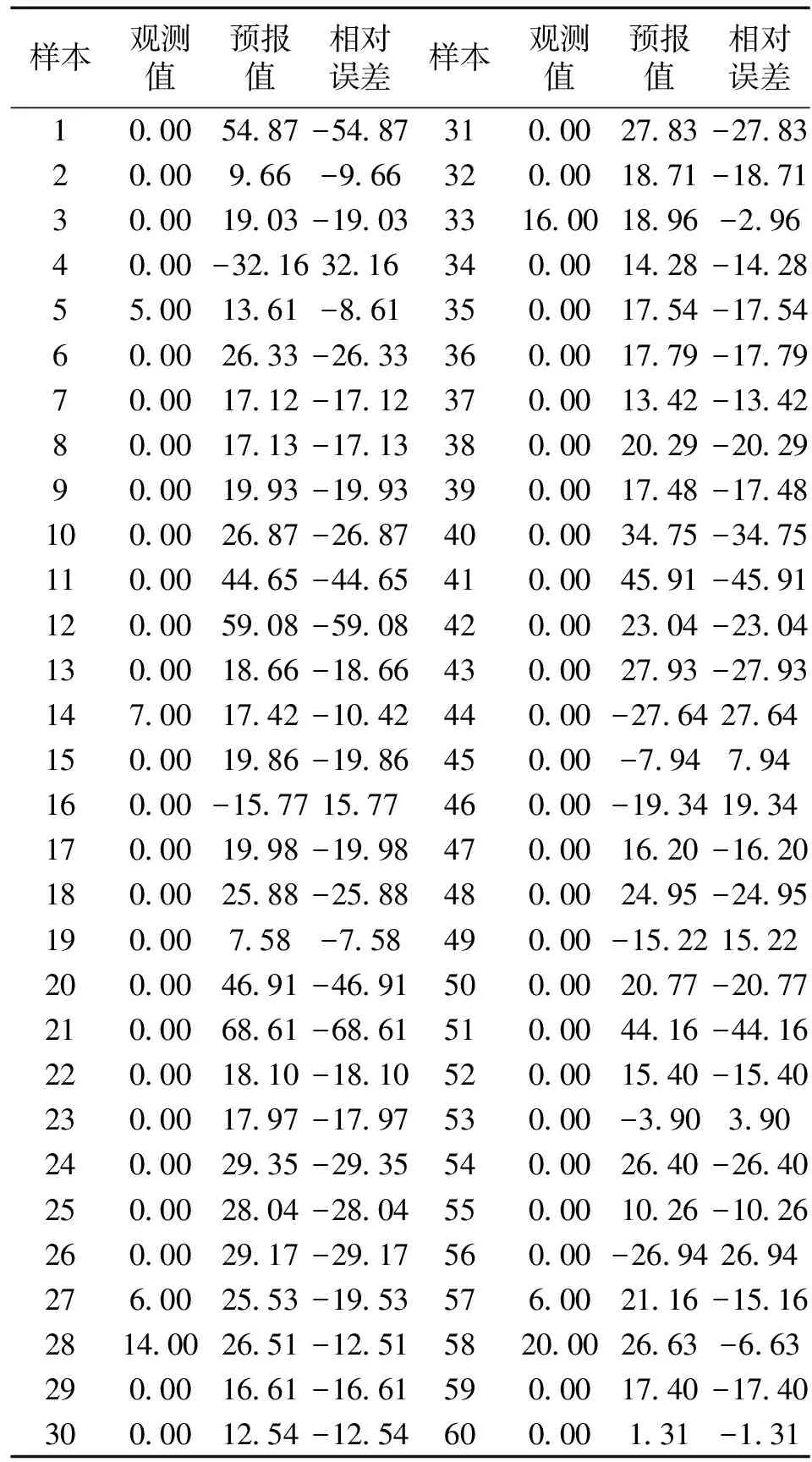
表10 12 h降水量拟合结果

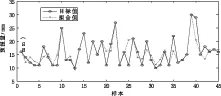
图2 6 h降水量模型拟合图

图3 12 h降水量模型拟合图

5.4 预报检验

5.4.1 逐步消空法预报模型试报 根据5.2建立的逐步消空法预报的模型，利用2011年4月1—30日的每日08时、20时的探空资料中物理指标(IQ、K指数、mK指数、SWEAT、Tg)对未来12 h是否出现强降水进行试报。实况总共是60次，大于15 mm的强降水2次，其余为弱的降水或是无降水。预报结果为试报60次，报有强降水9次，空报9次，报错2次，总共报对49次，成功率CIS=(49/9+2+49)×100%=81%。对未来6 h强降水潜势预报，实况总共是60次，大于10 mm的强降水1次，其余为弱的降水或是无降水。预报结果为试报60次，报有强降水9次，空报8次，总共报对52次，成功率CIS=(52/9+51)×100%=86%。6 h预报对比分析图略。

5.4.2 BP神经网络集成试报 根据5.3建立的BP神经网络6 h降水的参数集成和12 h参数的集成建立的网络模型，利用2011年4月1—30日的每日08时、20时的探空资料中物理指标(IQ、K指数、mK指数、SWEAT、Tg)进行试报。

6 h降水参数集成网络模型的实验结果为：试报60次，报对34次(2次强降水、32次无强降水)，空报26次，成功率CIS=(34/26+34)×100%=56%。试报结果如表11所示，网络模型预测图如图4所示。12 h降水参数集成网络模型的实验结果预报的结果如表12所示，网络预测模型如图5所示，其中报对18次(2次强降水，16次无强降水)，空报42次，成功率CIS=(18/18+42)×100%=30%。

5.4.3 预报结果小结 从以上两个预报模型的预报结果可以看出，逐步消空法建立的模型的预报成功率要高于神经网络集成的模型。6 h降水的参数集成神经网络模型预报的成功率要比12 h降水参数集成的要高。

表11 6 h降水预报结果

图4 6 h降水量的模型预测图

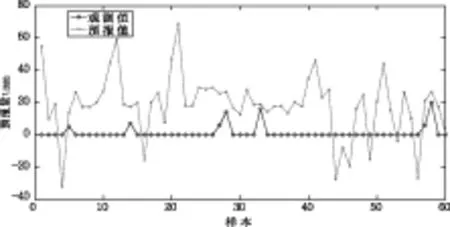
图5 12 h降水量分析的模型预测图

样本观测值预报值相对误差样本观测值预报值相对误差10005487-5487310002783-27832000966-966320001871-187130001903-19033316001896-2964000-32163216340001428-142855001361-861350001754-175460002633-2633360001779-177970001712-1712370001342-134280001713-1713380002029-202990001993-1993390001748-1748100002687-2687400003475-3475110004465-4465410004591-4591120005908-5908420002304-2304130001866-1866430002793-2793147001742-104244000-27642764150001986-198645000-79479416000-1577157746000-19341934170001998-1998470001620-1620180002588-2588480002495-249519000758-75849000-15221522200004691-4691500002077-2077210006861-6861510004416-4416220001810-1810520001540-1540230001797-179753000-390390240002935-2935540002640-2640250002804-2804550001026-1026260002917-291756000-26942694276002553-1953576002116-15162814002651-12515820002663-663290001661-1661590001740-1740300001254-125460000131-131

6 结论

本文通过对贵阳单站对流参数的相关性分析，建立强降水的预警指标的阈值，强降水指标的集成研究，得出以下结论：

①贵阳地区强降水的物理指标：IQ整层比湿积分、K指数、修正的mK指数、SWEAT强天气威胁指数、Tg对流温度。制作出相应的参数阈值，对贵阳地区强降水的潜势预报有一定的指示意义。

②逐步消空法和BP神经网络对物理指标建立预报模型，通过相同资料的预报分析，得到逐步消空法建立的预报模型优于BP神经网络的预报模型，6 h降水预报模型要优于12 h降水的预报模型。

③由于常规观测资料中，高空观测的资料每日只有两个时次，再加上贵阳的强降水量偏多等原因，强降水产生的各项物理指标与强降水的相关性也较小，产生一定的空报率，对于贵阳地区短时强降水的潜势预报还需进一步研究。

致谢：本论文在撰写方面得到高级工程师梁平的大力指导!

[1] 何立富，等.国家级强对流潜势预报业务进展与检验评估[J].气象，2011，(7)：784.

[2] 谌志刚.广东省后汛期强对流天气潜势预报方法研究[J].气象，2011，(8)：942.

[3] 刘玉玲.对流参数在强对流天气潜势预测中的作用[J].气象科技，2003，(6)：150-151.

[4] 陈秋萍，等.福建短时强天气潜势预报方法研究[J].气象，2010，(2)：32.

[5] 许爱华，等.强垂直温度梯度条件下强对流天气分析与潜势预报[J].气象科技，2006，(8)：380.

[6] http：//xj.cnr.cn/xjmlxj/xjgs/200701/t20070105_5043691

33.html.

[7] 成鹏.乌鲁木齐地区近50a降水特征分析[J].干旱地理，2010，(7)：580.

[8] 孔燕燕.寻找降雹预报指标集的一种方法逐步消空法[J].气象，2000,26(10):109-130.

[9] 金龙.神经网络气象预报建模理论方法与应用[J].北京：气象出版社，2004：3，39-47.

[10] 陆汉城，等.中尺度天气学原理和预报[M].北京：气象出版社,2004,(2):41.

[11] 朱乾根，等.天气学原理和方法[M].北京：气象出版社,2007,(2):422-426.

Heavy rainfall potential forecast method with convective parameter of the single station in Guiyang

YI Zhixue1，LAN Shihuai2

(1.Guizhou Provincial Meteorological Bureau of Guizhou Leishan county,Leishan 557100；2.Nanjing University of Information science and Technology,Jiangsu 210044)

The heavy rainfall cases of 24 hours， the heavy rainfall cases of 12 hours， and the heavy rainfall cases of 6 hours， occurring in Urumqi a station， were selected from the conventional observation datum from 2002 to 2011. By statistics and analyzing the correlation of the atmospheric temperature and humidity， stratification stability， thermal and energy physical parameter and the heavy precipitation， the result show that the correlation with the physical parameters (IQ， K， mK， SWEAT， Tg) and heavy precipitation is better. Above analyzing characteristics of physical indexes before the precipitation breaking out， occurring and after rain， the threshold value of forecasting parameters having been confirming were set with the idea of opportunity index. By using the idea of stepwise decreasing far method and the BP neural network integration， this physical parameter heaving been selecting are integrated， so the forecasting models are formed. Thus obtaining the Urumqi early warning parameters of strong convective weather forecast of potential future 6 and 12 hours， it has a certain indication role on the forecasting of rainfall Urumqi area. Through the contrast analyzing， the forecasting model to establish with the stepwise decreasing far method is superior to the integration of the BP neural network model.

Heavy precipitation； Convective parameters； Pre-warning threshold； Stepwise decreasing far method； The BP neural network； Forecasting integration

2014-07-29

易志学(1984—)，男(苗族)，工程师，主要从事天气预报工作。

贵州省青年科技基金黔气科合QN[2011]13号。

1003-6598(2015)01-0001-08

P456

A