直观图示：一种有张力的思维辅助

魏芳

大量研究表明，学生数学思维能力的差异，在很大程度上取决于学生能否将抽象的数学概念与直观的图示连结起来，取决于能否把复杂的数学问题与简单的直观图示沟通起来。笔者在日常的教学实践中，也发现了这样的现象：数学思维能力强的学生，往往能自如地借助直观形象的图示来分析思考，努力寻找数学问题的解决入口，他们的分析与沟通能力较强，数学思考的经验也更丰富。

布鲁纳关于儿童智力发展的研究表明，儿童的认知发展须要经历三个发展阶段：动作认知、图形认知和符号认知。这三个发展阶段对应着儿童思维发展的三种水平：操作水平、表象水平和分析水平。小学数学教学中，教师要充分尊重学生的认知发展规律，借助多种直观形象、具体可感的辅助手段，为学生的思维发展由操作水平逐步走向分析水平铺路架桥。希尔伯特在《几何直观》一书中谈到：图形可以帮助我们发现、描述和研究问题；可以帮助我们寻求解决问题的思路；可以帮助我们理解和记忆得到的结果。借助直观图示，可以帮助学生化抽象为具体、化复杂为简单，助推学生的思维发展。

一、 直观图示，让数的意义建构更准确

小学生的认知发展以动作认知为起点，但图形认知和符号认知也正在逐步发展。其中图形认知是动作认知与符号认知之间的中介，发挥好图形认知的媒介作用，有利于学生的认知由动作认知向符号认知发展。学生认识抽象的数，也常常要借助形象的操作或图示，以直观的方式理解数的意义。

例如，在一年级认识“20以内的数”时，借助实物图、圆圈图、小棒图、计数器等多种辅助手段，帮助学生理解“几个就用几来表示”和“十几就是由1个十和几个一组成”。引导学生经历“实物图→形象的圆圈图→抽象的数”的学习过程，逐步建立数的概念。

又如，在三年级学习“几百几十几”时，引导学生迁移前期的学习经验，借助计数器、数位顺序表等直观的图示，在“写一写，读一读”中理解更为复杂的数的意义，在“读一读，画一画”中内化对数的意义的理解。

学生在学习“小数意义”时，也是通过形象直观的图示，沟通分数与小数的联系，建构小数的本质意义。比较小数的大小时，让学生在数轴上找出小数的对应点，根据小数的位置说明大小关系。直观形象的图示为学生提供了表象支撑，也为抽象概括、分析比较提供了最为直接的意义依据。

在“数的认识”教学中，借助直观形象的图示，运用有趣又富有动感的操作，不仅能引发学生的探索兴趣，更能激起学生的积极思考与主动建构。在探索发现的过程中，强化动作认知、深化图形认知、促进符号认知，促使学生的数学思维由操作水平向表象水平和分析水平发展。

二、 直观图示，让运算的算理探索更有味儿了

学生的运算能力是在理解算理的基础上逐步形成的。在教学中，除了通过探索丰富的问题情境发展运算的含义，还要寻求合理、简捷的运算途径和运算方法。直观图示，可以具体形象地帮助学生理解运算的算理、形成基本算法，引导学生的思维逐步走向数学化。

例如，学习“9加几”时，通过实物操作初步理解“凑十”的原理，再引导学生开展“圈出10个，再填一填”的活动。在活动中，学生动手圈一圈，再次感受到“9个和1个凑成10个，7个中圈去1个还剩6个，10加6得16”。逐步形成“凑十”的表象，为学生形成算法提供直观形象的支撑，有利于算法的抽象。

又如，在学习“分数加减法”时，通过涂一涂、画一画、比一比等方法，引导学生理解同分母分数加减法的算理，具体又直观。同时也为概括“同分母分数相加减，分母不变，分子相加减”的计算方法提供表象支撑。

再如，“整数除以分数”是学习中的难点，借助直观的图示可以形象地帮助学生理解其中的算理：“1里面有2个■，4里面就有8个■”，继而把4÷■转化成4×2。再通过“分一分”“画一画”等方法，进一步探索4÷■和4÷■的计算方法，最后由学生概括算法：整数除以分数，等于整数乘以分数的倒数。

通过直观形象的画一画、分一分、算一算等活动，引导学生借助直观图示将内隐的算理清晰地展现出来，使学生不仅“知其怎样算，更知其为何这样算。”直观图示，密切了算理与算法之间的联系，引导学生的思维走向理性、深入。

三、 直观图示，让数学规律的发现更有意义

数学规律的发现与应用，也是促进学生思维发展的重要路径之一。在教学中，引导学生经历实际操作、直观图示、抽象概括等多样的活动，能够充分感悟数学规律，揭示规律本质，最终能灵活地应用规律解决问题。

例如：小红要去秋游，衣柜里有2件衬衣和3条裙子，她一共有多少种不同的穿法？

首先，学生通过动手操作试一试，寻找衬衣和裙子的搭配方法；接着，启发学生借助画一画的方法有序地表示出6种不同的搭配方法（如图1）；最后，引导学生探索其中的规律。多样活动之后，学生自然积累起这样的思考经验：第1件衬衣可以配3条裙子，第2件衬衣也可以配3条裙子，一共有2个3种搭配的方法。同样，部分学生也会这样思考：第1条裙子可以配2件衬衣，第2条裙子可以配2件衬衣，第3条裙子也可以配2件衬衣，一共就有3个2种搭配的方法。直观形象的图示，把衬衣与裙子的选配过程清晰地呈现了出来，沟通了选配方法与乘法意义之间的联系，搭配中的规律呼之欲出：衬衣的件数×裙子的条数=搭配方法的种数。

又如，“一条走廊长24米，每隔3米放一盆花。要放多少盆花？”其中，放花的情况又可以分为三种：两端都放、两端都不放、一端放另一端不放。借助直观图示，“段数与盆数之间的规律”具体清晰地展现出来：

（1）两端都放：

24÷3=8（段） 8+1=9（盆）

（2）两端都不放：

24÷3=8（段） 8-1=7（盆）

（3）一端放另一端不放：

24÷3=8（段） 8段=8盆

通过比较与分析，学生不难找出其中的规律：两端都放花，盆数比段数多1；两端都不放花，盆数比段数少1；一端放另一端不放，盆数等于段数。形象而直观的图示，不仅使学生理解了“摆花”的三种情况，即规律所蕴含的本质内涵，也使学生真切感受到画图在探索规律中的作用，为后续的应用积累了借助图示思考的经验。直观图示能为抽象概括规律提供最直接的桥梁，使抽象的数学问题形象化，使学生能真正理解规律的本质，并能运用规律来解决问题。

四、 直观图示，让数量关系更清晰明

学生解决问题的关键，是要建立已知条件与所求问题之间的联系，而很多实际问题中条件与问题之间的关系并不直接相关，这就要求学生具有一定的分析能力，寻找隐藏于条件中的相关因素。直观图示就是非常好的辅助手段，往往能帮助学生找到条件与问题之间的联系，从而利于学生思考解答。正如信息加工理论的学者所言：有了正确的表征，问题就已经解决了一半。

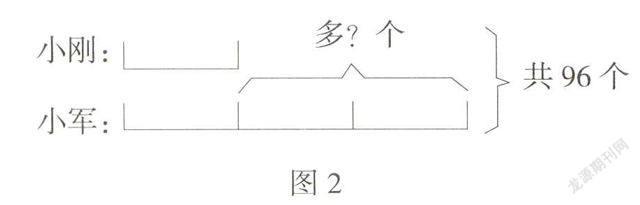
例如：小军和小刚共摘苹果96个，其中小军摘的数量是小刚的3倍。请问小军比小刚多摘多少个苹果？

对于三年级的学生来说，这样的问题具有一定的难度。因为要求“小军比小刚多摘多少个苹果，先要知道小军和小刚分别摘多少个苹果”。可是题目中两者都是未知的，只有“小军和小刚摘苹果的总数”，和“他们摘苹果数量的倍数关系”。能否在这两个条件之间建立联系就成了解决问题的关键。通过画示意图，数量之间的关系一目了然：

根据线段图，数量之间的关系逐渐清晰：96个苹果对应着“1+3=4份”，“96÷4=24个”就是其中一份的个数，也就是小刚的个数，“24×3=72个”是小军的个数，“72-24=48个”就是小军比小刚多的个数。通过观察直观的线段图，有的学生还发现：小军比小刚多的个数，就是其中2份的个数，所以还可以直接用“24×2=48个”来解答。正是由于直观图示的帮助，学生才能够正确地沟通问题与条件之间的本质联系，使看似无从下手的问题变得可以捉摸，也使复杂的数学问题简单化。

应用直观图示的策略，对于学生学习数学来说是非常重要的。随着年级的升高，解决问题经验的积累，学生会逐渐感受到直观图示的价值。它不仅可以帮助学生沟通相关条件与问题之间的联系，同时也能把一些隐含的关系层层凸显出来，助推学生顺利地解决数学问题。

五、 直观图示，让知识体系的架构更完整

维果茨基认为，学习的本质是以模仿为基础的沟通过程；在学生最近发展区框架内，模仿并不是消极的，它同样具有建构的意义。数学知识的发展遵循由易到难、由浅入深的原则，在教学某一类数学知识时，注重知识发生发展的来龙去脉，侧重于横向化。随着年级的升高，某一类数学知识又会逐步深化，就要逐步关注纵向的数学化。缺乏系统沟通，数学知识就像一盘散沙，无法提升，也无法灵活应用。

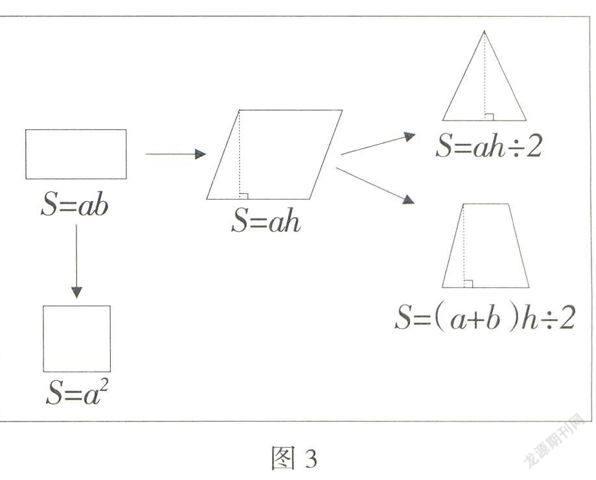
例如，在平面图形面积计算的复习中，可以组织学生对已经学过的长方形、正方形、平行四边形、梯形、三角形等的面积计算方法进行纵向梳理，边借助直观图示边回忆面积计算的方法，通过结构图把所学平面图形的面积计算方法进行有序的沟通，揭示相关图形面积计算之间的联系与区别。

又如，在复习长度单位之间的进率时，可以引导学生沟通已学单位之间的关系，用形象直观的图示梳理，帮助学生厘清相关单位间的进率，建构完整的认知结构。借助直观图示梳理长度单位的经验，又将存在于学生的经验系统中，推广至面积单位、体积单位间的进率结构中。

直观图示，有时可以是廖廖几笔，也可以是圈圈画画；有时是横向梳理，也可以是纵向架构。多样的方法不仅可以使抽象的数学知识直观化，也可以使抽象的算理形象化，更可以把内隐的规律外显化。直观图示的辅助，能够帮助学生进行数学思考，获得真正的数学理解，继而积累丰富的数学活动经验。

【责任编辑：陈国庆】