发现数学价值 发展学生学力

【摘 要】基于5节初中数学展评课的观摩，其共同特点是教学目标有机融合、情境创设指向合理、教师引导作用明显、数学应用价值得以凸显、学生学力发展有所体现。但从展评课的主题来看，课堂教学中数学学科价值有待发掘、学生学力发展有待深化，以此促进初中数学教学正向发展。

【关键词】初中数学 教学评析 数学价值 学力发展

江苏省第十届“杏坛杯”苏派青年教师课堂教学展评无锡分赛区活动于2015年4月12～14日在江苏省南菁高级中学实验学校举行，笔者有幸担任数学组评委，共观摩了5位初中青年数学教师的课堂教学，课题分别是“图上距离与实际距离”“几何中的一题多解”“平均数（两位教师执教）”“反比例函数”。

本文结合5位青年教师的课堂教学，从共同特点和问题建议两个方面作一些述评，以期更好地促进青年教师课堂教学技艺的提升。

一、共同特点

5位教师基本都在大市层面获得过基本功或优质课评比一等奖，具有扎实的教育教学基本功，课堂教学都能紧扣本次展评活动的主题“发现学科价值，发展学生学力”，较好地展现了苏派青年教师的教学风采。主要特点有：

1.教学目标有机融合

我们知道，课堂教学的本质就是要使学生得到全面、和谐、持续的发展，在学生获得知识、形成技能的过程当中，发展学生的过程性目标。从某种意义上来说，“知识技能的学习必须以有利于其他目标的实现为前提”。正如雅斯贝尔斯所言，“教育过程首先是一个精神成长过程，然后才成为科学获知过程的一部分”。对课堂而言，教学应努力体现教学内容中所含的丰富的学科价值。纵观5节课，他们不仅关注知识与技能的达成，更为重要的是关注到了其中所蕴含的思想和方法，以及学生能够获得的基本活动经验。

比如，“图上距离与实际距离”的教学，让学生在经历观察、操作、探索、对比等学习过程中，体会数学的实际应用价值；“几何中的一题多解”在学生探索多种辅助线的添法基础上，很好地发展了学生的思维，并揭示蕴含于解题方法之中的数学思想方法；“平均数”的教学则不是仅在“加权平均数”的计算方法上兜圈子，而是极力渗透统计意识以及注重数据处理能力的培养；“反比例函数”的教学则紧紧抓住“对应”的思想，让学生充分理解反比例函数的本质，而非一般意义上的形式认知。应该说，这5节课都能把“过程方法”、“情感态度”的目标与“知识技能”目标有机地融合成一个整体。

2.情境创设指向合理

苏科版初中数学教材主编杨裕前说过，一个好的情境应具有以下几个特征：一是学生所熟悉的；二是要简明的、真实的、合理的；三是能尽快将学生引向所要学习的知识本质。在2006年全国青年数学教师的评优课上，笔者聆听了“线段、射线、直线”一课，执教者引导学生做了两个游戏，至今记忆犹新。游戏一：教师让1名同学站起来，然后说“与他在一条直线上的同学站起来”，学生站起1个、2个、3个……他们迟疑地、陆续地站起；游戏二：教师让两名同学同时站了起来，然后说“请与这两名同学在同一条直线上的站起来”，学生冲动地站起来、又坐下……这样的简单活动情境，就将知识的本质很好地揭示了出来，且恰到好处，真正地使创设的情境起到了“承重墙”的作用，而非徒有华丽外表的“装饰”。

在本次展评活动中，情境创设也是匠心独具。比如，让学生观察常熟到江阴、住宿地到学校的两张地图，直观地引入“图上距离与实际距离”这一课题；给学生讲推销员推销梳子的几种不同方法，并给出导致的不同结果，以此说明思维的重要性，巧妙地引入“几何中的一题多解”这一课题；通过播放视频，让学生给视频打分，给出应聘数学教师几项素质测试成绩，让学生确定录取谁，这样就很自然地引入“加权平均数”这一课题；通过汽车从南京到上海的行车速度、时间、路程三者之间的关系，顺利地引入“反比例函数”这一课题。

3.教师引导作用明显

众所周知，课堂教学中教师的功能角色是学习活动的组织者、引导者、合作者。这种理念，实际上并没有贬低教师在课堂教学中的地位和作用，甚至是，教师的作用还得到了加强。不是吗，自实施新课程以来，我们大部分教师已经在实践当中深深地感到责任以及任务比过去重了，因为讲什么东西给学生听，对很多教师来说是“驾轻就熟”的，但要让学生自己想办法弄懂这些事情达到“自明”，你就要去不断地引导他们，组织他们开展活动，不断地给予点拨、启发，这比教师自己讲清楚一件事情可能更难。这大概就是“教育的本质在于唤醒”的要义所在吧。

本次展评课中，教师的引导作用体现在让学生经历探究新知的过程中。比如说，测量两张地图中的相关线段的长，让学生自悟“比例尺”的意义；研讨一个几何图形辅助线的不同添加方法，让学生养成敢于尝试的习惯以及发展发散思维；提供素质测试的两组数据，让学生在“平均成绩不同”和“平均成绩相同”的认知冲突中主动思考如何处理数据和分析数据，从而暴露“加权平均数”的知识产生过程，间接地强调了“加权平均数”的必要性；从若干实际事例，如“路程一定，时间和速度之间关系”“面积一定，长与宽之间关系”等实际问题的探究，让学生自觅“反比例函数”的基本特征等等。

4.应用价值得以凸显

数学的应用价值，一方面体现在用以解决数学内部的一些问题，这归属于浅层次或是表层的应用；另一方面体现在应用于数学基础知识以外，是深层次的应用，反映数学的思维、思想和方法。数学内部应用，即关于“双基”训练的问题，传统教学关注得似乎有点“过了头”，现在再谈“双基”又似乎让人觉得有点“老土”的味道。其实不然，新课程背景下的课堂教学同样要关注“双基”，要注意的是：其一，基本技能的形成需要一定量的训练，但不能简单地依赖“熟能生巧”，要注重训练的针对性、科学性；其二，大量的训练，也会使学生的一些不良行为习惯得以强化，以至于“熟能生笨”；其三，技能的形成和熟练，依据学生的年龄特征和心理特点，具有阶段性，要循序渐进；其四，在技能训练中，要注意引导学生加深对相应知识的理解，不能远离本原性知识而进行“按部就班”的操练。

这里要说明的是，本次展评的5节课更加凸显数学的深层次应用。比如，“已知三条线段长分别为2、3、4，添加一条线段，使这四条线段为成比例线段”，体现了发散性思维的应用价值；一题多解中不同辅助线的添加方法，最终却“殊途同归”，揭示了“建立未知与已知之间关系”的核心价值；通过计算平均身高，揭示计算平均数的多种方法，反映了数学应用的适用性价值；呈现反比例函数的三种形式，反映了数学应用的变通性价值等等。

5.学力发展有所体现

所谓学力，是指学习者借助一定的教育环境、教育资源和积极的教育实践活动所形成的自我获取、自我建构、自我发展、自我超越的知识、态度、能力的总和。纵观本次展评的5节课，都或多或少地注重了学生的学力发展，不仅发展了基础性学力，也关注了发展性学力和创新性学力的发展。比如，从等积式到比例式的变式，发展了学生等价转化的学力；从多边形到三角形再到平行线之间的沟通，发展了学生类比转化的学力；招聘方案的合理设计，发展了学生创新设计的学力；对学生阅读课本的方法指导，发展了学生阅读的学力；反比例函数不同形式之间的变通，发展了学生辨析的学力等等。

二、问题建议

教学是遗憾的艺术，十分完美的课堂严格意义上来说不是一个好课堂。本次展评的5节课虽有很多可圈可点之处，但也还存在着一些问题。这里不谈一般意义上的课堂教学问题，仅围绕本次活动的主题“发现学科的价值，发展学生的学力”谈需要把握的两个问题。

1.数学的学科价值有待发掘

数学是思维的体操，数学是科学的语言。法国数学家拉普拉斯的名言说“数学是一个卓绝的工具”，法国另一位数学家笛卡儿进一步阐释“数学是知识的工具，亦是其他知识工具的源泉”，它是“自然科学的皇后”“思维艺术的体操”“世界之美的原型”。学好数学，能让人更加聪明、更有智慧、更为精细、更具力量。

透过这些名家的论述，我们可以发现，数学不仅具有工具价值，还具有应用价值；不仅具有理性价值，还具有审美价值；不仅具有科学价值，还具有人文价值。在数学课堂教学中，就需要充分发掘这些价值，并适时渗透，才能是具有“数学味”的课堂教学。比如说，“图上距离与实际距离”的引入教学中，教师可适时追问，“这两张地图是怎么制作出来的？”以此引导学生思考，去发现隐藏于其中的数学，渗透数学的工具价值。再比如，“反比例函数”的教学，更应突出在实际生活中反比例函数模型的应用，体现数学的应用价值。还比如，教学中要让学生因为“数学好玩”而感受到生活的丰富多彩，激发数学学习的内在动力，以此凸显数学的人文价值等等。

2.发展学生的学力有待深化

关于学力发展，笔者想起2006年岁末去山东省聊城市茌平县杜郎口中学的调研学习，这一次活动与其说是领略了我理想中的好课“风采”，倒不如说是让笔者见证了“学生学力发展”是如何在课堂教学中得以实现的。在杜郎口中学的课堂教学中，没有传统课堂中教师的“侃侃而谈”，闪现出来的是学生智慧之火花，教师在教学过程中设置很多问题情境，师生之间、生生之间有问有答，或讨论或交流，教师将课堂组织得“热闹非凡”，将学生调动得“兴趣盎然”，“以人为本”在这里得到了具体的体现，“关注生命”在这里得到了有效的落实，“双基训练”在这里到边到位，“综合素质”在这里得到锻炼和发展！

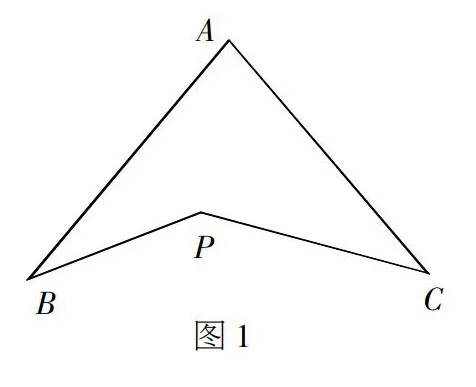
反观本次课堂教学展评的5节课，虽然在学力发展上执教者也有所体现，比如有一个教师布置的作业是“把今天上课的感受写成一篇数学小文章”，就别具一格，让学生写出感悟可谓是发展学力的一个有效载体，但总体感觉还有进一步深化的余地。比如说，“已知■=■，且x+y=24，求x、y的值”，采取的是设k法，但问题是为什么想到“设比值为k的呢”？教师如果能启发学生思考，找到“比例尺”这一源头，就达到“不仅知其然，而且知其所以然”的效果，无形之中发展了学生的学力。再比如，“如图1，已知∠A=80°，∠B=30°，∠C=35°，则∠BPC= ？”在教师的引导和启发下，学生探究出一般结论：∠A+∠B+∠C=∠BPC。到此就结束了，但笔者感觉还“意犹未尽”。如果教师能进一步引导学生思考：连接BC，如果点P在△ABC的边BC上这一结论还成立吗？如果点P在△ABC的外部呢？这样一来，就变成了一个动点探究问题，学生学力的发展也就接了“地气”。

（作者单位：江苏省连云港市教育科学研究所）