寓评于赏，寓赏于介

【摘 要】“通过写作来学习”在数学教学中开展几年来，得到学生的喜欢、家长的肯定，也有效促进了学生对数学的深入反思与深刻理解。特别是针对学生数学写作开展的“链接式点评”，更是激发了学生的写作兴趣和对数学的学习热情。针对展示的数学写作和点评案例，一方面追求“寓评于赏”，在赏析中“激励、唤醒和鼓舞”，另一方面又“寓赏于介”，在推介中“打开一扇窗”。

【关键词】数学写作 链接式点评 寓评于赏 寓赏于介

文汇新民报业高级记者翁思再先生在一篇散文中提及，寓评于赏，寓赏于介，这是前辈传给文艺部的特稿写作口诀，这也逐渐成为笔者的一种写作和叙事习惯。联想到我们开展的数学写作研究，如何写好学生写作的链接式点评，对“寓评于赏，寓赏于介”心有同感。下面先展示新近积累的数学写作与链接式点评案例，然后给出一些思考，与大家研讨。

一、案例展示

案例1

“不恰当举例”出错一例

七年级 张睿

“有理数”单元测试卷上有一道填空题，虽然只有寥寥几笔，却让我栽了个大跟头（丢掉了满分）：

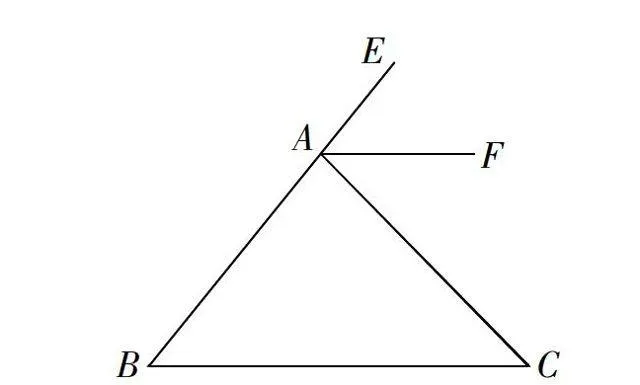
我刚开始举例就举错了，没有符合题意a

这道题让我知道：解题时最好要一次性做对，但也要重视检查。有时不能只靠第一感觉，也不能只靠一次的举例。

链接式点评：这篇习作虽然短小，但是值得说说的话题却不少。

第一，七年级学生应该知道“两个负数，绝对值大的反而小”。就这道考题来说，小睿同学初始错误的本质就出在对两个负数大小的误解，这是后续错误的根源。

第二，学会举例，重在举出恰当例子。进入初中数学学习，很多概念的理解、性质的概括、问题的求解，都需要学会举例，能否举出恰当的例子，往往是问题快速突破的关键。

第三，学会校对，提倡从不同角度验证。如小睿同学所说“解题最好一次性做对”，但是对于限时独立完成的考试来说，也要重视必要的检查，检查需要从不同的角度来验证，而不是在原有思路上“再算一遍”，因为人们往往有思维定势。那么什么是从不同角度来检查呢？我们认为，平时在问题求出答案后加强回顾反思，反思还有没有其他的解法，就是训练自己从不同角度检查的能力。小睿同学在文中最后那句“也不能只靠一次的举例”表达的也是这个“多样验证”的意思。

案例2

订正三次，只为规范表达吗？

——对一道题目订正的反思

七年级 朱云清

今天的课堂作业，一个很简单的习题，我却被要求订正了三次，而且老师还让我把三次订正内容都写在黑板上，进行讲解，最终我才发现：原来不只是为了规范表达。

习题：如图，AF平分△ABC的外角∠EAC，且AF//BC，试问∠B与∠C的大小关系如何？

从第一次到第三次的修正，证明步骤一次比一次规范，如果不是这次订正，我还没有意识到前两次我的几何证明步骤是如此的杂乱无章，可见，以后对于这种题目还得多加训练，让自己以后处理这种题目游刃有余。

链接式点评：由于七年级对于几何证明要求不高，加上小学阶段只要求学生对图形有直观的认识，对严格表达或规范组织几何推理语句的要求不高，所以像小朱同学这样明了问题的思路后，前两次的语句组织都有“跳跃”，不够严谨，直到第三次才优化完整。需要指出的是，这并不仅仅是规范表达的教条主义，而是有更多的意义，最重要的并不是应试时不丢分，而是获得几何学习带来的“理性震撼”。初中阶段的平面几何源于两千年前的《几何原本》，这本几何学著作的价值就在于从简单的公理出发，以无懈可击的演绎推理得出很多图形的性质，这个推理过程，使人感受到步步有据的理性力量。这事实上也是东西文化、文明的一种差异。

案例3

“捉-放-捉”：感受样本估计总体思想

七年级杨琦

教材上安排了“实验与探究”，老师提前一周就布置同桌两人带一瓶豆子，供数学活动课上开展数学实验。数学课上也进行实验，对我们来说很新鲜，所以大家都期待着数学实验的到来。

终于到了这节数学实验课，我们两人一小组，按照课本上的程序操作：

（1）从瓶子中取出一些豆子，我们小组数出这些豆子的粒数m=12；

（2）给这些豆子做上记号；

（3）把这些标识记号的豆子放回瓶子中，充分摇匀；

（4）从瓶子中再取出一些豆子，数出粒数p=16，其中带有记号的豆子的粒数n=4；

（5）估计原来瓶子中豆子的粒数q≈4×12=48；

（6）数出瓶子中豆子的总数为51。

结论：我们的估计跟总数比较接近。

老师让几个小组向全班同学做了汇报，其中我们小组的实验结果估计出来的总数最接近总数，而有些小组实验后的估计却偏离总数很严重，这是什么原因呢？

原来，他们有些小组带了一个小瓶，只装了不到30粒豆子，也就是总数太少；有些小组虽然带来的豆子数量较大，但是在第三步操作时，没能“充分摇匀”，所以也出现较大偏差。看来实验也不是好做的呀，受到影响的因素太多了。现在想想宇航员王亚萍在太空为我们演示实验时，一定付出了更多的努力和智慧。

链接式点评：上面的实验实际上是生产和科研中经常用到的“捉-放-捉”的方法，该方法体现了样本估计总体的思想，实际中常用它估计一个总体的数量。值得一说的是，数学实验也是数学学习的重要方式，通过数学实验往往能生成特殊、发现奇异、估计性质、猜想方向，对数学上的发现、发明以及难题求证有重要作用。但是如上文这样，数学实验也需要像科学实验一样，注意实验条件、环境，任何细节的疏忽都会影响实验效果。

二、寓评于赏，寓赏于介

1.寓评于赏，在赏析中“激励、唤醒和鼓舞”

“教育的奥秘不在传授，而在激励、唤醒和鼓舞。”正如第斯多惠所言，对学生数学写作的点评也要坚持赏析第一，赏析中注重对学生的激励、唤醒和鼓舞。以笔者的点评经验来看，学生对教师写在他们数学习作后面的点评意见总是非常看重，会反复阅读；对发布在博客上的在线点评总会跟帖或转载。以“案例1”中笔者对小睿同学的点评来说，在点评中的赏析绝不能流于空泛，要言之有物，有凭有据地赏析才能真正打动和鼓舞学生。

2.寓赏于介，在推介中“打开一扇窗”

近读郑毓信教授、罗增儒教授等国内知名数学教育学者的文章，他们对课例的赏析往往并不止于就事论事，而是由一段课例或片断出发，把故事讲述得形象而生动，使阐释的观点独到而深刻。受到启发，笔者在点评学生写作时，也注意捕捉学生作品中某个片断或观点，由此展开、链接或拓展，推介相关的知识、方法或数学史话，收到了较好的效果。以“案例2”来看，在小朱同学多次订正后，要求他写出三次订正的经历，在参与拟定标题“三次修正，只为规范表达吗？”时，就想着要以此文为契机在点评中推介数学史话、传递“理性震撼”。在“案例3”的点评中既推介“样本估计总体”思想，强调重视“捉-放-捉”的实验方法及注意事项，同时又肯定了数学实验在数学学习中的重要性。当然，上述努力都是想由学生写作出发，为学生“打开一扇窗”，引导他们透过窗户眺望远方。

据笔者调查，“通过写作来学习”已经得到不少一线教师的关注，有些同行在自己的博客、QQ空间里常常发布学生写作的案例，引发读者纷纷点赞、分享、评价、转载，尽管有些点评还少些独到、深刻，但是他们“在路上”的精神已感动和影响了很多师生的实践跟进。清代数学家华蘅芳初涉微积分时“反覆展玩不辍，乃得稍有头绪”，他作了一个精彩的比喻：“譬如傍晚之星，初见一点，旋见数点，又见数十点、数百点，以致灿然布满天空。”想来数学写作的点评过程也可以描述为对学生写作的扶持并使之渐次丰满的过程。

【参考文献】

[1]翁思再.之江教我写新闻[N].新民晚报，2014.4.15（A28）.

[2]李秉彝，潘荣菲译，黄兴丰校.展望新加坡2013年中学数学课程[J].数学教学，2012（08）.

[3]张奠宙，郑振初.“四基”数学模块教学的构建——兼谈数学思想方法的教学[J].数学教育学报，2011（20）.

[4]汪晓勤.陈年佳酿[J].数学文化，2013（4）.

（作者单位：江苏省海安县城南实验中学）