对一节同课异构课的“CT”扫描

在一次几何教学专题教研中，我们安排了四位教师同课异构《线段、角的轴对称性》第一课时。在听课反馈中我们采用了类似于医学检验中的“CT”扫描法，各位听课、授课的教师畅所欲言，对这一课时的教学组织案例分了四个横断面进行扫描和研讨。

横断面一：线段的轴对称性结论的得到

为得到结论1：线段是轴对称图形，结论2：线段的垂直平分线是它的对称轴，四位教师探究活动可分为以下两类。

[Ⅰ类]1.猜想：线段是轴对称图形

2.活动：每位同学拿出一张薄纸，在纸上画一条线段，对折

3.观察：折痕有什么特殊的几何特征

4.发现：折痕是线段的垂直平分线

5.验证：设折痕PQ交线段AB于点O，因为对折重合，所以OA=OB，∠POA=∠POB=90°

6.结论：线段是轴对称图形，线段的垂直平分线是它的对称轴

[Ⅱ类]1.活动：每位同学拿出一张薄纸，在纸上画一条线段AB，作线段AB的垂直平分线l，交AB于点O，把OA沿直线l翻折

2.发现：OA与OB重合

3.验证：因为直线l垂直线段AB，所以∠1=∠2=90°，所以把OA沿直线l翻折，与OB在同一条射线上，又因为OA=OB，所以OA与OB重合

对Ⅰ类活动设计的几个疑问：

1.为什么对折线段AB？（实际上已经默认了线段是轴对称图形，只要端点A、B重合就是对折，这是拿着第一个结论去导出第二个结论）

2.端点A、B怎么就能重合？如果不是薄纸，端点A、B怎样确保重合？（教师可帮助学生回忆针孔法）

3.全班同学画出的只是具体线段，能穷尽所有线段去折叠去验证吗？

对Ⅱ类活动设计的几个疑问：

1.为什么作线段的垂直平分线而不是其他的直线？（活动的指向性太强，终究是知识的传递）

2.学生通过找中点画垂线的方法精准吗？（本节教材中给出的两个练习很好地规避了这个问题）

重新思考：Ⅱ类活动并不是真正意义上的活动，还仅仅是知识传授（活动中指定作线段的垂直平分线），弱化了学生数学思考的培养。Ⅰ类活动设计是有效活动，但仅有活动Ⅰ就得到结论是不严密的，教师应引导学生认识到，“线段的垂直平分线是它的对称轴”的活动经验是基于假设获得的，我们不可能通过反复实验验证它的正确性，但可从全班同学的活动中抽象出线段的垂直平分线的概念，教师进而再引导学生反思：线段的垂直平分线为什么是线段的对称轴（有学者称之为“自反抽象”），以此为直接对象，进行推理，这样由浅入深得到了知识，从而培养学生认识具体与抽象、特殊与一般的辩证关系。

扫描结论：经验不能代替知识，但经验可以转化为知识。

横断面二：线段垂直平分线性质定理的得到

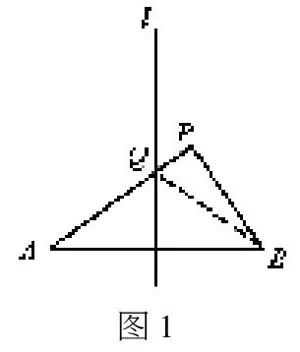
给出问题：线段AB的垂直平分线l交AB于点O，点P在直线上，PA与PB相等吗？为什么？四位教师在课堂上都设计了组内交流环节，学生展示的成果有：度量法，圆规截取比较法，证明图形全等，翻折重合。

重新思考：教学中还要引导学生认识，用度量法和圆规截取比较法得到的结论都只是活动中的经验和猜想，会有误差，需要得到证明。对称是一种全等变换，因此教学中可以不具体呈现直角三角形全等的证明，而是将教学重点放在利用线段的轴对称性进行合情推理上，激发学生对“变换几何”的价值认同——运用图形的运动研究图形的性质。

扫描结论：发展学生的合情推理和演绎推理同样重要。

横断面三：线段垂直平分线外的点到线段两端距离不等的得到

教师首先引发学生思考：不在中垂线上的点P还具备“到线段两端距离相等”这样的性质吗？学生通过目测或度量，发现不相等。然后引导学生采用化归的方法，将未知的、较为复杂困难的问题转化为已经解决或较容易解决的问题。

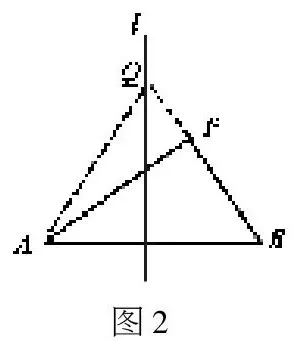
重新思考：“化归法的核心思想是代表了相反方向上的思考和转化”。这里具体的反方向转化就是将点P“反转到”中垂线上的点Q（见下图），学生理解了这样的转化后，证明就水到渠成了。对于后续学习圆周角性质定理，学生也就不难理解将圆外（内）角反转化为圆周角了。

扫描结论：从“广度”与“深度”上研读教材，深入浅出。

横断面四：教材中两个练习题的处理

第1题是数学内部的知识应用：利用网格线画线段PQ的垂直平分线;第2题是数学外部的知识应用：在公路旁设一个公共汽车站，设在什么地方，才能使A，B两村到车站的距离相等？有教师将第2题作为问题引入，最后解决这个问题实现首位呼应。

研讨中教师有两个疑惑：练习1的价值是什么？练习2的解决似乎用了第二课时的定理“到线段两端距离相等的点在线段的垂直平分线上”。

重新思考：尺规作线段的垂直平分线的理论依据是到线段两端距离相等的点在线段的垂直平分线上，本节课上是无法完成的，但是利用网格线能准确找到线段中点并作垂直（回顾旧知），练习1使学生明白网格是作线段垂直平分线的有效工具，对今后在平面直角坐标系中研究几何图形有帮助。练习2是培养学生的逆向思维，它的正确性就在于命题“线段垂直平分线上的点到线段两端的距离相等”（纯粹性）和它的逆命题（完备性）都是真命题，所以有了线段垂直平分线的“集合”定义：{P│点P到线段两端距离相等}，这样的设置起到承上启下的作用。

扫描结论：理解习题的设计价值，触类旁通。

以上扫描的四个横断面合成了一个完整的“关联式”活动：发现并证明线段的轴对称性，利用它推导出线段中垂线的性质，运用和巩固中垂线的性质。教学中要充分发挥每一个活动的价值，实现新课程标准中要求的“四基”的有效达成。

作者单位：江苏镇江市教研室