基于Excel平台的时间数列长期趋势模型的建立

【摘要】通过实例说明在Excel平台上建立时间数列长期趋势模型常用的方法和步骤，进一步说明了Excel是一款集表格处理、数据管理、统计制图、统计分析于一体且实用性强操作简单方便的办公软件。

【关键词】Excel平台 时间数列 趋势模型

【资助项目】广西高等教育教学改革工程项目立项2014JGA209。

【中图分类号】G64 【文献标识码】A 【文章编号】2095-3089（2015）01-0222-02

时间数列长期趋势模型的测定就是根据时间数列中指标值的发展变化趋势，配合一条理想的趋势线，从直观上看，这条趋势线要离各散点最近。本文将通过实例说明如何在Excel平台上实现时间数列曲线趋势模型的建立。

1.时间数列长期趋势模型的选择

时间数列长期趋势模型的选择可以根据时间数列的分析指标来确定，当数列指标值的一级增长量大致相等时，应选直线模型；二级增长量大致相等时，应选二次曲线模型；环比发展速度大致相等时，应选指数模型。

2.趋势模型中未知参数的确定

趋势模型中未知参数的确定最常用的方法是最小二乘法，即时间数列指标值与相应趋势值的离差平方和最小。

2.3模型为yt=abt时，对上述方程兩边取对数得：lny=lna+tlnb令lny=Y，lna=A，lnb=B则即可化为2.1的情形。

3.基于Excel的时间数列长期趋势模型的建立

3.1直线趋势模型的建立

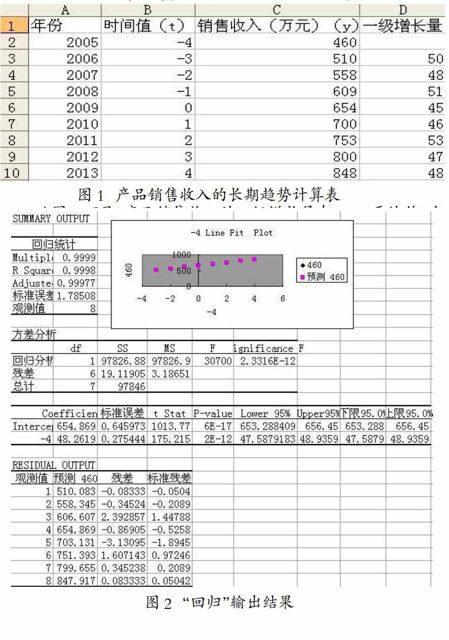
例1 设某企业2005—2013年的产品销售收入资料已输入到Excel工作表中（图1）。求销售收入的趋势模型。

图1 产品销售收入的长期趋势计算表

从图1可见，产品销售收入的一级增长量在48.5（平均值）左右，所以可配合直线趋势。

在Excel的数据分析工具中，有一个专用于进行回归分析的工具。使用此工具，可以更加方便快捷准确地进行回归分析，并能提供更多的数据信息。

第一步，用鼠标点击工作表中待分析数据的任一单元格，选择“工具”菜单的“数据分析”子菜单，用鼠标双击“回归”选项，进入回归对话框。

第二步，在回归对话框中，在“y值输入区域”框中输入C2：C10，在“x值输入区域”框中输入B2：B10，选中“标志”复选框，在“输出区域”中输入A12，选中“残差”、“ 标准残差”、 “线性拟合图”等复选框。

第三步，单击“确定”按钮，即在以A12为起点的右边空白区域给出结果（图2）。

图2 “回归”输出结果

结果表明，趋势方程为：yt=654.87+48.26t

从判定系数看，在时间对产品销售收入的影响中，有99%可由该回归方程解释。从t检验看，截距项和回归系数的p值都远远小于0.05，表明二者都是显著的。从F检验看，Significance F为2.3316E-12，表明该模型通过了5%的显著性检验，模型整体也是显著的。所以回归方程是合适的。

3.2曲线线趋势的建立

例2 设某企业1996—2013年某产品产量资料已输入到Excel工作表中（图3），求该产品产量趋势模型。

3.2.1计算时间数列指标值的二级增长量

单击D3单元格，输入“=C3-C2”，回车后得第一个逐期增长量为26，移动鼠标箭头至D3单元格右下方使其变为“+”号，按住鼠标左键向下拖拽，至D18单元格放开鼠标，即可得1996-2013年的逐期增长量。类似前面作法可得所有的二级增长量。从图3中可看出，企业产品产量的二级增长量大致相等，可以拟合抛物线趋势模型。

图3某企业1996—2013年产品产量相关数据

3.2.2用常规方法建立二次曲线回归方程

第一步，单击F2单元格，输入“=B2？鄢C2”，回车后得第一个xy值为-1608，类似3.2.1作法，即可得1996-2013年的xy值。同样依次算出1996-2013年的x2，x2y，x4值。

第二步，单击B19单元格，输入“=SUM（B2：B19）”，回车后得■x值为0，类似算出■y，■xy，■x2，■x2y，■x4的值。

第三步，将上述各合计值代入方程组（2）解得a=970.29，b=178.7，c=10.38，即回归方程为yx=970.29+178.7x+10.38x2 。

若要用此方程求各年的趋势值，可以单击J2单元格，输入“=970.29+178.7？鄢B2+10.38？鄢E2”，回车后得1996年预测值为205.01，再算出1997-2013各年预测值。从图3中可看出，各年预测值与实际相差不大，说明回归方程的代表性是很高的。

3.2.3 用“添加线性趋势线”建立二次曲线回归方程

第一步，拖动鼠标选定数值区域B2：C18，不包括数据上面的标志项。

第二步，选择“插入”菜单的“图表”子菜单，进入图表向导。

第三步，选择“图表类型”为“散点图”，然后单击“下一步”。

第四步，继续单击“下一步”，选择“标题”下的子项“图表标题”，在其中输入“产量与时间”，在“数值（X）轴（A）”子项中输入 间”，在“数值（Y）轴（V）”子项中输入“产量”。单击“完成”，即生成散点图。

第五步，在散点图中，用鼠标对准任一数据点，单击右键，选择“添加趋势线”，在“类型”选项卡中选择“多项式”，阶数选择“2”，在“选项”选项卡中单击“显示公式”和“显示平方”复选框，再单击“确定”即可得添加线性趋势线的结果，如图4 。

图4添加线性趋势线结果

结果表明所求的回归方程也是：yx=970.29+178.7x+10.38x2

从以上过程可看到，Excel是一款集表格处理、数据管理、统计制图、统计分析于一体且实用性强操作简单方便的办公软件。借助Excel，几乎可以完成所有统计数据分析与处理，我们可以根据需要选择不同的方法。

参考文献：

[1]盛骤等.概率论与数理统计[M].北京，高等教育出版社.2001年12月第三版.294-313

[2]范秀荣等.统计学原理[M].北京，高等教育出版社.2010年8月第一版.197-203

[3]王剑武等.统计学[M].长沙，湖南师范大学出版社.2014年1月第一版.192-198

[4]黄应绘等.统计学实验[M].成都，西南财经大学出版社.2009年7月第二版.111-121

作者简介：

黄基廷（1964-），男，广西天等县人，副教授，主要从事应用数学研究.