混凝土二维随机骨料模型的改进
陈浩 宓永宁 岳川 毕建成


摘要:在越来越高的模拟精度要求下,针对随机骨料结构中粒径分布控制和黏结界面层生成环节中存在的问题,基于Walraven公式推导出改进的骨料分布函数,就椭圆形骨料和任意凸多边形骨料提出生成均匀界面层的方法,有效提高随机骨料模型的仿真程度,为混凝土细观数值模拟研究提供更优质、更合理的骨料模型。
关键词:混凝土,随机骨料模型,粒径分布,黏结界面层,算法改进
中图分类号:TU528 文献标识码:A 文章编号:1674-1161(2015)03-0049-04
为研究混凝土细观结构与其力学性能的关系,根据骨料在混凝土结构空间内随机分布的特性,提出混凝土随机骨料模型。随机骨料模型理论认为,混凝土是由粗骨料、水泥砂浆和二者间的粘结界面组成的三相复合材料,借助蒙特卡罗方法,在投放空间内随机确定骨料的形状、位置和尺寸,产生的随机骨料结构。近年来,研究人员在二维随机骨料生成算法方面做了大量研究,取得了丰富的成果,从不同角度解决了随机确定骨料形状和位置的问题,其中高政国、孙立国、严兆等先后提出了不同的二维随机骨料生成算法。随机骨料结构中骨料粒径分布通常借助Walraven公式来确定,其方法有代表粒径法和反函数法,但前者是一种简化方法,对粒径分布的描述较为粗略;后者将随机概率值Pi直接代入Walraven公式求取粒径值Di。然而,事实上Walraven公式中的概率值是面积百分率,与颗粒数目百分率是不等同的,由此生成的骨料结构中大粒径颗粒严重偏多。
针对这两种方法存在的缺陷,以Walraven公式为基础推导混凝土结构横断面骨料数目累积分布函数PN(D),并用统计学方法对该骨料分布函数的合理性进行论证,然后通过模型对比证明该方法能够有效提高随机骨料模型的仿真程度。
在混凝土随机骨料结构中,黏结界面层可视为粗骨料与硬化水泥砂浆之间的一个过渡薄层,相当于在原有骨料颗粒表面均匀地向外延伸一个厚度。许多研究表明,黏结界面层的力学特性在很大程度上决定混凝土的宏观强度,因此在进行混凝土结构的细观数值模拟时,生成的界面层是否合理将直接影响模拟结果的准确性。在实际建模中,通常的做法是通过投放比要求颗粒粒径稍大的颗粒,然后按比例缩小,完成界面层的生成。但这种处理方法仅适合圆形骨料,椭圆形和任意多边形骨料很难保证界面层厚度的均匀性。在网格尺寸以微米计量的有限元分析中,这种非均匀性导致的误差对结果的影响是不容忽略的。为此,针对椭圆形骨料和任意凸多边形骨料的几何形状特征,提出各自的界面层生成算法,以期达到提升模型精度的目的。
1 骨料粒径分布的随机性改进
1.1 混凝土三维骨料级配的平面转化
20世纪80年代,Walraven.J.C将混凝土三维试件中的骨料颗粒简化为以骨料形心为圆心、以骨料粒径为直径的球体,根据Fuller级配曲线和骨料在试件空间等概率分布的几何学概念,推导出三维骨料级配的平面转化公式,即Walraven公式:
式中:PC(D)为截面上任意一点位于粒径小于D的骨料颗粒上的概率,即截面上直径小于D的截面圆面积占截面面积的百分比;PK为骨料(粗骨料和细骨料)体积与混凝土总体积的百分比;Dmax为骨料最大粒径。
1.2 骨料粒径分布的随机性改进
近年来,随着混凝土数值模拟研究的逐渐深入,模拟的精度也不断提升,由代表粒径法生成的骨料形状多样、骨料粒径特定的随机骨料结构已经不能满足应用要求。反函数则由于混淆了两个概率值,因此确定的骨料结构严重偏离实际,也存在严重不足。为实现随机骨料结构中骨料尺寸的随机确定,提高建模水平,亟需找出一种可实现骨料粒径随机生成的数学控制方法。
此处需要加以说明的是,在数理上面积百分率与数目百分率是完全不同的概念,例如单个大粒径骨料在粒径-面积率和粒径-数目百分率累积曲线上的Y轴增量明显不一致,因此一些研究直接将随机概率值代入Walraven公式求解粒径值的做法是不合理的。
1.3 统计验证
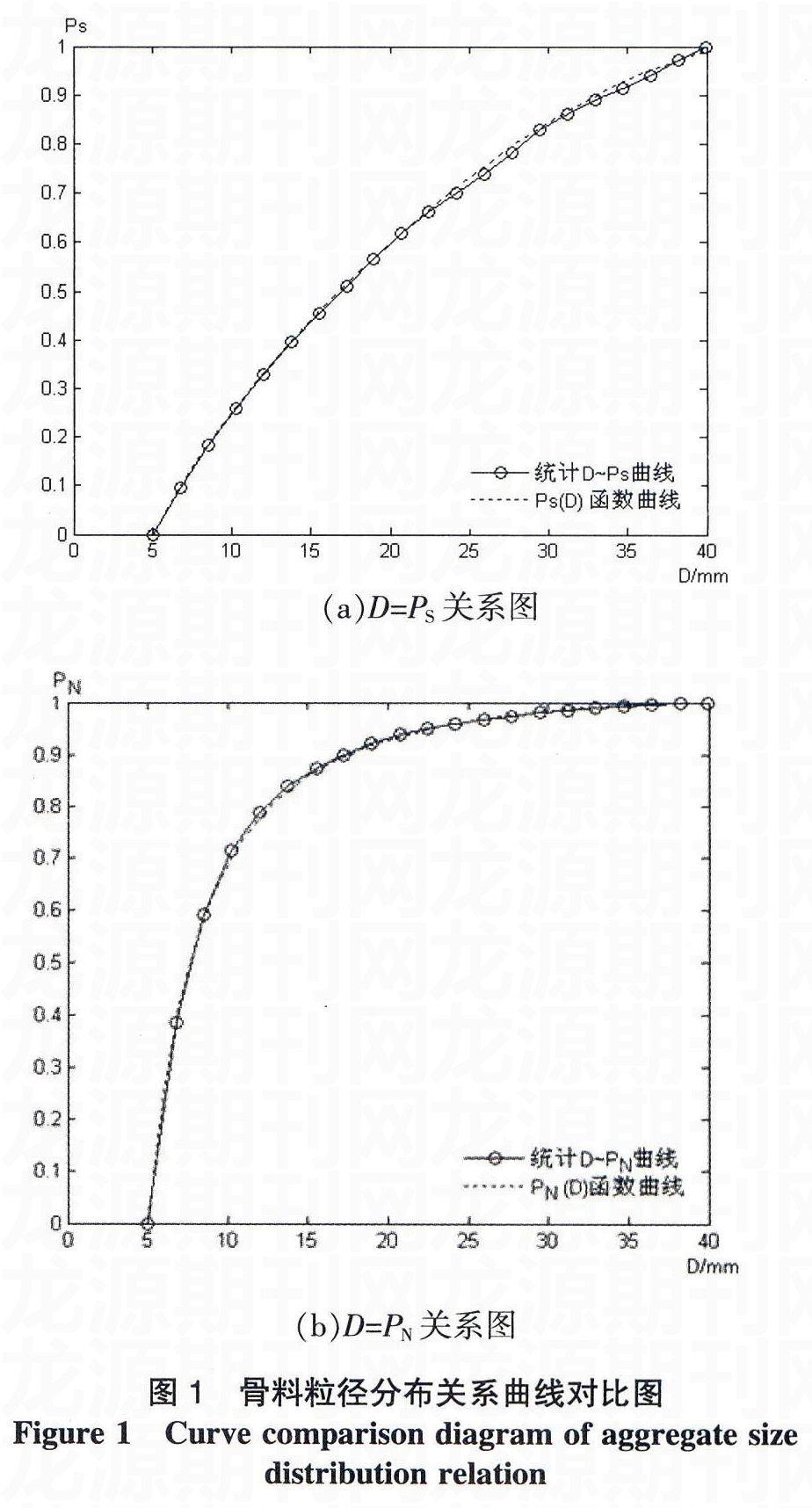
生成Fuller级配曲线的三维混凝土球形随机骨料模型,对模型各截面上不同直径截面圆数目和累积面积率进行数理统计,得出统计D-PS和D-PN关系曲线,同时绘制骨料粒径分布函数PS(D)和PN(D)的函数曲线,如图1所示。
图1(a)中,PS(D)函数曲线和统计D-PS曲线极为吻合,这说明PS(D)能够准确描述骨料累积面积率和粒径的函数关系;图1(b)中,PN(D)函数曲线和统计D-PN曲线非常一致,这表明PN(D)对骨料累积数目和粒径函数关系的描述符合实际。由此可见,推导的骨料分布函数能准确描述混凝土实体结构横断面的骨料粒径分布规律,具备数理上的合理性。
1.4 模型对比
分别运用两种常用方法和本文提供的改进方法建立随机骨料模型,生成的骨料结构分布如图2所示,其中图2(a)为二级配混凝土,骨料粒径代表值为12.5,30.0 mm。从三维模型中随机截取一个截面作为实体对照,其骨料结构如图2(d)所示。
图2(c)的骨料粒径分布与图2(d)非常相似,骨料含量也很接近。相对而言,图2(a)的颗粒数目较少且级配较差,图2(b)大粒径颗粒过多、骨料数目最少且级配也最差。上述对比显示,改进方法生成的骨料结构对混凝土骨料级配及含量的数值化表现更为准确合理。
2 界面层厚度的均匀性改进
在综合考虑运算规模及计算效率的情况下,混凝土细观结构模型中的界面层厚度一般会偏大于实际界面层厚度,通常取0.05~0.10倍粒径。目前,大多通过按比例放大粗骨料来获得一个厚度近似均匀的界面层,但实际上椭圆和任意凸多边形骨料(尤其是扁度偏大的椭圆和各边长相差较大的凸多边形)生成的界面层在厚度上存在明显差异。就椭圆形骨料而言,其差异最大为半长轴a与半短轴b差值的0.05~0.10倍(当a=40,b=20时,为1~2 mm)。在较高的模拟精度要求下,这些差异对模拟效果的影响难以忽略。
2.1 椭圆形骨料均匀界面层的生成
以式(14)为参数方程,便可生成一个厚度均匀一致的界面层,如图4(b)所示。图4(a)是通用方法所生成的椭圆形骨料界面层。
从图4(a)可以明显看出,通用方法获得的界面层在厚度上很不一致,椭圆长轴两端界面层最厚,而短轴两端则最薄;而图4(b)所示的骨料界面层厚度完全均匀一致。
2.2 任意凸多边形均匀界面层的生成
在工程实际中,配置混凝土时最常用的粗骨料是碎石。因而在建立混凝土随机骨料模型时,一般会将骨料形状设定为任意凸多边形。图5(a)是采用放大骨料的方法生成的单个凸多边形骨料结构,骨料表面不同部位的界面层厚度差异显著。
均匀界面层生成思路是:将多边形各边的端点延垂线向外侧等距平移,再用半径等于界面层厚度的圆弧连接各相邻线段的端点,将平移后的孤立线段封闭成一个等厚度包裹在凸多边形表面的圆角多边形,如图5(b)所示。和图5(a)相比,图5(b)中黏结在骨料表面的界面层厚度完全均匀一致。
3 结论
受网格质量以及计算规模的限制,混凝土细观数值模拟的研究重点仍限于二维层面。合理构建三维级配和二维骨料粒径分布的转化关系,是二维随机骨料生成方法中的核心问题。
改进二维随机骨料生成方法弥补了传统方法的缺陷,真正实现了骨料粒径的随机生成,生成的随机骨料结构中,骨料粒径分布和含量更符合混凝土结构横断上骨料的分布实况。此外,改进的均匀界面层的生成算法,提高了模型数理上的精确性。
这两方面的改进可显著提高随机骨料模型的仿真程度,使混凝土细观数值分析在更高精度下进行,为揭示混凝土细观结构和宏观力学性能的关系提供模型基础。
参考文献
[1] 高政国,刘光廷.二维混凝土随机骨料模型研究.清华大学学报(自然科学版),2003,43(5):710-714.
[2] 孙立国,杜成斌,戴春霞.大体积混凝土随机骨料数值模拟[J].河海大学学报(自然科学版),2005,33(3):291-295.
[3] 严兆,汪卫明.全级配混凝土随机骨料二维模型生成的块体切割方法[J].武汉大学学报(工学版),2013,46(4):484-488.
[4] WALRAVEN J C, REINHARDT H W. Theory and experiments on the mechanical behavior of cracks in plain and reinforced concrete subjected to Abstract: With the requirement of simulation accuracy increasing, the method of generating uniform interface layer by managing ellipse aggregate and arbitrary polygon aggregate based on improved aggregate distribution function derived by Walraven formula is presented. It solves the problems existing in the control of particle size distribution in random aggregate structure and the links of bonding interface layer generating, and effectively improved the simulation level of random aggregate mold, provided a aggregate mold of more logical and higher quality for the research of mesoscopic numerical simulation of concrete.
Key words: concrete; random aggregate mold; particle size distribution; bonding interface layer; algorithm improving

