城市流动警务平台的设置与调度模型研究

张 新 赵书银 武小云

（河北建筑工程学院，河北 张家口075000）

0 引 言

在社会主义市场经济新体制和城镇化建设不断加快的新形势下，城市加速扩张，人口迅速增长，道路交通问题日益严重，恶性犯罪事件也呈上升趋势，社会治安动态化的特点越来越明显，治安管理的任务也越来越繁重，但警务资源是有限的，一旦发生突发事件，根据实际情况合理调度警务资源就显得尤为重要.因此科学确定城市流动警务平台的数量和具体位置，合理调度警力资源，具有极大的现实意义和实用价值.

1 问题分析与模型的建立

1.1 问题及模型假设

本文根据笔者所在市某中心区域的交通网络，探讨城市流动警务平台的位置及分配各城市流动警务平台的管辖范围.具体探讨以下几个问题：

（1）已知该区域的交通网络图和相邻两个交通路口之间的距离，确定该区域中任何两个交通路口之间的最短距离.

（2）在警力有限的情况下，根据现有城市流动警务平台的数量，设置城市流动警务平台的位置及分配各自的管辖范围.这里假设出警的时间只和两个路口之间的距离有关，在给定城市流动警务平台个数的前提下，使得出警时间最长的路口所用的时间最少.

（3）为了实现警务人员能够以最快的时间到达案发现场，应该确保每一个城市流动警务平台所管辖的路口节点个数尽可能均衡，从而需要对问题进一步优化.

1.2 符号说明

C：所考虑区域路口节点的集合，本文测量了39个路口节点的数据，即

C＝ ｛1，2，…，39｝

ci：区域的第i个路口节点，在集合C中；

P：城市流动警务平台节点的集合，集合有个城市流动警务平台，即

P＝｛1，2，…，9｝

D＝（dij）39×39：各路口节点之间的距离矩阵.其中dij表示第i个路口节点到第j个路口节点的距离，因为问题中所有涉及到的街道都是双向行驶的，所以D是对称矩阵.

2 计算各路口之间的距离矩阵

根据地图测出相邻两个交通路口之间的距离，使用Floyd算法可以得到区域中任意两个交通路口节点之间的距离，从而得到距离矩阵D.

3 城市流动警务平台的设置和调度

为了确定城市流动警务平台的位置和各自管辖的路口，引入一个0－1变量：

由于并不是每个路口都有城市流动警务平台，所以再引入一个0－1变量：

这样，变量xij和bj满足：

（1）只有当第j个路口被设置城市流动警务平台，也就是bj＝1时才可能有xij＝1.

（3）城市流动警务平台总个数为9个，即

（4）城市流动警务平台所在的路口受该平台管辖，即xjj＝bj，因为当bj＝0时，节点处没有城市流动警务平台，故相应的路口不受该节点管辖，所以这个约束是总是成立的.

目标函数考虑所有城市流动警务平台到被管辖的路口节点的距离的最大值要尽可能小，也就是任何一个路口节点发生案件后，能确保警务人员用尽可能少的时间到达案发现场.所以目标函数是求解下式的最小值.

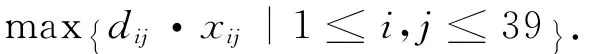
所以问题就转化成如下的0－1整数规划模型：

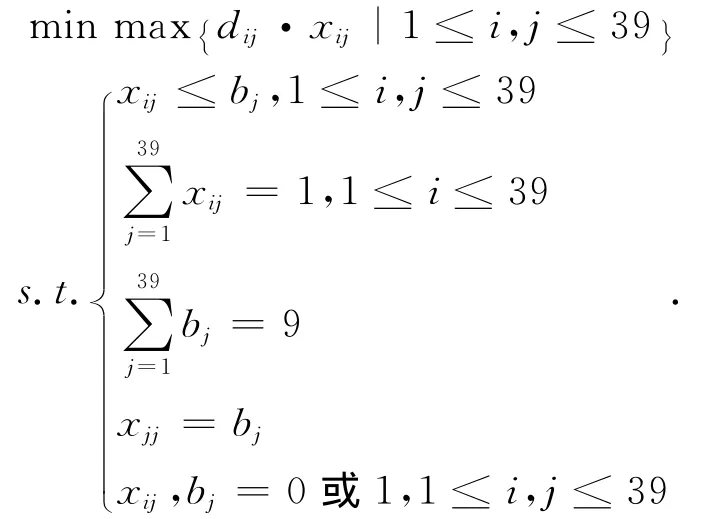
使用LINGO求解，得到最优解为2.516km，为在26路口节点设置的城市流动警务平台到33路口节点的距离.具体分配方案为：

城市流动警务平台所在节点 管辖路口的节点1 1 2 2 3 3 10 8 8 13 5 6 7 13 20 14 4 9 11 12 14 15 16 17 18 19 25 25 34 26 21 22 23 24 26 28 29 30 31 32 33 35 36 37 38 27 2739

可以看出，这种方法求出的结果，其缺点也是显而易见的，就是会出现“扎堆”现象，即某个城市流动警务平台需要管辖的路口节点太多，导致管辖范围分配不合理.，像上述算法求得在26号路口设置的城市流动警务平台的管辖路口节点的个数竟然是15个，显然偏大.假设每个路口节点的发案率相同，要求尽可能使得每个城市流动警务平台管理的路口节点个数均衡.在确保最大距离不超过2.516km的前提下，使用得到的城市流动警务平台节点，可以重新分配每个城市流动警务平台的管辖范围，实现均衡管辖路口节点的目的.

为此，目标函数为每个城市流动警务平台管辖路口节点个数的最大值尽可能小，即

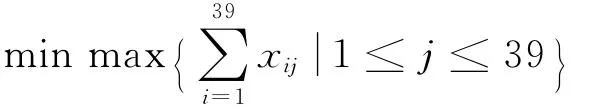
约束条件为：

（1）每个路口节点到城市流动警务平台的距离不能超过2.561km，即dij·xij≤2.561.

（2）当节点j未设置城市流动警务平台时，xij＝0.

算法如下（这里bj是已知的）：

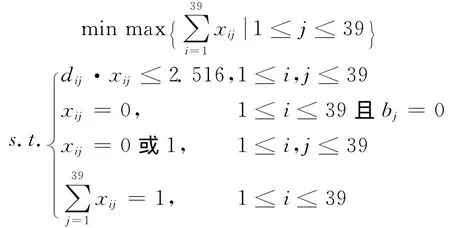
使用LINGO计算得到每个城市流动警务平台管辖路口节点个数的最大值可以取为8，但是相应的分配方案仍不够合理，现在把作为约束条件，将目标函数调整为的最小值，也就是所有路口到相应的城市流动警务平台的距离之和的最小值，得到如下的分配结果：

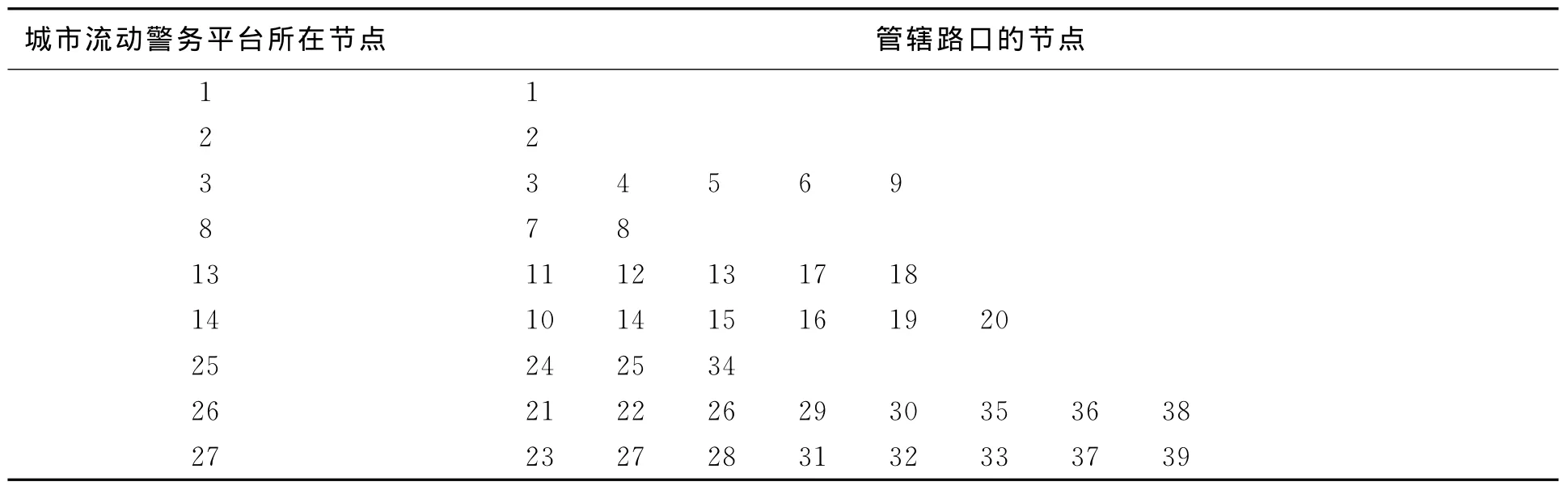
城市流动警务平台所在节点 管辖路口的节点39 1 1 2 2 3 3 4 5 6 9 8 7 8 13 11 12 13 17 18 14 10 14 15 16 19 20 25 24 25 34 26 21 22 26 29 30 35 36 38 27 23 27 28 31 32 33 37

目标函数最小值为37.772km，所得的结果是全局最优解，在实际问题中应用也是合理的.

4 结 论

本文利用图论及运筹学的相关知识，根据某市交通网络实际情况，建立了以出警时间尽可能小、工作量均衡为目标的数学模型，并对模型的合理性进行了评价及优化，最后得出了较合理的结果.但本文没有考虑忙时交通拥堵对到达案发现场时间的影响，这个问题可以用加权矩阵实现，而且本文讨论的车道都是双向车道，但是因为即使是单向车道，Floyd算法对有向图仍适用，所以本文算法适用于道路中存在单向车道的情况.

［1］辛驰.关于交巡警服务平台设置与调度的数学问题［J］.广东科技，2012，21（17）：201～202

［2］张成堂.城市交巡警平台的设置与调度优化模型［J］.重庆理工大学学报：自然科学版，2012，26（11）：63～68

［3］杨争.基于区域最短路径算法的警力调配系统［J］.重庆理工大学学报：自然科学版，2010，24（6）：44～47，60

［4］胡运权.运筹学教程［M］.北京：清华大学出版社