试析高中学生数学运算能力的组成要素
☉福建省尤溪第一中学 肖兰珠
试析高中学生数学运算能力的组成要素
☉福建省尤溪第一中学 肖兰珠
运算能力、逻辑思维能力和空间想象能力被喻为数学三大基本能力,而笔者认为在三大基本能力中犹以运算能力为基础,这里的运算能力不仅仅是计算能力,它有着丰富的内涵,包括对基本概念、基本公式灵活运用的能力;还包括综合与分析条件,寻求简单路径的能力.可以说运算能力是学生数学成绩的决定性要素之一.因此,有必要从数学运算能力的组成成分上对其解读,以更好地培养学生的运算能力.笔者认为数学的运算能力主要包括如下几个方面:首先,依据对象的特点,选择适当数学模型的能力;其次,依据对象的特点,选择恰当运算方法的能力;第三,依据对象的特点,挖掘隐含信息的能力;第四,依据对象的特点,运用恰当数学思想的能力;第五,依据对象的特点,选择恰当运算路径的能力.
一、依据对象的特点,选择适当数学模型的能力
数学模型在本质上是内在数学各要素的结构关系,外在表现上往往被抽象成建立在数学符号基础上的等式、不等式、图像、图表等内容.简单地讲,选择适当的数学模型的能力就是将问题归入哪类知识点的判断能力,从这一层面讲,提升学生运算能力的第一要求即提升学生的数学模型选择能力.数学题目往往存在着知识交汇的情况,因此每道题目通常会存在至少一种数学模型,同样的题目,因为选择模型的不同,往往会呈现出繁简程度截然不同的现象.
分析1:遇到带有绝对值的最小值,学生们易选择的数学模型是函数,即进一步选择分段函数这一数学模型.
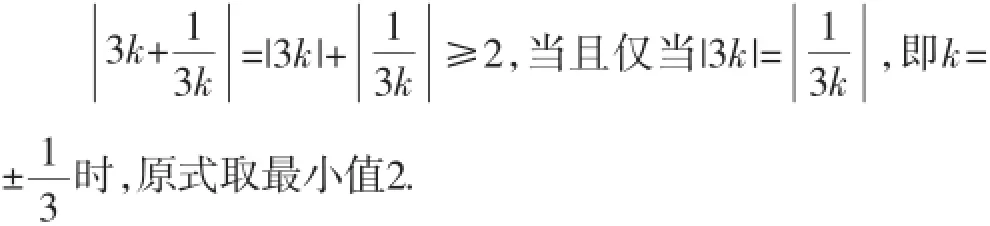
反思:虽然两种思路最终均得到了正确结果,但对比两种思路可以发现:第一种方法中明显运算的速度被拖了下来,而第二种方法在运算上则呈现出截然不同的运算景象.造成这种运算差异的根本在于选择的数学模型不同,第二个数学模型是基于学生高度的抽象能力基础上的.
二、依据对象的特点,选择恰当运算方法的能力
运算方法,简称算法,即在理解数学问题情境的基础上,通过对数学数据的分析,找出解决问题的具体步骤,这一组连续的操作步骤即算法.同一道题目,往往因为选择的算法不同,而影响到解题过程的复杂程度和运算量的大小.运算能力较强的学生,往往能够因“问”制宜,从众多的算法中选择与问题情境适合的算法,从而简化问题解决过程,降低运算量,从而确保运算快、准、稳.

分析1:判定函数奇偶性有固定的步骤:首先,分析定义域是否关于原点对称;第二,验证f(-x)与f(x)的关系;第三,判定奇偶性.
易证函数的定义域为R,关于原点对称.

分析2:f(-x)=-f(x)等价于f(-x)+f(x)=0,在证明函数为奇函数时往往不用第一个等式,而选择第二个式子,两者区别在于运算的路径选择不同.
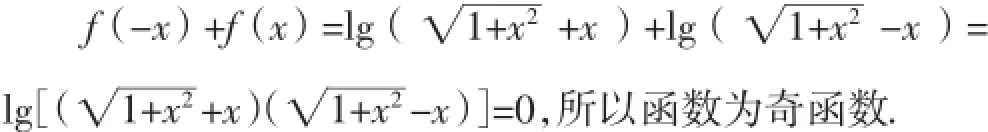
反思:受前摄抑制的影响,学生一般在心理上更认可的是分母有理化,而非分子有理化,并且分子有理化的过程也非常复杂,因此,学生在运用第一种方法时,计算往往比较“痛苦”,相比较而言,后一种方法仅仅运用了对数的加法公式和平方差公式,繁简对比,立竿见影.因此在数学运算时不能机械地套用公式,而应根据具体情境选择适当的运算方法.
三、依据对象的特点,挖掘隐含信息的能力
很多试题为了考查学生能否灵活运用所学内容,往往在题设中并不直接给出所需要的条件,而是将其隐晦表达在已有的条件中.另有研究表明,学生的运算速度及其准确性,受其挖掘隐含信息的能力的影响.因此,依据对象的特点,在已知条件的基础上挖掘题目的隐含信息是增强学生运算能力的重要途径.
例3已知{bn}是等比数列,bn>0,若b2b4+2b3b5+b4b6= 36,那么b3+b5的值为?
分析1:对于与等比数列的项有关的问题,回归基本量首项和公比是一种常见的思路,通过基本量的计算求解每一项的值,或者将待求的表达式整体用基本量来表示,从而达到求解的目的.
设首项为b1,公比b3+b5=6.
分析2:再次观察题设可以发现:题设中暗含着等比数列的一种性质,即等比中项,并且条件中所给出的等式利用等比中项替换后恰好是待求表达式的完全平方式,挖掘到这一隐含条件有助于提升学生的运算效率.
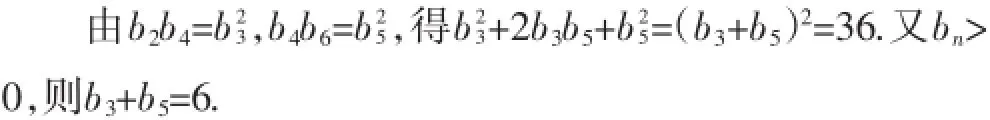
反思:类似这样含有隐含信息,需要学生去挖掘的问题还有很多,比较两种处理方式可以发现:后一种的运算明显比前一种情况简单.因此,对于提升学生的运算能力而言,提升学生挖掘隐含信息的能力是重要的一环.
四、依据对象的特点,运用恰当数学思想的能力
众所周知,高中阶段主要会接触到分类讨论、函数与方程、数形结合、转化与化归等七类基本数学思想.笔者认为对数学思想方法的运用应当是数学运算能力的一个组成部分.如下以转化与化归思想为例,说明数学思想在提升运算方面的作用.

分析:很多学生的思维是将其两侧平方,显然这是不可取之法;亦有学生会想到利用两根式的单调性来求解,但发现两者的单调性并不一致,这样就导致了学生会陷入思维的困境,难以突破.而利用转化的数学思化成直线y=x上的点到(2,0)和(1,2)的距离之和的最小值.可以发现(2,0)和(1,2)分布在直线的两侧,因此,原
反思:很多时候在问题情境中,直接运算往往难以直接进行,这时就需要借助数学思想的力量.例如转化与化归思想,例4中将代数表达式转化成几何意义动点到两定点的距离之和;再比如数形结合思想,就是函数问题中将用的数学思想.总之,数学思想的正确运用往往能够简化问题的计算,提升学生的运算能力.
五、依据对象的特点,选择恰当运算路径的能力
运算路径的选择直接决定着运算步骤的数量,直接决定着运算过程的繁简程度,因此,依照问题的具体特点,选择恰当运算路径的能力应当被视为衡量学生运算能力的一项重要指标.如下以一道解析几何题为例,展示由于运算路径不同而造成运算的差异.
例5焦点在y轴上的椭圆,过其上焦点F1作y轴的垂线交椭圆于M点,若△F1F2M为等腰直角三角形,求椭圆的离心率.

分析1:对于有关离心率的问题,通常的思路是构建一个关于a、c的齐次等式,将等式转化成关于e的方程求解.

分析2:反思上述过程,选择的路径是构建一个齐二次等式,而观察图形可以选择一个更简单的路径,利用椭圆的定义构建齐一次等式.

反思:比较两种方法,方法1选择的路径为解二次方程,方法2选择的是解一次方程,两者的运算繁简高下立见.管中窥豹,可见一斑,由上述这一简单的例题就可以反馈出运算路径的选择对运算速度提升的重要性.
总而言之,学生的数学运算能力是影响学生成绩的主要因素,而数学模型的建构能力、运算方法的选择能力、隐含信息的挖掘能力、数学思想的运用能力则是数学运算能力的重要组成,因此,提升数学运算能力应当从上述几个方面着手.
1.黄小宁.造成学生运算能力差的心理因素[J].天水师范学院学报,2000(S1).
2.詹润翠.高中学生数学运算能力及其培养研究[D].呼和浩特:内蒙古师范大学,2011.
3.黄伟秀.在数学教学中应重视运算能力的教育[J].中学数学教学,2007(2).
4.简洪权.高中数学运算能力的组成及培养策略[J].中学数学教学参考,2000(Z1).
5.曹凤山.从一道高考题看高考对运算求解能力的考查[J].中学数学(上),2010(10).A

