在汲取知识的过程中发展学生的智慧——从“等差数列”的复习课设计谈起

☉江苏省白蒲高级中学 缪德军

教学参谋

在汲取知识的过程中发展学生的智慧
——从“等差数列”的复习课设计谈起

☉江苏省白蒲高级中学 缪德军

复习课是数学教学中的一种常见课型.有人说，平时的教学是栽活一棵棵树，复习课就是为它们灌溉，使它们更茁壮地成长为一片林.因此，复习课在厘清有关基础知识、基本方法，使它们结成块、组成网的基础上，还要搞清相关知识发展的来龙去脉、思维的发生与发展，让学生从具体操作基础上的理性认识过渡到宏观指导下的整体认知，进而构建研究一类相关对象的思路和方法，也即学生的一种认知智慧.

实际复习课中，有的课堂收集大量习题，让学生在题海里苦战；有的“爆炒冷饭”，让学生机械重复地训练；有的采用“练习→讲评→再练习→再讲评”的教学方式，把学生会做每一道复习题作为教学目标.这样教师累得不行，学生苦不堪言，而收效甚微，最为关键的是，这样的课堂给学生留下的更多的是做了很多题，而不能留下思考研究一类问题的策略和方法，也即思考解决问题的智慧.

笔者最近执教南通市公开课“等差数列”，尝试在复习设计上寻求突破，以求得让学生在汲取知识的过程中更加发展学生的智慧，收到了良好的复习效果.

一、知识梳理，启发思维

案例1：完成下列4题，并思考每道题所用到的有关知识和方法.

（1）在等差数列｛an｝中，前n项和为Sn，若a6=S3=12，则an=______.

（2）在等差数列｛an｝中，已知a1+a3+a5=18，an-4+an-2+an= 108，Sn=420，则n=______.

（3）在等差数列｛an｝中，前n项和为Sn，已知S4=2，S8=6，则S12=______.

（4）已知两个等差数列｛an｝和｛bn｝的前n项和分别为

设计意图：通过一组基本题的练习，帮助学生回顾等差数列的基本概念、公式与性质，让学生在知识运用中再次理解有关公式、性质和方法，从而在基础知识和基本方法的理解中建构自己的知识框架，进而使知识系统化、结构化，以加深对知识的理解及知识之间内在联系的把握，便于相关知识在解决数学问题时能够被灵活有效地调用.

教学过程：组织学生先独立完成各小题；然后小组（每6人一组）合作学习，讨论交流每道题所用到的知识及解决方法；一个小组代表在班级展示，其他组补充、完善；最后师生共同总结，形成基本认知框架.

小组3补充：对于第3题，也可以利用结论“若｛an｝成等差数数列”转化为新数列来解决.

小组4展示：对于第4题，利用性质：若两个等差数列｛an｝和｛bn｝的前n项和分别为An、Bn，

小组6解答：根据比例关系，设An=k（2n+1），Bn=k（n+ 3），再求得an、bn即可.

小组4质疑：这样求得的an=2k、bn=k不

（沉默，各小组不自觉地讨论了起来）

小组7释疑：回到等差数列的求和公式，应该看到，An、Bn是关于n的二次式，设An=k（2n2+n），Bn=k（n2+3n），再利用an=Sn-Sn-1（n≥2）化和为项就可以了！

（鼓掌）

学生连续的、深刻的、有效的思维在此显现无疑.最后，教师跟学生一起对刚才的过程进行总结、归纳、梳理.在此，既梳理了知识，又体现了方法，更揭示了思维.

设计反思：传统教学中，教师往往直接把一些概念、公式、结论、定理告诉学生，让学生记住，然后进行大量训练，学生通过大量训练会产生一种即时的效果，但随着时间的推移，这种模式容易被固式，一旦遇上新的问题，学生也就束手无策了.

在这里，给学生几个简单的问题，由学生独立或合作完成，问题解决的过程中，学生自然、不自觉地进行着有关基本知识与方法的回忆与梳理，再次强化理解了这些知识的来龙去脉和内在蕴含的结构联系，经过这样的梳理所形成的基本知识结构就不单单是知识记忆层面的，更有思维理解层面的，它是一个立体的、鲜活的知识架构，在今后的问题解决中，学生大脑中的有关信息更容易被具体情境快速激活.

二、典例剖析，凝练思维

案例2：设等差数列｛an｝的前n项和为Sn，已知S4≥10，S5≤15，求a4的最大值.

设计意图：通过典型例题的研究与解决，寻求解决一类问题的方法与策略，凝练学生解决常见问题的常规思维，为进一步研究相关问题打下坚实的基础.

教学片断：学生先独立完成，然后小组（每6人一组）合作学习，讨论交流不同解法；一个小组代表在班级展示，其他组补充、完善；最后师生共同总结、归纳.

解法1：利用线性规划知识.

在直角坐标系a1Od中，作出不等式组所表示的可行域（如图），当斜率过点（1，1）时，a4取得最大值4．

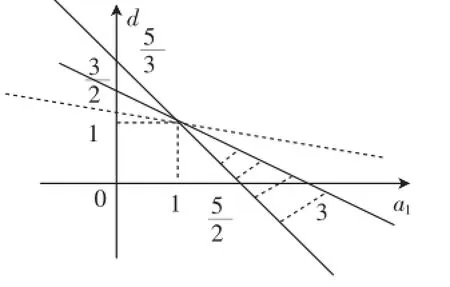
师：讲得很好，但有一点需要修正，二元函数的最值问题常用线性规划知识或待定系数法来处理是不错，但更为重要的方法是利用基本不等式、消元法和数形结合，而利用线性规划知识仅只是数形结合中的一类情况.哪一位同学来点评一下三种解法？

生1：解法1、2实际上是一样的，都是用基本量a1、d来表示条件和结论，利用线性规划知识或待定系数法来处理；第三种解法联系性质，比前两种解法简洁.

师：点评准确，仍旧是基本量法和性质的运用，转化后就是一个二元函数的最值问题，后面的处理值得注意.从以上解法中可以看到数列的公差d的取值范围吗？

生2：d≤1，从解法1和解法3中容易看出.

设计反思：复习课是在学生已有相关知识基础上的教学.因此，在复习课上，应留给学生更多的时间与空间，组织学生的学习活动，引导学生进行相关问题的自主与合作学习，从而在自主学习与合作探究中主动建构.

处理本题的方法很多，但不论是哪种方法都要让学生明白解决一个等差数列问题，要考虑回到等差数列的定义，从等差数列最基本的量a1、d出发，再去联系其他，这是学生最容易接受也是最容易做到的.因此，在复习课上，应坚持让所有的问题都从基本概念、公式、性质的理解和基本题的熟练掌握开始，让目标的达成由易到难，循序渐进.

三、设疑引问，创新思维

案例3：设等差数列｛an｝的前n项和为Sn，已知S4≥10，S5≤15，求ak（k≥4）的最大值.

设计意图：对例题进行深入的研究，以期从复习等差数列的定义扩展到所有与等差数列的通项公式和前n项和公式相关的问题，甚至扩展到等差数列的有关性质，加深学生对等差数列的通项公式、求和公式以及相关基本性质的认识和理解，以起到一种宏观建构的作用.

教学片断：师：d≤1结合a4≤4，能看到什么？

生3：a5≤5.

生4：进一步可以得到a6≤6，a7≤7，…，ak≤k（k≥4）.

（全体同学一片欣喜）

师：再联系条件S5≤15，我们还能想到什么？

生5：可以看到S6=S5+a6≤21，S7≤28，…，进一步可求得Sn的最大值.

（全体同学鼓掌）

到此，学生在解决问题的过程中，不断认识问题的本质，并从本质的理解与思考中提出了新的问题，激发了学生的思维活力.

师：对于新问题“设等差数列｛an｝的前n项和为Sn，已知S4≥10，S5≤15，求S6的最大值”，还需要回到求a4的最大值的思路上吗？

生6的自语：把S4、S5、S6都用基本量a1、d表示出来，然后用线性规划知识或待定系数法来求，但好像比较繁．

生7：我有一个简单的方法.设Sn=An2+Bn，把S4、S5、S6再用线性规划知识或待定系数法求S6.

师：你为何想到这么做？

生7：这里条件和结论中只有Sn.

师：太好了！等差数列问题中，既有Sn又有an时，用a1与d统一关系较为合理；若仅涉及Sn时，设Sn=An2+Bn统一关系运算较为简捷.

（留时片刻，让学生体会并加以理解）

生8突然发言：老师，我还有一个方法.这个题还可以用刚才的性质来解，“若Sn是等差数列的前n项和，则｛an｝的前n项和，S4≥10，S5≤15，求S6的最大值”就转化为用｛bn｝的首项b1和公差d来表示，再用线性规划知识或待定系数法可求得b6，再求S6.

生9：还可以更简单，令bn=dn+k，和刚才Sn时一样，bn也可以简化！

师：太棒了！学生的思维被激活了！

牛刀小试：（2004年高考江苏第20题变式）设无穷等差数列｛an｝的前n项和为Sn，求所有无穷等差数列｛an｝，使得对一切正整数k都有Sk2=成立．

设计反思：一个看似简单的问题，却包含着如此丰富的内容与思想，在问题的引导、学生的独立思考与合作探究中进行着深入的剖析、挖掘、生成、变式与拓展，不仅加深了学生对原有问题的理解，更重要的是在解法的探究、问题的变式拓展的过程中，学生通过类比或归纳的思想提出新问题、发现新结论继而解决新问题的能力得到了真正的培养.如此围绕框架性主题的一题探究，可有效摒弃“题海战术”，从而提高典例教学的有效性.

复习课要训练学生模式化的解题思维，让学生熟练掌握解决常规问题的通性、通法，但思维不能固化.在此，复习要设计及时的设疑、追问，能让学生的思维走向灵活、走向深入，进而在深入思考中发现新的问题，并提出问题，提出问题永远比解决问题来得更重要.如此，学生的思维将更加深刻、更加多向，解决问题的思维必会得到创新.更重要的是学生在问题解决的过程中学会了一类对象的思考方法，而这正是发展了学生的学习智慧.A