一种适用于海上风机监测数据实时处理的方法研究

周建华，吕鹏远，王 春

（1.中国水利水电科学研究院 北京中水科工程总公司，北京 100048；2.响水长江风力发电有限公司，湖北 盐城 224600）

一种适用于海上风机监测数据实时处理的方法研究

周建华1，吕鹏远2，王 春1

（1.中国水利水电科学研究院 北京中水科工程总公司，北京 100048；2.响水长江风力发电有限公司，湖北 盐城 224600）

海上风机监测异常数据实时处理，对于风机结构体系功能与安全状态的分析评价，具有十分重要的意义。但现阶段对于异常数据实时处理方法的研究还有待完善。本文结合风机实时监测数据特点，采用具有自动调整参数功能的AR（n）模型预测算法进行异常数据实时处理，对处理机制进行了分析。应用该方法对某海上风机实时采集风速及多种传感器监测数据进行了处理，讨论了该方法的精度及处理效率，验证了该方法对于处理风机异常监测数据的有效性和适用性。

异常数据；实时处理；处理机制；AR（n）自动调参预测模型

1 研究背景

近年来，对海上MW级风机安全运行状况进行实时监测成为研究热点。现有海上监测技术主要针对海上风机所受荷载及相应的响应进行监测，原始数据经过数据存储、分析及处理，得到基础的安全运行状况和维修决策等结论。由于基础结构损坏、监测对象固有变化异常、测量仪器故障、数据传输错误或者噪音信号掺杂等原因，常常引发传感器监测数据的异常。如果不能实时有效地对监测数据流中的异常数据进行处理，异常信息不能有效辨识，缺失信息不能有效修复，会给后续数据处理与分析带来很大的误差，低精度和异常的监测数据会严重影响对基础结构体系功能与特性的分析评价，威胁风机基础安全运行。

通过对于海上风机监测数据的分析研究及相关研究成果的归纳总结，得到海上风机监测数据的以下特点［1-3］：无固定的分布模型，随季节变化而变化，随时间变化非线性强，数据具有较高不确定性，无法提供大量可信的训练数据，监测数据流每天波动范围相对小，变化趋势相近；监测数据种类多，格式复杂、信息量大，每天数据量甚至能达到十几GB。

针对风机实时监测数据特点，国内学者已经研究了很多处理办法，如小波分析、数据挖掘和数据流理论等，然而，常用方法包含大量参数、算法比较复杂，占用较大的存储空间、计算效率较低，且具有代表性的样本数据的选取也是亟需解决的问题［4］，因此主要适用于处理离线异常数据，对于海量实时异常数据处理还存在一定的困难。对于风机实时异常数据，处理方法既要充分体现数据分布的特点，且要满足处理效率要求，又不能依赖大量可信的训练数据。

2 基于AR（n）预测模型的风机实时监测数据处理方法

本文利用监测对象本身的一组观测数据之间的关系来描述监测数据随机变动的规律，即建立AR（n）线性自回归预测模型。给出监测数据的预测模型参数及其机制，以预测未来时刻的值，用预测值和监测值比较的方法确定异常值。

AR（n）预测模型的建立不需要预先设定参数值，只需少量近期正常监测数据和简单计算就可以估计模型的参数并能实时给出预测值，比较适用于监测数据种类多、格式复杂、信息量大的海上风机异常监测数据的实时处理。

结合相关研究文献，为了降低预测误差，本文采用预测模型参数自动调整策略，以便在预测误差超过预先设定的阈值时，通过相应计算就可以估计模型的参数并能实时给出预测值并实时自动调整预测模型。

2.1 AR（n）模型异常数据处理机制N个样本点与xt的线性关系为：是不可观测的随机变量。即：

式中：βi为自回归参数；为 εt的方差［5］。

将{xt}序列直接代入式（1），可以得到线性方程组，用矩阵形式表示为：

根据多元回归理论，参数矩阵β的最小二乘估计为：

对AR（n）模型，拟合的方法有很多，根据相关研究成果，其中Box拟合方法简单，且具有较快的拟合速度，尤其适用于对模型阶次毫无任何验前信息的情况［5-7］。该拟合方法在做最小二乘估计时，从n=1开始对{xt}开始拟合AR（n）模型，检查最后一个自回归系数βn，如果βn≈0，则确定适用模型为AR（n-1）。

根据AR（n）模型的性质知［8］，其模型的误差值，即满足标准正态分布。为使 εt尽可能为0，在预测过程中AR（n）模型应自动调整相关参数。当εt=0出现的概率小于一个阈值时，模型就需要调整。设当前时刻的预测误差为εt，预测误差期望值为E（εt），设调整后的误差为ε′t，要使ε′t尽可能为0，可将 εt-E（εt）的值近似为ε′t，即ε′t=εt-E（εt）。

用 βi代替，用ε′t代替εt-E( ) εt，则原模型可改写为如下形式：

即为调整后的预测模型。综合相应的研究成果［9-10］，给出如下调整方案：针对每次的误差值εt，计算 P（εt=0），即计算εt=0出现的概率；如果P（εt=0）＜δ，δ为设定的阈值，则计算；计算；得到相应参数，结合式（4），重新构建预测模型。

对于实际监测数据，xt可能是一个不符合普遍分布规律的数据，即异常数据。此时，如果用xt去预测 xt+1，xt+2，…，则会出现预测失真，为减小预测误差，采用预测值代替 xt来进行预测。虽然仍然会出现失真，但误差就会小很多。

2.2 异常数据处理方法算法编程由式（1）得且，设W为一步后移算子，即xt-1=Wxt，则可得下式：

定义：

式中：N为样本容量；ω2表示时间序列中当前时刻向前N步时刻（N为整数，且N≥1）相应预测误差εt平方和的平均值；λ表示当前误差值 εt+1的平方与ω2的比值，λ即为检测xt+1是否异常的统计量；U为预先设定的大于零的常数，当λ＞U，xt+1为异常监测数据。

在实际应用中，可根据相关传感器监测数据分布特点及实际要求而设定，假设U为0.3，则表示如果当前误差的平方和是平均误差平方和的零点三倍时，认为是异常数据。U值越大，表示监测数据中包含的异常数据的越少。一般来说，对λ＞U的情形，意味着异常值比正常值大，统计量λ的大小标志着异常点偏离正常的大小。

利用Matlab软件与Java语言按照上文所述步骤编写相应程序，实现该异常数据处理算法，具体程序框架如下图1所示。

图1 异常数据实时处理程序框架图

3 异常数据处理方法应用

利用上述方法对海上风机风速及各种传感器实测数据进行处理，验证该异常数据处理方法的有效性及适用性。由于风机塔筒无法安装风速传感器，采用风机临近的测风塔上的风速仪监测值进行分析，风速传感器安装高度为10m，采样周期为5 s，其他类型传感器包括钢筋计、倾角计、土压力计及锚索计，安装在风机基础不同位置处，采样周期均为6m in。

3.1 异常风速监测数据处理对于AR（n）模型，选择合适的样本容量和模型阶数n是至关重要的。样本容量和阶数太大，将产生大的计算量，不适合用于实时检测；但如果采用过小的容量和阶数，又不能精确的拟合监测数据。结合AR（n）模型相关研究成果［6，11］，综合考虑处理效率和可靠度，确定样本容量为160，模型阶数n为4，在此基础上，针对某时段内连续风速实测值进行分析，讨论该异常数据处理方法的适用性和有效性问题。

（1）具有自调整机制的AR（n）预测模型的有效性。对于正常风速监测数据，运用自调整系数的AR（n）预测模型，给出对应时刻预测值。预测值与实测值之间的对比结果如图2所示。

图2 无异常监测数据实测值与其预测值

图3 含有异常的监测数据实测值与预测值对比

由相关研究成果可知［10-11］，预测结果可由最终预测误差（FPL）定量评价，经过程序计算，该模型最终预测误差。一般认为，当FPE＜0.0015时，预测模型较好，预测结果比较符合实际，且预测值与实测值之间的最大误差为2.68%，大部分数据误差在1%以内。故该模型对于正常监测数据流，具有较好的精度，适用性较好。故可以用预测值代替对应时刻的实测值，不会产生较大误差。

为了验证模型对含有异常数据序列的适用与否，针对上述时间段实测风速值，人为的加入一些单个及连续的异常数据作为传感器监测值，考虑模型阶数、监测数据容量，以及传感器监测数据的实际需求，连续异常即异常事件包含数据点的个数最大为5个，因为通常情况下，连续5个数据异常时，则认为传感器自身存在问题。再次利用本文预测算法对新产生的异常数据集进行分析，结果如图3所示。

分析图3可知，预测模型能够准确对监测数据中的异常值进行处理，并及时的用预测值代替异常值进行修正，修正后的数据符合正常监测数据分布特点。

通过本文预测模型，可以得到包含异常值与不包含异常值的监测数据对应时刻的预测值，两组预测值对应时刻的差值，与正常监测数据的比值，即为预测结果差值百分比，可用PRD表示，如图4所示。

由图4可知，无论监测数据中是否包含异常数据，预测结果相差较小，对应时刻预测值最大差百分比值为4.13%，这是由于在预测过程中，异常数据被及时的用其预测值代替，所以预测结果不太会受相应异常数据的影响。

（2）预测数据个数对异常数据处理效率及有效性的影响。通过当前N个时刻的监测值，结合预测模型，可得到未来m（m=1，2，…）步时刻的数据值，m为预测数据个数，当出现连续的异常数据即异常事件时，后续异常数据预测值以前面时刻预测值为基础，预测数据个数会对异常数据处理精度产生较大影响。

由图5可知，当预测数据个数小于3时，处理误差λ逐步降低，当等于3时，误差达到最低，λ= 0.023，而以后随着预测数据个数增加，误差也随着增大，预测数据个数越多，处理误差增加越多，当处理数据个数为8时，λ=0.051。原因可能是当预测数据个数小于3时，预测数据越多，更能屏蔽只有一个时刻出现的异常监测数据，而随着预测个数的增加，算法会自动用预测出来的数据代替监测值，再去预测更远时刻的数据，经过多步预测后累积误差将会增多。

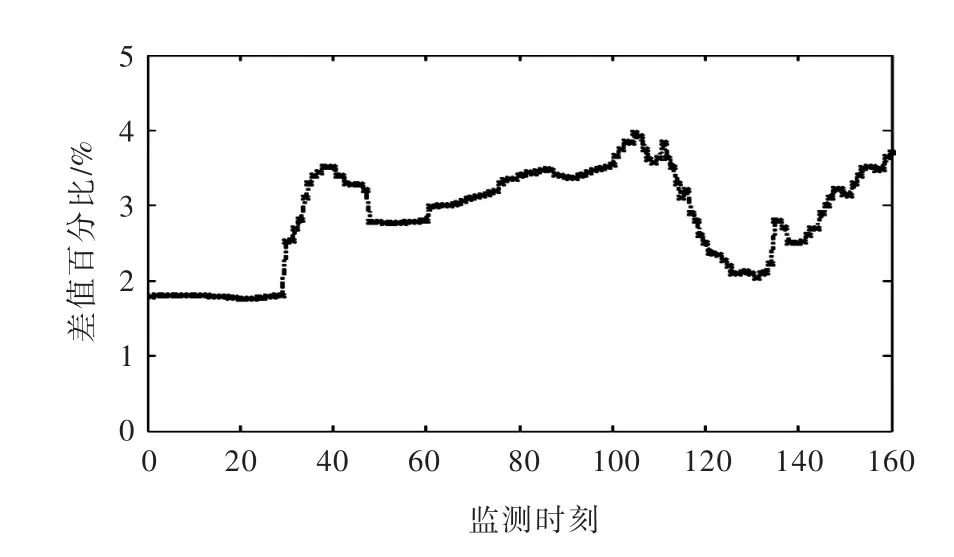
图4 有无异常数据预测值差值

图5 处理数据个数与处理误差λ关系

由图6可知，当预测数据在3个以内时，数据处理效率基本一致，效率降低不明显，当预测数据超过4个时，数据每增加一个，数据处理效率明显降低，预测8个数据的程序耗时是3个数据的将近6.5倍。要适应异常数据实时处理的要求，每次处理异常数据不能太多。

综合以上分析可知，自调整系数AR（n）预测模型对风速监测数据异常实时处理最终预测误差（PFE）为0.0006，预测值差值精度（PRD）在5%以内，运算效率也比较高；该模型能够处理的最合理的连续异常数据的个数为3个，误差最小，处理效率适中，对于正常使用情况，如果出现连续3个异常数据，则要考虑传感器自身问题或外界荷载突变引发，必须重点加以分析，数据直接进入异常数据库。即AR（n）模型对于处理时间序列的实时监测数据异常问题是有效的，其处理精度和效率相对比较高。

图6 处理数据个数与处理效率关系

表1 传感器异常数据处理特征值

3.2 各类传感器异常数据处理方法按照上文所述方法，对钢筋计、倾角计、土压力计与锚索计实际监测数据进行处理，得到相应预测值，模型最终预测误差（FPE）等特征值。用Zmax、Zmin表示正常监测数据预测值与实测值最大、最小差值百分比，用PRDmax、PRDmin表示含异常数据序列预测值与正常预测值最大、最小差值百分比。则AR（n）预测模型对应于各类传感器实时数据处理的特征值如表1所示。

分析上表可知，自调整系数AR（n）预测模型处理各类传感器实时监测数据具有相同的分布规律，如下所示：（1）模型最终预测误差（FPL）均小于0.0015，即模型对各类数据处理适用性较好；（2）利用正常监测数据得到的预测值与实测值之间的差值，能够控制在8%以内，考虑到实际工程中应用的精度问题，8%偏差在实际工程中是可以接受的，且与其他异常处理方法相比，AR（n）预测模型精度比较高；（3）含有异常值的预测值与正常数据的预测值之间的差值百分比在6%以下，即异常值预测值与该值处的正常值比较接近，可以对异常值进行替换，以保证监测数据的完整性；（4）自调整系数AR（n）对于风速监测数据，合适的数据处理个数为3，则对其他类传感器合适的数据处理个数也应为3个。

风速、应力应变、倾角、土压力及锚索等监测数据具有明显的时间连续性，监测频率固定，通过上文分析可知，对于该类监测数据序列中的异常数据，自调整系数AR（n）模型具有一定的适用性和有效性。

4 结论

本文结合海上风机实时监测数据无固定分布模型、随季节与时间变化非线性强、短时间分布及变化趋势相对稳定、数据种类多，格式复杂、信息量大等特点，建立了具有自动调整参数功能的AR（n）模型对监测数据流进行处理，该模型的实时自动调整参数机制较好契合监测数据流的特征。应用该方法对某海上风机实时采集风速及其他传感器监测数据进行了处理，结果表明，当异常数据在3个或以内时，该方法预测偏差在6%以内，最终预测误差小于0.001 5，具有较好的精度及效率，对于具有时间序列的风机异常监测数据实时处理具有一定的有效性和适用性，可以为类似工程中异常数据实时处理提供一定的参考。

［1］ 杨锦园.桥梁健康监测系统数据处理分析的研究［J］.微计算机信息，2008，24（1）：87-91．

［2］ 刘芳，毛志忠.基于小波隐马尔可夫模型的控制过程异常数据检测方法［J］.控制与决策，2011，26（8）：1187-1911．

［3］ 郑滨，任蕾.一种融合了异常数据识别的CMN改进算法［J］.计算机工程与应用，2013，49（8）：120-129．

［4］ 梁宗保，胡怡然，张凯 .桥梁健康监测信息的数据驱动处理方法研究［J］.计算机技术与发展，2013，10（20）：63-69．

［5］ 谭义红，林亚平，董婷，等 .传感器网络中异常数据实时检测算法［J］.系统仿真学报，2007，19（18）：4335-4338．

［6］ Da Silva S，Dias JNior M，Lopes Junior V.Damage detection in a benchmark structure using AR-ARX models and statistical pattern recognition［J］.J.Braz.Soc.Mech.Sci.Eng.，2007，29（2）：174-84.

［7］ Peter JBrockwell，Richard A.Davis.时间序列的理论与方法［M］.第2版.田铮，译.北京：高等教育出版社，施普林格出版社，2001.

［8］ 王国新，阎艳，宁汝新，等.数据驱动与模块化控制模型相结合的生产系统快速建模方法［J］.系统仿真学报，2009，24（14）：4224-4230．

［9］ 王家伟，汪仁红，罗宪，等 .基于数据流的桥梁健康监测海量数据处理［J］.计算机系统应用，2011，20（12）：158-161．

［10］ Datar M，Gionis A，Indyk P，et al.Maintaining stream statistics over sliding windows［J］.SIAM Journal on Co⁃puting，2001，31：1791-1813．

［11］ 王永利，徐宏炳，董逸生，等 .数据流上异常数据的在线检测与修正［J］.应用科学学报，2006，24（3）：256-261．

Study on the approach to dealing with the abnormal data in real-time monitoring of the offshore wind turbine

ZHOU Jianhua1，LÜPengyuan2，WANG Chun1
（1.Beijing IWHRCorp.，IWHR，Beijing 100048，China；
2.XiangshuiYangtzeWind Power Generation Co.，Ltd.，Yancheng 224600，China）

s：It has very important significance for the fan structure function analysis and evaluation of the se⁃curity state to disposes the monitoring data of the offshore wind turbine in real-time.At the present stage，the methods for processing abnormal data in real-time should be improved.In this paper，the general rules of the monitoring data and the corresponding characteristics of abnormal data are obtained by analyzing the characteristics of monitoring data of the fan in real-time.The abnormal data is processed through the AR（n）prediction model，and the processing mechanism of this model is analyzed.Through appling this meth⁃od to process the monitoring data of the wind speed and a variety of sensors，it has been proved that the method is effective and applicable for dealing with the anomaly monitoring data.

the abnormal data；deal with in time；processing mechanism；AR（n）prediction model with automatic parameter ad justment

文献标识码：Adoi：10.13244/j.cnki.jiwhr.2015.04.011

1672-3031（2015）04-0306-06

（责任编辑：王冰伟）

2015-01-21

周建华（1985-），男，山东济宁人，硕士，助理工程师，主要从事海上基础研究。E-mail：future521@163.com