拖曳系统运动传递计算

王志博，侯德永

（中国船舶科学研究中心，江苏无锡214082）

拖曳系统运动传递计算

王志博，侯德永

（中国船舶科学研究中心，江苏无锡214082）

由母船、拖缆和拖体构成的拖曳系统，在拖航作业中，母船受风浪扰动发生升沉和纵摇运动，水面扰动沿缆传递至拖体，影响探测设备性能。文中研究的合理简化的母船波浪运动预报模型、结合已有的拖缆动力学计算模型耦合拖体空间运动模型，构造衔接条件和转换关系式，建立较为完整的水下拖曳系统运动传递模型。编制相应计算程序，计算了二段式拖曳方式对扰动的传递，归纳其扰动传递特性。表明该模型可应用于拖曳运动稳定的设计分析。

升沉；纵摇；拖曳系统；缆；动力学；拖体；扰动

0 引言

海洋拖曳系统由搭载母船、甲板绞车、铠装拖缆、沉降器、脐带缆、拖曳体等主要部分组成，根据探测目的选定拖曳航速和作业方式，常用的拖曳方式可分为单体重力式和二段式以及多段式。风浪流对拖曳系统的运动稳定性会产生不利影响，进而影响到水下拖体搭载探测设备的正常运行。因此在拖曳系统的设计中应当着重考虑拖曳系统对海洋环境的适应性，优化各主要组成部分的运动稳定性能。

本研究认为低速拖曳时，风浪、海流、涡激振荡、温盐差等对拖缆的直接扰动力形成的拖曳系统运动稳定性能的影响并不显著，在拖航中母船响应风浪将扰动传递到拖曳系统成为最主要的扰动因素；母船高速拖曳对风浪响应程度低，放缆长度小，涡激励振荡成为影响拖曳系统运动稳定性能的主要因素，因此工程上常采用导流套等措施消除涡激振荡的影响稳定拖体沉深。

缆索动力学问题的求解方法包括有限元法、有限差分法、集中质量法等。Walton[1]、Huang[2]等发展了集中质量法，该方法物理意义明确，算法简便，边界条件适应能力强，以此为基础，开发了适用于计算连接多个悬浮物的拖缆[2]，缆体的运动耦合[3]，拖缆触及海底[4]，以及拖曳系统对拖船操纵运动的响应，其中包括拖船变速拖曳、回转操纵[4-5]，缆的水面端受规则波作用下的母船扰动对运动的传递[3]，建立拖体运动数学模型与缆索动力学耦合[3，7]。

近期的研究工作着重发展了集中质量法，增强了其适用能力，扩展了缆触底、振荡乾端等边界条件，建立多段缆的衔接条件，对各类典型乾端运动，为开展拖曳系统扰动传递计算打下基础，但这些研究工作常以较短放缆长度（百米左右）和简化的拖体模型做为计算对象，采用均匀海流、乾端按照给定的运动规律进行规则升沉等简化的动力学边界，不以作业母船在波浪中的运动响应历程为计算输入边界，在集中质量法的应用中拖缆常简化为不承受弯矩和扭矩的柔性缆，甚至简化掉缆的惯性效应，因此不能较为合理地计算拖缆对扰动的传递。

采用有限差分法[3，7]等建立了缆与拖曳体耦合计算的模型，利用这一模型可计算重力式和二段式拖曳系统对乾端运动的响应，但对拖曳系统的扰动传递性能计算仍缺乏较系统的归纳总结提炼。

为适应搭载探测设备对拖曳系统运动稳定性要求，设备安装匹配多样化等强烈的工程需求背景，本研究应用考虑缆的弯曲和扭转力学性能有限元法[8]，建立模拟作业船舶波浪中运动的预报模型计算拖缆乾端的运动响应，同时建立拖曳体空间运动模型，从而建立起较完善的预报船缆体运动的拖曳系统运动模型。通过编制相应仿真计算程序，计算二段式拖曳方式对水面端扰动传递的响应规律。

1 缆索动力学有限元模型

拖缆可划分为一系列的无质量直线段缆元，直线段两端是节点。缆元仅模拟缆的拉伸和扭转、弯曲等结构性质，而缆的其它性质如质量、重力、浮力、流体作用力等凝集到缆元两端的节点上。缆内部的每个节点可代表相邻两个缆元特性参数之和的一半，缆两端的节点仅能表示连接缆元参数的一半。

为了便于计算缆内的弯矩和扭矩，对缆建立固定于母船的乾端坐标系，在每个节点处建立随体坐标系Nxiyizi，每一段缆元的两端各建立两个随体坐标系Sx1y1z和Sx2y2z。分别建立三个弹簧阻尼有限元模型[9]，计算获得每个节点相对位置和动力系数后，转换到乾端的坐标系Nx0y0z0中或随船坐标系中。

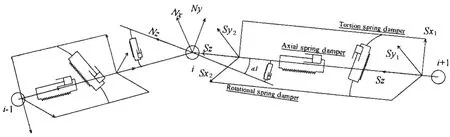
图1 缆元和节点模型Fig.1 Cable segment and node model

对于第i个缆元针对缆的结构受力建模，张力弯矩扭矩的计算模型如下：

上式中刚度项的含义是：EA是轴向拉伸刚度；ε是平均轴向应变；P是缆元承受的水压力；A=πrL0是承压面积；L0是未伸长的缆元长度；EI是弯曲刚度；有效曲率C=2·α2/L0；K是扭转刚度；τ是缆元扭转角；阻尼项的含义为：拉伸阻尼·et/100；et是缆的拉伸阻尼系数；dL/dt是收放缆速率；弯曲阻尼Ms为缆元的质量；λ是缆的弯曲阻尼系数；是动态曲率；扭转阻尼是缆的扭转阻尼系数；Iz是缆结构扭转惯性矩。dτ/dt是扭曲变化率；

在节点坐标系中，空气或水与缆相对流动速度Vr分解成平行于缆轴向的分量Vz和垂直于缆轴向的分量Vn，Vn还可进一步分解为Vx和Vy，阻力也相应地分解为Vx、Vy、Vz。对应的流体阻力系数为Cdx、Cdy、Cdz，在空气和水中取不同的值。

其中：Da是缆径，L是缆元长度。附加质量力包括缆的加速度引起的惯性力CaALVi和缆的加速运动引起的周围流体的附加质量力（1+Ca）AFVi，

其中：Ca是附加质量系数，AL是缆加速度，AF是附加质量对应加速度，Vn是缆元体积。综上所述，每个节点承受的力包括：两端的张力、两端弯矩、两个剪切力、扭转力矩等缆元的结构受力；缆的其它分布载荷力包括缆的水中重力、水流阻力、附加质量力等节点受力。将上述这些力转换为节点坐标系后求和，写成牛顿第二定律的形式：

本研究采用有限元显式求解格式，建立刚度矩阵和右端项[10]，结合边界条件，可计算缆元节点的位移和加速度，按照时间积分求和后得节点的速度和位置。缆的水面端给出运动学边界条件，拖体端给出了动力学边界条件。对于母船端指定了位移或速度：

其中：f（x,y,z,t）是缆的水面端运动；对于拖体端由拖体的重力和水流阻力以及运动姿态等给出水下缆端的受力和力矩：

2 纵摇与升沉运动模型

在风浪环境中，母船的纵摇和升沉运动是影响拖曳主要因素。一般在母船船尾实施拖航作业，需要将母船的升沉运动和母船的纵摇运动叠加在一起作为拖缆乾端的计算输入。如果不考虑船舶的进退的影响，可只认为纵摇和升沉运动耦合，建立求解波浪中母船运动的纵摇升沉运动模型，船舶在规则波中纵摇和升沉运动的数学模型为[11]：

其中：m为船体质量，Iyy船体质量对随船坐标y轴的惯性矩，azz、aθθ、azθ和aθz为船体的附加质量或附加质量惯性矩，若已知船舶的型表面，可运用求解速度势的Hess-Smith方法求解[12]；bzz、bθθ、bzθ和bθz为线速度和角速度的流体阻尼系数，根据母船初步设计阶段的设计图谱资料可获得与方程组相关的升沉和纵摇及耦合项阻尼系数；czz、cθθ、czθ和cθz为复原力和复原力矩矩系数，可查阅船舶的静水力曲线计算获得。方程组中的右端项分别为升沉运动的波浪干扰力和纵摇运动的波浪干扰力，结合船型资料利用势流理论可计算不同波长、频率和浪向角对应的波浪干扰力矩。

但是在拖曳系统初步设计阶段，往往缺乏相关的设计资料，甚至搭载母船未建造或未选定，因此需要采用简便的估算方法计算上述系数，恰当地估计船舶在波浪中的纵摇和升沉响应。对于拖曳系统而言，关注船舶拖曳运动的升沉幅度和周期，因此可将波浪简化为规则波，按照拖曳系统搭载设备工作海区海况统计资料给定波浪周期和有义波高，计算顶浪拖航情况下船舶的运动响应。为便于计算，本研究采用如下近似计算公式[13-14]：

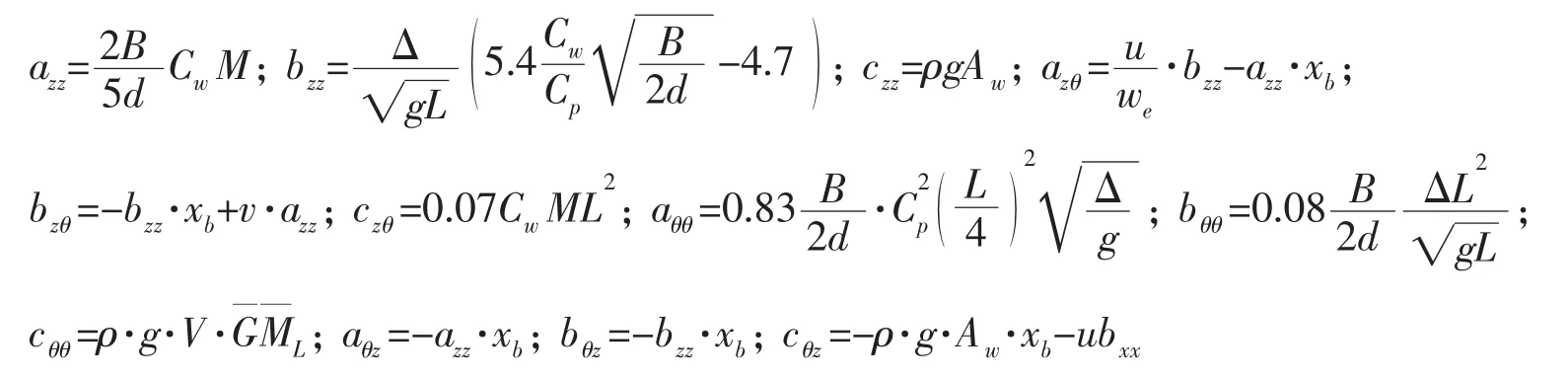
其中：B为船宽，d为平均吃水，Cp为棱形系数，L为船长，△为排水量，Aw为水线面面积，xb为浮心纵向位置，V为排水体积，为稳性高，估算关系式为：为方形系数。

2.1 波浪力的求解

规则波的波面方程为：

利用以下关系式计算船舶垂荡和纵摇的主干扰力和力矩[15]：

其中系数为

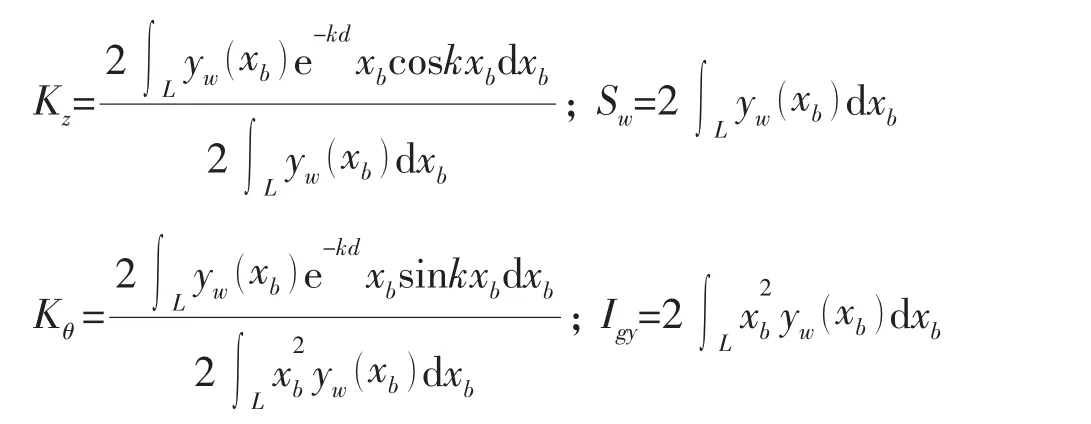
计算（9）式，需要利用母船的型线图，计算浮心所在的水线面的半宽yw（xb）值，才能求得主干扰力矩。在没有母船型线资料时，可由船长和型宽拟合为椭圆代入yw（xb）简化计算，上式中的频率ω为遭遇频率。

3 拖体运动建模

无动力拖体的重心处建立随体坐标系Oxyz，拖体的运动方程为：

其中：m为拖体的质量，Ix、Iy、Iz为拖体的惯性矩，λii为拖体的附加质量，u、v、w、p、q、r为拖体的运动线速度和角速度，X，Y，Z，K，M，N为拖体受到的力和力矩包括重力、浮力、惯性力，流体作用力、缆端张力等，六向力的表达式为：

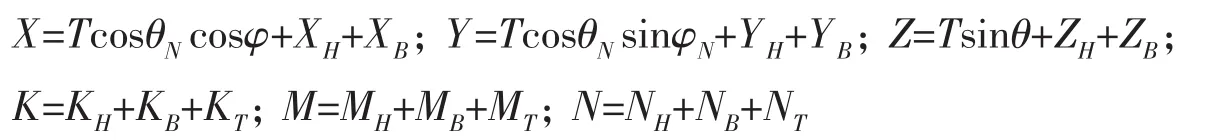
其中：下标H表示与水流作用力相关的水动力项，B表示与浮力作用相关的项，T表示与缆力作用相关的力和矩。可根据拖体的外形特征建立水动力项展开为稳定翼的水动力项和拖体主体的水动力项等，本研究将拖体的水动力系数简化为一项进行表达并以拖体的总长度对水动力进行无量纲化，例如

4 集成建模仿真

4.1 集成建模

本研究建立了船舶在规则波中的升沉纵摇运动计算模型、拖缆动力学计算模型和拖体运动计算模型。这三个计算模型集成在一起进行计算时，由于母船的重量和惯性远大于拖曳系统本身，本研究不考虑拖曳系统对母船运动的影响，利用船舶升沉纵摇运动计算模型计算获得母船甲板绞车处的合成扰动为：

4.2 坐标系的变换

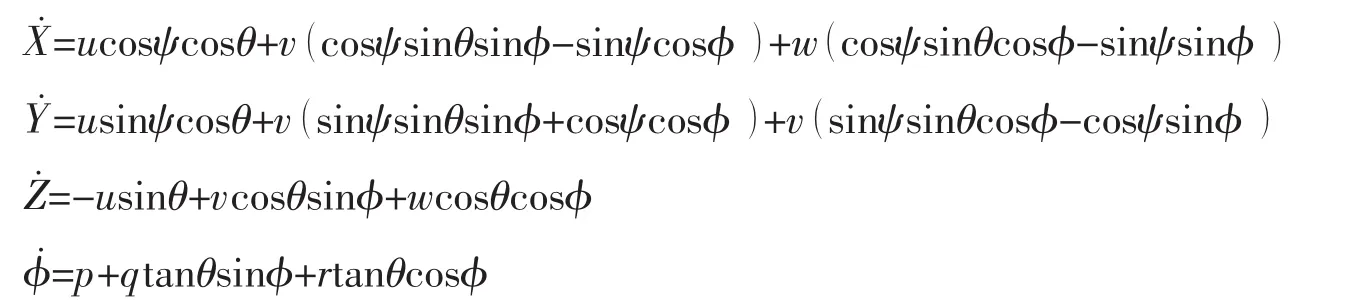
（12）式左端项表示拖体的运动转换到缆体系中的线速度和角速度。

5 计算实例

为考核本文建立的模型的可行性，根据上述建立的扰动计算模型，编制计算机求解程序，对由母船、主拖缆、沉降器、脐带缆和微浮力的拖体构成的的二段式拖曳系统进行计算扰动传递与衰减的情况。船舶升沉纵摇模型参数为：

B=12 m，d=8.6 m，Cp=0.74，L=78 m，△=3 150T，Aw=54.6 m2，xb=0.78 m，Cb=0.63；波浪参数A=3.0 m，t=8.0 s，计算时长为160 s。主拖缆缆径d=21.6 mm，主拖缆不产生初始扭转张力，因此保持低水平的缆内扭转力矩，参数如表1所示。

表1 主拖缆参数Tab.1 Main towed cable parameters

中性脐带缆主要克服中性拖体的阻力，可简化认为是柔性缆，缆径d=31.5 mm计算参数如表2。

表2 脐带缆参数Tab.2 Umbilical cable parameters

拖体运动模型参数为吊点安装位置xw=50.3 m、yw=0 m、zw=2.0 m，对拖体而言在拖体型表面划分缆元，可利用Hess-Smith方法计算λii′的值，利用计算流体力学分析或水池试验可获得拖体的相关水动力系数的值。1＃和2#拖体外形均为流线型，1＃拖体为重力式拖体，2#拖体为弱浮力型拖体，利用拖体总体布置方案计算总体质量特性和拖曳力臂、浮力臂等参数，在此不做详述。根据以上参数对此二段式拖曳体进行扰动传递计算。

5.2 计算结果分析

（1）采用本文给出的母船顶浪纵摇与升沉的运动响应预报模型计算得到船舶重心处纵摇响应历程和升沉响应历程见图2和图3，预报模型显示了船舶在规则波中纵摇和升沉的历程和响应特点。乾端传递运动因绞车安装于船尾位置（图4），放大了扰动作用。

（2）图6和图7显示1#拖体的运动与母船升沉纵摇运动幅度和周期基本一致，对母船具有跟随一致性；图8和图9显示采用脐带缆连接的2#拖体，由脐带缆传递而来的扰动力迅速衰减，数值求解拖体的运动方程组得到2#中性拖体纵摇角幅度小于±3°，说明二段式拖曳方式可理想地消减母船传递的扰动，1#拖体对运动传递具有良好的阻尼作用。根据实测2#拖体的运动记录分析，相似海况时纵摇幅度统计值接近±3°，说明该模型预报结果较为合理。

（3）图10显示主缆弯矩在近水面端和近拖体段有显著的增加，这是由于水面拖曳力、水流阻力累积效应，以及拖体阻力的联合作用形成，在弯矩较集中的两端，可对缆采取适当的防护。图11显示主拖缆乾端张力水平较高，随母船的升沉，张力发生了显著的增大，不利于拖缆的安全性，应当采取恒张力保护措施。

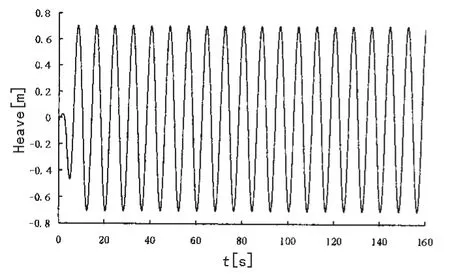
图2 船舶重心升沉Fig.2 Gravity center heave motion

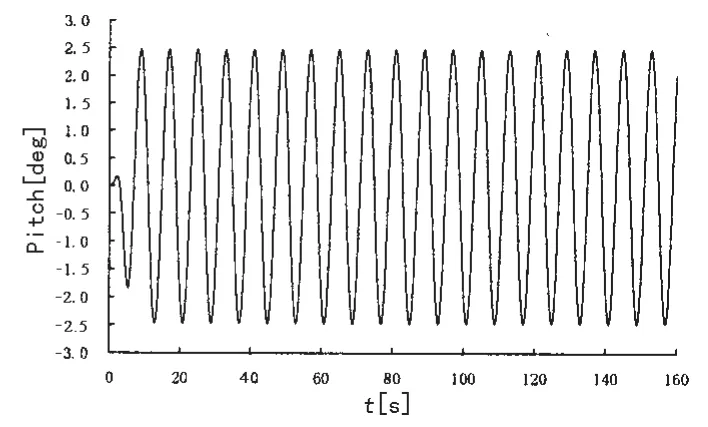
图3 船舶重心纵摇Fig.3 Gravity center pitch motion

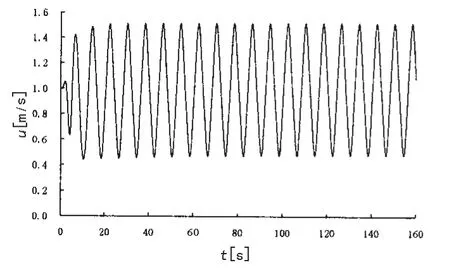
图4 乾端拖航速度Fig.4 Surface top towing speed

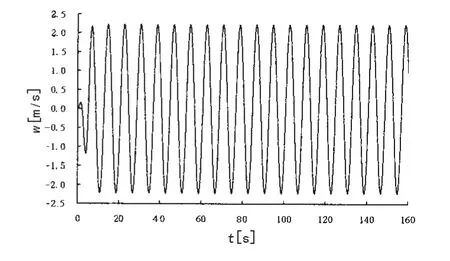
图5 乾端升沉速度Fig.5 Surface top heave speed

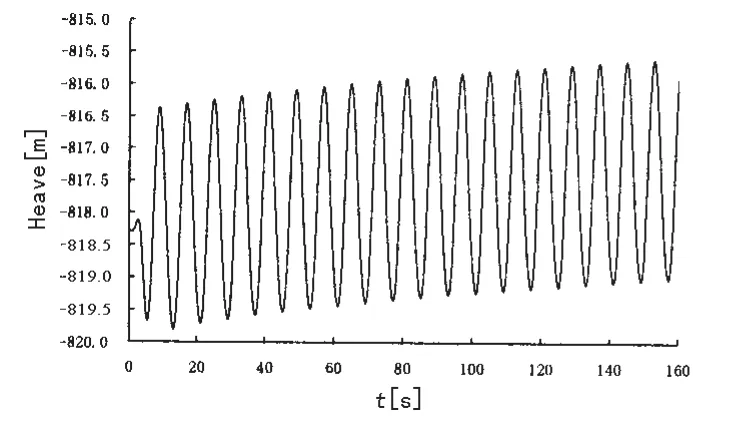
图6 1#拖体端升沉Fig.6 1#towed body heave motion

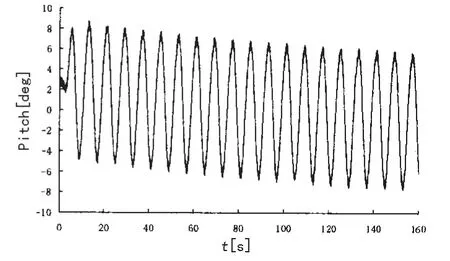
图7 1#拖体端纵摇历程Fig.7 1#towed body pitch motion

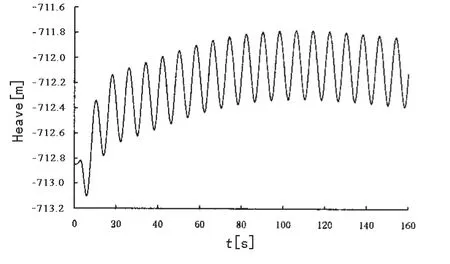
图8 2#拖体端升沉Fig.8 2#towed body heave motion

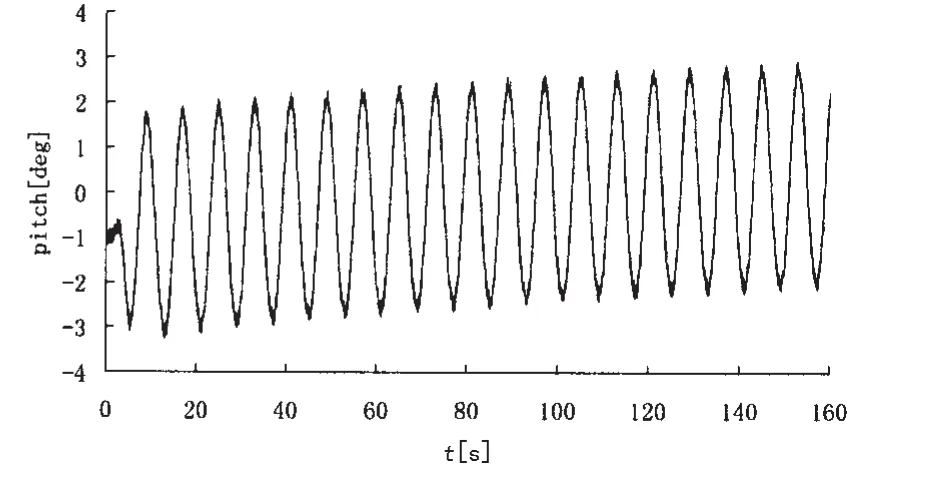
图9 2#拖体端俯仰Fig.9 Towed heave motion of 2#

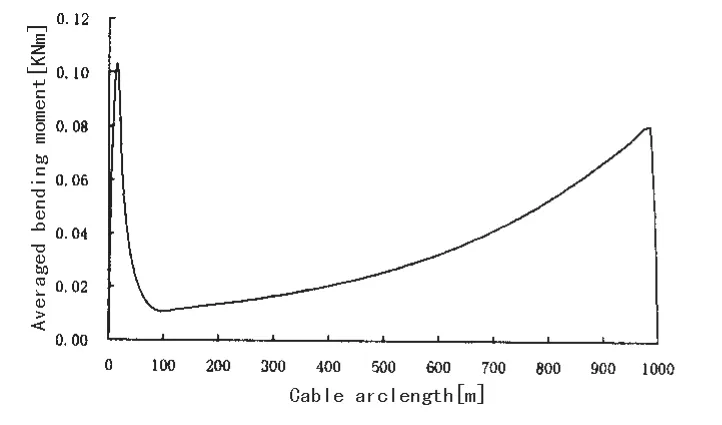
图10 主拖缆缆内弯矩分布Fig.10 Main towed cable bend moment

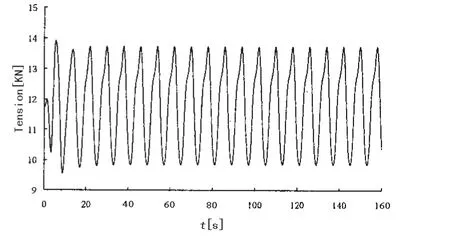
图11 主拖缆乾端张力时间历程Fig.11 Surface top tension of main towed body

6 结语

本文应用可计算缆内弯矩和扭矩的缆索有限元模型，构造衔接条件和转换关系式，建立了包括作业船舶、拖缆和拖体运动模拟模型在内的较为完整的拖曳系统扰动传递计算模型，可应用于拖曳运动稳定的设计分析。本研究在后续工作中还将建立船舶在随机波浪序列中的运动响应预报模型，完善所建立的拖曳运动预报模型，使拖曳系统运动预报更加符合实际。

[1]Walton T S,Polachech H.Calculation of transient motion of submerged cables[J].Mathematics of Computation,1960,14: 27-46.

[2]Huang S.Dynamics analysis of three-dimensional marine cables[J].Ocean Engineering,1994,21(6):587-605.

[3]Wu Jiaming,Allen T.A hydrodynamic model of a two part underwater towed system[J].Ocean Engineering 2000,27(2): 455-472.

[4]王飞.海洋勘探拖曳系统运动仿真与控制技术研究[D].上海:上海交通大学,2007:71-73. Wang Fei.Research on kinetic simulation and control of ocean towed system[D].Shanghai:Shanghai Jiaotong University, 2007:71-73.

[5]罗薇,张攀.水下拖曳系统运动预报[J].武汉理工大学学报,2007,29(6):139-142. Luo Wei,Zhang Pan.The motion prediction of motion of towed system[J].Journal of Wuhan University of Technology, 2007,29(6):139-142.

[6]朱克强,李道根,李维扬.海洋缆体系统的统一凝集参数时域分析法[J].海洋工程,2002(2):100-104. Zhu Keqiang,Li Daogeng,Li Weiyang.Lumped parameter analysis method for time domain of ocean cable body systems [J].Ocean Engineering,2002(2):100-104.

[7]李英辉,李喜斌,戴杰.拖曳系统计算中拖缆与拖体的耦合计算[J].海洋工程,2002,20(4):27-42. Li Yinghui,Li Xibin,Dai Jie.Calculation of coupling between the cable and the towed body in the towed system[J].O-cean Engineering,2002,20(4):27-42.

[8]Sun F J,Zhu Z H,Rosa M La.Dynamics of cable towed body using nodal position finite element method[J].Ocean Engineering,2011,38(1):529-540.

[9]OrcaFlex Manual[M].Orcina Ltd,2012:161-167.

[10]曾攀.有限元分析及其应用[M].北京:清华大学出版社,2004:91-99. Zeng Pan.Finite element analysis and its application[M].Beijing:Tsinghua University Press,2004:91-99.

[11]陶尧森.船舶耐波性[M].上海:上海交通大学出版,1985:53-57. Tao Yaoseng.Ship seakeeping[M].Shanghai:Shanghai Jiaotong University Press,1985:53-57.

[12]戴遗山,段文洋.舰船在波浪中运动的势流理论[M].国防工业出版社,2008:28-35. Dai Yishan,Duan Wenyang.The ship motion in waves in potential flow theory[M].Beijing:National Defense Industry Press,2008:28-35.

[13]Zhang xinguang,Zou zaojian.Application of wavelet denoising in the modeling of ship manoeuvring motion[J].Journal of Ship Mechanics,2011,15(6):616-621.

[14]李子富,杨盐生.船舶在规则波中纵摇与升沉运动的仿真[J].大连海事大学学报,28(4):13-16. Li Zifu,Yang Yansheng.Simulation of the heaving and pitching motion of ship in regular wave[J].Journal of Dalian Maritime University,28(4):13-16.

[15]吴秀恒.船舶操纵性和耐波性[M].北京:人民交通出版社,1988:195-197. Wu Hengxiu.Ship manuverbility and seakeeping[M].Beijing:China Communications Press,1988:195-197.

Towed system motion transfer calculation

WANG Zhi-bo,HOU De-yong
(China Ship Scientific Research Center,Wuxi 214082,China)

The towed system includes towing ship,cable and towed body.The main disturbances come from towing ship’s heave and pitch motion induced by sea wave and wind.Sea surface disturbances are transferred along cable to cause towed body bad performance.The reduced ship motion mathematical model, cable dynamics model,and towed body motion model are initially integrated as a new disturbance propagation model by connection conditions in this paper.A computer program simulates the surface regular wave disturbance propagation property of two part towed system according to the model.The integral method can be used in the design of sea towed system.

heave;pitch;towed system;cable;dynamics;towed body;disturbance

P756.1

A

10.3969/j.issn.1007-7294.2015.04.006

1007-7294（2015）04-0389-08

2014-12-05

王志博（1983-），男，博士研究生，工程师，E-mail:wwzb3@163.com.cn；侯德永（1966-），男，研究员。