基于多任务分析的空天飞行器综合效能评估

熊 嵩，周 军，呼卫军，卢 青

(西北工业大学 精确制导与控制研究所， 西安 710072)



基于多任务分析的空天飞行器综合效能评估

熊 嵩，周 军，呼卫军，卢 青

(西北工业大学 精确制导与控制研究所， 西安 710072)

空天飞行器效能的评估必须与实际任务相结合才更有意义。提出了基于多任务分析的效能评估模式，实现了对任务需求具有较强敏感性的动态权重评估方法。首先构建下层神经网络法与上层层次分析法的混合评估模式，然后通过对任务内容关注度与任务阶段优先级的度量，实现任务层权重的修正。评估后的指标求解算法分析了方案的改进需求。单方案评估与多方案对比的算例表明，多任务分析效能评估不仅能够衡量空天飞行器的基本能力，而且能够充分反映其基本指标对于不同类型任务的适应程度，从而为指定任务下的指标方案论证与优化提供参考方向。

空天飞行器；效能评估；任务模型；动态权重

0 引言

空天飞行器(Aerospace Vehicle, ASV)作为快速发展的前沿太空武器化装备，其多用途、高重用、快速应变的特点使得其优势越来越明显[1-2]，对空天飞行器的方案论证随之成为一项重要课题，而效能评估是完成其立项论证的主要途径[3]。

目前，针对ASV的效能评估主要集中在传统评估理论的应用，如文献[4]分析了目前主要的效能研究方法的基本分类、过程、量度以及各自的特点，文献[5-7]则是专家评判法、灰色层次分析法、神经网络法等应用于ASV评估的具体案例。但对于方案论证而言，评估的意义更多地体现于ASV对于不同任务、不同关注点、不同需求度的综合效能[8]，需要对任务的侧重点具有足够的适应性。

当前面向任务的效能评估已反映于多种作战系统评估中。国外的Robert A M、David J P 等学者把对任务效能的要求与飞行器的结构设计、参数配置等绑定[9-10]；国内的张建康、陈晨等学者则尝试将不同任务映射到不同的指标集合，并确定各自的影响度[11-12]。

本文重点在于结合ASV未来主要的任务模式，以关注度与优先级概念为基础实现适用于不同任务要求的动态修正权重评估算法，并进行任务概念模型设计、方案改进需求分析等研究。

1 基于ASV任务模式的评估过程

作为涵盖航空、航天领域的多用途武器平台，空天飞行器的工作模式可概括为3类：

(1)在轨运行：飞行器以轨道飞行过程为依托，长期在轨执行对地监测、信息收集、反航天器攻击等天基任务。

(2)一次性再入：飞行器变轨再入大气层，执行对地的快速直接打击或单次运输等任务。

(3)重复性往返：飞行器以地基与天基双平台为依托，多次往返于两者之间，执行可重复的载荷投放、天地运输等任务。

显然，不同工作模式对于ASV的任务要求有相似点，任务之间存在耦合。面向任务的ASV效能评估需要基于任务的分解模型实现，过程如下：

步骤1 任务解析：包括子任务的分解与底层指标集的映射，前者将主任务分解为多个子任务，后者则对每个子任务明确其包含的可度量指标。

步骤2 指标度量：建立任务型指标体系，并为各级任务确定物理度量与评判度量模型。

步骤3 权重修正：采用不同算法分析上、下层的基本权重，然后分析可能存在的关注任务因素，建立各任务与关注因素的对应关系并设计动态权重模型，是整个评估过程的重点。

步骤4 评估计算：基于动态权重模型设计评估算法，设置待评估的任务参数并计算总体效能。

步骤5 方案改进：根据评估结果，分析方案的可优化空间及对底层指标的要求。

2 面向任务的评估体系度量模型

2.1 ASV多任务解析模型

以目前ASV的主要发展方向选择4项主任务：反航天器攻击M1、对地攻击M2、投放式运输M3、着陆式运输M4。分解各自的子任务集为

M1={探测，轨道机动，跟踪，打击}；

M2={探测，再入，弹道机动，突防，打击}；

M3={再入，弹道机动，载荷释放}；

M4={再入，弹道机动，能量耗散，着陆}。

包含主观与客观参数的子任务元素集为

SMi={关注度a，优先级p，指标集T}

其中，i=1, 2, …为子任务编号。元素含义如下：

(1)关注度a：该元素反映不同评估对于各类型任务的不同侧重程度。

(2)优先级p：该元素反映子任务的逻辑顺序与执行阶段性质对于整个任务的影响。

(3)指标集T：该元素反映与子任务直接对应的底层指标集，包括指标项与指标范围要求两部分。

2.2 任务型指标体系构建与度量

根据前述任务模型，面向任务的ASV综合评估体系由总体效能、主任务、子任务、底层指标组成，上下层元素为一对多或多对多连接关系。按照系统性、准确性、可行性的要求选择底层指标，整合得到指标体系如图1所示。

图1 ASV综合效能指标体系Fig.1 Comprehensive effectiveness index system for ASV

显然面向任务的指标体系是高度耦合结构。根据ASV解析模型，分别以E、M、SM、T表示总体、任务、子任务、底层指标，则各层集合关系为

(1)

式中a与p分别为所在任务的关注度与优先级。

以权重和为基本方法的各层指标度量模型为

(2)

式中w为各指标项权重；A为任务内容的关注度矩阵；P为任务阶段的优先级矩阵，两者是权重计算的重要参数；Rk为第k个底层指标的归一化标准。

3 关联任务需求的分层权重设计

分析评估体系可知，上下层权重有明显区别：

(1)下层与上层的评估性质不同，下层指标可根据真实数据量化得到，为定量评估；而上层指标由主观评判得到，为定性评估。

(2)对于下层权重，理论上9个子任务与16个下层指标间存在着9×16=144个权重，传统算法实现复杂，而且大量的专家评定会引入主观因素。

(3)对于上层权重，待确定的权重大幅减少，允许采用专家评定思路实现。同时，为了使评估对不同任务需求点有足够的敏感性，需要量化ASV任务可能存在的需求因素，作为影响权重的动态参数。

基于这种区别将权重设计分解为两部分，采用径向基函数(Radial Base Function, RBF)神经网络模拟下层权重，采用层次分析法(Analytic Hierarchy Process, AHP)确定上层基本权重，并根据任务需求对其修正。

3.1 下层定量型模拟权重设计

所谓“模拟权重”是指通过搭建神经网络并加以训练后，利用该网络代替由下层指标到上层指标专家打分的过程。它相当于模拟了对下层指标的加“权”求和，只是 “模拟权重”是不透明的。神经网络评估的优势在于：通过海量的样本训练，得到的模拟权重能够消除专家打分方式的主观因素。

RBF网络是以函数局部逼近理论为基础，以径向距离为激励参数的神经网络，其优点是具有最佳逼近的特性，且无局部极小问题存在。针对ASV下层评估体系，RBF网络的输入层(底层指标)与输出层(子任务指标)元素数目分别为12与9，中间层元素根据经验设置为7，如图2所示。图中，cj为隐藏层的中心点数据向量。

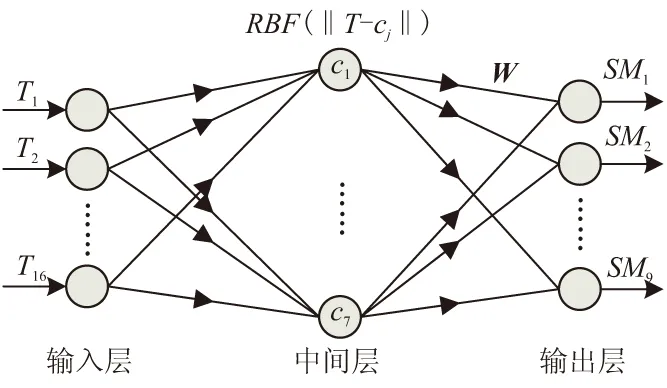
图2 神经网络评估结构Fig.2 Structure of neutral network based evaluation

中心点的输出RBF(x)即为径向基函数，这里选择高斯函数形式：

(3)

利用RBF神经网络实现模拟权重的评估需要经过3个步骤：首先，构造训练神经网络所需的大量样本，其中输入层数据通过实验得到，输出层数据可通过专家灰度打分得到；然后，基于一定的训练方法[13]进行网络训练，得到网络内部的cj等参数；最后，在实际评估应用中，在输入端输入底层指标，即可在输出端计算得到子任务层指标。

3.2 上层定性型动态权重设计

3.2.1 权重基本值确定方法

以AHP法计算上层权重基本值的基本思路是对于同一指标集内的每个指标作两两对比，模糊确定两者的相对重要程度，并以一定的数值进行衡量。对于A、B两指标，若A比B重要，以bab表示A对于B的重要程度，以其倒数表示B对A的重要程度。对于包含N个元素的指标集，其重要度判断矩阵为

对B的特征向量W归一化处理，即可得到子任务层至总体层各指标集的各项映射权重取值。

对于不同任务的影响，对基本权重的修正主要考虑2种因素，即“关注度”与“优先级”。前者考虑任务内容，而后者考虑任务阶段。

3.2.2 任务内容关注度修正参数模型

关注度是评估过程中对任务内容的侧重点的量化表示。对ASV的典型因素进行分析：

(1)任务功能类型。ASV的任务可按照功能进行基本分类，这里简单划为信息、飞行、作战3类，并设置关注度功能属性af，其取值设为1和0。以反航天器攻击为例，其3类子任务集分别为{探测}、{跟踪，机动}、{打击}。若当前关注的任务功能包括信息与作战，则探测/打击任务af=1。

(2)所需资源类型。ASV各任务的完成需要一定成本，其资源的形式是多样的，这里将其分为物质、能量与技术，并设置资源属性ar。仍以反航天器攻击为例，3种资源的子任务集分别为{打击}、{机动}、{探测，跟踪}，若当前关注物质资源，则打击任务的ar=1。

(3)直接取舍要求。有些情况下根据评估的最终目的可直接确定是否关注某任务(特别是针对主任务)，据此设置取值属性an，如果对该任务表示关注取值为1，直接舍弃则为0。

设计关注度修正参数a的模型为

a=fa(af,ar,an)

(4)

3.2.3 任务阶段优先级修正参数模型

优先级是对子任务执行阶段在整个执行过程中的地位的量化表示。以对地攻击任务为例，其执行过程如图3所示。

图3 对地攻击执行过程Fig.3 Execute process of air-ground attack

分析该过程可知， ASV任务过程中的不同子任务阶段存在以下几点典型区别属性：

(1)串行性(串行/并行)：该属性反映了子任务之间执行过程的关联性。对于子任务A、B，可能A是B的先决条件，如探测与再入，称为串行；也可能两者的前后约束相同，如机动与突防，称为并行。相对而言，并行任务的瓶颈约束较小。

(2)连续性(连续/离散)：该属性反映了子任务在时间上的持续性，例如再入飞行属于连续任务，其他为离散任务。连续任务一旦出现意外就会导致整个任务失败，而离散任务则允许组织第二次执行，可见两者的影响不同。

(3)确定性(确定/随机)：该属性反映了子任务受随机条件的影响程度。为完成对地打击，必须通过探测、再入、打击等一系列动作而实现，这些子任务是确定的；相反，机动与突防是随机的，是否执行取决于探测信息与决策。

分别以ps、pc、pa表示以上3种属性，对各属性的选择与影响程度的界定由人为主观决定。以串行性为例，若优先考虑串行任务，则探测的ps=1，机动的ps=-1，若不考虑该属性则取值均为0。设计优先级修正参数p的模型为

p=fp(ps,pc,pa)

(5)

3.2.4 动态权重修正算法

作为权重的修正参数，关注度c与优先级p的计算模型根据需要人为设置，但需满足3点要求：

(1)允许不同子任务具有相同的关注度或优先级。

(2)两参数对权重的修正能力应当有限，不能覆盖原权重的影响。

(3)两者的取值范围具有一定弹性。各任务项的权重修正算法为

w′=(a+p)w0

(6)

式中w0为根据第3.2.1节算法得到的基本权重。

由于系数a、p的添加会影响到权重的取值范围，因此需要对修正权重进行归一化处理，即

(7)

式中i为任务编号；N为任务集的元素数目。

4 提升效能方案的底层需求分析

完成方案评估后希望能够分析对原方案的优化方向，即提升总体效能方案对于底层指标的需求。对该问题的描述为：已知某ASV的指标组成，在部分底层指标不变的前提下，欲将总体效能指标提升到较高值，求剩余底层指标取值。其数学描述为：已知函数模型M=f(u1,u2,…,um)与若干自变量ui，求剩余自变量的取值。

由于体系组成复杂，直接建模与求解都较为困难，而遗传算法可解决该问题。该算法的基本思想是对大量参数值进行交叉变异，实现全局搜索，适合求解多参数优化问题。遗传算法的基本方法参考文献[14]，应用于指标反解优化的步骤如下：

(1)确定种群大小N、交叉算子s等参数；

(2)设定初始种群x=(x1,x2, …,xN)，种群中任一染色体向量包含所有待优化的底层指标；

(3)以各染色体向量为输入指标，计算该组底层指标的评估误差；

(4)计算适应度与新染色体，以各染色体期望输出与实际输出效能偏差为适应度，保留满足适应度要求的染色体，对不满足的染色体根据交叉算子进行两两交叉变异；

(5)若当前种群最优个体满足误差精度或迭代终止条件则结束优化，否则转向步骤4。

5 算例与分析

5.1 基本评估权重计算

(1)训练下层神经网络：根据已有的ASV实验数据，对参数进行一定区间的随机浮动，得到50组16项底层指标后，由专家根据灰度打分的方法得到各组对应的9项子任务指标。将这些底层指标与对应的子任务指标作为50组网络训练样本，对底层RBF评估网络进行训练，得到7个隐藏层节点的高斯宽度与输出权重分别为

R=[0.411,0.614,0.566,0.627,0.799,0.497,0.711]

W=[0.158,0.197,0.110,0.244,0.055,0.068,0.167]

数据中心值c由于数目较多不再列出。

(2)计算上层动态权重：基于AHP法得到9个子任务至4个主任务的中层传递权重矩阵为

主任务至总体效能的上层权重向量为

WM=[0.250 0.250 0.250 0.250]

5.2 飞行任务仿真算例

选取在研的某3种空天飞行器为对象进行飞行过程仿真，其中第2种飞行器不具备地面着陆能力。设定4种飞行任务过程如下：

(1)反航天器打击：敌方某弹道导弹进入中段飞行，ASV搜索、锁定目标后发射EKV弹头拦截。

(2)对地攻击：敌方某海上机动部队侵入领海，且该部队具备防空能力，由ASV再入大气层后有效规避其防空火力，最终将其摧毁。

(3)投放式运输：由ASV高速进入敌方领空，满足投放条件后将己方所需物资释放到指定区域。

(4)着陆式运输：ASV携带天基平台载荷，再入大气层后耗散多余能量并着陆于机场。

对3种飞行器分别针对不同任务执行50次随机仿真，统计各任务下的成功率。如图4。

图4 各种飞行器在不同任务下的成功率Fig.4 ASVs' success rate for different missions

根据飞行过程数据计算底层指标，提取各自指标的均值得到3套ASV指标方案如表1。

表1 ASV多方案底层指标参数Table 1 Bottom index values of the ASV examples

5.3 单方案综合效能评估

以方案1为算例对评估方法进行验证。在不考虑关注度与优先级影响的前提下，易求得该方案的总体效能为E=0.634。

为了验证不同底层指标的影响程度，以原方案参数为基础，分别选择控制误差、机动范围、弹道约束、末端约束等4个指标为[0, 1]区间变化的浮动指标，则其对应的总体效能变化区间分别为(0.6, 0.85)、(0.65, 0.8)、(0.65, 0.75)、(0.74, 0.77)。可见对总体效能的影响最大与最小的指标分别为控制误差与机动范围。分析指标体系可知，控制误差为跟踪、机动、再入等3项任务的共享指标，而末端约束为能量耗散的独有指标，说明共享指标具有更强的影响力。

考虑关注度与优先级的影响。假定关注度中功能属性的重要性较高，而优先级中各项属性的重要性相同，同时关注度的重要性比优先级高。根据第3.2.4节要求设计关注度a与优先级p模型

a=0.75(1+3af)(1+0.5ar)an

(8)

p=0.25×2ps+pc+pa

(9)

为了使结果更直观，分别设计若干关注度与优先级分布，测试其总体效能如表2、表3。

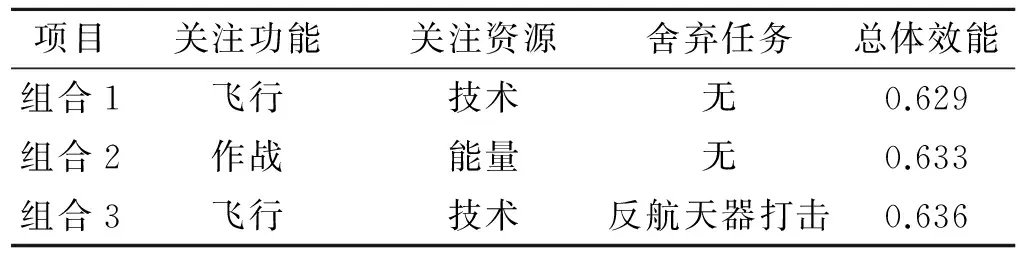
表2 不同关注度组合下的效能分布Table 2 Efficiency with different combination of attention

表3 不同优先级组合下的效能分布Table 3 Efficiency with different combination of priority

可以看出，对于关注度与优先级的不同考虑，评估体系能够有效区分其影响，同时对比结果反映了不同任务效能的优劣，如“反航天器打击”任务效能较低(图4中反航天器打击的成功率也证明了这一点)，“离散”类任务效能优于“连续”类。

5.4 多方案效能对比与优化

对方案2与方案3进行对比。根据基本评估算法，得到2个方案在不考虑权重修正情况下的总体效能指标分别为0.706与0.720。分析两方案可知，方案2在许多子任务中占优，但由于缺乏着陆能力，导致其综合能力受到抑制。如果考虑评估的关注点，对比结果会随之变化。采用表3中的3项关注组合，相应的对比结果如图5。

图5 方案2、3在不同关注度组合下的对比Fig.5 Comparison of project 2 and 3 with different attention

图5中各子项附加编号为其对应效能值较高的方案。由图5可知，在指定的关注度要求下，方案2自身的飞行作战等能力完全可弥补其着陆缺陷。

进一步，采用遗传算法计算方案3的底层指标改进需求。以关注度组合1的情况为例，已知方案2、3的总体效能值分别为0.743和0.699，假定欲通过提升导航误差与控制误差2个指标使方案3达到方案2的总体效能。以神经网络的样本构造待求解指标的初始种群，以效能输出与0.743的差值为适应度，染色体长度为2，迭代求解20次，其适应度变化如图6。

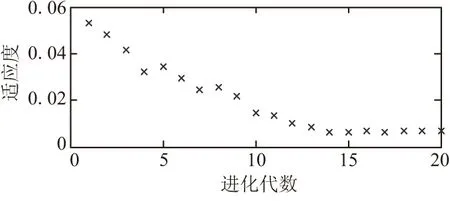
图6 最优适应度变化过程Fig.6 Changing process of best fitness

由图6可见，迭代至14次时已基本收敛至最优解，最终得到导航误差指标0.84、控制误差指标0.63，可作为提升方案3的参考方向。

6 结束语

空天飞行器的效能评估必须与实际的任务需求点与侧重点结合才更有意义。本文创新性地建立了关注度与优先级的概念与量化模型，并将其与任务分解模型的度量绑定。结合不同的关注模型，该评估能更好地说明空天飞行器自身效能对不同类型任务的适应度，从而使评估结果更具有针对性。该评估方法在一些细节如关注度/优先级模型的设计标准、关注方向的筛选形式等还有待深入研究，这是下一步工作的重点。

[1] Robert A M.Establishing mission requirements based on consideration of aircraft operations [J].Journal of Aircraft,2013,50(3):741-751.

[2] Emily A L,Mark F C.Benefits of autonomous morphing aircraft in loiter and attack missions [C] //Proc.of AIAA Atmospheric Flight Mechanics Conference,Toronto,2010.

[3] Goman M G,Khramtsovsky A V,Kolesnikov E N.Evaluation of aircraft performance and maneuverability by computation of attainable equilibrium sets [J].Journal of Guidance,Control and Dynamics,2008,31(2):329-340.

[4] 张 克,刘永才,关世义.关于导弹武器系统作战效能评估问题的探讨[J].宇航学报,2002,23(2):58-66.

[5] 吴 江,罗建军.天基再入飞行器作战效能综合评估[J].火力与指挥控制,2012,37(9):185-189.

[6] 梁金登,李东旭.空间武器系统效能评估模型研究[J].宇航学报,2007,28(5):1422-1428.

[7] Rohit G,Abhishek H,Manoranjan S.Sensitivity analysis using neural network for estimating aircraft stability and control derivatives [C] //Proc.of International Conference on Intelligent and Advanced Systems,USA,2007.

[8] Nicolai L M,Carichner G.Fundamentals of aircraft and airship design[C] //Proc.of AIAA,Reston,USA,2010.

[9] Robert A M.Mission performance considered as point performance in aircraft design [J].Journal of Aircraft,2011,48(5):1576-1588.

[10] David J P,Michael D P,Brian J G.Optimizing families of reconfigurable aircraft for multiple missions [J].Journal of Aircraft,2012,49(6):1988-2000.

[11] 张建康,程龙,黄俊,武哲.基于任务的作战飞机效能评估模型[J].北京航空航天大学学报,2005,31(12):1279-1283.

[12] 陈晨,周东华,陈杰.面向任务的网络化天基信息系统连续性效能评估[J].系统科学与数学,2010,30(6):806-815.

[13] Hyontai S.An empirical improvement of the accuracy of RBF Networks [C]//Proc.of 2nd International Conference on Interaction Sciences: Information Technology,Culture and Human,Seoul,2009.

[14] Frizo V,Max M,Rene V P.Optimization of flexible approach trajectories using a genetic algorithm [J].Journal of Aircraft,2006,43(4):941-952.

(编辑：吕耀辉)

Multi-mission analysis based comprehensive effectiveness evaluation for aerospace vehicle

XIONG Song,ZHOU Jun，HU Wei-jun, LU Qing

(Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi'an 710072, China)

The effectiveness evaluation for aerospace vehicle (ASV) should be joined with the mission closely. An evaluation mode based on multi-mission analysis was proposed, and the dynamic weight evaluation was achieved,which is sensitive to mission demand. A complex evaluation with neutral network and analytic hierarchy process (AHP) was summarized, and the modified weight method was realized with the models of attention and priority of sub-missions. Furthermore, the improvement demand was analyzed with the underlying indexes' inverse computation. Evaluation examples shows that the method based on multi-mission analysis can not only measure the basic ability of ASV, but also reflect its fitness for missions of different types, which provides a valuable reference for the demonstration under special mission.

aerospace vehicle; effectiveness evaluation; mission model; dynamic weight

2014-07-21；

：2014-08-28。

熊嵩(1987—)，男，博士生，研究方向为飞行器控制与评估。E-mail:xiongsong1987@163.com

V475.4

A

1006-2793(2015)06-0764-06

10.7673/j.issn.1006-2793.2015.06.003