基于内插式永磁同步电机的新型滑模观测器设计

曹舒春

（淮南矿业集团公司潘三矿企管科，安徽 淮南232000）

0 引言

永磁同步电动机PMSM(Permanent Magnet Synchronous Motor)主磁场由转子永磁体提供，无需励磁电流，因而具有转子损耗小、定子铜耗、定子铁耗小、功率因数高、效率高、体积小、响应快和运行可靠等一系列优点[1]。近年来随着材料科学和制造技术的发展，特别是新型稀土永磁材料铷铁硼(NdFeB)的出现[2-3]，由于其具有剩磁强度高、矫顽力强等显著特点，永磁同步电机在空调、洗衣机等家用电器、数控机床，电动汽车以及航空设备等交流传动场合得到广泛应用。

由于机械式位置传感器具有成本高、受环境影响大、不易维护等缺点，因而研究永磁同步电机无位置传感器控制策略有着重要的实际意义，成为近年来的研究热点之一。随着电力电子技术、微电子技术的发展，各种高速微处理器的问世为高精度、高响应速度的控制算法实现奠定了基础，研究开发无位置传感器控制系统完全可行。

传统滑模观测器用于永磁同步电机无位置传感器矢量控制中存在着以下局限性：

（1）对于凸极性比较明显的IPMSM，直接应用传统滑模观测器提取转子位置信息会存在一个较大误差，严重影响位置信号估计的精度。

（2）传统滑模观测器实现简单，但是这种切换控制方式会在反电动势估计信号中引入大量的高频谐波分量。这些高频分量不仅会影响转子位置信息的精确提取，还会会导致实际的滑模控制系统的抖动。

（3）传统滑模观测器中采用低通滤波器从开关信号中提取出较为光滑的反电动势信号进而根据三角函数计算出转子位置角，但是低通滤波器的引入必然会带来信号的相位延迟问题。

因而研究一种适用于内插式永磁同步电机的新型滑模观测器具有重要现实意义。

1 内插式永磁同步电机EEMF模型

对于内插式永磁同步电机（IPMSM），在d-q坐标系下其电压方程可表示为：

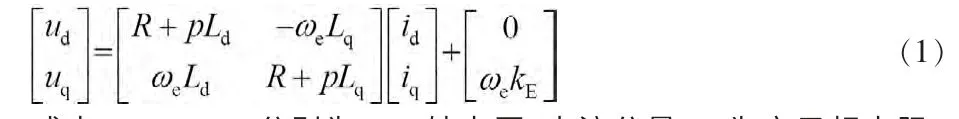
式中：ud、uq、id、iq分别为d、q轴电压、电流分量；R为定子相电阻；p为微分算子；Ld、Lq分别为d、q轴电感；kE为反电动势常数；ωe为转子电角速度。将式（1）电压方程变换到α-β坐标系，可得：

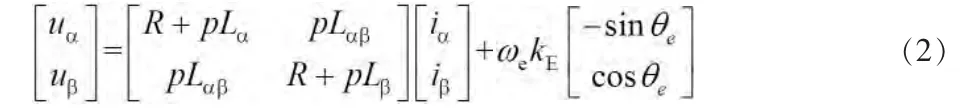
式中：Lα=L0+L1cos2θe，Lβ=L0-L1cos2θe，Lαβ=L1sin2θe，L0=1/2(Ld+Lq)，L1=1/2(Ld-Lq)。根据物理意义，式（2）右边项又可以拆分成电阻压降、电感压降以及反电动势三者之和，表示为：

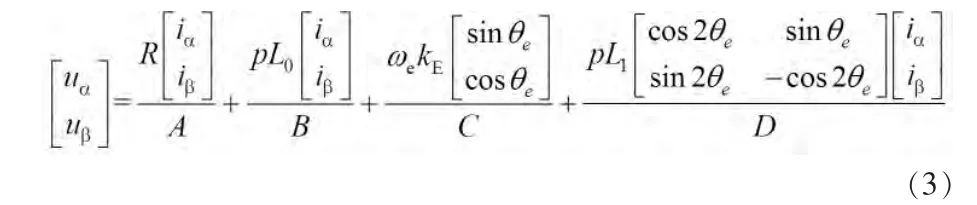
对于表面贴式永磁同步电机（SPMSM），由于交直轴电感相等，式（2）中Lαβ=0，其电压方程在α-β坐标系下可表示为：

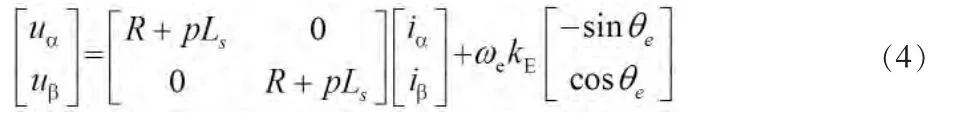
拆分成电阻压降、电感压降以及反电动势三者之和的形式，如式（5）所示。当电压与电流可以通过传感器测得时，可以通过此式得到反电动势，而转子位置信息包含在反电动势中，进而可以提取出转子位置，实现无位置传感器运行。矢量示意如图1（a）所示。

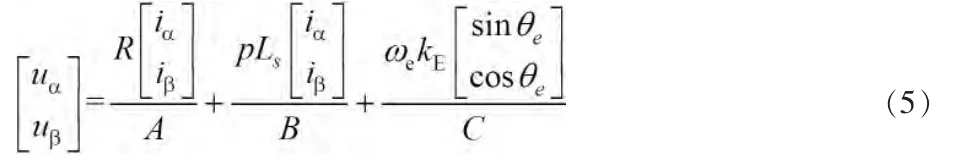
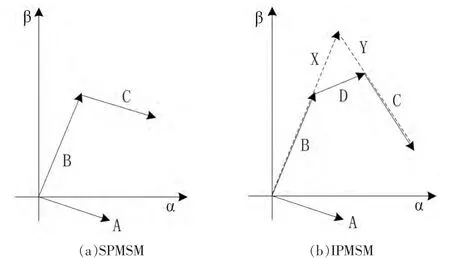
图1 矢量示意图

比较式（3）与式（5）可以看出，IPMSM电压方程中不仅含有θe的函数也含有2θe项，这与SPMSM的电压方程形式差别较大，若按照传统滑模观测器的设计方法，无法构造适用于IPMSM的观测器。与SPMSM形成差别的根本原因是IPMSM中Ld与Lq不相等，导致式（1）中右边第一项是不对称，进而旋转变换过程中包含了2θe项。将式（3）中右边部分用矢量图表示如图1（b）中的实线部分，与图1（a）中SPMSM相比多了2θe项后对于转子位置信息的提取带来很大的不便。若将式（1）改写成如下形式：

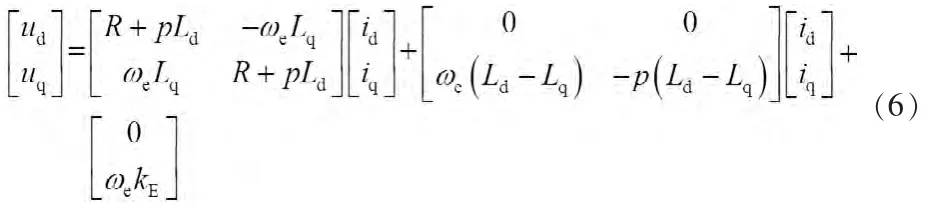
将（6）式变换到α-β坐标系下，得：

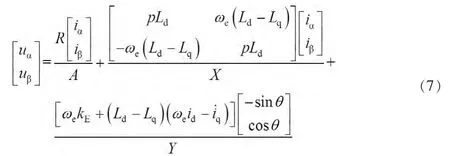
将式（7）右边部分用矢量图表示，如图1（b）中的虚线部分，其中X、Y部分可以看成是IPMSM中B、C的延长线，这样与SPMSM类似，电压方程中不含有2θe项，进而可以依据SPMSM中滑模观测器的设计方法进行适用于IPMSM的滑模观测器的设计。

定义ee为扩展反电动势，且：

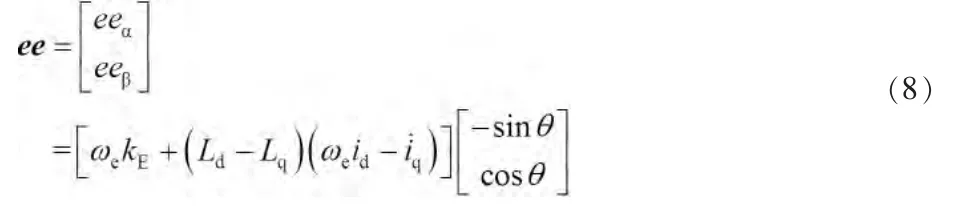
综上所述，将式（7）与式（8）称之为基于扩展反电动势模型的IPMSM电压方程。

2 基于EEMF模型的滑模观测器结构

根据式（7）与式（8），可以得到IPMSM以电流为状态变量的状态方程，如式（9）所示：

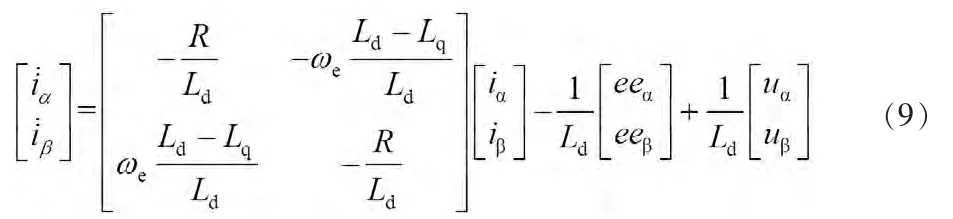
机定子两相静止坐标系下的电流分量作为状态变量，定义实际电流与重构电流偏差作为滑模切换面，选取饱和函数作为切换函数用以抑制抖动效应，将反电动势估计值作为反馈，引入到观测器电流模型中，构造如下形式滑模观测器：

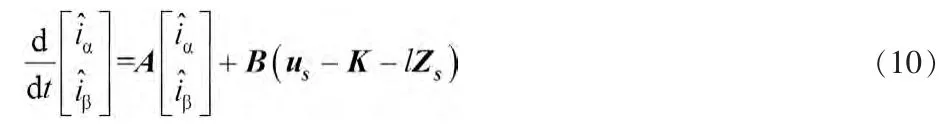
式中：

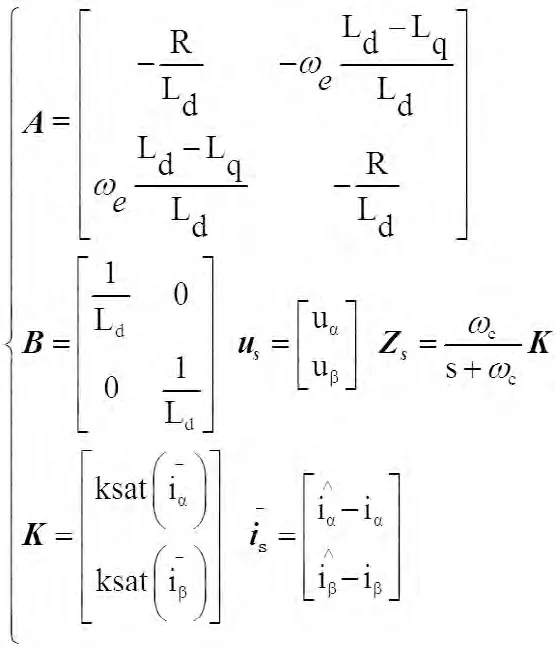
k为滑模增益，l为反馈系数，ωc为低通滤波器截止频率，sat(x)为饱和函数。

式（10）减式（9）可得电流估算误差方程为：

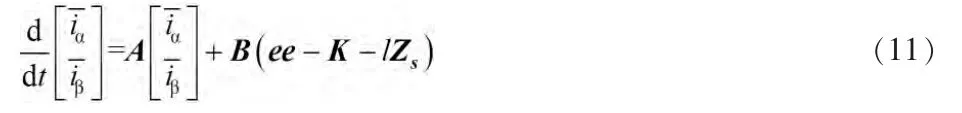
由于滑模切换面选择为s(is)=0，当系统状态空间轨迹运动到切换面上时，定子电流状态变量及其一阶导数均等于零即，将其代入式（11）可得：

转子位置可由下面方程估算出：

观测器中引入的用于滤除高频抖动分量的低通滤波器会造成信号相位的滞后，故需对估算的角度值进行补偿，补偿角度为：

式中：ωc为一常值，不同转速下相位补偿角度不同，需要存储大量值供查表实现。实际系统中采用截止频率可变的低通滤波器，其截止频率设为：

此时补偿角度为

上式为常值（μ为常数，通常取0.2～0.5）。

图2所示为基于扩展反电动势模型（EEMF）的滑模观测器结构示意图。

实际系统中滑模控制存在固有的抖振，故扩展反电动势估计值中也会含有高频抖动，直接利用三角函数计算转子位置会将抖动误差放大并引入到角度估计值中。锁相环电路对信号频率和相位的跟踪特性，能够提高角度和转速的提取精度。基于锁相环的角度与转速估计框图如图3所示。

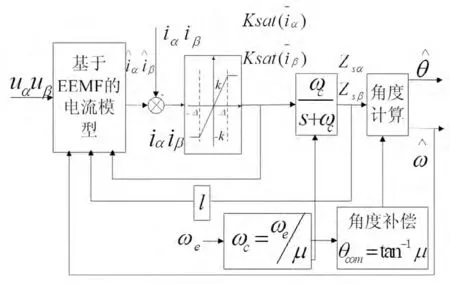
图2 基于EEMF模型的滑模观测器结构图

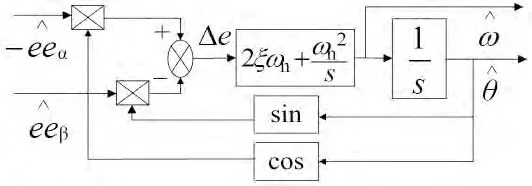
图3 基于锁相环的角度与转速估计框图

由图3可以得到：

当滑模运动产生时：

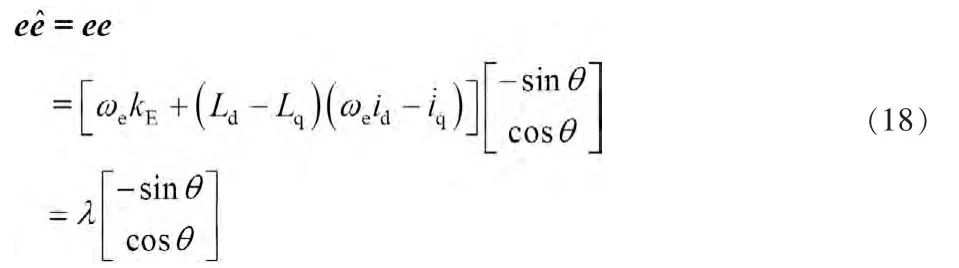
则式（17）可以化简为：

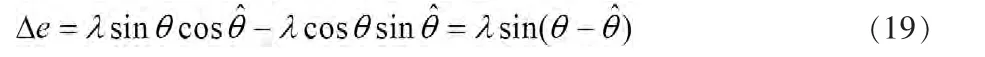
此时，基于锁相环的角度与转速估计框图可以等效为图4所示。由图4可以得到系统的闭环传递函数与位置估算的误差传递函数分别为式（21）、（22）所示。

图4 锁相环系统结构框图

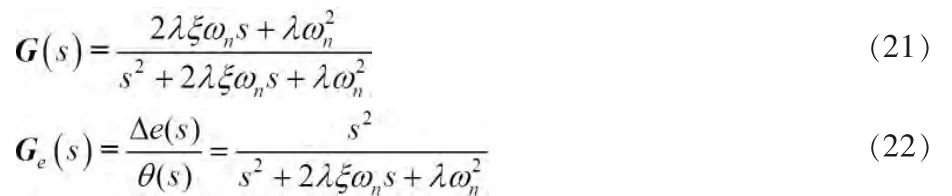
根据自动控制原理，系统的稳态误差为：

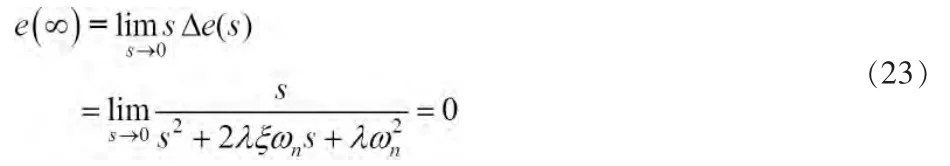
上式表明基于锁相环的角度与转速估计算法能够准确的从反电动势中提取出转子位置信息。

3 实验验证

为验证所设计滑模观测器的正确性，本文搭建了以TMS2812DSP为核心控制芯片的IPMSM无位置传感器矢量控制交流调速实验平台进行实验。实验中所用的内插式永磁同步电动机的详细参数如表1所示。

图5所示为转速为0.05Pu时，观测的反电动势波形。其中图（a）所示为采用传统滑模观测器得到的反电动势波形，图（b）所示为本文所设计的新型滑模观测器估计的反电动势波形，由图可以看出，新型滑模观测器由于引入了等效控制信号的反馈，提高了反电动势信息在开关信号中的比重，相比传统滑模观测器，得到的反电动势波形正弦度更高，抖动含量少。而且实验中可以发现，传统滑模观测器最低有效观测范围为0.05Pu，而本文设计的滑模观测器可以在0.01Pu下有效得到反电动势及转子位置信息，大大拓展了在低速段的工作范围。

表1 永磁同步电机参数

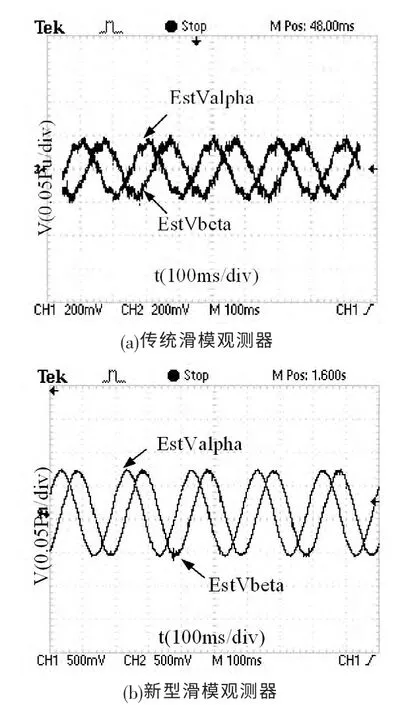
图5 反电动势观测波形

图6 （a）所示为转速0.05Pu时，新型滑模观测器所重构的电流波形，图6（b）所示为转速0.1Pu时，实测电流与重构电流波形。由图可知，随着转速的升高，重构电流的波形正弦度越好，验证了滑模观测器在高速时的性能优于低速。

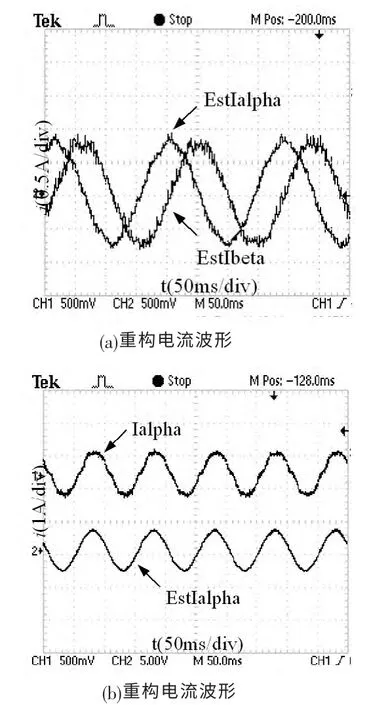
图6 观测器电流波形

另外，滑模观测器中重构电流所需要的定子相电压，并不是直接从电压传感器测量而来，因为绕组电压为一系列的开关脉冲含有大量谐波，而是采用空间矢量脉冲调制模块的给定参考电压，这样重构的电流并没有受到开关器件死区效应的影响，在图中可以看出重构的电流比实测电流波形更光滑。

4 结论

本文研究了滑模观测器用于内插式永磁同步电动机无位置传感器矢量控制系统中的一些关键问题，针对传统滑模观测器无法直接适用于IPMSM的情况，从数学模型上分析造成这种情况的原因，进而通过引入内插式永磁同步电机的扩展反电动势模型，设计适用于IPMSM的新型滑模观测器。最后通过实验验证了所提出新型滑模观测器的正确性和有效性。

［1］王成元,夏加宽,孙宜标.现代电机控制技术[M].北京：机械工业出版社,2008.

［2］叶金虎.现代无刷直流永磁电动机原理与设计[M].北京：科学出版社,2007.

［3］李华德.交流调速控制系统[M].北京：电子工业出版社,2003.