Irreversibility analysis of unsteady couette flow with variable viscosity*
EEGUNJOBI A. S., MAKINDE O. D., TSHEHLA M. S., FRANKS O.
1. Department of Mathematics and Statistics, Namibia University of Science and Technology, Windhoek,Namibia, E-mail: samdet1@yahoo.com 2. Faculty of Military Science, Stellenbosch University, Stellenbosch, South Africa 3. Faculty of Engineering Built Environment and Information Technology, Nelson Mandela Metropolitan University, Port Elizabeth, South Africa
Introduction
Study of flow and heat transfer in viscous incompressible fluids between two parallel plates, one of which is moving relative to the other, known as the Couette flow, is motivated by several important problems in engineering and industries[1]. Lichun and Duane[2]investigated the instabilities of a Couette flow composed of two layers of immiscible fluids experimentally and compared with the theoretical predictions of a linear instability analysis. Asghar and Ahmad[3]constructed the analytic solution for an unsteady Couette flow in the presence of an arbitrary non-uniform applied magnetic field. Makinde and Onyejekwe[4]reported a numerical solution for an MHD generalized Couette flow and heat transfer with variable viscosity and electrical conductivity. Since then, several authors have made interesting investigations of relatied flow and heat transfer in the Couette flow under various physical situations[5,6].
Meanwhile, the Couette flow and heat transfer processes are irreversible. This causes disorder in the flow system which can be quantified in term of entropy. Entropy generation analysis is closely associated with thermodynamic irreversibility and has become an important aspect of modeling and optimizing application in fluid flow and energy system for efficient operation. Bejan[7,8]presented a theoretical work on entropy generation in flow systems and heat transfer processes. The entropy generation in the Couette flow assisted with pressure gradient and four different combinations of thermal boundary conditions was reported by Aziz[9]. Makinde and Eegunjobi[10]considered theoretically the inherent irreversibility in a variable viscosity hydromagnetic generalized Couette flow with suction/injection at the walls. Butt et al.[11]studied entropy generation rate in hydrodynamic slip flow over a vertical plate with convective boundary.Some other papers such as[12-14]have also investigated entropy generation rate in flow system under various situations. From the literature survey, it seems that the problem of inherent irreversibility in an unsteady variable viscosity Couette flow has not received much attention.
In this paper, the combined effects of flow unsteadiness and temperature-dependent viscosity on entropy generation rate in a generalized Couette flow are investigated. In the following sections, the model problem is obtained and solved numerically using a semi-discretization finite difference method coupled with Runge-Kutta-Fehlberg integration scheme[15]. Pertinent results are presented graphically and discussed quantitatively.
1. Mathematical model
Consider the unsteady laminar flow of an incompressible variable viscosity fluid between two parallel plates channel under the combined action of a constant pressure gradient and uniform motion of the upper plate. It is assume that the channel width isa,the lower plate is fixed aty=0 while the uniform velocity of upper plate isUas depicted in Fig.1.
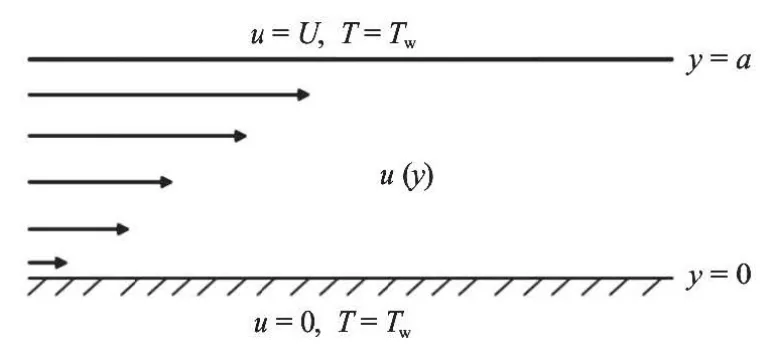
Fig.1 Schematic of the problem under consideration
Under the above assumptions, the governing equations for continuity, momentum and energy balance in one dimension can be written as[3-6,9]:
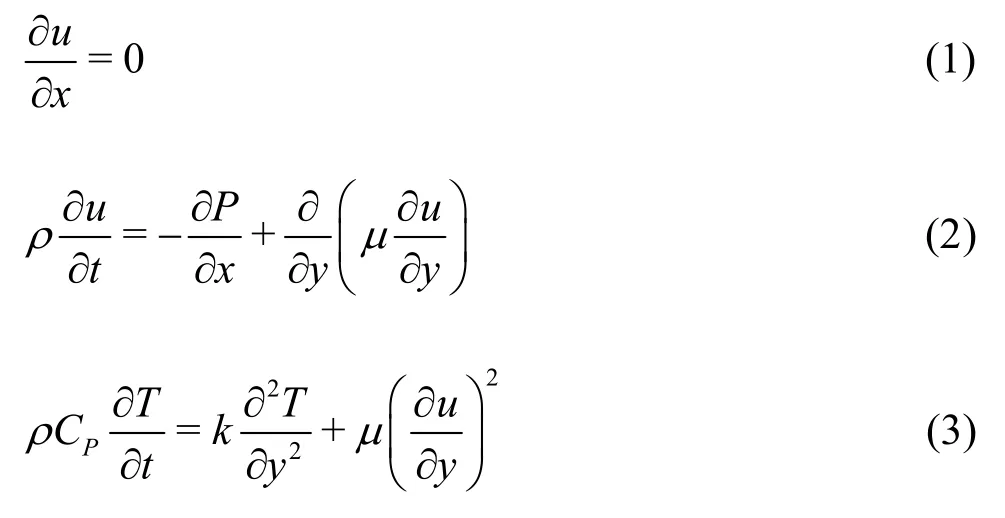
whereuis the axial velocity,μthe dynamic viscosity,ρthe fluid density,Tthe fluid temperature,Cpthe specific heat at constant pressure,kthe thermal conductivity of the fluid,Pthe fluid pressure andtthe time. The initial and boundary conditions are given as:
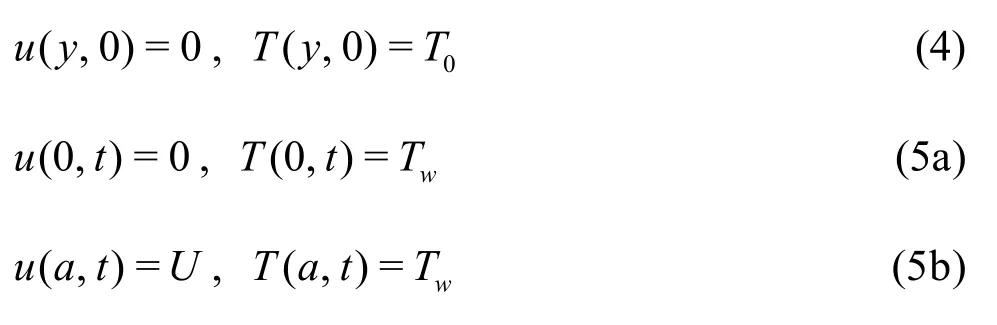
whereTwis the channel walls temperature andT0is the fluid initial temperature. The dynamical viscosityμis assumed to be an exponential decreasing function of temperature, given by

where0μis the initial fluid viscosity atT0andαis the variable viscosity parameter. We introduce the dimensionless variables as follows:
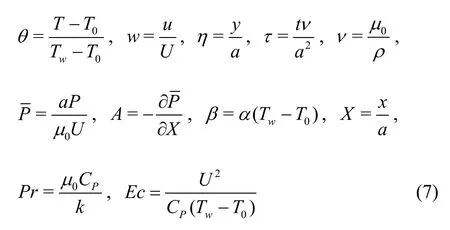
The dimensionless governing equations together with the appropriate initial and boundary conditions can be written as:
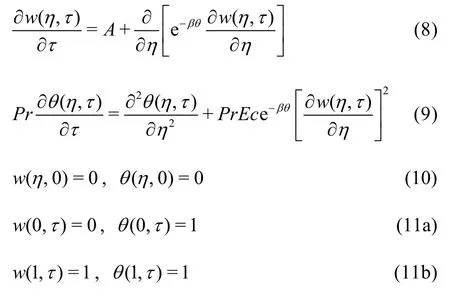
whereAis the pressure gradient,Ecthe Eckert number,Prthe Prandtl number, andβthe dimensionless viscosity variation parameter. The shear stress and the rate of heat transfer at the plate surface are given as:
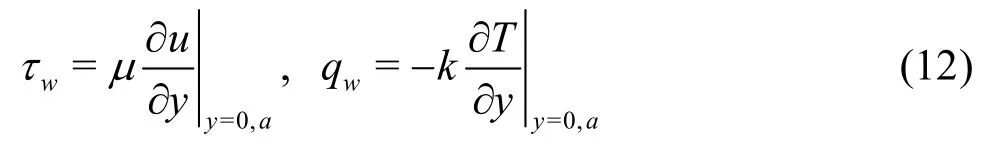
Using Eq.(12), the expression for skin-friction coefficient and the local Nusselt number are obtained:
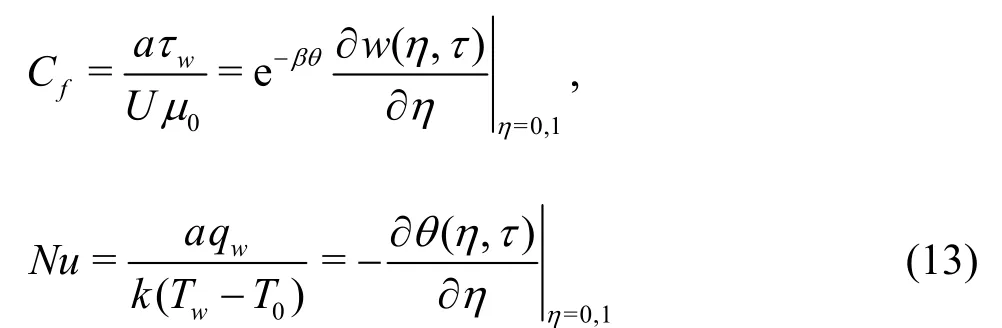
Equations (8)-(9) together with boundary conditions(10)-(11) constitute a coupled nonlinear boundaryvalue problem, which is solved numerically using a semi-discretization finite difference method together with the Runge-Kutta-Fehlberg integration scheme[15].Thereafter, the numerical results for the velocity and temperature profiles are obtained and utilized to compute the skin friction and the Nusselt number using the expression in Eq.(13).
2. Entropy analysis
Thermodynamic irreversibility and entropy generation are indispensable part of flow and heat transfer processes. Following Wood[12], the simplified volumetric rate of entropy generation is given by

where the first and the second terms on the right hand side of Eq.(14) are irreversibilities due to heat transfer and viscous dissipation respectively. Introducing the dimensionless quantities defined in Eq.(7) to Eq.(14)leads to
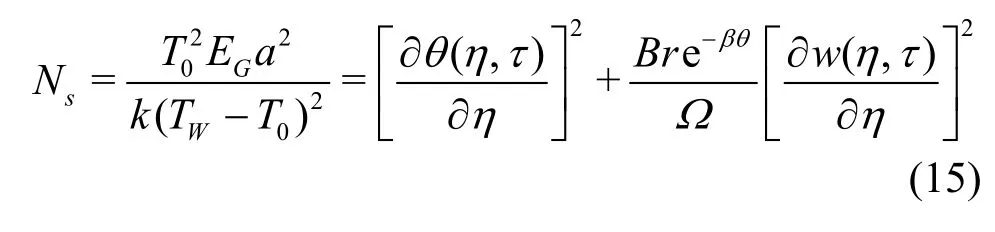

where

It is noteworthy thatBe=0 corresponds to the limit of dominant effects of fluid friction irreversibility whileBe=1 represent the heat transfer irreversibility dominant limit. WhenBe=1/2 both fluid friction and heat transfer contribute equally to the entropy generation in the flow process.
3. Results and discussion
Here, we have assigned numerical values to the parameters encountered in the problem in order to gain a clear insight into the entire flow structure and thermal development. Numerical solutions are displayed and discussed in Figs.2-22 below.
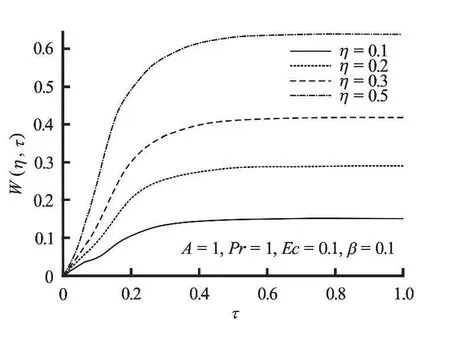
Fig.2 Velocity profiles with increasing space
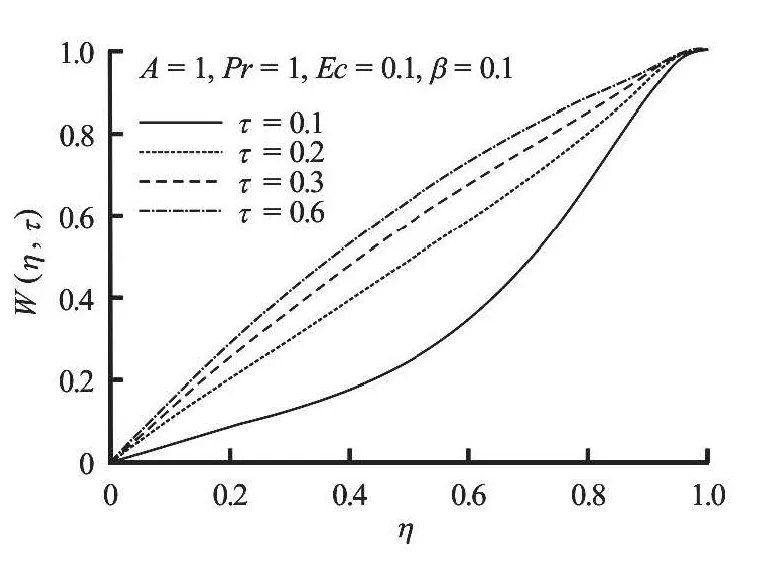
Fig.3 Velocity profiles with increasing time
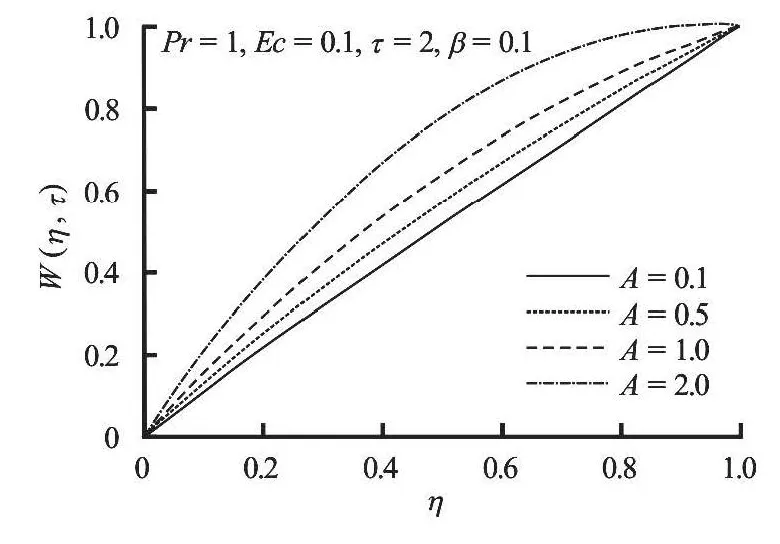
Fig.4 Velocity profiles with increasing A
3.1 Velocity profiles with parameter variation
Figures 2, 3 show that the fluid velocity increases gradually in time and space until it attains a steadystate atτ=0.8 for a given set of parameter values.Moreover, it is noteworthy that the fluid velocity is zero at the lower fixed plate and maximum at the upper moving plate satisfying the prescribed boundary conditions. The velocities in Figs.4 and 5 increase with the increase in pressure gradientAand dimensionless viscosity variation parameterβrespectively.This is expected, since as the values ofAandβincrease the fluid becomes lighter and flow faster due to a rise in temperature.

Fig.5 Velocity profiles with increasing β
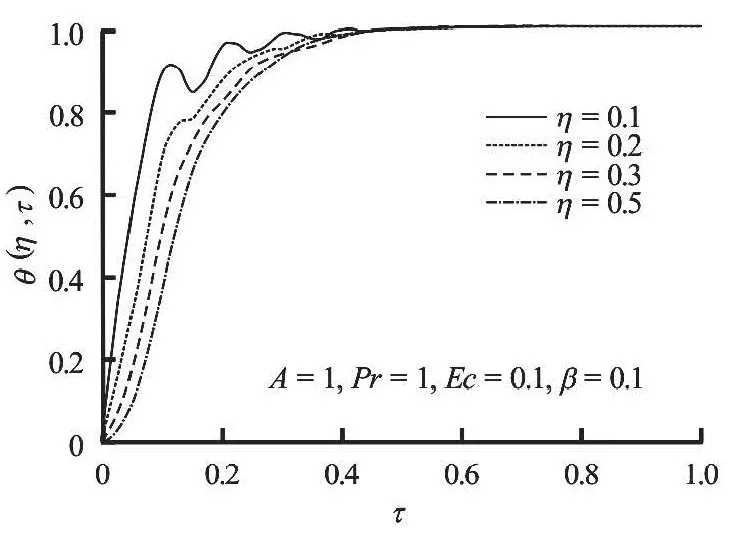
Fig.6 Temperature profiles with increasing space
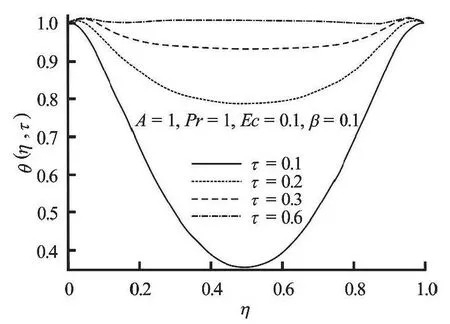
Fig.7 Temperature profiles with increasing time
3.2 Temperature profiles with parameter variation
Figures 6, 7 show that for a given set of parameter values, the fluid temperature increases both in space and time to its steady state valueτ=0.8. Interestingly, the fluid temperature is initially minimumwithin the channel centreline region, but increases gradually with time as the flow develops until steady state is achieved. Figure 8 depicts the effect of pressure gradient parameterAon the temperature profile.The increase inAraises the fluid temperature near the lower plate region and reduces the temperature near the moving upper plate region. In Fig.9 a generally decrease in the temperature across the flow is observed asβincreases. This may be attributed to the fact that the fluid viscosity decreases leading to a declination in the internal heat generation due to energy dissipation. Figures 10 and 11 show the effects of the Prandtl number,Prand the Eckert number,Econ the temperature. These figures show that as each of these parameters is increasing, the temperature profiles increases uniformly across the flow. This is expected, sinceEcandPrincrease, the internal heat generation increases due to a combined effect of viscous heating and decrease in thermal diffusivity.
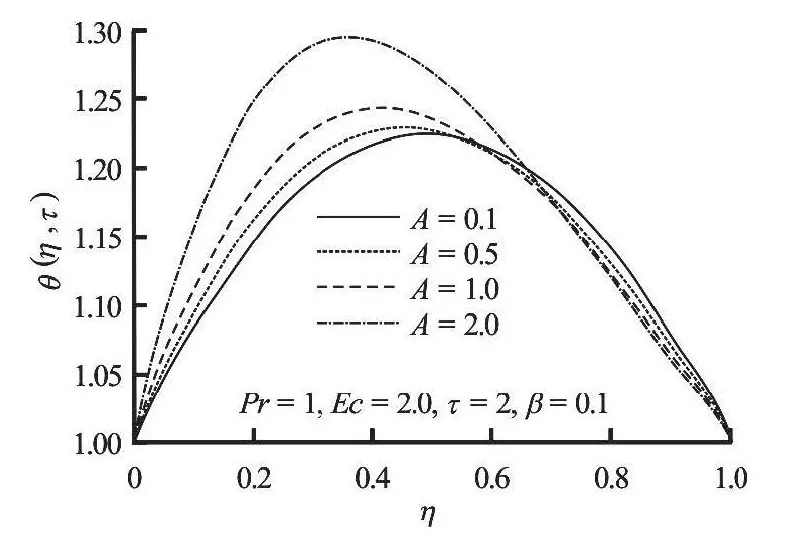
Fig.8 Temperature profiles with increasing A
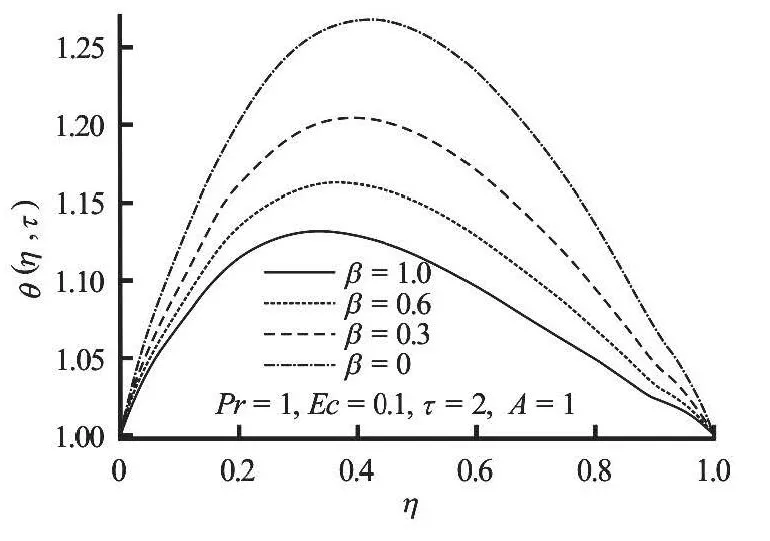
Fig.9 Temperature profiles with increasing β
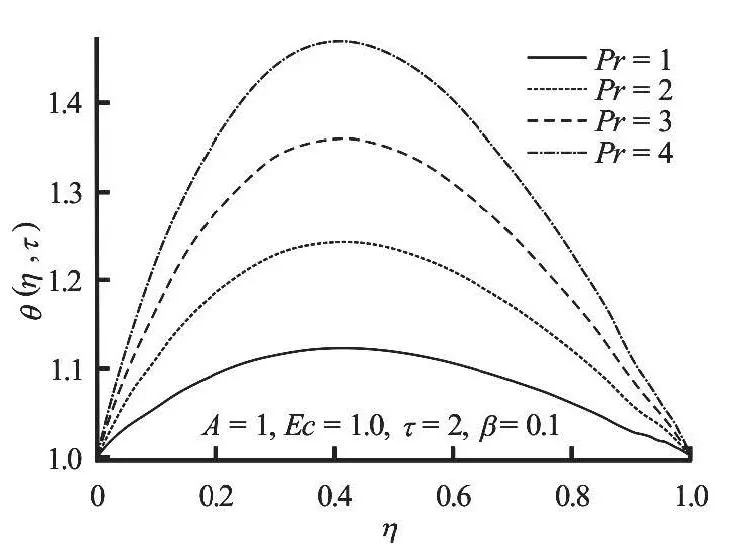
Fig.10 Temperature profiles with increasing Pr
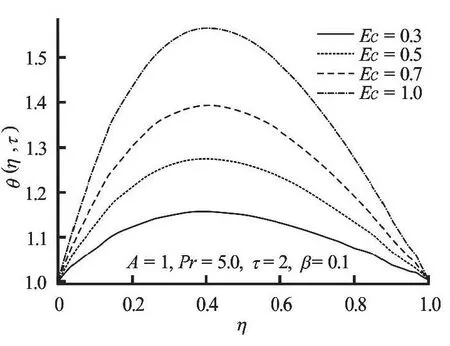
Fig.11 Temperature profiles with increasing Ec
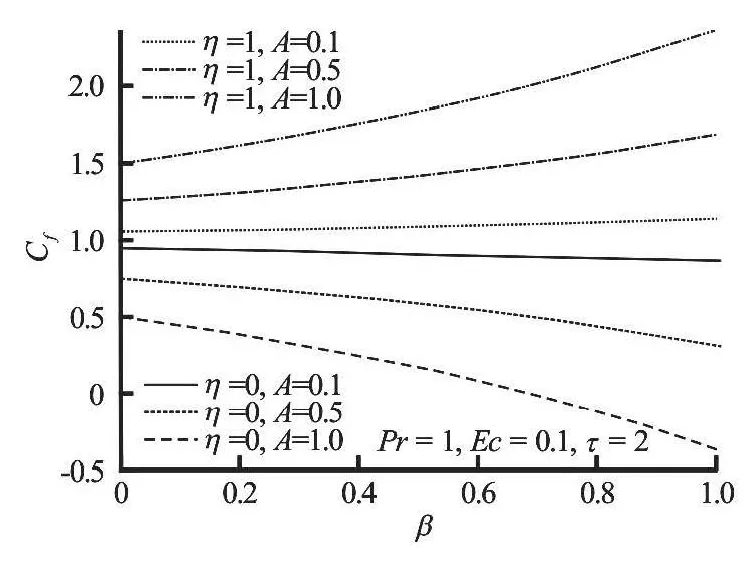
Fig.12 Variation of skin friction profiles with increasing A and β
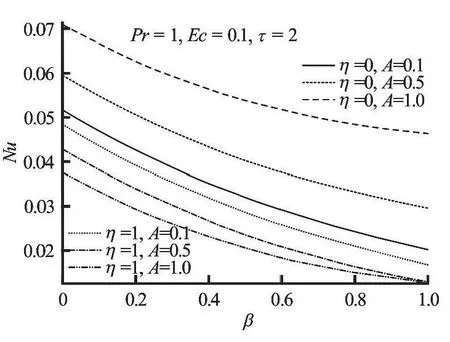
Fig.13 Variation of Nusselt number with increasing A and β
3.3 Skin friction and nusselt number with parameter variation
As the fluid viscosity decreases (i.e.,βincreases), the skin friction increases at the lower plate and decreases at the moving upper plate (see Fig.12). An increase in the pressure parameterAalso causes a further increase in the skin friction for the lower plate while the skin friction for the upper plate decreases.This is due to the fact that the fluid is lighter with high velocity gradient at the lower fixed plate and low velocity gradient at the moving upper plate. Figure 13 illustrates the effect of parameterAandβon the Nusselt number. The heat transfer rate at both lower and upper plates decreases with a decrease in the fluid viscosity. However, as the pressure gradient increases,an increase in the heat transfer rate at the lower plate is observed while the Nusselt number at the moving upper plate decreases. Figure 14 shows that the Nusselt number increases with increasing values ofEcandPr. This may be attributed to a rise in the temperature gradient at both upper and lower plates due to viscous heating.
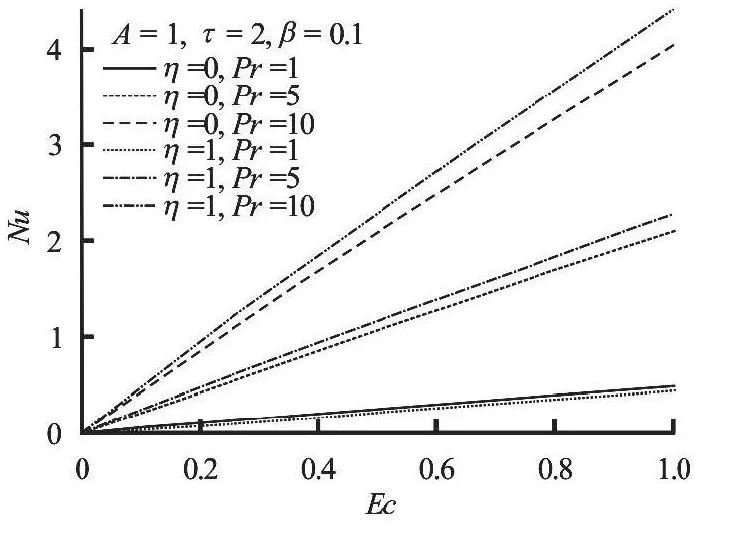
Fig.14 Variation of Nusselt number with increasing Pr and Ec
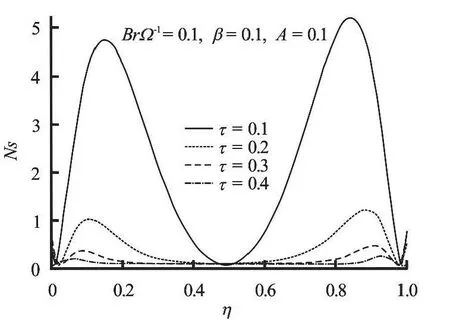
Fig.15 Variation of entropy generation rate with increasing time
3.4 Entropy generation rate with parameter variation
The entropy production near the fixed lower plate and the moving upper plate suddenly increases and gradually decreases in time until the steady state is achieved as shown in Fig.15. It is noteworthy that the channel centreline region (η= 0.5) is not affected by the entropy production at the flow development state.When the flow is hydrodynamically and thermally developed into a steady state, a decrease in entropy generation across the channel is noticed with maximum entropy production at the fixed lower plate and minimum at the moving upper plate as illustrated inFigs.16-18. However, the entropy production declines as the fluid viscosity decreases (i.e.,βincreases).Figure 17 shows that the entropy generation rate increases with an increase in the value of parameter groupdue to viscous dissipation effect. In Fig.18, the entropy generation rate near fixed lower plate increases while it decreases near the moving upper plate as the pressure gradient increases. Interestingly, the entropy generation rate along the channel centreline region is not affected with increasing parameter value ofA.
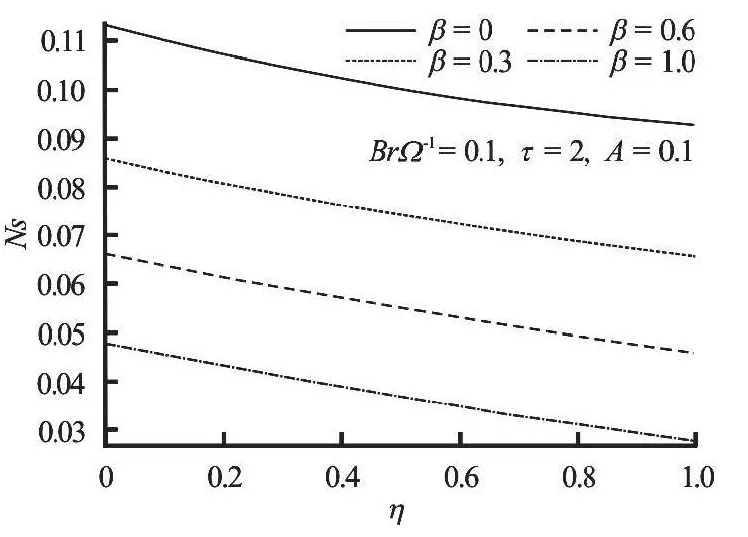
Fig.16 Variation of entropy generation rate with increasing β

Fig17 Variation of entropy generation rate with increasingBrΩ-1
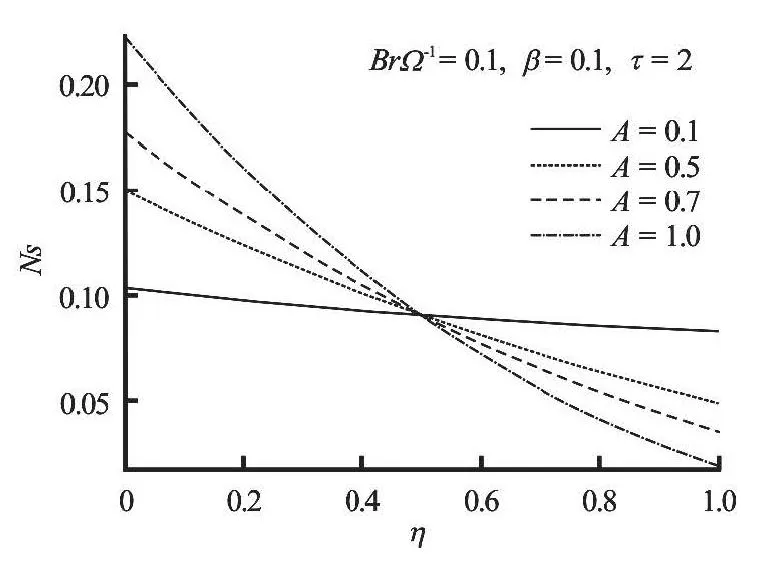
Fig.18 Variation of entropy generation rate with increasing A
3.5 Bejan number with parameter variation
The Bejan number suddenly increases and then gradually decreases near both the lower and upper plate region as time increases until the steady state flow condition is achieved as illustrated in Fig.19.This implies that the sudden dominant effect of heat transfer irreversibility diminished in time and the dominant effect of fluid friction gradually takes over until the flow becomes steady. Meanwhile, it is interesting to note that the fluid friction irreversibility dominate along the channel centerline region. For hydrodynamically and thermally developed flow at steady state, the dominant effects of heat transfer irreversibility is observed near both the fixed lower plate and the moving upper plate region while the fluid friction irreversibility dominate the entropy production along the channel centreline region as shown in Figs.20-22.Moreover, the Bejan number decreases near the lower plate and increases near the upper plate as the parameter value ofAincreases (see Fig.20). This implies that the dominant effect of heat transfer irreversibility decreases at lower plate and increases at the upper plate as the pressure gradient parameter increases.Figure 21 shows that the dominant effect of irreversibility due to heat transfer is enhanced near both lower and upper plate regions as the parameter groupincreases. A decrease in fluid viscosity enhances the dominant effects of entropy generation due to viscous dissipation at both plates as shown in Fig.21.
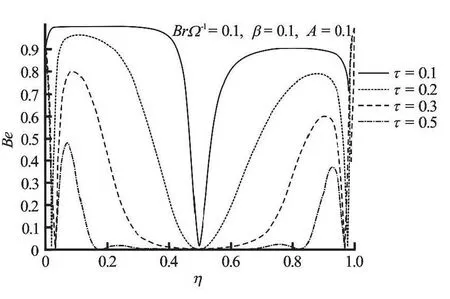
Fig.19 Variation of Bejan number with increasing time
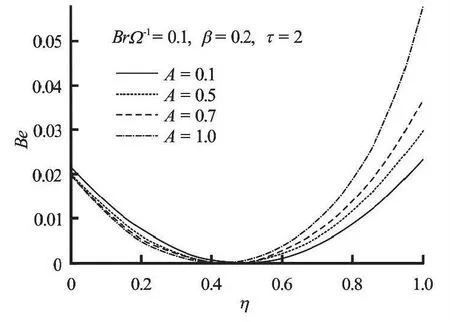
Fig.20 Variation of Bejan number with increasing A
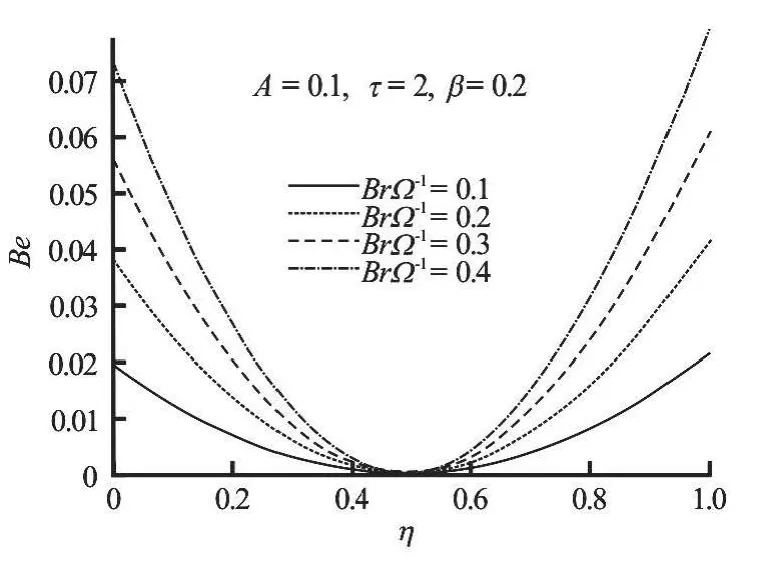
Fig.21 Variation of Bejan number with increasing BrΩ-1
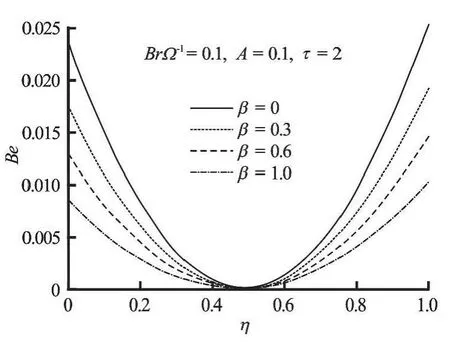
Fig.22 Variation of Bejan number with increasing β
4. Conclusions
The inherent irreversibility in an unsteady variable viscosity Couette flow has been numerically investigated. The governing equations are solved using a semi-discretization finite difference method coupled with Runge-Kutta-Fehlberg integration schem.The results obtained can be summarized as follows:
(1) For a given set of parameter values, the velocity and temperature increase unsteadily until steady flow condition is achieved. Futher increase is observed with increasing values ofAandβ.
(2) Fluid temperature increases with increasingPr,EcandA, but decreases with increasingβ.
(3) The skin friction increases at the fixed lower plate and decreases at the moving upper plate withβandA.
(4) Increase inβcauses the decrease inNswhile increase inBrΩ-1leads to the increase inNs.The entropy generation rate increases at lower plate and decreases at upper plate asAincreases.
(5) Fluid friction irreversibility dominates the channel centreline region. The increase inβcauses the increase inBewhile the increase inBrΩ-1causes the decrease inBenear the lower and upper plate regions.
[1] WHITE F. S. Viscous fluid flow[M]. New York, USA:McGraw-Hill, 1974.
[2] LICHUN D., DUANE J. Experimental and theoretical study of the interfacial instability between two shear fluids in a channel Couette flow[J]. International Journal of Heat and Fluid Flow, 2005, 26(1): 133-140.
[3] ASGHAR S., AHMAD A. Unsteady Couette flow of viscous fluid under a non-uniform magnetic field[J].Applied Mathematics Letters, 2012, 25(11): 1953-1958.
[4] MAKINDE O. D., ONYEJEKWE O. O. A numerical study of MHD generalized Couette flow and heat transfer with variable viscosity and electrical conductivity[J]. Journal of Magnetism and Magnetic Materials,2011, 323(22): 2757-2763.
[5] CHINYOKA T., MAKINDE O. D. Analysis of transient generalized Couette flow of a reactive variable viscosity third-grade liquid with asymmetric convective cooling[J]. Mathematical and Computer Modelling,2011, 54: 160-174.
[6] ATTIA H. A., KOTB N. A. MHD flow between parallel plates with heat transfer[J]. Acta Mechanica, 1996, 117:215-220.
[7] BEJAN A. Second-law analysis in heat transfer and thermal design[J]. Advances in Heat Transfer, 1982, 15:1- 58.
[8] BEJAN A. Entropy oeneration minimization[M].Boca Raton, USA: CRC Press, 1996.
[9] AZIZ A. Entropy generation in pressure gradient assisted Couette flow with different thermal boundary conditions[J]. Entropy, 2006, 8(2): 50-62.
[10] MAKINDE O. D., EEGUNJOBI A. S. Analysis of inherent irreversibility in a variable viscosity MHD generalized Couette flow with permeable walls[J]. Journal of Thermal Science and Technology, 2013, 8(1): 240-254.
[11] BUTT A. S., MUNAWAR S. and ALI A. et al. Entropy generation in hydrodynamic slip flow over a vertical plate with convective boundary[J]. Journal of Mechanical Science Technology, 2012, 26(9): 2977-2984.
[12] WOOD L. C. Thermodynamics of fluid systems[M].Oxford, UK: Oxford University Press, 1975.
[13] MAKINDE O. D. Thermodynamic second law analysis for a gravity-driven variable viscosity liquid film along an inclined heated plate with convective cooling[J].Journal of Mechanical Science and Technology, 2010,24(4): 899-908.
[14] CHAUHAN D. S., KUMAR V. Heat transfer and entropy generation during compressible fluid flow in a channel partially filled with porous medium[J]. International Journal of Energy Technology, 2011, 3(14): 1-10.
[15] NA T. Y. Computational methods in engineering boundary value problems[M]. New York, USA: Academic Press, 1979.
- 水动力学研究与进展 B辑的其它文章
- Erratum to “Estimation of drag forces caused by natural woody vegetation of different scales”
- The effect of a curved bed on the discharge equation in a spillway with a breast wall*
- Three-dimensional simulation for problem of penetrative convection near the maximum density*
- Effect of vegetation on flow structure and dispersion in strongly curved channels*
- Numerical investigation of the concentric annulus flow around a cylindrical body with contrasted effecting factors*
- Thermodynamic analysis for a third grade fluid through a vertical channel with internal heat generation*

