基于配置积分器的GPS卫星精密星历轨道拟合

闫志闯，徐君毅，李 岩，余春平

1. 信息工程大学，河南 郑州，450001；2.测绘信息技术总站，陕西 西安，710054；3.第一测绘导航基地， 辽宁 大连，116031



基于配置积分器的GPS卫星精密星历轨道拟合

闫志闯1,2，徐君毅2，李 岩3，余春平2

1. 信息工程大学，河南 郑州，450001；2.测绘信息技术总站，陕西 西安，710054；3.第一测绘导航基地， 辽宁 大连，116031

本文详细推导了配置积分器的基本原理，并针对卫星进入地影或月影时配置积分器需要变步长的问题，提出了将变步长配置积分器转换为定步长的改进方法；同时，利用CODE精密星历作为虚拟观测量，进行轨道拟合实验。实验结果表明：与GPS精密星历相比，拟合后的轨道在R、T和N三个方向RMS均在0.01m以内。

配置积分器；轨道拟合；轨道确定；全球定位系统

1 引 言

卫星定轨中需要求解三个微分方程，即：运动微分方程、状态转移矩阵微分方程和敏感矩阵微分方程[1]。若通过解析法直接求得三个常微分方程解的显式表达式，通常很困难甚至不可能。因此多采用数值解法，采用RK积分器、RKF积分器等单步积分器，也有Adams、Cowell等多步积分器。此外，还有配置积分法，该方法已经成功应用于国外Bernese软件中[2]。文献[3]分析了不同步长和积分器阶数对积分的影响，得出采用积分步长为1小时、10阶多项式的配置积分器进行GPS精密星历轨道拟合是合适的；文献[4]比较了其他积分器和配置积分器在轨道拟合中的差别，指出了配置积分器自身的优势。此外，配置积分器还应用于低轨卫星定轨和重力场恢复、导航卫星精密定轨中[5-9]。本文基于自主开发的卫星精密定轨定位软件对CODE提供的SP3精密星历进行轨道拟合，得到了较好的结果；同时，提出了将变步长配置积分器转换为定步长的改进算法。

2 配置积分器

2.1 基本原理

配置积分器的核心思想是：在一个不是很长的积分区间[ak,ak+1)，k=0,1,2…表示积分区间编号，将卫星的位置、状态转移矩阵和敏感矩阵在边界ak处用q次多项式泰勒展开；核心问题是：要已知卫星位置速度、状态转移矩阵和敏感矩阵在ak点处的直到q次导数(q从0开始计数)。此时，卫星在区间[ak,ak+1)内任意时刻的位置速度、状态转移矩阵和敏感矩阵可以由该泰勒多项式表示。

假设时间区间[ak,ak+1)内时刻t处的状态量z(t)在初始a时刻q次泰勒展开为：

(1)

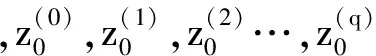
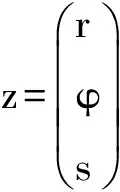
(2)

其中，r表示卫星的位置，φ和s为压缩成列向量后的状态转移矩阵和敏感矩阵。为了形式需要，下文对其按照矩阵形式，根据文献[9]以及文献[1]中对三个微分方程的定义， 直接给出三个二

阶微分方程：

(3)

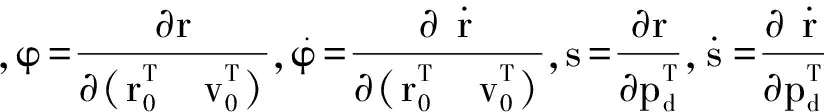
令ak=a，ak+1=b，将该区间平均分为q-2段共q-1个节点，区间中的节点分别为ti，则有

(4)

对式(1)方程两边求2次导数，则得到:

(5)

动态生成的落脚点在于生成性。但它不是自然而然就能实现的，而是要通过一定的方法和实践过程。过程哲学观代表人物怀特海认为，“世界事物分为事件的世界和永恒客体的世界。事件世界中的一切都处于变化的过程之中，过程就是机体各个因子之间有内在联系的、持续的创造活动，它表现为机体可以转化为另一机体，因而整个世界就表现为一种活动的过程” [2]。但这个生成的过程和效果是由教师和学生的互动来决定的，而且要采取多元化的策略。如果互动形式过于单一，譬如缺乏层次性和深度、互动内容过少等，则难以收到良好的效果。

(6)

将第0到第q-2共q-1个节点按照式(6)写成矩阵形式为：

(7)

(8)

则可以得到初始时刻状态量z的从2阶到q阶导数构成的矩阵为：

(9)

式(9)中的任意第i列对应初始时刻状态量z的i阶导数，加上式(3)中三个微分方程的初值作为状态量z的零阶导和一阶导数，最终可以得到式(1)中的初始时刻状态量z从0阶直到q阶导数；然后通过式(1)得到第0到q-2节点的状态量，进行迭代计算。通常需要迭代多次才能达到理想效果，迭代终止条件为tq-2节点处的卫星位置前后两次差值小于某一指定数值，该值通常取0.01m即可。

2.2 配置积分器的起步

2.3 算法改进与实现

(10)

实际相当于对式(1)中的系数采用以步长b-a作为单位。因此，采用归一化时间作为单位和非归一化时间作为单位时，式(1)中的泰勒系数之间的关系为：

(11)

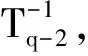
3 数据实验与结果分析

为了验证配置积分器的积分效果，采用2010年年积日为4～13共10天的CODE精密星历作为虚拟观察量，动力学模型如表1所示。其中，积分器步长设置为1小时，多项式阶数设定为10阶，最大迭代次数设置为3次。选取GPS02和GPS03星拟合结果，在RTN三方向与CODE精密星历比较，RTN三方向残差如图1和图2所示，RMS三方向残差如图3和图4所示。

表1 GPS轨道拟合动力学模型

地球引力场模型潮汐模型光压模型相对论效应摄动12×12EGM2008模型固体潮，海潮，极潮，固体极潮，海洋极潮，采用IERS2010推荐模型9参数太阳光压模型IERS2010推荐模型

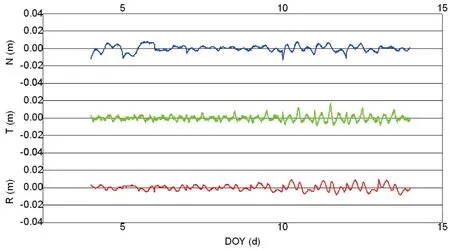
图1 GPS02星RTN三方向残差

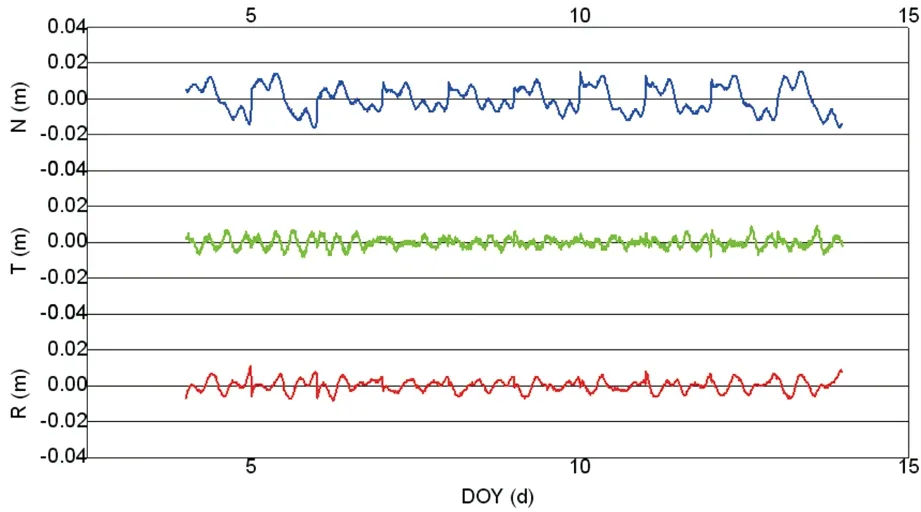
图2 GPS03星RTN三方向残差

图3 GPS02星RTN三方向RMS

图4 GPS03星RTN三方向RMS

由以上结果可知：

(1)由图1、图2可以看出， GPS02星在R、T、N三方向残差都在厘米级，除了T和N方向极个别历元外，均不超过0.01m；GPS03星在R和N方向残差不超过0.01m，在N方向残差不超过0.02m；整体上看，两颗星三个方向残差均不超过0.02m。

(2)由图3、图4可以看出，两颗星10天的拟合精度均比较稳定，GPS02星T方向RMS最大为0.007m，R和N方向均在0.005m以内；GPS03星N方向RMS稍差，在第5天和第13天接近0.01m，R和T方向较好，均不超过0.05m；整体上看，两颗星三个方向RMS均不超过0.01m。

(3)综合以上分析可以看出，配置积分器用于GPS卫星精密星历拟合，可以实现相对原精密星历毫米级精度的连续轨道，并且该轨道可以用于事后GPS精密定位和星载GPS低轨卫星精密定轨中。

4 结 论

与传统的积分器相比，利用配置积分法对GPS轨道进行数值积分时由于积分步长较大，因此所需的计算时间较少。然而，当卫星进入地影或月影时，卫星受力不连续，需要精确计算卫星进出地影的时间，最终导致上述积分区间不是等步长，产生变步长问题。采用本文提出的改进方法，可以将变步长问题转换为定步长问题，在简化编程实现、提高计算效率的同时，保证了轨道拟合的精度。因此，本文提出的配置积分器改进方法在卫星定轨中具有一定的应用价值。

[1]闫志闯, 张传定, 杜兰等. 基于面向对象的卫星轨道确定优化方法研究 [J]. 大地测量与地球动力学, 2013, 33(2): 96-100.

[2]DACH R, HUGENTOBLER U, FRIDEZ P, et al. Bernese GPS Software Version 5.0 [M]. Bern: Astronomical Institute, University of Bern, 2007.

[3]李征航, 龚晓颖, 刘万科. 配置法在卫星轨道积分中的应用 [J]. 武汉大学学报(信息科学版), 2010, 35(3): 253-256.

[4]常志巧, 郝金明, 张成军. 配置积分方法在GPS卫星轨道确定中的应用 [J]. 海洋测绘, 2006, 26(2): 31-33.

[5]BEUTLER G, J GGI A, MERVART L, et al. The celestial mechanics approach: application to data of the GRACE mission [J]. Journal of Geodesy, 2010, 84(11): 661-81.

[6]BEUTLER G, BROCKMANN E, HUGENTOBLER U, et al. Combining consecutive short arcs into long arcs for precise and efficient GPS Orbit Determination [J]. Journal of Geodesy, 1996, 70(5): 287-99.

[7]BEUTLER G, J GGI A, HUGENTOBLER U, et al. Efficient satellite orbit modelling using pseudo-stochastic parameters [J]. Journal of Geodesy, 2006, 80(7): 353-72.

[8]BEUTLER G, J GGI A, MERVART L, et al. The celestial mechanics approach: theoretical foundations [J]. Journal of Geodesy, 2010, 84(10): 605-24.

[9]BEUTLER G. Methods of Celestial Mechanics Volume 1: Physical, Mathematical, and Numerical Principles [M]. New York: Springer-Verlag, 2005.

GPS Satellite Precise Ephemeris Orbit Fitting Based on Collocation Integration

Yan Zhichuang1,2，Xu Junyi2, Li Yan3, Yu Chunping2

1. Information Engineering University, Zhengzhou 450001, China 2.Technical Division of Surveying and Mapping, Xi’an 710054, China 3.The First Surveying, Mapping & Navigation Base Dalian 116031, China

This paper deduces the principle of collocation integration in detail. In view of the variable step problem caused by earth or moon shadow, the paper proposes an optimum method based on matrix operation to improve the efficiency. The precise ephemeris of CODE is used as the virtual measurement to fit the orbit. The experiments results show that the RMS in the R, T and N direction is less than 0.01m compared to the GPS precise ephemeris.

collocation integration; orbit fitting; orbit determination; GPS

2015-03-30。

国家自然科学基金资助项目(41104047；41174026)。

闫志闯(1982—)，男,博士研究生，主要从事卫星大地测量与导航方面的研究。

P237；TP751.1

A