The Study of Thermal Stresses of a Two Phase FGM Hollow Sphere

Baoyu Ma, Guansuo Dui, Shengyou Yang and Libiao Xin

1 Introduction

Functionally graded materials(FGMs)are composite materials formed of two or more constituent phases with a continuously variable composition.FGMs have a lot of advantages that make them attractive in potential applications,including a potential reduction of in-plane and transverse through-the-thickness stresses,an improved residual stress distribution,enhanced thermal properties,higher fracture toughness,and reduced stress intensity factors.To aid in the design of FGM,it would be useful to havea clear underst anding of the manner in which the property gradients affect the induced thermal stresses.

Many researchers studied the thermal stresses in FGM structures by using numerical methods.Fukuietal.(1993)presented a numerical solution for the problem of uniform heating of a radially inhomogeneous thick-walled cylinder.Alavietal.(1993)and Kwon et al.(1994)investigated the mechanical behavior of a gradient sphere under inhomogeneous temperature distribution.Wang and Mai(2005)used the finite element method to analyze the transient heat conduction of onedimensionalproblems. By the MLPG method, Sladek et al. (2008a, b, c, 2009) discussedsome thermoelastic problems of FGM structures, including thermal bendingand transient heat conduction. Dong L et al. (2012, 2013a, b) developed a usefuland reliable procedure of stochastic computation, which was combined with thehighly accurate and efficient Trefftz Computational Grains, for a direct numericalsimulation of heterogeneous materials with microscopic randomness. It can be usedfor ground-breaking studies in micromechanical modeling of composite materials.Analytical solutions of the thermal problems in FGM structures are presented inmany previous papers. Sugano (1990) gave the analytical solutions for the thermalstresses in a hollow cylinder whose Young’s modulus and coefficient of thermalexpansion radially varied but with a constant Poisson ratio. Lutz and Zimmerman(1996, 1999) presented the solution for the problem of uniform heating of a sphereand a cylinder whose elastic modulus and coefficient of thermal expansion linearlyvary in the radial direction.

Using perturbation techniques, Obata and Noda (1994) studied the thermal stressesin a FGM hollow sphere and cylinder with uniform temperature. In termsof the Green’s function approach, Kim and Noda (2002a, b) discussed the twodimensionalunsteady thermoelastic problem of a FGM infinitely long hollow cylinder.With the assumption that the nonhomogeneous material properties vary in thethickness direction, Jeon et al. (1997) solved the thermal stresses for a slab and asemi-infinite body, while Nadeau and Ferrari (1999) presented a one-dimensionalthermal stress analysis of a transversely isotropic layer.

Assuming that the material properties are expressed as power functions of radius,analytical solutions of the Navier equations are presented in the following papers.Jabbari et al. (2002, 2003) derived analytical solutions for one-dimensional and twodimensional steady-state thermoelastic problems of the functionally graded circularhollow cylinder. Considering mutual effect of thermal and mechanical loads, Eslamiet al. (2005), Jabbari et al. (2008), Poultangaria et al. (2008), Sadeghian andToussi (2011) analytically solved the governing equation mechanical and thermalstresses in the FGM structures respectively.

As discussed above, the thermal and mechanical properties of the structures areassumed as special functions (such as power functions) of the radius or thicknessdue to their mathematical limitations. This assumption makes it possible to obtainthe analytical solutions of the Navier equations. Actually, FGMs are compositematerials in which the concentrations of the various phases are controlled so as tocreate gradients in macroscopic physical properties such as elastic moduli, thermalconductivity and thermal expansivity. In other words, the properties gradients ofFGM only depend on the ways to change the composition, hence we can studythe FGM structures by the volumetric ratio of constituents instead of assum ing the material properties functions.

In this paper,westudy the problem of the uniform heating of a FGM hollow sphere made of two phases of different materials,and both of whose volume fractions vary radially.Based on the Voigt constant strain approximation,we present the analytical solution for the stresses,displacements and the effective coefficient of thermal expansion within the hollow sphere.

2 Theoretical model

2.1 Governing equations for radially symmetric deformations

Considera thick hollow FGM sphere of inner radiusaand outer radiusb.The FGM is a two-phase composite material.The two components,denoted by material A and material B,whose volume fractions vary in ther-direction,thus the material properties are functions ofr.Letube the radial displacement.It is assumed that the volume fraction of material B is the function ofras

For small deformation,the strain-displacement relations are

With the Voigt constant strain approximation,we have

The average stress is:

Wherei=0,1 demotes material A and B,respectively;σklandεkl(k,l=r,θ)are the average stress and strain tensors,respectively;σiaverage stress and strain tensors of thei-thmaterial,respectively.

The thermoelastic stress-strain relations for an isotropic material are

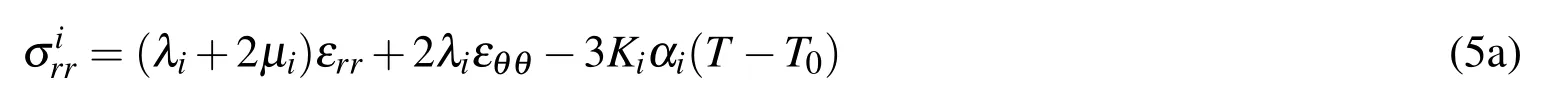
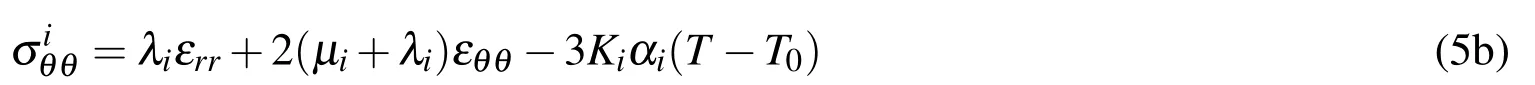
whereλandµare the Lamé parameters,respectively,αis the coefficient of thermal expansion,Kis the bulk modulus,Tis the temperature andT0is the reference temperature at which the sphere is stress-free.

The equilibrium equation is

Combining Eqs.(2)-(5),the average stress-displacement relations are:

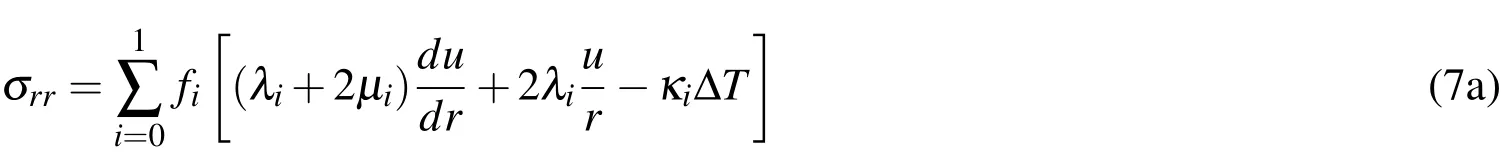
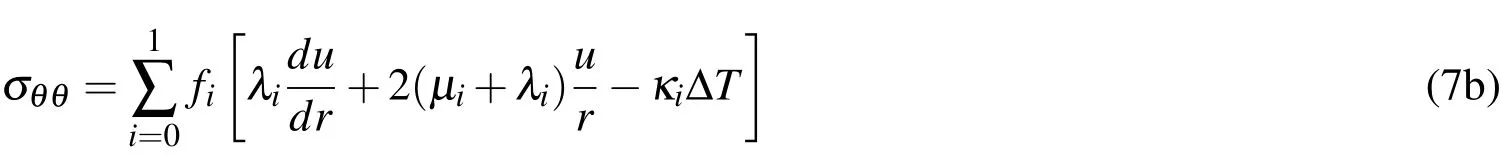
whereκi=3Kiαi=(3λi+2µi)αi,ΔT=(T-T0).

Substituting Eqs.(7)and(1)into the stress equilibrium equation(6),we have the following governing equation:

where

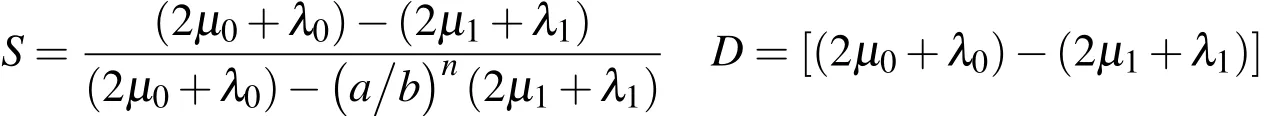
Using the transformationsu=ry(z)and,Eq.(8),a hypergeometric differential equation,reduces to

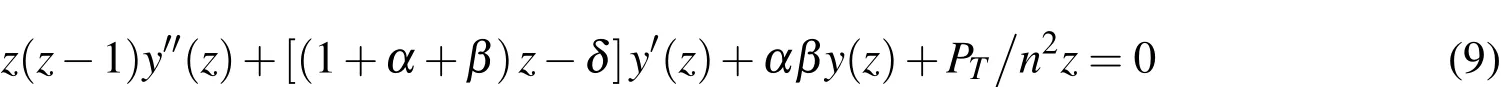
where

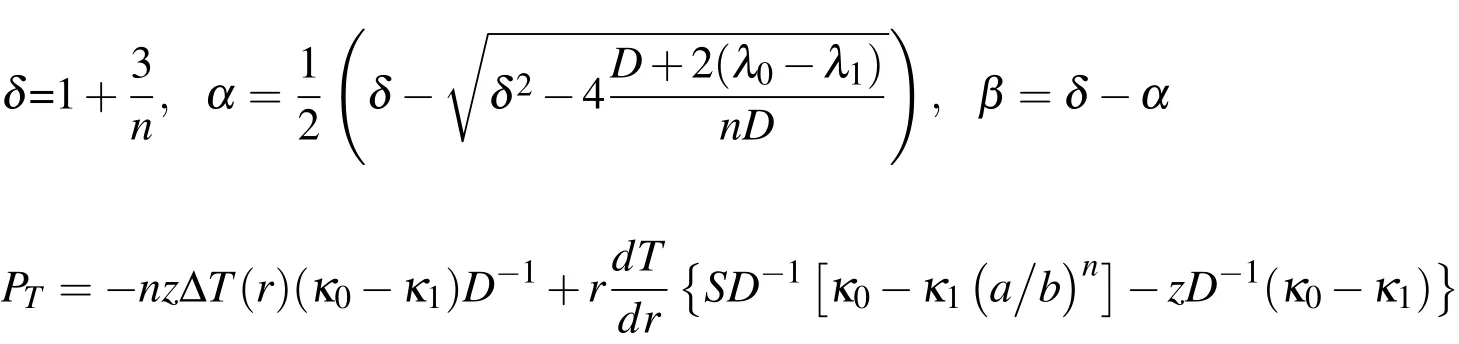
2.2 Thermal stresses of a FGM spherical shell

Now consider the thermal stresses in a hollow sphere that is uniformly heated.In this case,inPTof Eq.(9)vanishes and Eq.(9)becomes:

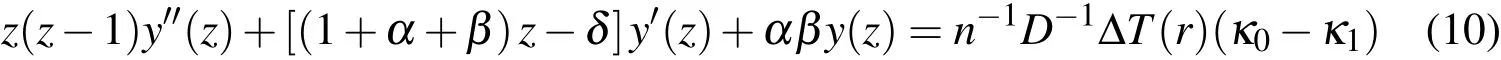
The solution of Eq.(10)is

whereC1andC2are integral con stants andFis the hypergeo metric function defined for

Here(q)mis the Pochhammer symbol,which is defined by

Recall the transformationu=ry(z),the radial displacement is finally given by

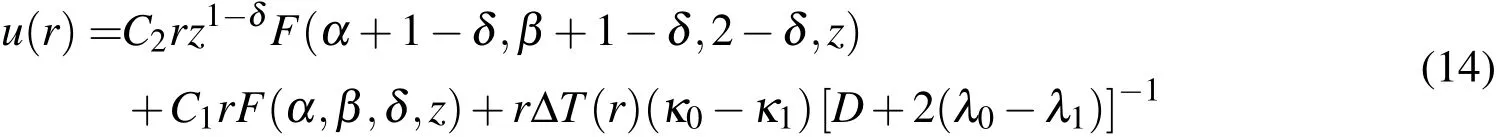
Substituting Eq.(14)into Eqs.(2)and(7),the strains and stresses can be obtained.The integral constantsC1andC2can be determined by the boundary conditions.

2.3 Convergence of the series solution

It is obvious that the hyper geometric series converges for0≤z≤1,however,this is not true forz＜0 orz＞1.To insure the convergence of the hyper geometric seriesFin Eq.(11)on the intervala≤r≤b,the following variable transformations can be used to convert Eq.(10)into another hypergeo metric differential equation ofwith the independent variable∈[0,1]as:

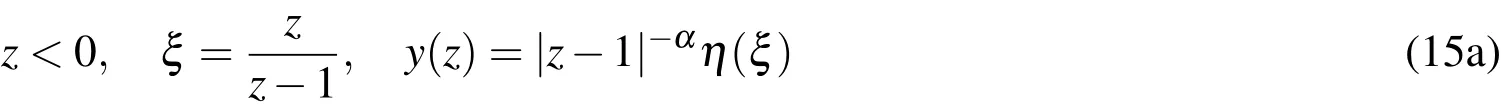
3 Results and discussion

In the simulation,both the outer and the inner boundaries are stress-free.The nondimensional expressions for the radial coordinate,the stress and the radial displacement are defined asand=u/(bα0ΔT),respectively.For simplicity,let=α1/α0and=E1/E0.The ratio of the inner and the outer radii is taken asa/b=0.5,throughout,which is reasonable for a thick-walled shell.

3.1 Displacements

As shown in Eqs.(14),the stresses and the radial displacement depend on the following factors:the ratio of the elastic moduli and the ratio of the thermal expansion coefficients of the two constituentsand,the Poisson ratioυ0,υ1and the inhomogeneity parameternwhich determines the contents of the compositions.Hence,the effects of these variables on stresses and displacement are discussed in the following,respectively.

In Figure 1,the radial displacementis plotted as a function of radius,with discussing dependencies onandin Figure 1(a),nin Figure 1(b),andυ1in Figure 1(c).

If the sphere is homogeneous,the displacement is given byu(r)=α0rΔT,which corresponds in Figure 1(a)to the case=1,which indeed appears as astraight line with a 1:l slope.When1,the local effective thermal expansion coefficient of the composite increases with radius,and the radial normal strainεrrconsequently increases withr,causing theu(r)curve to be concave upward.Conversely,when1,εrrdecreases withr,leading to a displacement curve that is concave downward.The conclusion is the same as that of Melanie P.Lutz and Robert W.Zimmerman(1996)for a FGM sphere.This effect is more obvious whenorυ1increase.It is also strengthened by the decreasingn,which means the reduced volume fraction of material B.The radial displacementuis sensitive to all of these variables mentioned above;therefore the effects of them are not negligible.

3.2 Thermal stresses

It is known that an unconstrained uniformly heated homogeneous hollow sphere would incurno thermal stresses.Hence the stresses in this simulation are purely a result of the inhomogeneous properties of the hollow sphere.The radial stressis shown in Figure 2,and the tangential(hoop)stressis shown in Figure 3.

When1,the local effective thermal expansion coefficient incre as es with radius,and so the out eredges of the sphere tend to expand more than the inneredges;this causes the hollow sphere to be under tensile radial stress.Conversely,if1,theouteredgesof the sphere tend toexp and less than the inneredges,the hollow sphere is consequently under compression.This dependency of the radial stress ongets even bigger whenorυ1rise.The radial stressσrris the largest in magnitude at some intermediate radius,which increases with the argumentnascends.

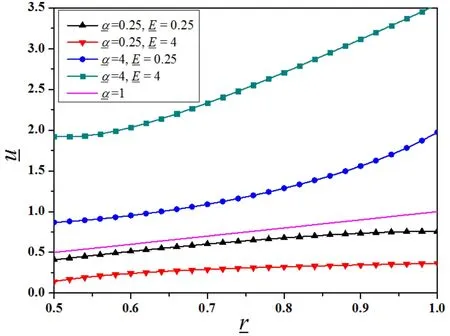
Figure 1(a):Evolution ofwith differentand(υ0=υ1=0.25,n=4)

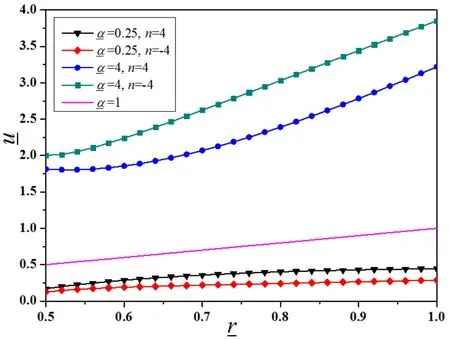
Figure 1(b):Evolution ofwith differentand n(υ0=υ1=0.25,=4).

Figure 1(c):Evolution ofwith differentand υ1(υ0=0.25,n=4,=4)

The hoop stress is the largest inmagnitude atone edge but is the opposite sign at the other edge,changing signs at some intermediate radius.These results are in qualitative agreement with the results found by Kolyano and Makhorkin(1976)for a two-shell sphere,Obata and Noda(1994)for a hollow FGM sphere and Robert W.Zimmerman and Melanie P.Lutz(1996)fora FGM sphere.

When1,the out eredges of the sphere tend to exp and more than the inneredges;this causes the inner part of the hollow sphere to be under tensile hoop stress,while the outer edges are consequently under compression in the hoop,and vice versa.The hoop stresses are monotonic functions of the radius.This effect ofis more obvious with the decreasing of.

The dependenciesonnandυ1arenotsmall.They influencenotonly on the magnitude but also the convexity of the hoop stress-rcurves.However,it is difficult to find a simple relationship between the hoop stresses and these arguments.It is suggested that increasingnand decreasingυ1lead to smaller hoop stresses in magnitude at the inner edge and larger ones at the outer edge.Furthermore,when1,amore strong tendency to be concave downward of the curves is shown with the decrease ofnbut increaseυ1.However,it is reverse when1.

Figure 2(a):Evolution ofr with differentand(υ0=υ1=0.25,n=4)

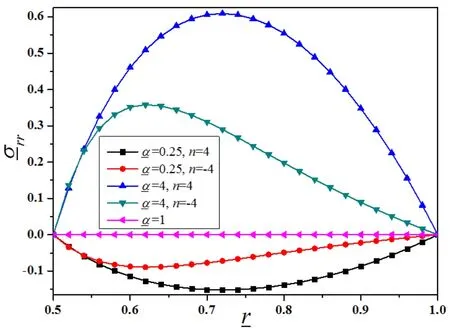
Figure 2(b):Evolution ofr with differentand n(υ0=υ1=0.25=4)

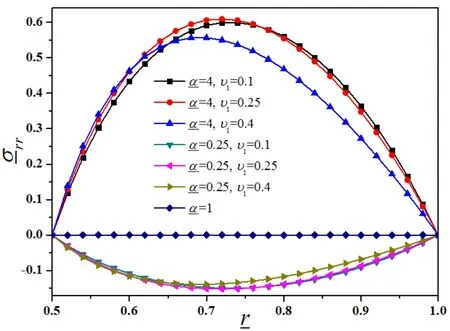
Figure 2(c):Evolution ofrr with differentand υ1(υ0=0.25,n=4,=4)

The deviatoric part of the stress tensor, which controls the onset of plastic deformation,attains it largest magnitude at the inner or outer edge of the hollow sphere,depending on the particular circumstances.

4 Effective coefficient of thermal expansion

It is known that if the temperature of an unconstrained homogeneous bodyVincreasesΔT,the total volume variation is 3αΔTV.Hence,the effective coefficient of thermal expansionαeffis

The volume variation of the hollow sphere related to the displacement field isgiven by

whereu(r)is the radial displacement.Combining Eq.(16)and(17)leads to

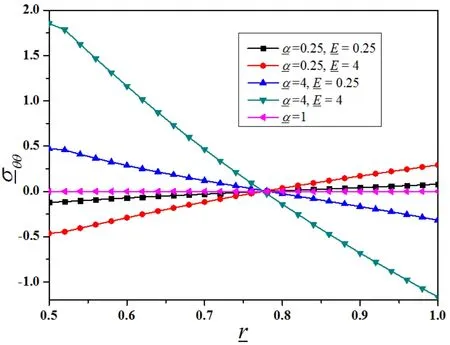
Figure 3(a):Evolution ofθθ with differentand(υ0=υ1=0.25,n=4)

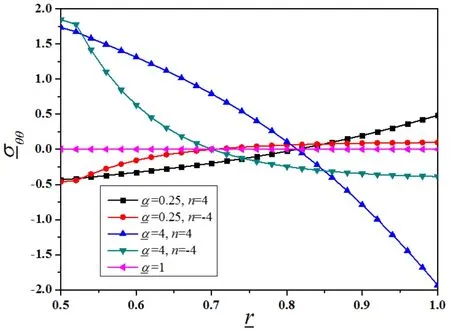
Figure 3(b):Evolution ofθθ with differentand n(υ0=υ1=0.25,=4)

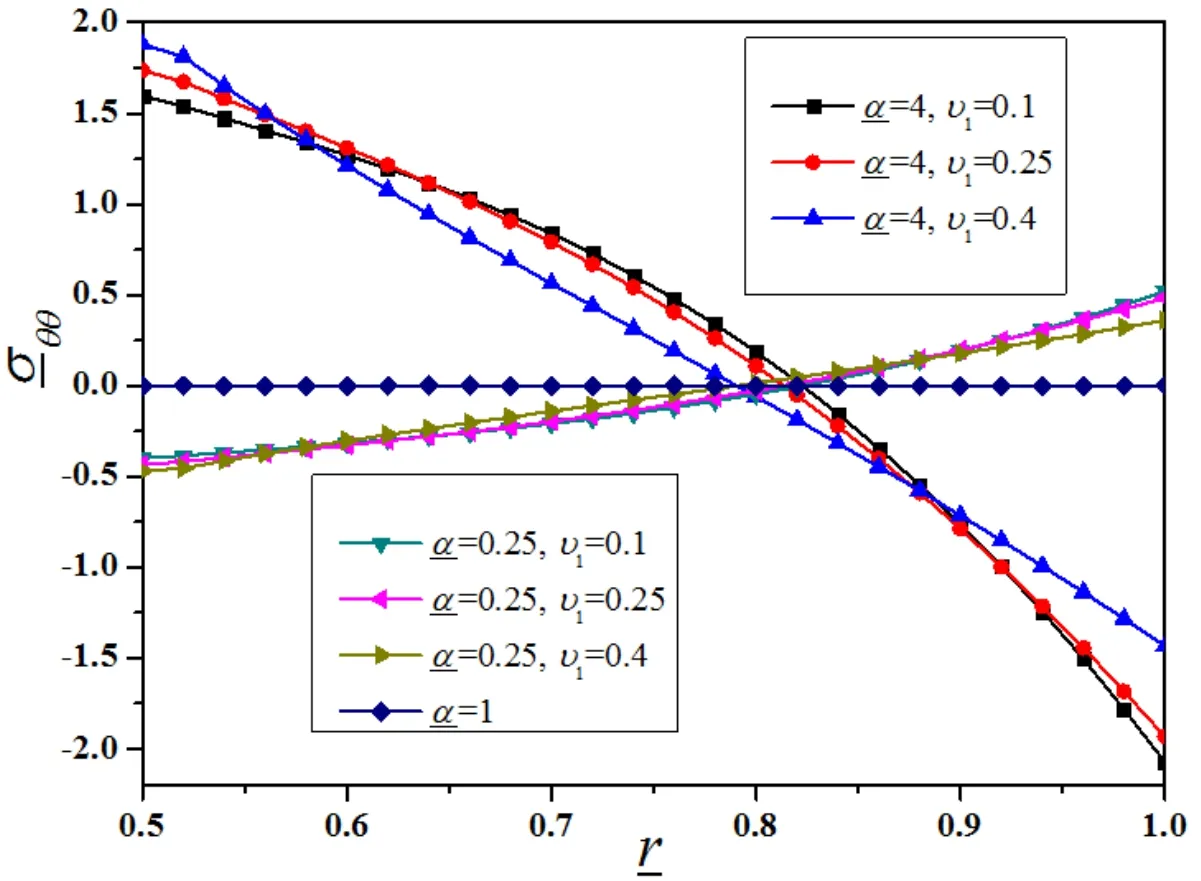
Figure 3(c):Evolution ofθθ with differentand υ1(υ0=0.25,n=4,=4)

Thenon-dimensional expressions for the the effective thermal expansion coefficient is defined asαeff=αeffα0and shown in Figure 4 asa function of.

Asshown in Eq.(18)and Figure 4,dependson,,υ0,υ1andn.The-curve is substantially a straight line through the point(1,1).The slope of the curve increases with the decrease ofn,which means an increasing volume fraction of material B.The increases of the relative valueυ1toυ0andalso lead to a larger slope.In addition,the magnitudes of the Poisson ratio has only a small effect on the effective thermal expansion coefficientifυ1=υ0.

5 Special cases of uniform moduli or thermal expansion coefficient

It is interesting to consider two special cases where either the elastic moduli or the thermal expansion coefficient varies,but not both.In the case where=1 throughout the hollow sphere,manipulating Eqs.(8)to(14),we get the solutionu=rα0ΔT.Combining Eq.(18),αeff=α0is found.Further,no thermal stress is induced,regardless of the variation in the elastic moduli.

Now consider the case of uniform elastic modulus but varied coefficient of thermal expansion.Then Eq.(8)can be written as:

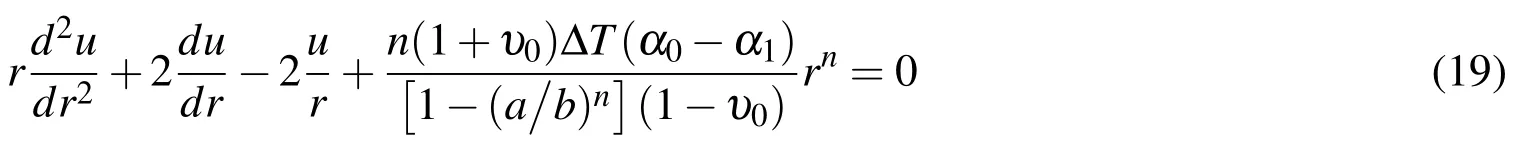
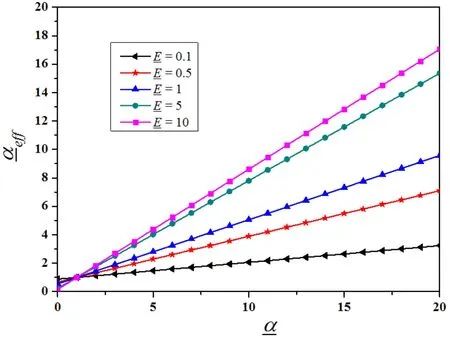
Figure 4(a):Evolution offf with different values of(υ0=υ1=0.25,n=4)

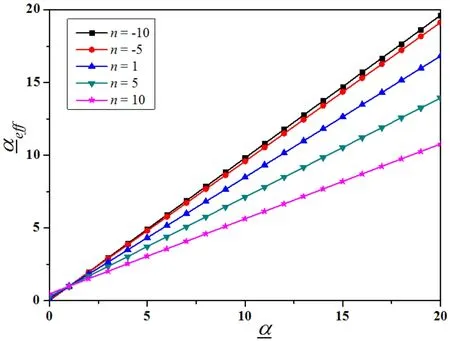
Figure 4(b):Evolution ofeff with different values of n(υ0=υ1=0.25,=4)

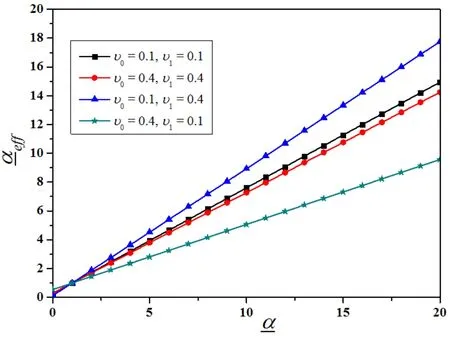
Figure 4(c):Evolution ofeff with different Poisson’s ratio( =4,n=4)

The general solution of the equation is

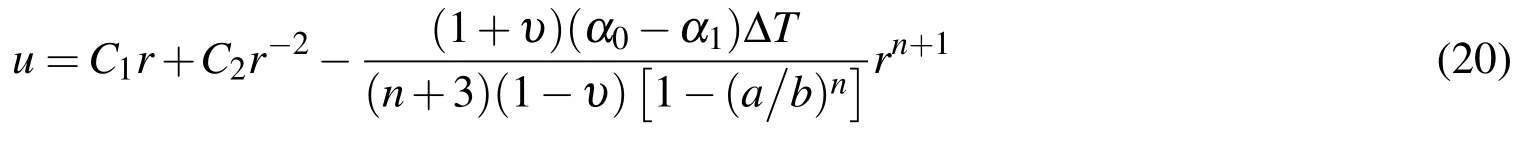
Substituting Eq.(20)into Eq.(18)yields

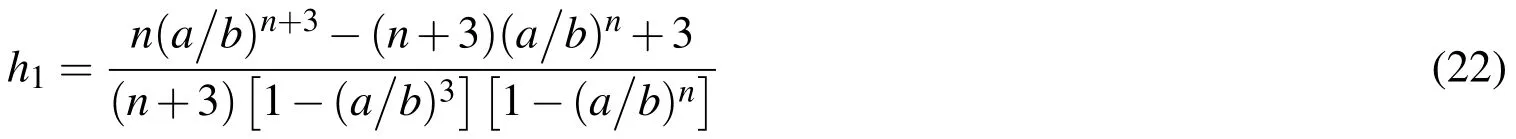
This result is precisely equal to the volumetric average of the local thermalexpansion coefficient,since

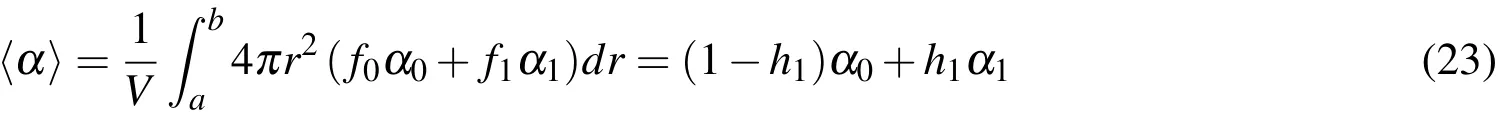
It concurs with that found by Robert W.Zimmerman and Melanie P.Lutz for a sphere(1996)and cylinder(1999)in which the thermal expansion coefficient varied linearly with radius.It is also consistent with Levin’s theorem,in the case in which the two components have identical elastic modules but different thermal expansion coefficients.

More generally,ifK0/=K1,Levin’s theorem(1967)predicts that the effective thermal expansion coefficient is given by

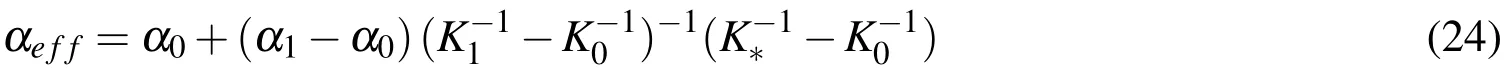
WhereK∗is the effective bulk module of the composite material.For convenience,take the volumetric mean as effective bulk module,thus we get

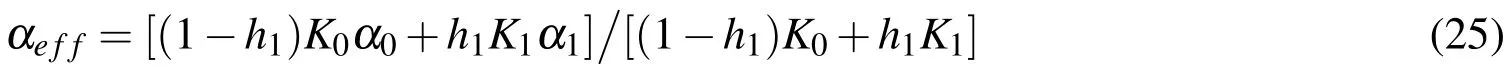
A comparison of the results obtained by present method and Levin’s theorem(Eq.(25))is shown in Figure 5.It shows that they are close to each other and Levin’s theorem leads to a larger slope.

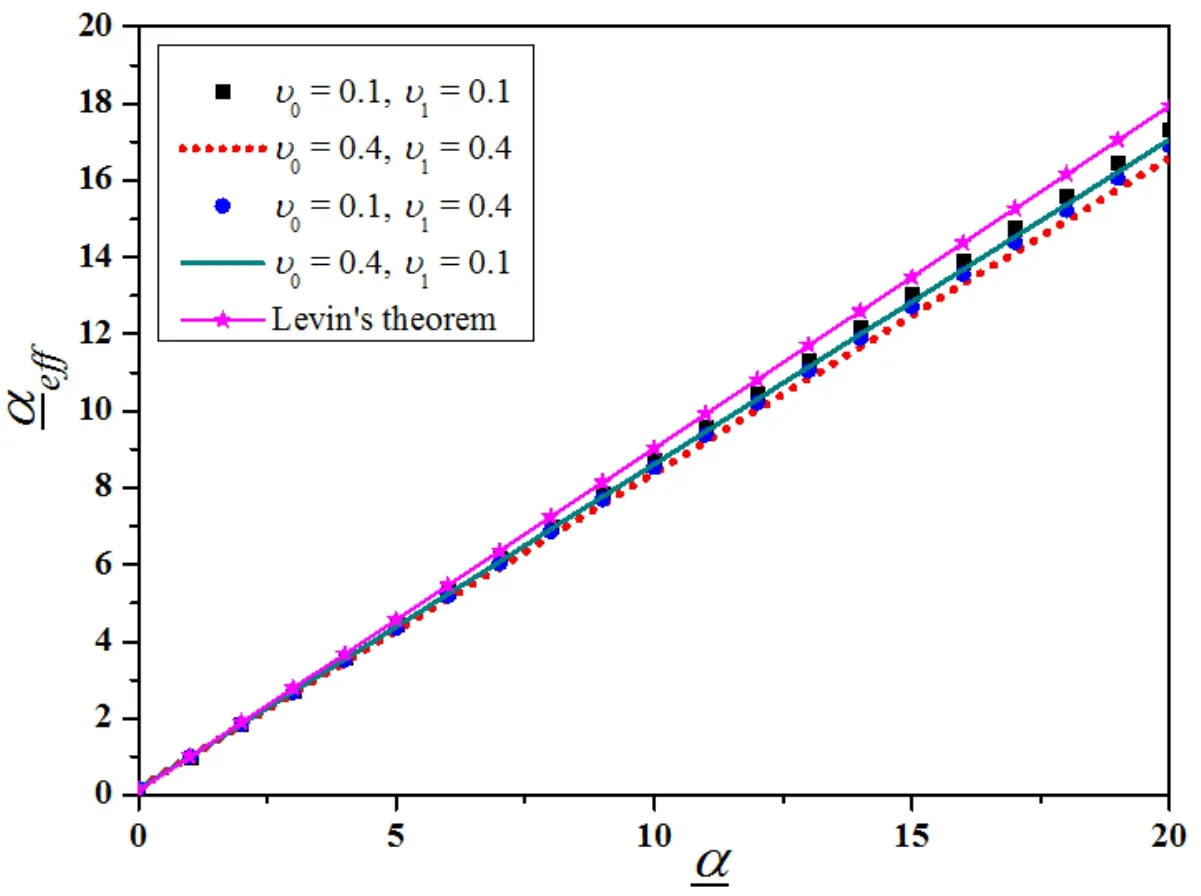
Figure 5:Comparison ofeff obtained with present methods and Levin’s theorem(K1/K0=10,n=4)

6 Summary and conclusions

Based on the Voigt constant strain approximation,an exact solution has been presented for the problem of the uniform heating of a functionally gradient hollow sphere made of two phase of different materials both of whose volume fractions vary with the radius.We found analytical expressions for the stress and displacement fields as well as for the effective thermal expansion coefficient.A ll of themdepend on the following factors:the ratio of the elastic moduli and the ratio of the thermal expansion coefficients of the two constituentsand,the Poisson ratioυ0,υ1and the inhomogeneity parameternwhich determines the contents of the compositions.

If1,u(r)curve is concave upward,the radial stress is positive(tensile),the hoop stress is positive at the inner edge and negativeat the outer edge of the hollow sphere,and vice versa.The effect is strengthened by the increase values ofE,αandυ1,but the decrease ofnandυ0.

The effective thermal expansion coefficient is nearly equal to the weighted averageby product of volume fractions and bulk modulus of the local thermal expansioncoefficient. In the special case where the elastic modules are uniform, the effectivethermal expansion coefficient is equal to the volume average of the local thermalexpansion coefficient. It is consistent with Levin’s theorem (1967) and the resultspresented by Robert W. Zimmerman and Melanie P. Lutz (1996, 1999).

Due to the linearity of the governing equations, this solution can be used to solvethe effective bulk modulus of a gradient hollow sphere. We have shown the thermalstress of a functionally gradient hollow sphere uniform heated, that with ununiformtemperature field is an interesting open question.

Alavi,F.;Karimi,D.;Bagri,A.(1993):An investigation on thermoelastic behaviourof functionally graded thick spherical vessel sunder combined thermal and mechanical loads.Journalof AchievementsinMaterials andManufacturingEngineering,vol.31,pp.422–428.

Dong,L.;Atluri,S.N.(2012):Development of 3 D Trefftz Voronoi Cells with Ellipsoidal Voids&/or Elastic/Rigid Inclusions for Micro mechanical Modeling of Heterogeneous Materials.CMC:Computers,Materials&Continua,vol.30,no.1,pp.39-82.

Dong,L.;Atluri,S.N.(2013a):Sgbem voronoi cells(svcs),with embedded arbitrary-shaped inclusions,voids,and/or cracks,for micro mechanical modeling of heterogeneous materials.CMC:Computers,Materials&Continua,vol.33,no.2,pp.111-154.

Dong,L.;Gamal,S.H.;Atluri,S.N.(2013b):Stochastic macro material prop-erties,through direct stochastic modeling of heterogeneous microstructures with randomness of constituent properties and topologies,by using trefftz computational grains(TCG).CMC:Computers,Materials&Continua,vol.37,no.1,pp.1-21.

Eslami,M.R.;Babaei,M.H.;Poultangari,R.(2005):Thermal and mechanical stresses in functionally graded thick sphere.International Journal of Pressure Vessels and Piping,vol.82,pp.522–527.

Fukui,Y.;Yamanaka,N.;Wakashima,K.(1993):The stresses and strains in a thick-walled tube for functionally graded material under uniform thermal loading.JSME international journal.Series A,mechanics and material engineering,vol.36,no.2,pp.156–162.

Jabbari,M.;Sohrabpour,S.;Eslami,M.R.(2002):Mechanical and thermal stresses in functionally graded hollow cylinder due to radially symmetric loads.Int.J.Pressure Vessel Piping,vol.79,pp.493–497.

Jabbari,M.;Sohrabpour,S.;Eslami,M.R.(2003):General solution formechanicaland thermalstresses in a functionally graded hollow cylinder due to nonaxisymmetric steady-state loads.ASMEJAppl.Mech.,vol.70,pp.111–118.

Jabbari,M.;Vaghari,A.R.;Bahtui,A.;Eslami,M.R.(2008):Exact solution for asymmetric transient thermal and mechanical stresses in FGM hollow cylinders with heat source.Structural Engineering and Mechanics,vol.29,pp.551–565.

Jeon,S.P.;Tanigawa,Y.;Sone,D.(1997):Analytical treatment of axisym metrical thermoelastic field with Kassir’s on homogeneous material properties and its adaptation to boundary value problem of slab under steady temperature field.J.Therm.Stress,vol.20,pp.325–343.

K im,K.S.;Noda,N.(2002a):Green’s function approach to unsteady thermal stresses in an infinite hollow cylinder of functionally graded material.Acta.Mech.,vol.156,pp.142–161.

Kim,K.S.;Noda,N.(2002b):A Green’s function approach to the deflection of a FGM plate under transient thermal loading.Arch.Appl.Mech.,vol.72,pp.127–137.

Kolyano,M.;Makhorkin,I.N.(1976):Thermal Stresses in a Spherical Thick-Walled Shell with a Filler.Strengrh Muter.,vol.8,pp.1337–1340.

Kwon,P.;Dharan,C.K.H.;Ferrari,M.(1994):Macroscopic Analysis of Axisymmetric Functionally’-Gradient Materials under Thermal Loading.Journal of energy resources technology,vol.116,pp.115–120.

Levin,V.M.(1967):Thermal Expansion Coefficients of Heterogeneous Materials.Mech.Solids,vol.2,pp.458–461.

Lutz,M.P.;Zimmerman,R.W.(1996):Thermal stresses and effective thermal expansion coefficient of a functionally graded sphere.J Therm Stress,vol.19,pp.39–54.

Nadeau,J.C.;Ferrari,M.(1999):Micro structural optimization of functionally graded transversely isotropic layer.Mechanics of Materials,vol.31,pp.637–651.

Obata,Y.;Noda,N.(1994):Steady Thermal Stresses in a Hollow Circular Cylinder and a Hollow Sphere of a Functionally Gradient Material.J.Thermal Stresses,vol.17,pp.471–487.

Poultangaria,R.;Jabbari,M.;Eslami,M.R.(2008):Functionally graded hollow spheres under non-axisymmetric thermo-mechanical loads.International Journal of Pressure Vessels and Piping,vol.85,pp.295–305.

Sadeghian,M.;Toussi,H.E.(2011):Axisymmetric yielding of functionally graded spherical vessel under thermo-mechanical loading.Computational Materials Science,vol.50,pp.975–981.

Sladek,J.;Sladek,V.;Solek,P.;Tan,C.L.;Zhang,C.(2009):Two-and three dimensional transient thermoelastic analysis by the MLPG method.CMES:Computer Modeling in Engineering &Sciences,vol.47,no.1,pp.61.

Sladek,J.;Sladek,V.;Solek,P.;Wen,P.H.(2008a):Thermal bending of Reissner-Mindlin plates by the MLPG.CMES:Computer Modeling in Engineering&Sciences,vol.28,no.1,pp.57–76.

Sladek,J.;Sladek,V.;Solek,P.;Wen,P.H.;Atluri,S.N.(2008b):Thermal analysis of Reissner-Mindlin shallow shells with FGM properties by the MLPG.CMES:Computer Modeling in Engineering&Sciences,vol.30,no.2,pp.77–97.

Sladek,J.;Sladek,V.;Tan,C.L.;Atluri,S.N.(2008c):Analysis of transientheat conduction in 3D anisotropic functionally graded solids,by the MLPG method.CMES:Computer Modeling in Engineering&Sciences,vol.32,no.3,pp.161–174.

Sugano,Y.(1990):An Analytical Solution for a Plane Thermal Stress Problem in Nonhomogeneous Multiply Connected Regions.JSME Int.J.Ser.I,vol.33,pp.136–144.

Wang,B.L.;Mai,Y.W.(2005):Transient one-dimensional heat conduction problems solved by finite element.International Journal of Mechanical Sciences,vol.47,pp.303–317.

Zimmerman,R.W.;Lutz,M.P.(1999):Thermal stress and effective thermal expansion in a uniform ly heated functionally graded cylinder.JTherm Stress,vol.22,pp.177–188.