Buckley-Leverett Analysis for Transient Two-phase Flow in Fractal Porous Medium

Yonggang Duan, Ting Lu, Mingqiang Wei, Boming Yu and Zhelun Zhang

1 Introduction

Petroleum reservoir engineering problems especially in porous media are known tobe inherently nonlinear. Consequently, solutions to the complete multiphase flowequations have been principally attempted with numerical methods. However, simplifiedforms of the problem were solved some 60 years ago, when the Buckley-Leverett formulation was introduced. The Buckley-Leverett displacement theorywas applied to petroleum reservoirs engineering consisting of a finite number oflayers [Snyder and Ramey (1967)]. Internal consistency requires that the parametersshould be corrected for the removal of interfacial tension because capillarypressure was ignored in the Buckley-Leverett analysis [Spanos, De La Cruz andHube (1986)]. Mohsen (1985) found that a mass-conserving front would be locatedfarther down the flow direction for a nonzero initial condition and discussed theimplications of this finding for error analysis in comparing numerical solutions tothe analytical one. Larsen, Kviljo and Litlehamar (1990) examined the relationshipbetween backflow of water from the invaded zone and changed in skin owing toreduced water saturation and the associated change in mobility for homogeneousreservoirs with Buckley-Leverett methods. Langtangen, Tveito andWinther (1992)studied the simultaneous one-dimensional flow of water and oil in a heterogeneousmedium modeled by the Buckley-Leverett equation. A variety of heterogeneityprofiles were studied with Buckley-Leverett methods Capillary heterogeneity significantlyaffects the saturation distributions, which closely follow the heterogeneityvariation [Chang and Yortsos (1992)] The geothermal saturation wave speedunder all conditions is formally identical with the Buckley-Leverett wave speedwhen the latter is written as the saturation derivative of a volumetric flow [Young(1993)]. A Buckley-Leverett-type analytical solution for one dimensional immiscibledisplacement was presented in a linear composite porous medium [Wu, Pruessand Chen (1993)]. Frid (1995) solved the initial boundary-value problem for theregularized Buckley-Leverett system, which described the flow of two immiscibleincompressible fluids through a porous medium The measurement of three-phaserelative permeability using the extension of the Buckley-Leverett theory has bothsound theoretical and experimental bases [Siddiqui, Hicks and Grader (1996)]. Anexperimental investigation was made to test the validity of the three-phase extensionof the Buckley-Leverett (B-L) theory using three immiscible liquids [Siddiqui,Hicks and Grader (1996)]. Method of characteristics (MOC) solutions to the threephaseBuckleyLeverett problem was presented with and without gravity [Guzmanand Fayers (1997)]. Terez and Firoozabadi (1999) examined water injection inwater-wet fractured porous media and its modeling using the Buckley–Leveretttheory. A stochastic analysis of immiscible two-phase flow with Buckley–Leverettdisplacement was presented in heterogeneous reservoirs [Dongxiao and Tchelepi(1999)]. Kaasschieter (1999) derived an entropy inequality from a regularizationprocedure, where the physical capillary pressure term is added to the Buckley-Leverett equation. An extension of the Buckley–Leverett (BL) equation describingtwo-phase flow in porous media was discussed by Van Duijn, Peletier and Pop(2007). Mustafiz, Mousavizadegan and Islam (2008) used a semi-analytical techniqueand the Adomian decomposition method (ADM) to unravel the true nature ofthe one-dimensional, two-phase flow. Sumnu-Dindoruk and Dindoruk (2008) havesolved the resulting nonisothermal two-phase convective flow equation in porousmedia analytically, including a tracer component. A new approach was proposed tothe mathematical modeling of the Buckley–Leverett system, which describes twophaseflows in porous media [Chemetov and Neves (2013)]. Wang and Kao (2013)extended the second and third order classical central schemes for the hyperbolicconservation laws to solve the modified Buckley Leverett (MBL) equation which isof pseudo-parabolic type. Wang and Kao (2014) numerically verified that the convergencerate is consistent with the theoretical derivation by BuckleyLeverett (BL)equation.

It’s well known that the microstructures of real porous medium are usually disorderedand extremely complicated. Fortunately, it has been shown that the microstructuresof porous medium have the self-similarity and fractal characteristics[Katz and Thompson (1985); Xiao, Jiang, and Chen (2010)]. The pore spacesof several sandstones are fractal geometries by using the scanning electron microscopyand optical data [Katz and Thompson (1985)]. The pore-size distributionfractal model of unsaturated soils was derived and Hydraulic conductivity andsoil-water diffusivity of unsaturated soils could be expressed by two fractal parameters[Xu and Dong (2004)]. Completely multi-scale configurations can guide theflowing in porous medium based on the application of tree-shaped fractal structures[Lorente and Bejan (2006)]. Deinert, Dathe, and Parlange (2008) presentedthat the relationship between capillary pressure and saturation in a fractal porousmedium and exhibited a power-law. A fractal model for the relative permeabilityof porous medium was presented by assuming that porous medium consists of abundle of tortuous capillaries, but the effects of capillary pressure was not considered[Yu and Liu (2004)]. Based on [Yu and Liu (2004)], the relative permeabilityof unsaturated porous medium embedded with a fractal-like tree branched networkswas studied by considering the capillary pressure [Wang and Yu (2011)]. Xu, Qiu,Yu, and Jiang (2013) investigated the relative permeability in unsaturated porousmedium by assuming that all capillaries with the radius less than a critical radiusare saturated, and the others with the radius larger than the critical radius are unsaturated.Recently, a generalized fractal model was developed for spontaneousimbibition in porous medium with shapes of pores included [Cai, Perfect, Cheng,and Hu (2014)]. Based on the fractal characteristics of pore size distribution and onthe approximation that porous medium consists of a bundle of tortuous capillaries arelative permeability model for transient two-phase flow in fractal porous mediumwas derived [Tan, Li, and Liu (2014)]. For fractal systems, the pore or solid maybe fractal. For pore fractal, mass fractal and pore-solid fractal, recent review workis helpful to understand [Cai, Luo, and Ye (2015)].

But it is difficult to apply Buckley-Leverett equation to solve petroleum reservoirengineering problems in porous medium saturated with multiphase fluid becausethe microstructures of real porous medium are usually disordered and extremelycomplicated. However, quite a few scholars have done excellent job to studypetroleum reservoir engineering problems using Buckley-Leverett equation and research the microstructure of porous media with fractal theory in recent few decades.Thus, we pay close attention to Buckley-Leverett model based on fractal theory inporous media.

In this thesis, we continue a line of research on Buckley-Leverett analysis fortransient two-phase flow in fractal porous media based on fractional flow analysiswhich is our previous work entitled “Analysis of the fractional flow for transienttwo-phase flow in fractal porous media” (under review). The purpose of the presentpaper is to derive an analytical expression for Buckley-Leverett solution based onthe fractal geometry theory for porous medium, and it is expected the proposedfractal expression for the front position to compute water saturation profile.

This paper is organized as follows. In Sect. 2, the relevant theoretical bases whichmainly include velocity and flow rate of transient two-phase flow in a single capillaryare introduced. In Sect. 3, on the approximation that porous media consistsof a bundle of tortuous capillaries, an analytical expression for Buckley-Leverettsolution is derived based on the fractal characteristics of pore size distribution Theresults and discussion are shown in Sect. 4. Eventually, we summarize the conclusionsin Sect. 5

2 Theoretical Bases

We approximate that porous media is comprised of a bundle of tortuous capillaries with different diameters.According to this approximation,a single fractal capillary with transient two-phase flow is proposed here,as shown in Fig.1 The fractal capillary is only saturated with oil(red)initially,but later water(blue)intrudes into the capillary and displaces oil with a constant pressure difference between pointsaandb.Therefore,the fractal capillary is separated by a two-phase flow interfaceat pointc.The constant pressure difference bet ween pointsaandbisΔP.The fractal capillary diameter,the straight distance of the capillary,and the straight distance between pointsaandcareλ,L,andXrespectively.

Figure 1:A single fractal capillary with transient two-phase flow.

Tan,Li,and Liu(2014)presented a theoretical analytical expression for the transient twophase flow velocity in a single capillary

whereµwandµoare the viscosity of water and oil,respectively.λis the capillary diameter,XTis the actual length of the capillary between pointsaandc,andLTis the actual length of the capillary.ΔPis the constant pressure difference between pointsaandb,andPCis capillary pressure.

The fractal scaling law for tortuous capillaries in porous medium is given by Yu and Cheng(2002)

and

whereDTis the tortuosity fractal dimension.

The capillary pressure function can be expressed as:

whereσis surface tension,θis contactangle.

Substituting Eqs.(1)–(2)into Eq.(4)the expression of two-phase flow velocityvcan beobtained as:

From Eq.(5),we can get the expression of the two-phase flow rateqt,in a single tortuous capillary:

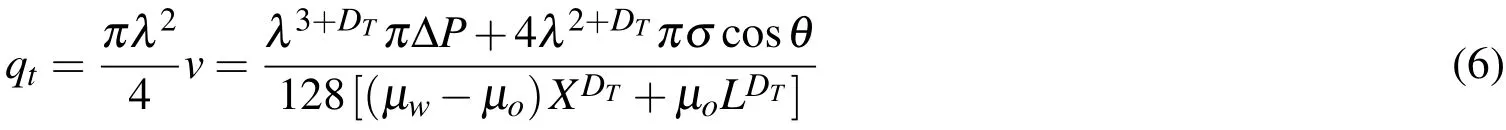
In Eq.(6),whenσ=0,X=L,the two-phase flow rate can be regarded as singlephase flow rate,qs,which is expressed as

Equation (7) is the same as the expression of the single-phase flow rate in a single fractal capillary by Yu and Cheng (2002).

It is known that

Combining Eq. (5) and Eq (8),we get the expression of the two-phase flow velocity in a single capillary

From Eq. (3),we get

Substituting Eq. (10) into Eq. (9),we can yield

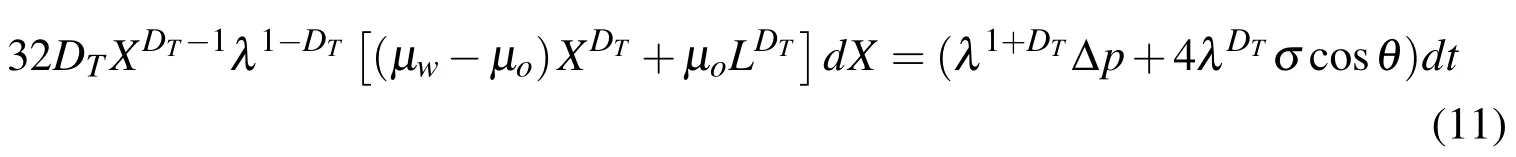
Taking an integration of Eq. (11)with initial conditiont=0 andX=0,and after rearranging,we get the relationship between the two-phase interface position,X,and relevantdisplace timet

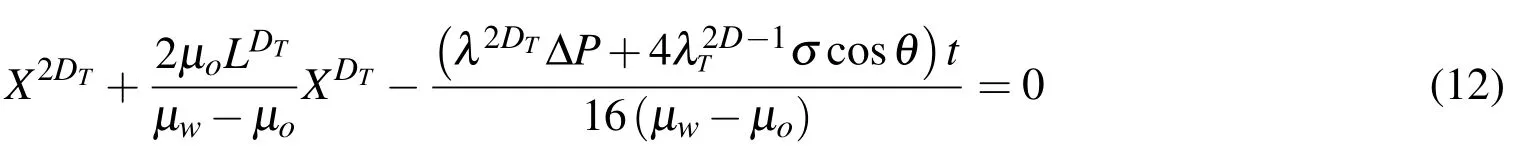
From Eq. (12) we can see that whenX=0 andt=0 the capillary is only saturated with oil.0＜X＜Lrepresents the flow regime in capillary is transient two-phase flow.WhenX=L,oil is completely displaced by water.SubstitutingX=Linto Eq. (12),the expression for completely displacing time,td,can bew ritten as

Eq. (13) reveals that the completely displacing time is greatly affected by fractal parameters and fluid properties.Since the fractal porous medium is assumed to be comprised of a bundle of tortuous capillaries with different diameters,we only discuss the influence of the capillary diameter on the completely displacing time.Assuming other parameters (viscosities of water and oil,tortuosity fractal dimension,the difference pressure,contact angle and interfacial tension) are constant,abigger capillary diameter corresponds to a smaller value of displacement time.That is to say,it will take less time for water to displace oil completely in a capillary with bigger diameter.

Here we define the critical capillary diameter,λcr,to be the capillary diameter [Xu,Qiu,Yu,and Jiang (2013)],at which oil is just right displaced by water completely at a given time.Substitutingtd=tinto Eq. (13),we obtain the following equation for the critical diameter as:

From Eq. (14),we can see that the critical capillary diameter is affected by fluid properties (such as contact angle,viscosities,pressure difference and interfacial tension) and the fractal dimensionDT.Here,we particularly emphasize on analyzing how time impacts the critical capillary diameter.It is easily to see that the critical capillary diameter becomes smaller with the increase of displacement time and more and more capillaries will change its flow regime from transient two-phase flow to single-phase flow.Thus,ifλ ≥λcr,oil is displaced by water completely and water flows out pointbof the capillary.Otherwise,oil is not displaced by water completely and oil flows out pointbof the capillary.

3 A Model for Buckley-Leverett solution

It has been shown that the cumulative size-distribution of capillary sizes which are greater than or equal to the capillary diameter,λ,follows the fractal scaling law [Yu and Cheng (2002)]:

whereλmaxis the maximum diameter of capillary,andDfis pore fractal dimension.Generally,0＜Df＜2 denotes two dimensional space,and 0＜Df＜3 refers to three dimensional space.

Since there are numerous pores in a sample porous medium,Eq. (15) can be approximately considered as a continuous and differentiable function.Then,taking derivative with respect to diameter in Eq.(15)yields the number of pores whose diameters are within the infinitesimal range ofλandλ+dλ.

Based on the approximation that porous medium consist of a bundle of tortuous fractal capillaries with variable diametersand on the fractal characteristics of poresize distribution in porous medium, we can derive Buckley-Leverett solution modelof transient two-phase flow in a fractal porous medium as shown in Fig. 2.

Figure 2:Transient two-phase flow in a porous medium with tortuous capillaries at a given time.

As is shown in Fig.2,water flows out of cross-sectionBin fractal capillaries whose diameters are larger than the critical capillary diameter and it is single-phase flow in these capillaries.On the contrary,if capillary diameter is smaller than the critical capillary diameter,oil flows out of cross-sectionB(or water cannot flow out cross sectionB)and it is transient two-phase flow.

We can get the total flow rate,Qby summing up the flow rates through all the capillaries at the cross-sectionB.

The total flow rate of water,Qw,atacross-sectionBcan be obtained by integrating Eq.(14)from critical capillary diameter to maximum diameter.

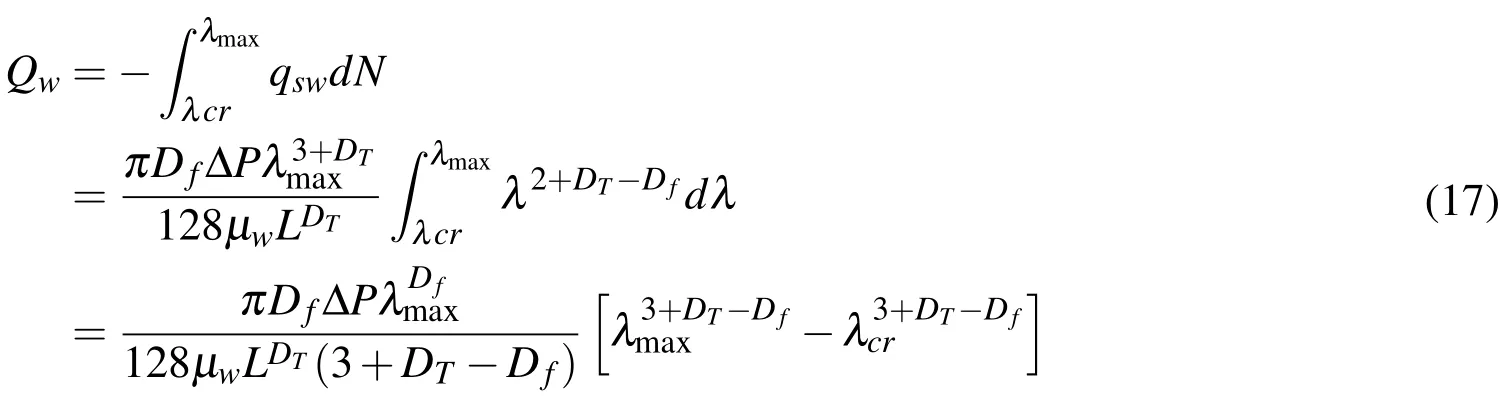
While oil flows out of across-sectionBin fractal capillaries whose diameters are smaller than the critical capillary diameter. Because oil is not completely displaced by water,flow pattern is still two-phase flow The total flow rateofoil,Qoatsection planeBcan beobtained by integrating Eq.(13)from minimum diameter to criticalcapillary diameter.

whereλcris the critical capillary diameter.Based on the fractal theory,the total pore volume in the fractal porous medium can beex pressed as

As is seen from Fig.2,the pore volume of the fractal porous medium saturated with water is composed of two portions:the whole capillary volume whose flow regime is single-phase flow and the back part of capillary volume whose flow regime is transient two-phase flow.

The pore volume of the fractal porous medium saturated with oil is only the front part of capillary volume whose flow regime is transient two-phase flow.

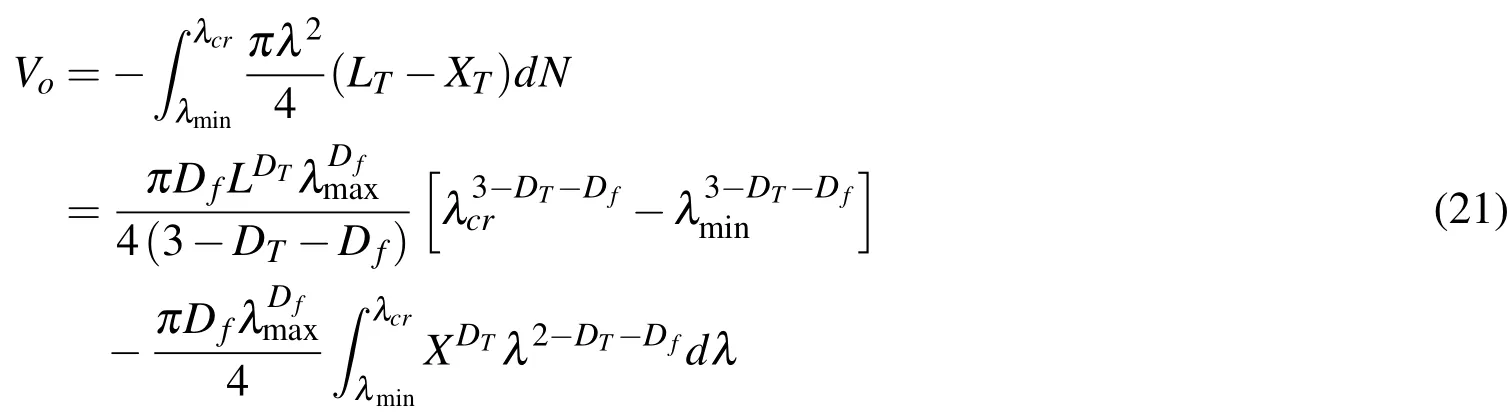
Combining Eqs.(19)-(21),saturation of water,Sw,and saturation of oilSocan be respectively expressed as:

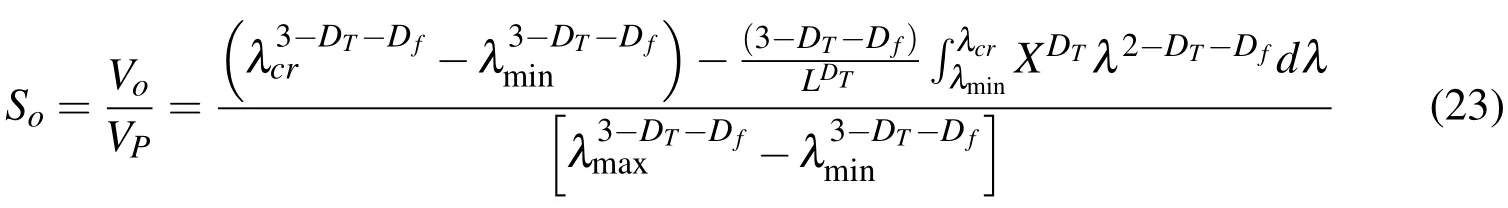
In Eqs.(20)and(23),whenX=Landλcr=λmax,oil is completely displaced by water,soSw=1andSo=0WhileX=0andλcr=λminin Eqs.(20)and(23),the fractal porous medium is only saturated with oil,thusSw=0 andSo=1.

Fractional flow of water,fw,can be defined as the proportion of flow rate of water in the total flow rate.So fractional flow of water can be expressed as

Substituting Eqs(17)and(18)into Eq.(24),fractional flow of water can be expressed as:

From Eq.(25),we can see that fractional flow of water relates to not only fractalstructural parameters (such as tortuosity fractal dimension, pore fractal dimension,maximum and minimum diameters of capillaries) but also fluid properties (such ascontact angle, viscosity and interfacial tension). That is to say, both fractal porousmedium and relevant fluid properties may have important impacts on fractionalflow of water. Fractional flow of water is the proportion of flow rate of water inthe total flow rate. So if water dominates the flow in a fractal porous medium, thefractional flow value of water is larger. More details will be shown in Sect. 4

In this paper,we use weighted method to differentiate fractional flow of water.Thederivative of fractional flow of water can be expressed as:

wherefw jis the fractional flow of water at thejthtime step.fw j-1is the fractional flow of water at the(j-1)thtime step.fw j+1is the fractional flow of water at the(j+1)thtime step.Sw jis the saturation of water at thejthtime step.Sw j-1is the saturation of water at the(j-1)thtime step.Sw j+1is the saturation of water at the(j+1)thtime step.

Eq.(26)represents first order-derivative of fractional flow of water with respect to independent variable saturation of water.f′w(Sw)is the rate of change in fractional flow of water with saturation of fluid and it can help us to determine the frontal advance equation.

From Eq.(24),we can get

So

wherevtis the total velocity of water and oil

Differentiating Eq.(28)with respect tox,we yield

Combining Eq.(29)and Eq.(30),we can get the following expression after arranging:

If we ignore the compressibility of rock and fluid,the total velocity is constant andfwis the function ofSwwhen the flow regime is steady.i.eSw=C anddSw=0

After arranging,we can get the following expression:

Combining Eq.(32)and Eq.(33)

Eq.(34)is single phase flow equal saturation plane moving equation which is alsocalled Buckley-Leverett equation.

It is known that

whereq(t)is the feed water rate of injection.

Substituting Eq.(35)into Eq.(34),weget

Taking an integration of Eq.(36),we yield

wherexis the beginning location of transient two phase flow,andxisany location of transient two phase flow.

From Eq.(37),we can see that

Based on the fractal theory,the total area of pore can be expressed as the following:

and porosity can be expressed as follows[Yu and Li(2001)]:

Substituting Eqs.(39)and(40)into Eq.(38),we get the expression of water saturation profile:

4 Results and Discussion

Figure 3 shows a typical plot of fractional flow and its derivative curve based on the predictive model of Eq.(25)and Eq.(26).Figure 3 shows an increase in fractional flow of waterfw(Sw)when the saturation of water,Sw,goesup

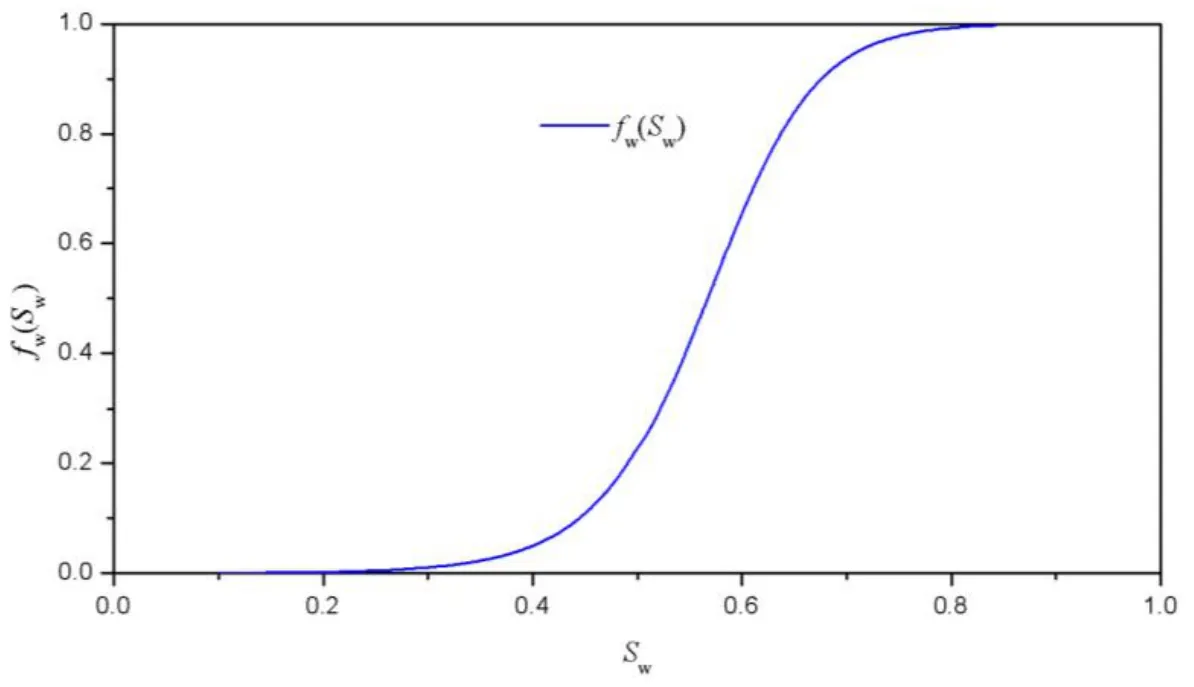
Figure 3:Fractional flow curve.(µw=1×10-3Pa.s, µo=1.2×10-3Pa.s, σ=0.06N/m, θ=0.5, L=1×10-2m,λmax=1.5×10-4m,λmin=0.2×10-7m,ΔP=5×105Pa,DT=1.14,Df=1.7)

The determination of the water saturation at the front is shown graphically in Fig.4.

Using the expression for the front position,and plotting water saturation vs.distance,we get the Fig.5.

Clearly,the plot of saturation is showing an impossible physical situation,since we have two saturationsateachx-position.However,this is a result of the discontinuity in the saturation function,and the Buckley-Leverett solution to this problem is to modify the plot by defining a saturation discontinuity atxfand balancing of the areas ahead of the front and below the curve,as shown in Fig.6.

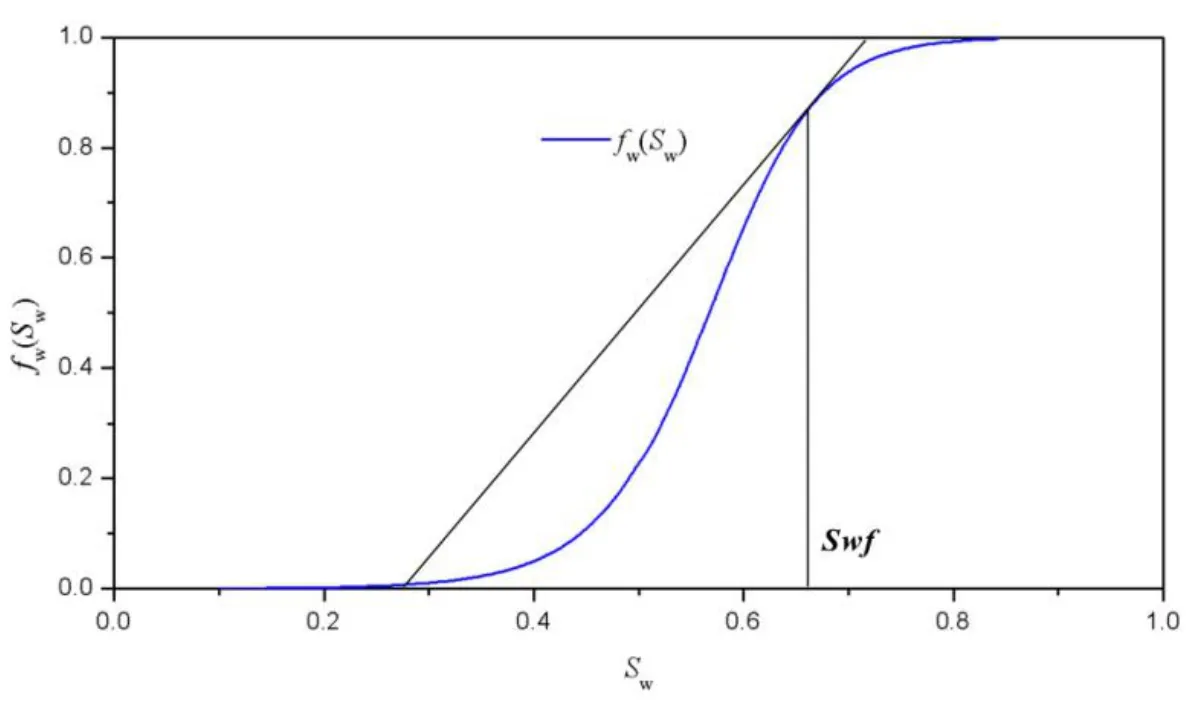
Figure 4:Determination of water saturation at the front.

Figure 5:Computed water saturation profile.

The final saturation profile thus becomes Fig.7.

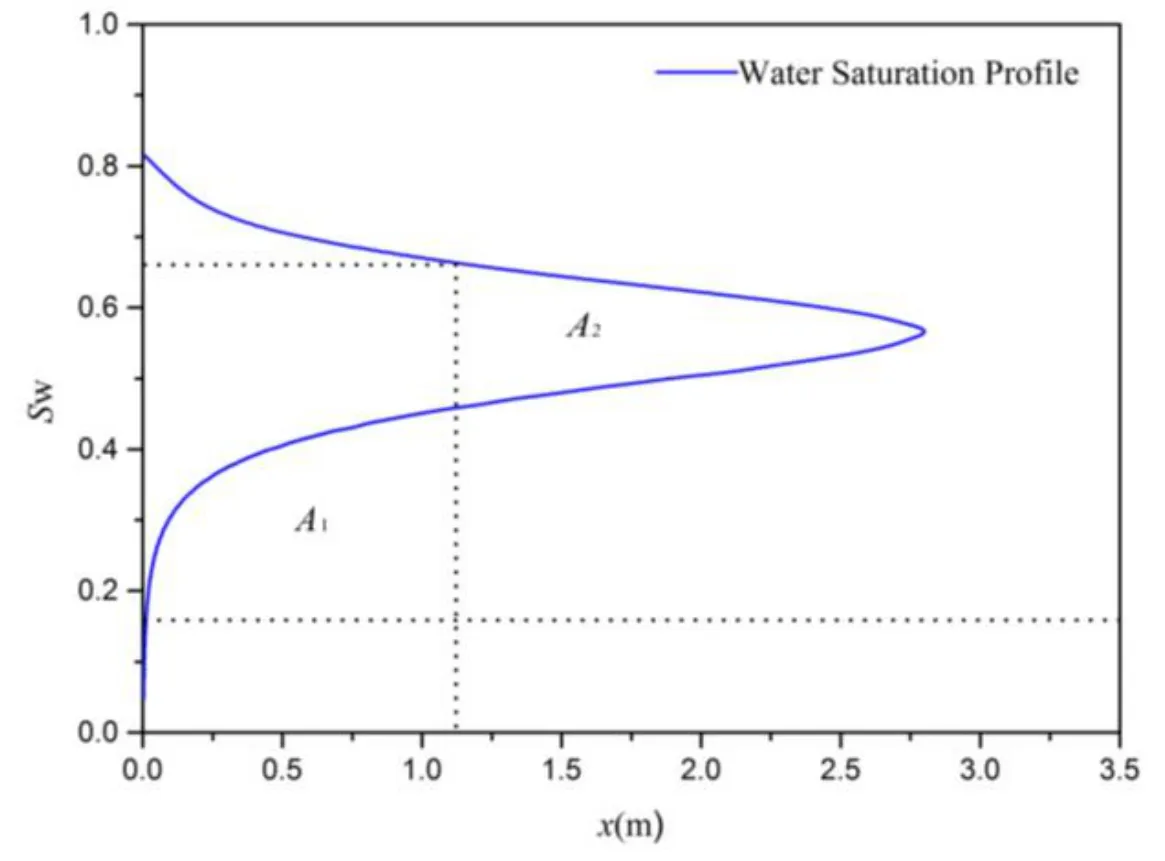
Figure 6:Balancing of areas.

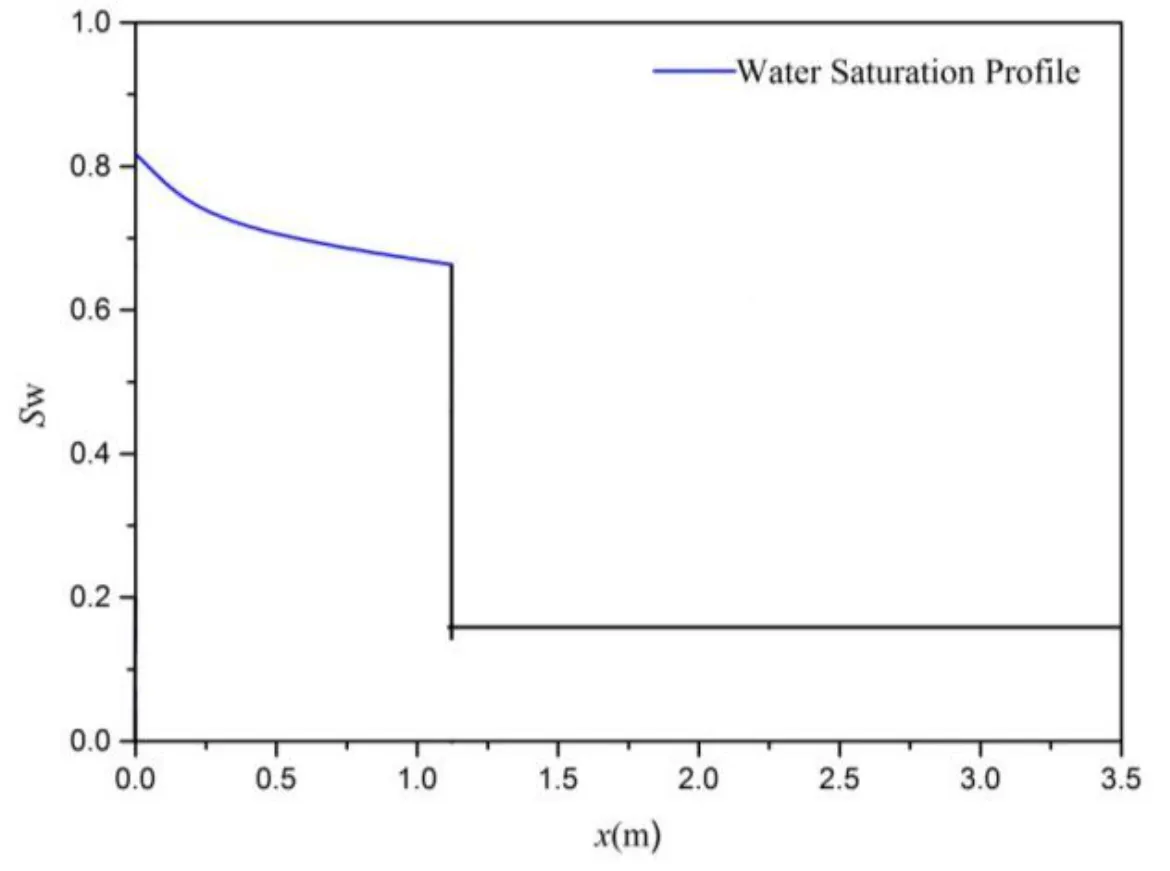
Figure 7:Final water saturation profile.

From Eq.(41),we can see that water saturation profile is affected by fractal structuralparameters (such as pore fractal dimension, tortuosity fractal dimension, maximumand minimum diameters of capillaries) and fluid properties (such as viscosity,contact angle and interfacial tension) in fractal porous medium. we emphaticallyanalysis the affection of pore fractal dimension, tortuosity fractal dimension, maximumand minimum diameters of capillaries on water saturation profile.

Figures8-11 show that water saturation vs.distance at different pore fractal dimensions,Df,and tortuosity fractal dimension,DT,respectively.

Figure 8:Computed water saturation profile affected by Df.

Dfrepresents the cross-sectional distribution of pores in porous medium. The heterogeneityof porous medium increases and the distributions of fluids 1 and 2 infractal porous medium become more complex with the increase of Df. Thus thevalue of two-phase position is smaller at the same water saturation with the increase ofDfas is shown in Fig.9.This implies it becomes harder for water to displace oil completely with the increase ofDf.

DTrepresents the tortuosity of capillaries in porousmedium.The flow path length of fluid in a porous medium increases with the increase ofDT,which indicatesa higher flow resistance in a fractal porous medium. Thus the heterogeneity ofa porous medium enhances and the distributions of oil and water in fractal porousmedium become more complicated. Thus the value of two-phase position is smallerat the same water saturation with the increase ofDTas is shown in Fig.11.This implies it becomes harder for water to displace oil completely with the increase ofDT.

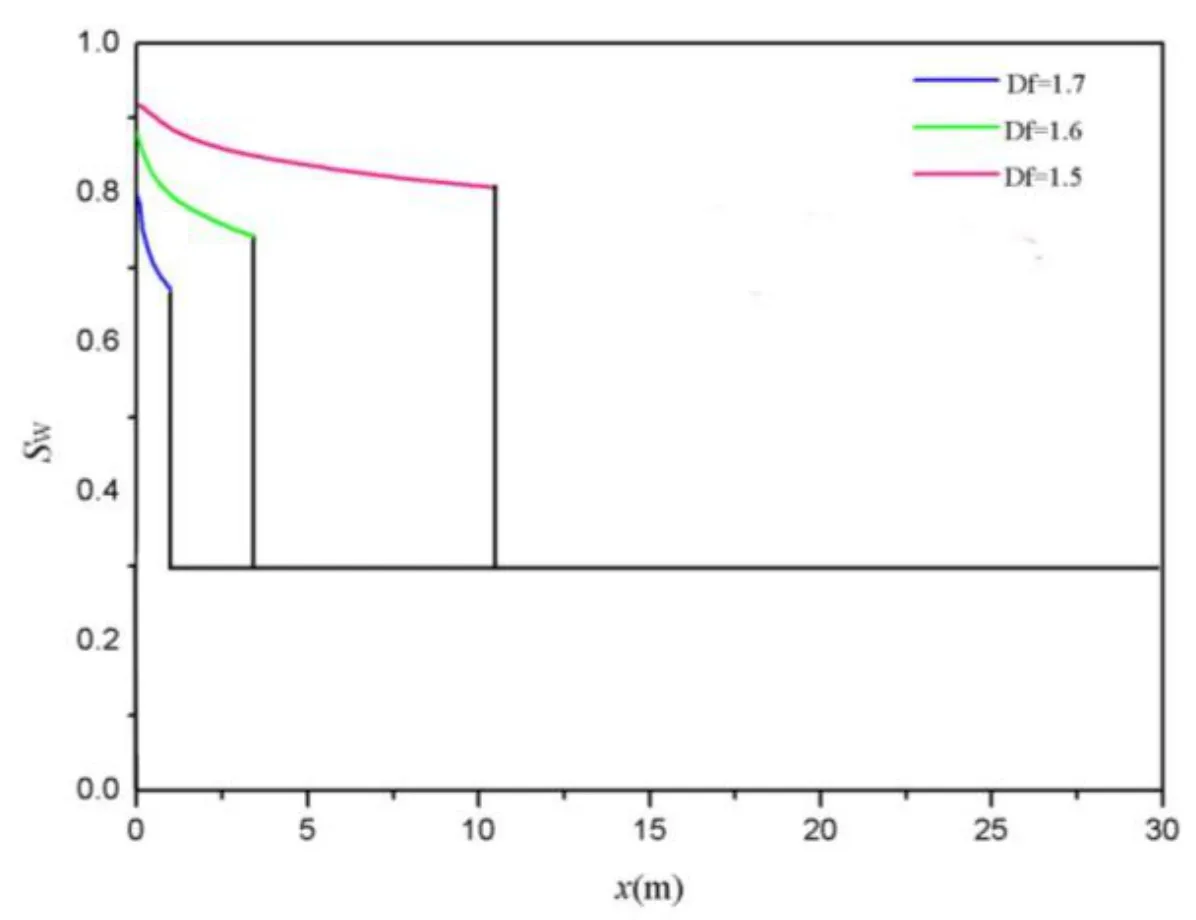
Figure 9:final water saturation profile affected by Df.(µw=1×10-3Pa.s, µo=1.2×10-3Pa.s, σ=0.06N/m, θ=0.5, L=1×10-2m,λmax=1.5×10-4m,λmin=0.2×10-7m,ΔP=5×105Pa,DT=1.14)

Figure 10:Computed water saturation profile affected by DT.

Figure 11:Final water saturation profile affected by DT.(µw=1×10-3Pa.s, µo=1.2×10-3Pa.s, σ=0.06N/m, θ=0.5, L=1×10-2m,λmax=1.5×10-4m,λmin=0.2×10-7m,ΔP=5×105Pa,Df=1.7)

Based on Eq.(41),figures12-15 show that water saturation vs.distance at different minimum pore diameter,λmin,and maximum pore diameterλmax,respectively.

For a givenλmin,fractal porous medium is better in permeability if the value ofλmaxis bigger.Because of higher value of permeability,the position of two-phase is bigger at the same water saturation with the increase ofλmaxas is shown in Fig.13.This implies it becomes more easily for water to displace oil completely with the increase ofλmax.

Similarly,fractal porous medium is better in permeability if the value ofλminis bigger.Because of higher value of permeability,the position of two-phase is bigger at the same water saturation with the increase ofλmaxas is shown in Fig.15.This implies it becomes more easily for water to displace oil completely with the increase ofλmin.

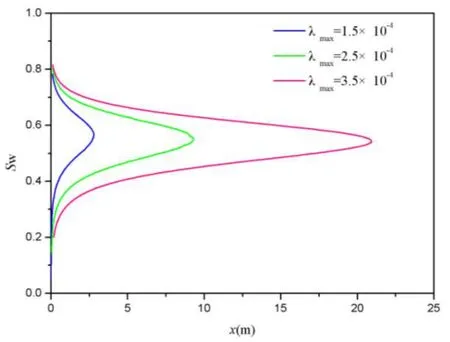
Figure 12:Computed water saturation profile affected byλmax.

Figure 13:Final water saturation profile affected byλmax.(µw=1×10-3Pa.s, µo=1.2×10-3Pa.s, σ=0.06N/m, θ=0.5, L=1×10-2m,λmin=0.2×10-7m,ΔP=5×105Pa,DT=1.14,Df=1.7).

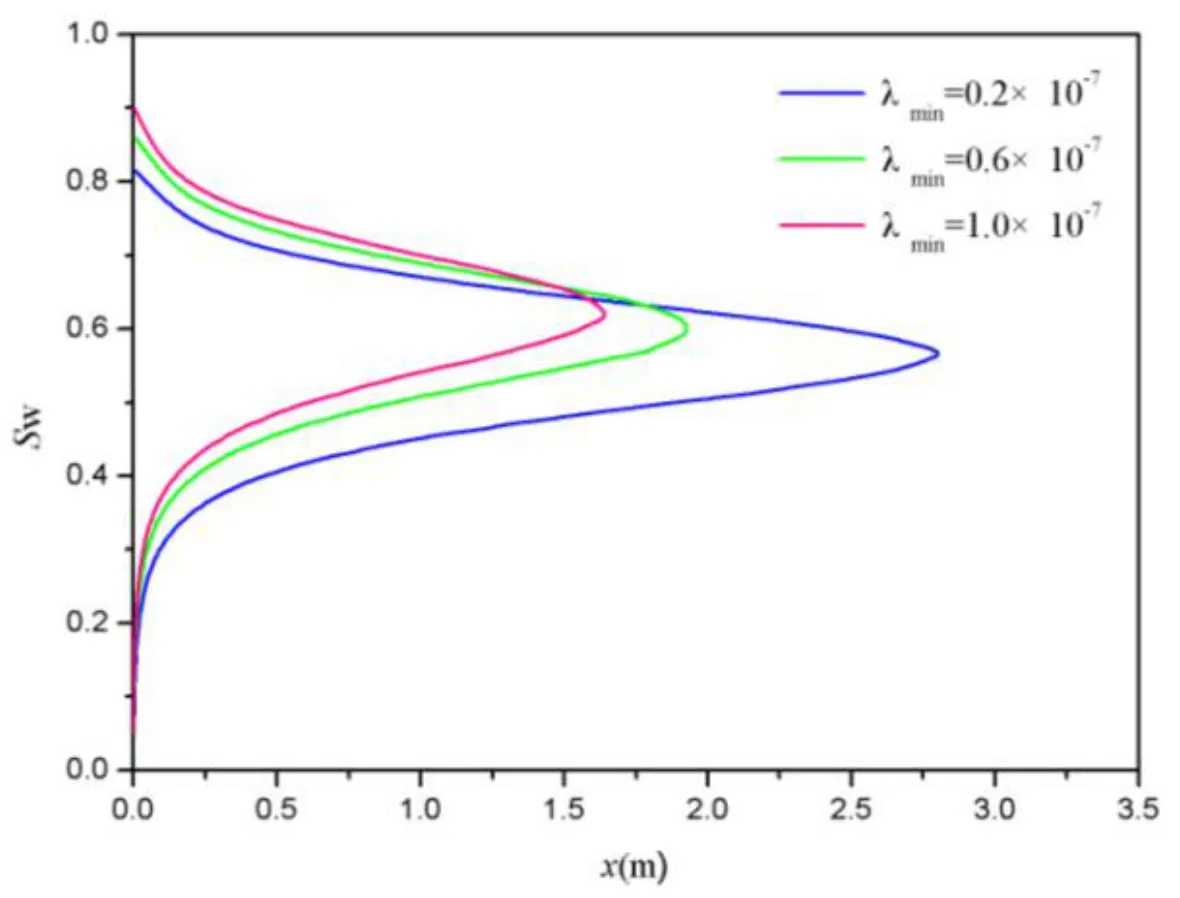
Figure 14:Computed water saturation profile affected byλmin.

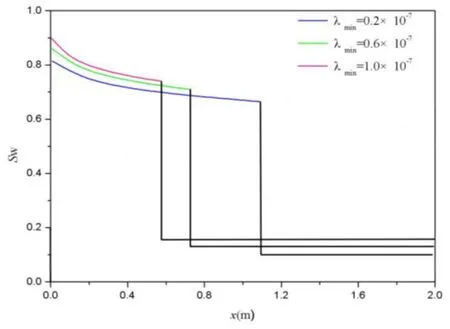
Figure 15:Final water saturation profile affected byλmin.(µw=1×10-3Pa.s, µo=1.2×10-3Pa.s, σ=0.06N/m, θ=0.5, L=1×10-2m λmax=1.5×10-4m,ΔP=5×105Pa,DT=1.14,Df=1.7).

5 Conclusions

On the approximation that a porous medium consist of a bundle of tortuous capillarieswith different diameters, we have derived a Buckley-Leverett model based onthe fractal characteristics of pore size distribution in porous medium. The proposedmodel connects any location of transient two phase flow with the structural parameters(e.g. tortuosity fractal dimension, pore fractal dimension, and maximum andminimum pore diameters) and fluid properties (e.g. interfacial tension, contact angle,viscosities and so on) of fractal porous medium In this work, we emphaticallyexhibit the process how to predict the fluid saturation profile based on fractal theoryand Buckley-Leveret analysis.

Some conclusions have been obtained as follows:

1.Based on the fractional flow model using fractal theory,we derive Buckley-Leverett solution to analyze water saturation profile for transient two-phase flow in porous medium.

2.With the increase ofDfandDT,the value of two-phase position is bigger when at the same water saturation.The permeability of porous media is better and it will take a shorter time for water to completely displace oil.

3.The permeability of porous media is better with the increase ofλmaxandλmin,the value of two-phase position is bigger at the same water saturation.It’smuch easier for water to completely displace oil.

Acknowledgement:The work is supported by Research on Key Techniques of Well Test in Deep-water Oil and Gas Reservoirs,the grant0201001009144 which is gratefully acknowledged.

Chang,J.;Yortsos,Y.C.(1992):Effect of capillary heterogeneity in Buckley-Leverett displacement.SPE(Society of Petroleum Engineers)Reservoir Engineering,vol.7,no.2,pp.3-5.

Chemetov,N.;Neves,W(2013):The Generalized Buckley–Leverett System:Solvability.Archive for Rational Mechanics and Analysis,vol.208,no.1,pp.1-24.

Cai,J.;Perfect,E.;Cheng,C.-L.;Hu,X(2014):Generalized modeling of spontaneous imbibition based on Hagen–Poiseuille flow in tortuous capillaries with variably shaped apertures.Langmuir,vol.30,no.18,pp.5142–5151.

Cai,J.C.;Luo,L.;Ye,R.(2015):Recent Advances on Fractal Modeling of Permeability for Fibrous Porous Media.Fractals,vol.23,no.1,pp.1540006.

Dongxiao,Z.;Tchelepi,H.(1999):Stochastic analysis of imm iscible two-phase flow in heterogeneous media.SPE journal,vol.4,no.4,pp.380-388.

Deinert,M.R.;Dathe,A.;Parlange,J.Y.(2008):Capillary pressure in a porous medium with distinct pore surface and pore volume fractal dimensions.Physical Review E.,vol.77,no.2,pp.021203

Frid,H.(1995).Solution to the initial boundary-value problem for the regularized Buckley-Leverett system.Acta Applicandae Mathematica,vol.38,no.3,pp.239-265.

Guzman,R.E.;Fayers,F.J.(1997):Solutions to the three-phase Buckley-Leverett problem.SPE Journal,vol.2,no.3,pp.3-7.

Katz,A.J.;Thom pson,A.H.(1985):Fractal sandstone pores:implications for conductivity and pore formation.Physical Review Letters,vol.54,no.12,pp.1325.

Kaasschieter,E.F.(1999):Solving the Buckley–Leverett equation with gravity in a heterogeneous porous medium.Computational Geosciences,vol.3,no.1,pp.23-48.

Larsen,L.;Kviljo,K..;Litlehamar,T.(1990):Estimating skin decline and relative permeabilities from cleanup effects in well-test data with Buckley-Leverett methods.SPE Formation Evaluation(Society of Petroleum Engineers)vol.5,no.4,pp.5-7.

Langtangen,H.P.;Tveito,A.;Winther,R.(1992):Instability of Buckley-Leverett flow in a heterogeneous medium.Transport in Porous Media,vol.9,no.3,pp.165-185.

Lorente,S.;Bejan,A.(2006):Heterogeneous porous medium as multiscale structures for maximum flow access.Journal of applied physics,vol.100,no.11,pp.114909

Mohsen,M.F.N.(1985):Modification of Welge’s method of shock front location in the Buckley–Leverett problem for nonzero initial condition.Society of Petroleum Engineers Journal,vol.25,no.4,pp.521-523.

Mustafiz,S.;Mousavizadegan,S.H.;Islam,M.R.(2008):Adomian decomposition of Buckley-Leverett equation with capillary effects.Petroleum Science and Technology,vol.26,no.15,pp.1796-1810.

Snyder,R.W.;Ramey,Jr.H.J.(1967):Application of Buckley-Leverett displacement theory to non communicating layered systems.Journal of Petroleum Technology,vol.19,no.11,pp.3-5.

Spanos,T.J.T.;De La Cruz,V.;Hube,J.(1986):An analysis of Buckley-Leverett theory.J.Can.Petr.Tech,vol.25,no.1,pp.71-75.

Siddiqui,S.;Hicks,P.J.;Grader,A.S.(1996):Verification of Buckley-Leverett three-phase theory using computerized tomography.Journal of Petroleum Science and Engineering,vol.15,no.1,pp.1-21.

Sumnu-Dindoruk,D.;Dindoruk,B.(2008):Analytical solution of nonisothermal Buckley-Leverett flow including tracers.SPE reservoir evaluation and engineeringvol.11,no.3,pp.555.

Terez,I.E.;Firoozabadi,A.(1999):Water injection in water-wet fractured porous media:Experiments and anew model with modified Buckley-Leverett theory.SPE Journal,vol.4,no.2,pp.134-141.

Tan,X.H.;Li,X.P.;Liu,J.Y.(2014):Analysis of permeability for transient two-phase flow in fractal porous medium.Journal of Applied Physics,vol.115,no.11,pp.113502.

Van Duijn,C.J.;Peletier,L.A.;Pop,I.S.(2007):A new class of entropy solutions of the Buckley-Leverett equation.SIAM Journal on Mathematical Analysis,vol.39,no.2,pp.507-536.

Wang,Y.;Kao,C.Y.(2013):Central schemes for the modified Buckley–Leverett equation.Journal of Computational Science,vol.4,no.1,pp.12-23.

Wang,Y.;Kao,C.Y.(2014):Bounded domain problem for the modified Buckley–Leverett equation.Journal of Dynamics and Differential Equations,vol.26,no.3,pp.607-629.

Wu,Y.S.;Pruess,K.;Chen,Z.X.(1993):Buckley-Leverett flow in composite porous media.SPEA dvanced Technology Series,vol.1,no.2,pp.36-42.

Wang,S.;Yu,B(2011):Study of the effect of capillary pressure on the permeability of porous medium embedded with a fractal-like treenet work.International Journal of Multiphase Flow,vol.37,no.5,pp.507-513.

Xiao,B.;Jiang,G.;Chen,L.(2010):A fractal study for nucleate pool boiling heat transfer of nanofluids.China Phys.Mech.Astron.,vol.53,no.1,pp.30–37.

Xu,Y.F.;Dong,P.(2004):Fractal approach to hydraulic properties in unsaturated porous medium.Chaos,Solitons&Fractals,vol.19,no.2,pp.327-337.

Xu,P.;Qiu,S.;Yu,B.;Jiang,Z(2013):Prediction of relative permeability in unsaturated porous medium with a fractal approach.Int.J.Heat Mass Transf.,vol.64,pp.829–837.

Yu,B.M.;Li,J.H.(2001):Some fractal characters of porous media.Fractals,vol.9,no.3,pp.365-372

Yu,B.M.;Chen,P.(2002):A fractal permeability model for bi-dispersed porous media.Int.J.Heat Mass Transfer,vol.45,no.14,pp.2983-2993

Yu,B.;Liu,W.(2004):Fractal analysis of permeabilities for porous medium.AIChE journal,vol.50,no.1,pp.46-57.

Young,R.(1993):Two-phase geothermal flows with conduction and the connection with Buckley-Leverett theory.Trans port in porous media,vol.12,no.3,pp.261-278.