微机电陀螺解调过程中的噪声传递机理研究

林梦娜，崔 健，刘 凯

（北京自动化控制设备研究所，北京100074）

微机电陀螺解调过程中的噪声传递机理研究

林梦娜，崔 健，刘 凯

（北京自动化控制设备研究所，北京100074）

微机电陀螺的噪声性能是衡量陀螺综合性能的重要指标之一，不仅与陀螺本身机械结构有关，还与其测控电路有着密切联系。本文将通过理论推导计算出噪声经过乘法解调和开关解调时的传递机理，指出开关解调会使解调信号中的谐波成分和解调输入噪声向解调后的基带中进行混叠，相对于纯正弦解调会增大噪声，最后应用LabVIEW软件进行纯软件仿真和半实物仿真验证，并通过实际测试数据证明其正确性，为陀螺解调方案的选择提供依据。

微机电陀螺；噪声传递；乘法解调；开关解调

0 引言

微机电（MEMS）陀螺是以微电子和微机电工艺为基础制造的惯性仪表，突出优点是成本低、体积重量功耗小、集成性高、抗恶劣环境等，在民用消费类产品、汽车电子、精确制导弹药等领域应用广泛[1-2]。

作为衡量陀螺性能的重要指标之一，很多文献分析过噪声经过运算放大器时的噪声传递，但是很少有报道分析陀螺检测模态噪声经过解调器时的传递机理。通常普遍认为在经过解调器时噪声的传递与信号的传递方式相同，即若采用单位幅值的载波信号进行乘法解调，则经过单位滤波器后，解调输出噪声的功率谱密度变为输入解调器信号噪声功率谱密度的一半；若采用开关解调，则经过单位滤波器后，解调输出噪声的功率谱密度变为解调输入噪声功率谱密度的2/π[3]。文献[4]提及在采用开关解调时，噪声以混叠的形式通过开关解调器，但理论和实践表明，开关解调时噪声的传递机制既不同于信号传递，也不是简单的叠加。因此，开展MEMS陀螺解调过程中的噪声传递机理具有重要的理论意义和工程价值。

本文将通过理论、仿真与实际测试相结合的方式研究噪声经过乘法解调和开关解调时的传递机理,为陀螺噪声性能的优化提供依据。

1 乘法解调与开关解调

含有角速率信息的检测信号经过前置差分检测放大器后，需要进行解调滤波，滤除高频信号，得到包含角速率信息的直流电压信号。解调时常采用乘法解调或开关解调[5-7]。

1.1 乘法解调

乘法解调基于乘法器的使用，如图1所示。

图1 乘法解调原理图Fig.1 Theory scheme of multiplication demodulation

假设陀螺检测信号为Acos(ωt+φ)，经过乘法器可得

经由滤波器可得

1.2 开关解调

开关解调实际上就是将信号与幅值为1V的方波信号相乘，然后通过低通滤波器，其基本原理如图2所示。

图2 开关解调原理图Fig.2 Theory scheme of switching demodulation

假设陀螺检测信号为Acos(ωt+φ)，经过解调器可得：

经由滤波器得到

2 乘法解调噪声传递分析

2.1 乘法解调噪声传递理论分析

大多数工作在载波频率处的系统，其带宽比载波频率要小，这种情况下，以正交分量和同相分量来表示噪声很方便[8]，即噪声可以表示为

其中第一项为噪声的同相分量，第二项为其正交分量，θ为任意相位。

另外可以用包络和相位分量表示噪声，即

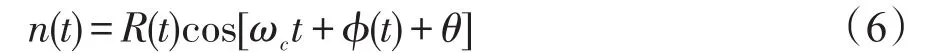
其中:

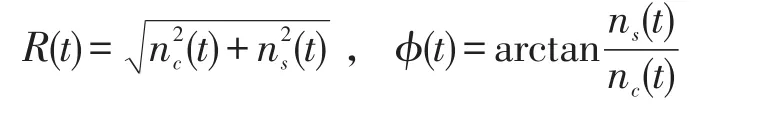
事实上，任何随机过程都可以表示为上述两种形式，但如果这个随机过程是窄带的，R(t)和ϕ(t)可以分别解释为慢变的包络和相位。

图3 产生同相分量和正交分量的步骤Fig.3 Procedure of the generation of in-phase and orthogonal components

当噪声和同相载波分量相乘后得到

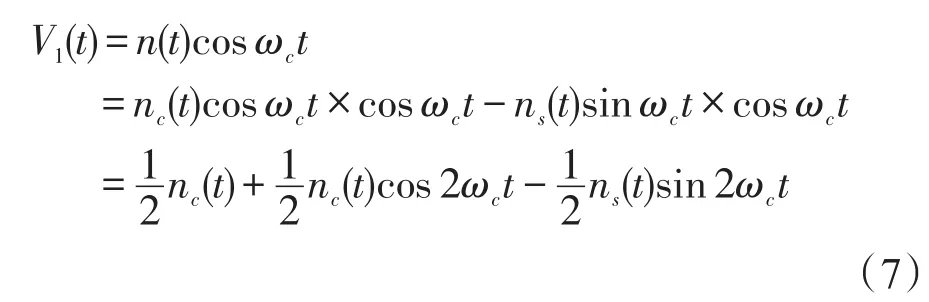
同理，当噪声和正交载波分量相乘经过低通滤波滤除高频部分后，输出只含有正交分量。

设噪声n(t)的功率谱密度(PSD)为Sn(f)，首先计算同相分量的功率谱密度函数。

由维纳-辛钦定理[49]知，功率有限信号的功率谱密度函数与其自相关函数是一对傅立叶变换，为此，先求V1(t)的自相关函数[50]。

其中，Rn(τ)为n(t)的自相关函数，设Rn(τ)的功率谱密度为Sn(f)，则由频域卷积定理[9]可得V1(t)的功率谱密度为

经过低通滤波器可得

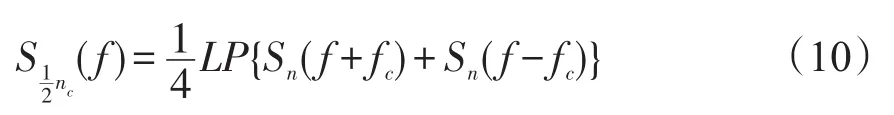
LP{}表示大括号内部信号的低通部分。

同理可得

假设噪声n(t)的功率谱密度为Sn(f)=n0，则

依据上述原理，可以推导出若噪声与信号Acosωct相乘，再经过低通滤波器，输出噪声功率谱密度为。

2.2 乘法解调噪声传递仿真分析

在分析噪声经过乘法解调器时，若应用幅值为A的正弦信号进行解调，通过单位增益的低通滤波器后，输出噪声的功率谱密度变为输入解调器的噪声功率谱密度的。若功率谱密度单位采用，则输出噪声的功率谱密度变为输入解调器的噪声功率谱密度的。

现通过纯软件仿真进行验证，仿真原理图如图4所示，功率谱密度单位采用。

图4 乘法解调噪声传递仿真Fig.4 Simulation of the noise transfer of multiplication demodulation

在LabVIEW软件中，产生一高斯白噪声，如图5所示，该噪声的功率谱密度为，分别应用幅值为1、、2的正弦波进行乘法解调，再通过单位增益、截止频率为100Hz的低通滤波器，输出信号的噪声功率谱密度如图6所示。

图5 高斯白噪声功率谱密度曲线Fig.5 PSD scheme of Gauss white noise

理论上，噪声与幅值为1的正弦波sinωt解调后输出噪声功率谱密度为，噪声与幅值为的正弦波解调后输出噪声功率谱密度为，噪声与幅值为2的正弦波2sinωt解调后输出噪声功率谱密度为，由仿真曲线可以看出，仿真值与理论计算值一致。由此验证了经过乘法解调，输出噪声的功率谱密度变为输入解调器的噪声功率谱密度的。

图6 乘法解调仿真输出曲线Fig.6 Output scheme of simulation of multiplication demodulation

同 理 ， 若 信 号 χ(t)=qsinωt+n1与 信 号y(t)=acosωt+n2相乘解调经过低通滤波器，仿真分析时，将正弦信号幅度设为q=3，噪声n1功率谱密度如图7所示。

图7 噪声n1功率谱密度Fig.7 PSD of noise n1

余弦信号幅值为a=1，噪声n2如图8所示。理论上输出信号的噪声功率谱密度经计算可以表示为，仿真得到的解调输出噪声功率谱密度如图9所示，与理论计算相符。

图8 噪声n2功率谱密度Fig.8 PSD of noise n2

图9 解调输出噪声功率谱密度Fig.9 PSD of output noise after demodulation

3 开关解调噪声传递分析

3.1 开关解调噪声传递理论分析

当应用开关解调时，解调参考信号可以看作是幅值为1的方波，噪声与方波信号相乘，解调滤波输出。由于方波信号含有不同的频率成分，如 ωd、3ωd、5ωd，这种情况比应用乘法解调要复杂得多。

依据噪声叠加理论，当各噪声源之间彼此不相关时，各独立噪声源噪声之和的均方值为各个噪声源噪声均方值之和[10]，由此可以推出，当各噪声源之间相互独立时，总噪声的功率谱密度为各独立噪声的功率谱密度之和。

噪声具有各个频率成分，且在时域上任意两个不同时刻的随机取值都是不相关的。所以，噪声各个频率成分的分量之间也是不相关的，总噪声输出功率谱密度为噪声各频率分量输出噪声功率谱密度之和。

图10 开关解调噪声传递原理图Fig.10 Theory scheme of noise transfer of switching demodulation

开关解调时噪声传递的原理图如图10所示。与方波信号解调最终能通过低通滤波器的噪声频率分量为ωd、3ωd，5ωd等，假设噪声与方波对应的基频分量为a0，3倍频分量为a3……噪声各频率分量之间相互独立。则基频分量a0与幅值为1的方波信号相乘解调，通过单位增益的低通滤波器之后，输出噪声的功率谱密度为输入解调器噪声功率谱密度的倍。假设输入解调器的噪声功率谱密度为（V2/Hz），则分量a0引起的输出噪声功率谱密度为，同理可知，a3分量引起的输出噪声功率谱密度为，依此类推，则输入解调器的总噪声引起的输出功率谱密度之和为，其中，k的取值与输入解调器的噪声带宽有关，当带宽为无穷时，上式为1。由此可见，在开关解调时，方波中的谐波成分会和输入噪声向解调后的基带中混叠。

3.2 开关解调噪声传递仿真分析

图11 开关解调仿真输出曲线Fig.11 Output scheme of simulation of switching demodulation

在LabVIEW软件中，产生一高斯白噪声，如图5所示该噪声的功率谱密度为n=1.8mV/Hz，应用幅值为1的方波解调，再通过单位增益、截止频率为100Hz的低通滤波器，输出信号的噪声功率谱密度如图11所示。理论上，开关解调后输出噪声功率谱密度为n=1.8mV/Hz，由仿真曲线可以看出，仿真值与理论计算值一致。

4 半实物仿真验证

上面仿真时采用的噪声是由软件产生，下面进行半实物仿真，采集静态下陀螺实际输出信号，也即进入解调器的信号，将采集到的信号利用软件分别进行乘法解调和开关解调。

图12 陀螺实际输出信号功率谱密度曲线Fig.12 PSD scheme of actual output signal of gyroscope

采集到的陀螺输出信号的噪声功率谱密度曲线如图12所示，噪声功率谱密度约为800nV/，理论上利用幅值为1的正弦信号进行乘法解调后输出噪声功率谱密度为，利用开关解调输出噪声功率谱密度为。采集到的信号在软件中解调后，输出噪声功率谱密度曲线如图13所示，可见理论值与仿真值很接近。

图13 半实物仿真输出曲线Fig.13 Output scheme of simulation of semi-object

5 实际测试数据

本论文采用了开关解调，现通过实际测试数据对开关解调的噪声传递机理进行验证。

采集静态下陀螺实际输出信号，即进入解调器的信号，输出信号的噪声功率谱密度曲线如图13所示，噪声功率谱密度约为800nV/Hz。后续低通滤波器增益为5.3，所以理论上低通滤波器输出噪声功率谱密度约为4μV/Hz。实际测试得到的噪声功率谱密度约为4.2μV/Hz左右，如图14所示，可以看出理论值与实测值基本一致。

图14 低通滤波输出曲线Fig.14 Output scheme of low pass filter

6 结论

本文研究了MEMS陀螺在解调过程中的噪声传递机理，分析了乘法解调和开关解调在信号和噪声传递上的差异。通过研究窄带高斯噪声同相分量和正交分量的功率谱密度，得出开关解调时的噪声混叠会使输出噪声相对于纯正弦乘法解调有所增大，并给出了纯软件仿真、半实物仿真验证，及实际测试结果，与理论相符。

后续可以利用数字解调将解调参考信号设定为幅值为1的正弦波，既解决了乘法解调中的幅度干扰问题，又避免了开关解调中的噪声混叠问题，进而提高陀螺的噪声性能。

[1]Marc S Weinberg,Anthony Kourepenis.Error sources in in-plane silicon tuning-fork MEMS gyroscope[J].Journal of microelectromechnical system,2006,15(3):479-485.

[2]V J Logeeswaran,D C K Ng,F E H Tay.A new design concept for vibrating microscope[C]//.Proc SPIE micromachining and microfabrication,2000:28-30.

[3]Erdinc Tatar.Quadrature error compensation and its ehhects on the performance of fully decoupled mems gyroscopes[D].Master thesis,Middle East Technical University,2010.

[4]Burak Eminoglu.Control electronics for mems gyroscopes and its implementation in a CMOS technology [D].Master thesis,Middle East Technical University, 2011.

[5]Ramon Casanella,Oscar Casas.Differential Synchronous Demodulator for Conductivity Sensors[J].2003: 1209-1213.

[6]Sung Woon Tahk.A novel demodulation method in MEMS gyroscope[J].Mechatronics,MEMS,and smart materials,2005.

[7]赵阳,裘安萍,施芹.微机械陀螺检测接口建模及前置放大器优化[J].光学精密工程,2013,21（7）:1734-1740.

[8]Rodger E Ziemer,William H Tranter.Principles of Communications:System,Modulations and Noise.New York:Authorized Translations of the Edition Published, 2004,291-294.

[9]郑居里.信号与系统[M].北京:高等教育出版社,1996.

[10]Reza Moghimi.Low noise signal conditioning for sensor-based circuits[J].Analog Devices,2010.

Research on Noise Transfer Mechanism of the Demodulation Operation in MEMS Gyroscope

LIN Meng-na,CUI Jian,LIU Kai
（Beijing Institute ofAutomatic Control Equipment,Beijing 100074,China）

The noise performance of the gyroscope is one of the most important factors of the performance of MEMS gyroscope.It is not only related with the mechanical structure,but also has an intimate connection with the circuits.This paper carries a comprehensive derivation on the noise transfer of the demodulation operation.The work compares the differences on noise transfer between multiplication demodulator and switching demodulator by decomposing the narrowband Gaussian noise into the in-phase and orthogonal components.The results show that the noise located in the harmonic components of the carrier can be folded into the base band through the switching demodulator,increasing the noise compared to the pure sinusoid multiplication demodulation,which is verified via simulation and experiments.

MEMS gyroscope;Noise transfer;Multiplication demodulation;Switching demodulation

V444

A

2095-8110（2015）02-0039-07

2014-11-18；

2015-01-12。

林梦娜（1988-），女，硕士，助理工程师，主要从事微机电陀螺方面的研究。E-mail:lmn-58@126.com