基于IMM理论的大型舰船被动定位算法研究
刘朝阳,杨 军,朱学平,袁 博
(西北工业大学航天学院,西安710072)
基于IMM理论的大型舰船被动定位算法研究
刘朝阳,杨 军,朱学平,袁 博
(西北工业大学航天学院,西安710072)
针对相控阵导引头跟踪航母等大型舰船目标的要求,为了给雷达成像进行运动补偿、给目标识别提供更多的先验信息,必须对目标运动参数进行准确的估计,但是常规被动定位算法通常采用单一目标运动模型,难以适应大型军舰运动规律的多样化,导致模型不匹配,使得误差较大,难以对目标参数进行准确估计,为解决上述问题,提出了一种基于交互式多模型(IMM)理论的大型舰船被动定位方法,使用不同的模型来匹配舰船不同的运动状态。仿真结果表明,提出的方法与常规的被动定位算法相比,定位精度明显提高,且易于工程实现。
大型舰船;被动定位;交互式多模型;卡尔曼滤波
0 引言
早在二战前,目标定位技术就已经在军事上得到应用。1937年世界上出现了第一部跟踪雷达站SCR-28。之后,随着科技的进步,各种跟踪系统相继出现并不断完善,跟踪理论和方法在各国学者的努力下也获得了很大的发展。比如扩展卡尔曼滤波、粒子滤波、多模型、多速率处理等,结合这些技术提出了许多方法,取得了很大的进步。
机动目标的运动模型问题,国内外进行了许多研究,取得了一些成果:1969年R.A.singer提出了Singer模型[1],将目标的机动加速度表示为随机状态噪声的结果,并由此建立起机动目标运动的统计模型。1979年,R.L.Moose等人提出了具有随机开关均值的半马尔可夫机动目标统计模型[2]。1983年,我国学者周宏仁提出了机动目标的“当前”统计模型[3]。然而,Singer模型较为粗糙,对机动目标的跟踪效果相对较差。“当前”统计模型虽然能够实时地给出目标状态的正确估计,但其依赖于一些目标的先验信息,如最大加速度等。这几种方法都只对相应的机动模型有较好的效果。
然而大型军舰运动模式主要包括:定常速度模式、定常加速度模式、定常回转运动模式,且各种运动模式的出现和改变是随机的。这样由于目标运动模型不匹配,会导致较大的定位误差,甚至是滤波的发散。
鉴于以上原因,本文根据交互式多模型(IMM)理论,使用多个不同的运动模型分别匹配目标的不同运动状态,首先建立大型舰船定常速度状态方程、定常加速度状态方程、定常回转运动状态方程,目标状态的估计及模型概率的更新使用扩展卡尔曼滤波和马尔科夫链。仿真结果表明:基于IMM理论的大型舰船被动定位算法的估计精度远高于常规被动定位算法。
1 被动定位问题数学模型的描述
1.1 大型舰船运动分析
当前大型军用舰船主要包括航空母舰、巡洋舰、导弹驱逐舰等。针对大型舰船被动定位技术开展研究,有必要对典型大型军舰的运动情况进行分析并建立相应数学模型。
大型军用舰船属于慢速移动目标,主要包括直航运动、返航运动和转弯运动等运动状态,其运动情况可归纳为以下三种:
1)直航运动,舰船在水面上巡航阶段,属于匀速直线运动,航速15m/s;
2)加速运动,舰船由初速度为9m/s的巡航速度加速到全速前进阶段,加速度一般很小,约为0.14m/s2;
3)转弯运动,舰船的转弯运动一般为定常回转运动。定常回转直径与舰船本身的长度有关,对于大型军舰定常回转直径与舰长的比值为3~10。向心加速度取为0.01m/s2。
1.2 状态方程的建立
1.2.1定常速度模型
大型舰船的直航运动主要是慢速的匀速直线运动,可采用定常速度模型来描述,选取状态变量为
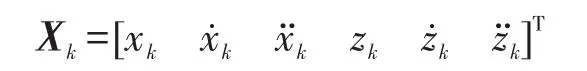
状态方程可写为
式中ωk=[ωχ(k) ωz(k)]T为二维高斯白噪声。1.2.2定常回转运动模型
令
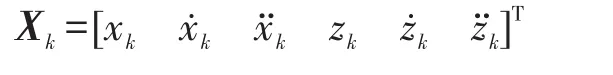
状态方程可写为

由于转弯速率未知,因此可利用最近两次状态估计的速度分量做如下估计,即:
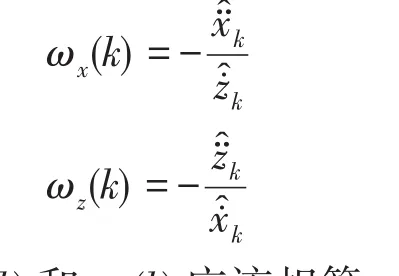
理论上,ωχ(k)和ωz(k)应该相等,即为目标在水平面内的转弯速率,实际上ωχ(k)和ωz(k)一般不等,因此建议使用ω(k)=max{ } |ωχ(k)|,|ωz(k)|。1.2.3定常加速度模型
当目标作常加速运动时,令
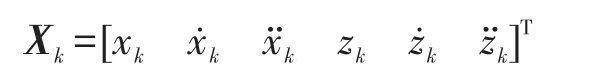
状态方程可写为
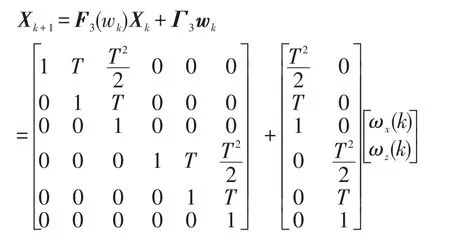
ωk=[ωχ(k) ωz(k)]T为二维高斯白噪声。
1.3 观测方程的建立
发射坐标系中目标-导弹相对运动关系如图1所示。
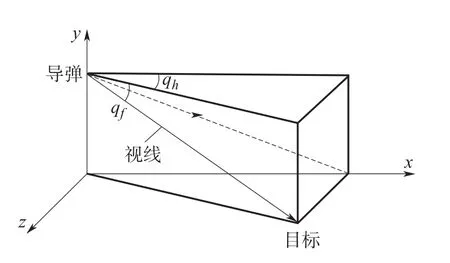
图1 目标-导弹相对运动关系示意图Fig.1 The schematic diagram of relative motion
由目标-导弹相对运动关系,给出目标视线高低角和视线方位角的计算公式[5]:
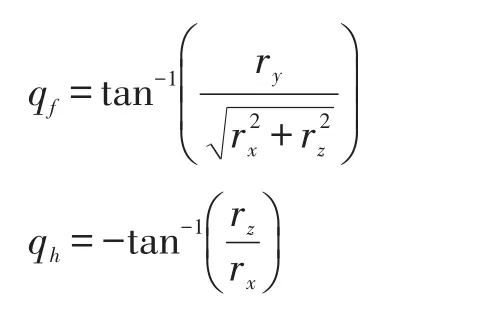
目标的视线角无法通过导引头直接测量,直接测量到的导引头俯仰框架角和偏航框架角,即弹体系视线角,而被动定位算法的观测量选取为导弹与目标惯性系的相对距离。如何建立在不同坐标系下状态变量与观测量之间的关系是首先需要考虑的问题。
通常的做法是将惯性系相对距离由惯性坐标系到弹体坐标系的转换矩阵转换至弹体系后,再由视线角的计算方法给出框架角,即弹体系视线角。具体方法如下:

由此可将观测方程建立如下

其中z(k)为观测量,选取为导引头框架角,h(X (k))为非线性函数,v(k)为测角噪声。
求取h[X(k)]的线性化矩阵H
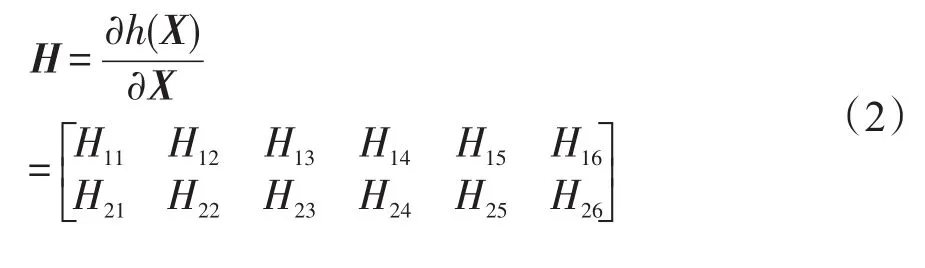
2 基于IMM理论的大型舰船被动定位技术研究
由于舰船运动状态的不确定性,采用单一的机动目标数学模型难以完成对军舰的定位定速,因此本文采用基于交互式多模型(IMM)的推广卡尔曼滤波算法,使用不同的模型来匹配不同的运动状态,这样就克服了使用单一模型时目标状态与模型不符合引起的误差。
2.1 推广卡尔曼滤波(EKF)算法[6]
将导弹-目标运动非线性模型建立如下:
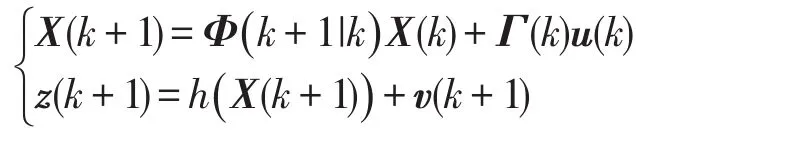
式中:Φ为状态转移矩阵,Γ为状态方程的输入控制矩阵,T为采样时间,u为状态方程输入,z为观测量,v为观测噪声,h(X)为非线性函数。
EKF算法可写为:
预测方程
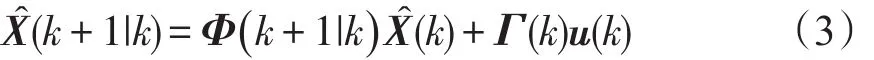
预测协方差
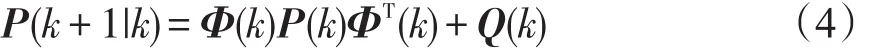
卡尔曼增益
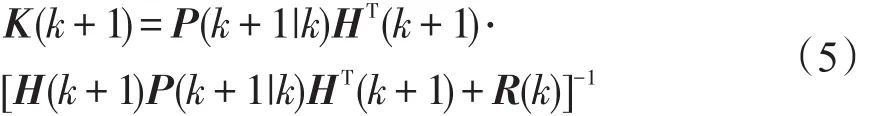
滤波方程为
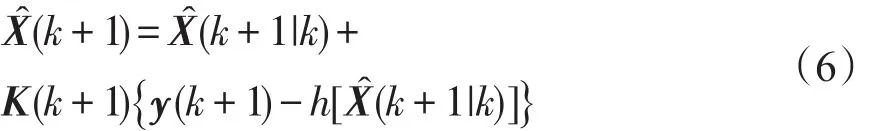
估计误差协方差为
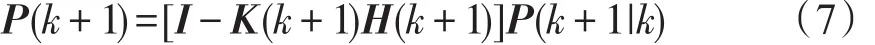
算法初值选取:
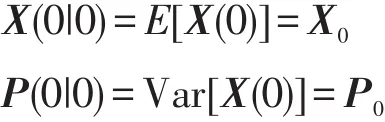
则采用由式(3)~式(7)组成推广卡尔曼滤波算法,可以得到系统状态的最优估值。
2.2 交互式多模型(IMM)算法
由于舰船运动状态的不确定性,需要使用不同的模型来匹配不同的运动状态,因此采用交互式多模型(IMM)算法,就克服了使用单一模型时目标状态与模型不符合引起的误差。
各种运动模型间的转换使用马尔科夫链,算法原理图如下所示:
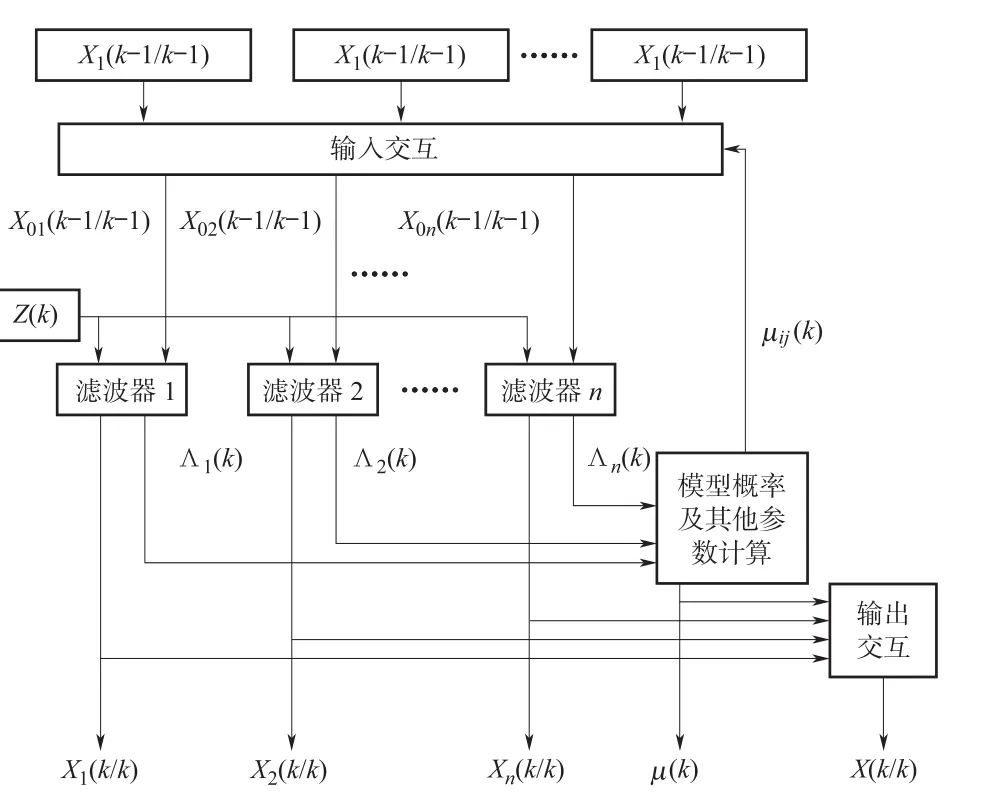
图2 IMM算法原理图Fig.2 The scheme of IMM
在该问题中建立了描述目标直航运动、定常回转运动和定常加速度运动的数学模型,其离散状态方程如下
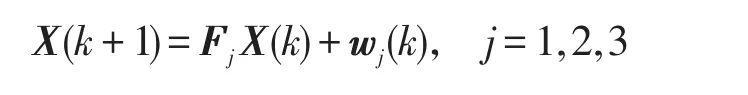
其中,Fj是模型 j的状态转移矩阵,wj(k)是均值为0,协方差矩阵为Qj的离散时间白噪声序列,即状态噪声。
观测方程为
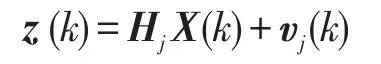
式中,Hj为模型 j的观测矩阵,v(k)是均值为0,协方差矩阵为R的离散时间白噪声序列,即观测噪声。
马尔科夫转移概率矩阵为:
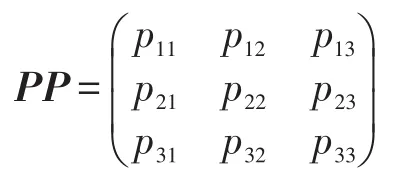
其中, pij为从模型i转移到模型 j的转移概率。
一般而言,经典的IMM算法的一个递推循环由以下三步组成:
1)输入交互
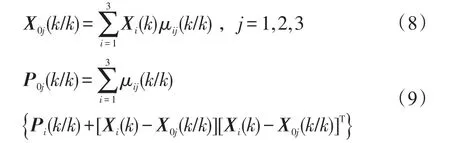
其中 μij(k/k)=pijμi(k)/
上式中
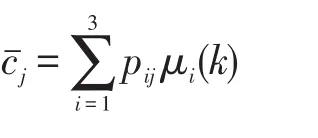
2)对应于模型 j,进行卡尔曼滤波
状态预测值

状态预测误差协方差为
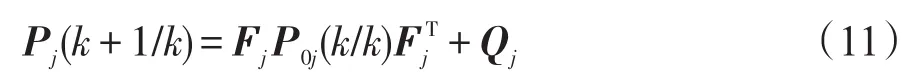
卡尔曼增益为
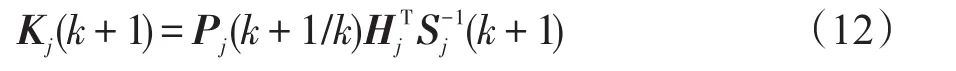
k+1时刻的滤波值为
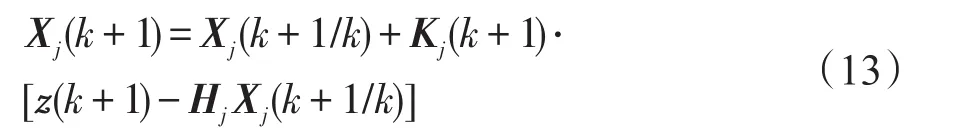
滤波协方差为
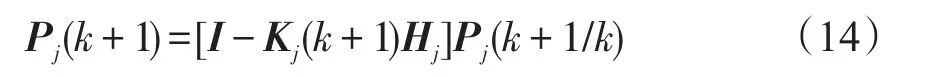
模型概率更新
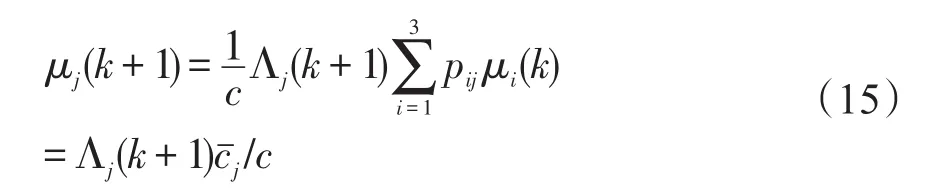
以上各式中
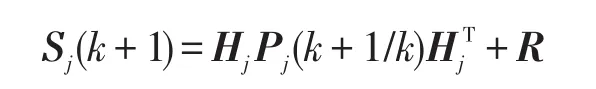
c为归一化常数,且
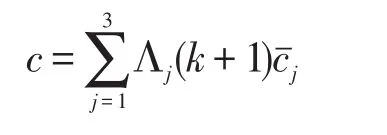
而Λj(k+1)为观测量z(k+1)的似然函数
上式中,γj(k+1)为信息,且
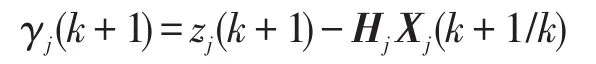
3)输出交互
3 仿真验证
采用基于IMM理论的推广卡尔曼滤波方法与采用定常速度模型的推广卡尔曼滤波方法在同一条件下进行对比仿真分析,仿真条件为目标初始位 置 (0m,0m,0m), 导 弹 初 始 位 置(8041m,4889m,-5.6m)。目标首先做初速度9m/s,加速度0.1m/s2的匀加速直线运动,当加速到15m/s时开始直航运动,150s时开始转弯,转弯角速度为0.0083rad/s,单次仿真结果如图3~图10所示。
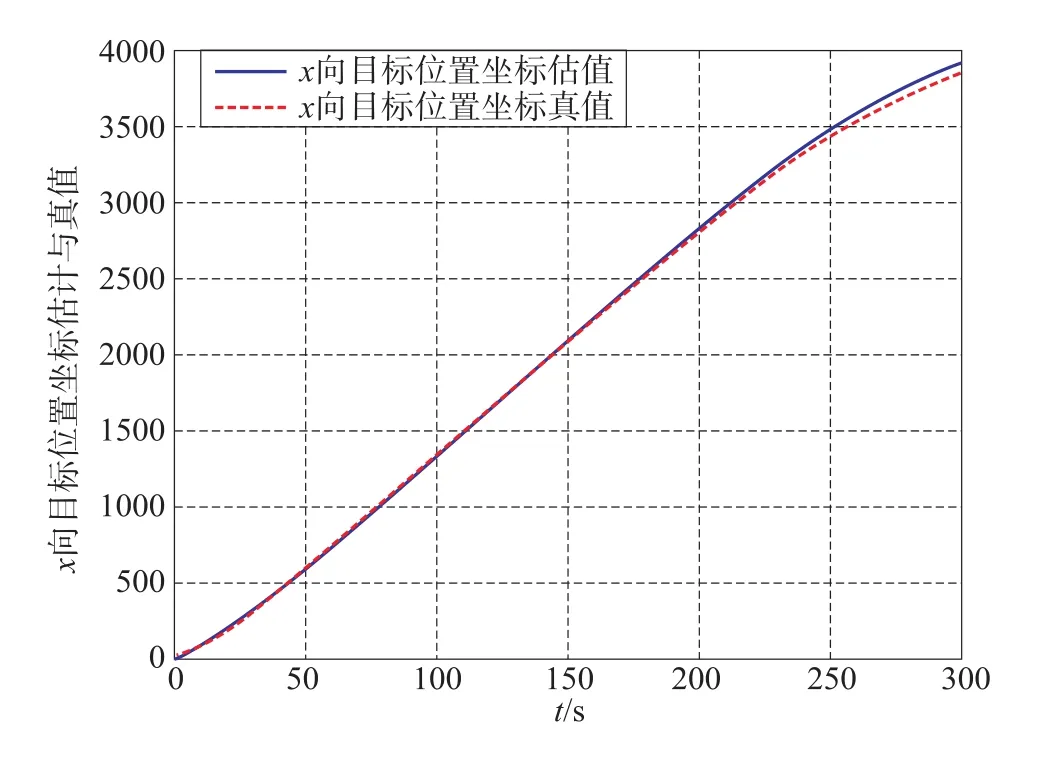
图3 χ方向位置坐标估计与真值—多模型Fig.3 The schematic diagram of position χ-Multi-model
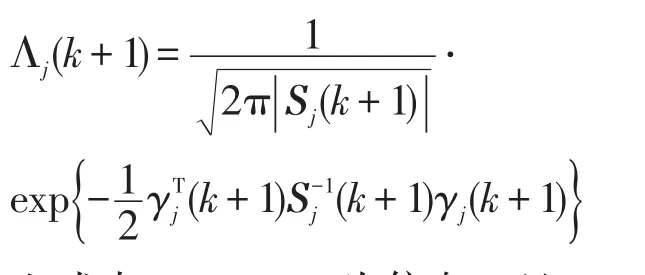
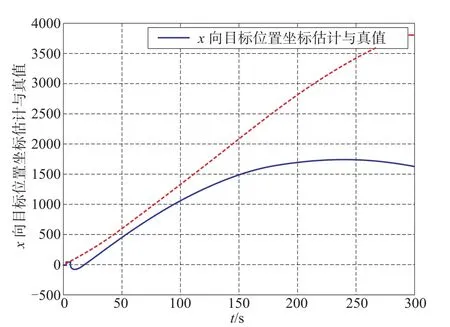
图4 χ方向位置坐标估计与真值—单模型Fig.4 The schematic diagram of position χ-Single-model
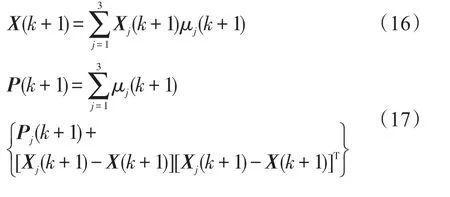
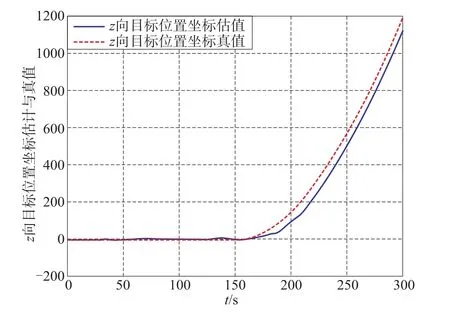
图5 z方向位置坐标估计与真值—多模型Fig.5 The schematic diagram of position z-Multi-model
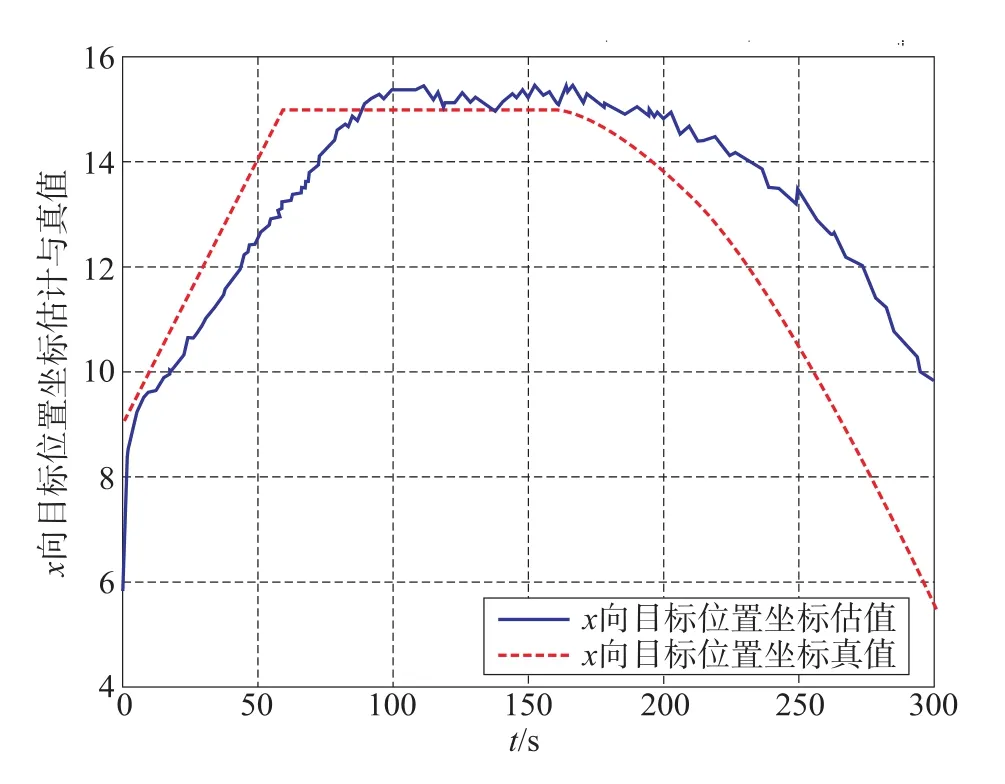
图7 χ方向速度估计与真值—多模型Fig.7 The schematic diagram of speed χ-Multi-model
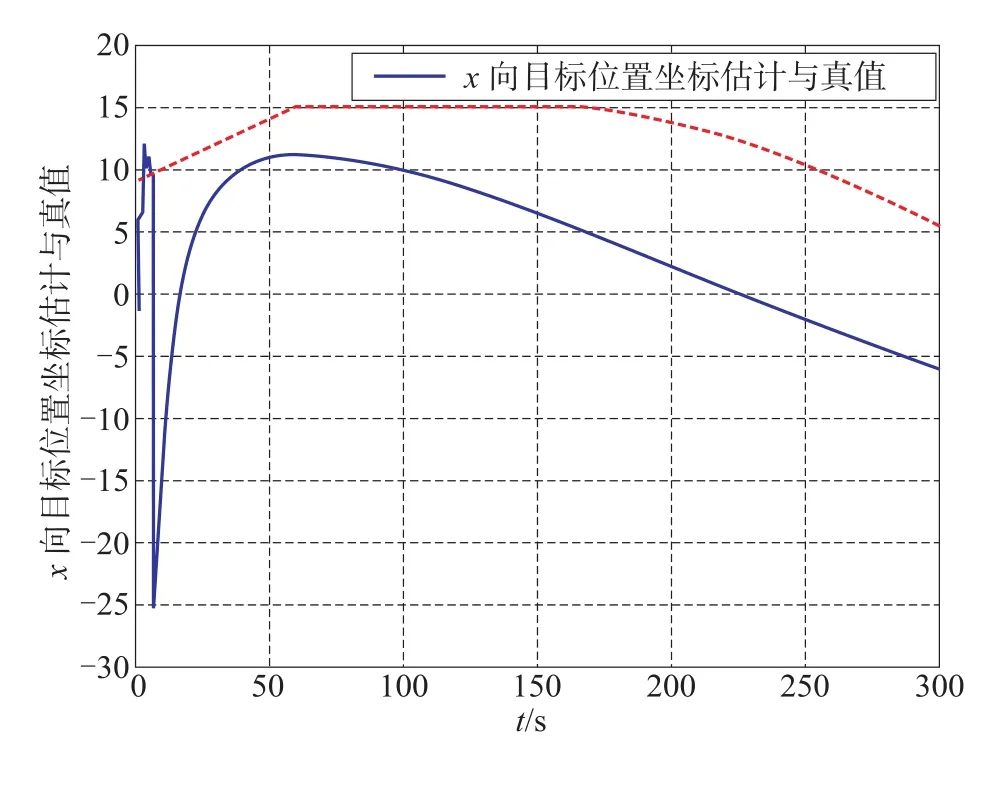
图8 χ方向速度估计与真值—单模型Fig.8 The schematic diagram of speed χ-Single-model
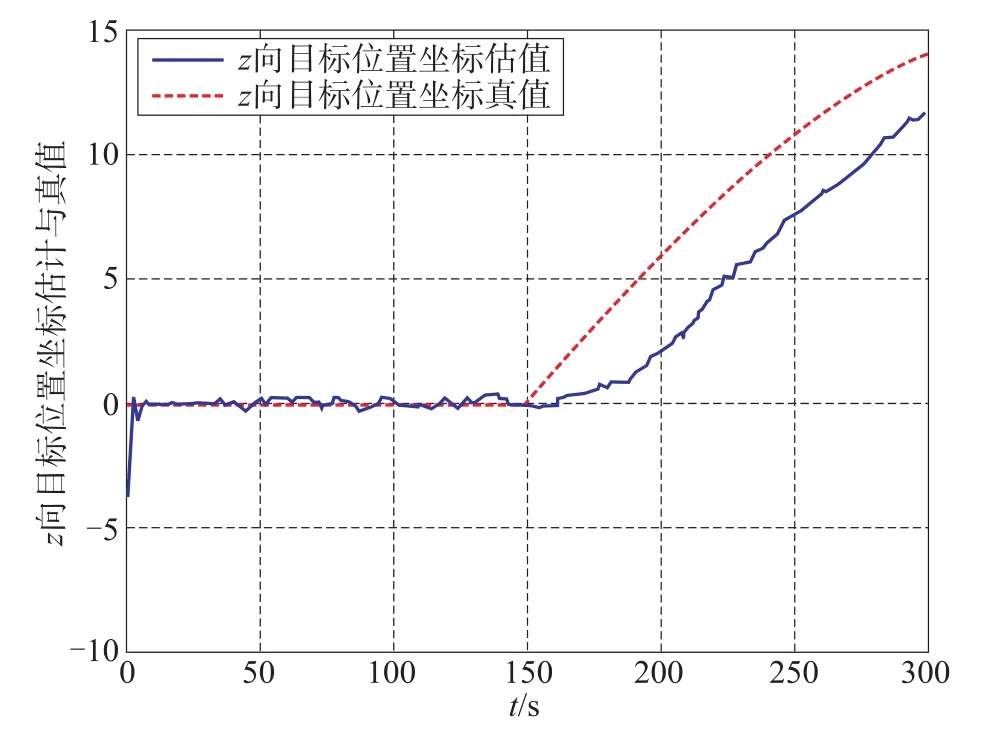
图9 z方向速度估计与真值—多模型Fig.9 The schematic diagram of speed z-Multi-model
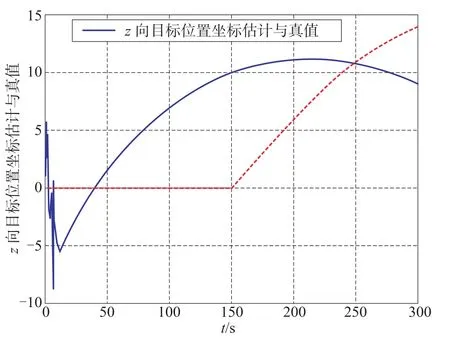
图10 z方向速度估计与真值—单模型Fig.10 The schematic diagram of speed z-Single-model
由仿真结果可以看出本文提出的基于IMM理论的大型舰船被动定位方法的定位定速误差明显小于单一模型的EKF算法。通过200次随机仿真对本文提出的方法进行仿真分析,仿真条件与单次仿真相同,结果如表1所示。
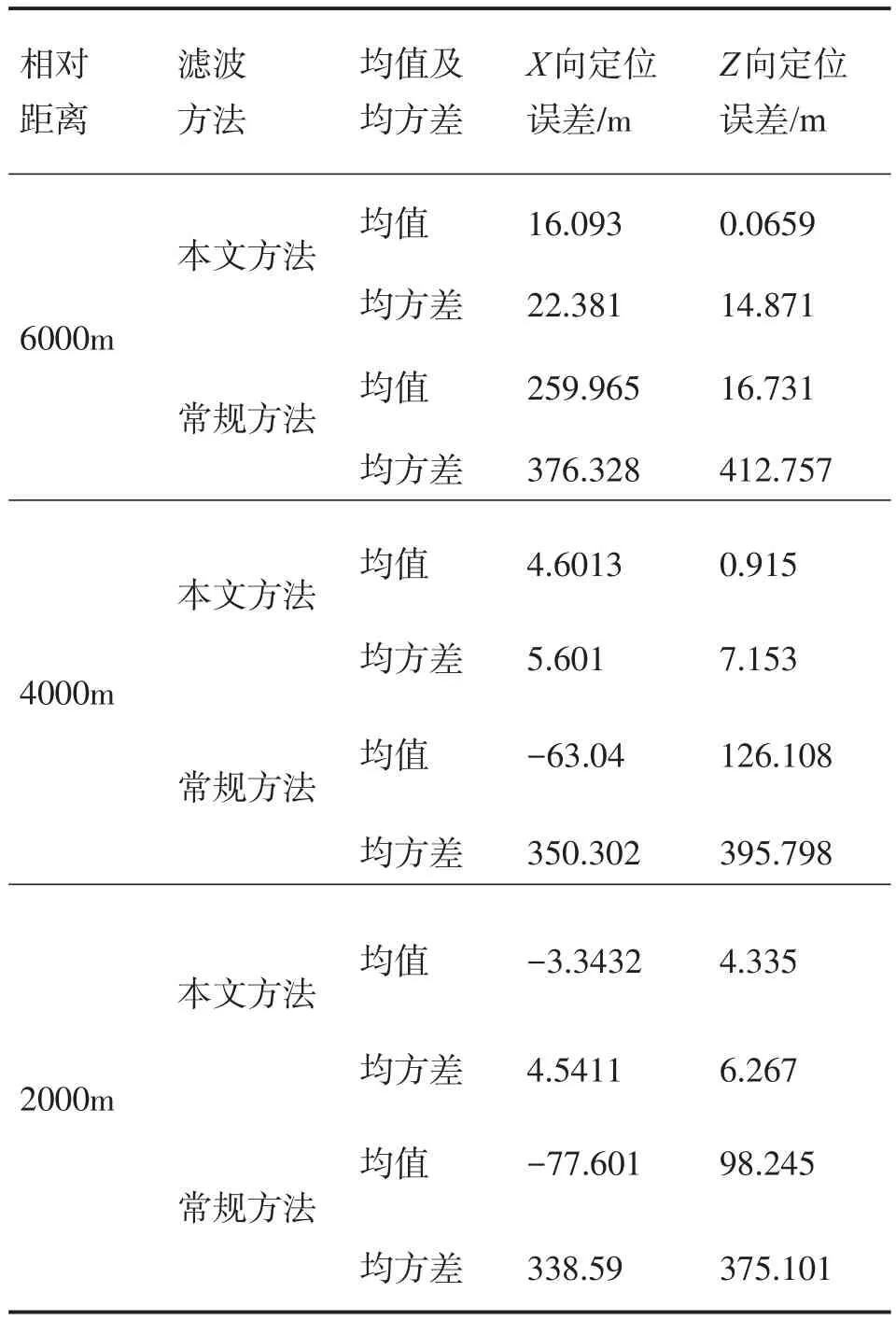
表1 被动定位精度对比分析Tab.1 The accuracy comparison of passive location
4 结论
由以上分析结果可以看出,常规的EKF算法因未考虑大型军舰多种运动模式的影响,估计精度误差较大。本文通过交互式多模型算法,建立了大型军舰的定常速度状态方程,定常加速度状态方程,定常回转运动状态方程,考虑了大型军舰的多种运动模式,使得滤波精度大大提高。基于IMM算法的被动定位滤波算法,在相同的弹目距离时,各方向定位误差均值和均方差均远小于常规EKF滤波算法,且具有较高的估计精度。
[1]Singer R A.Estimating optimal tracking filter performance for manned Maneuvering targets[C]//.IEEE Transactions on Aerospace and Electronic Systems, 1970,Vol.AES-6,No.4:473-483.
[2]Moose R L,Vanlandingham H F,McCabe D H.Modeling and estimation for tracking maneuvering targets[C]//. IEEE Transactions on Aerospace and Electronic Systems,1979,Vol.AES-15,No.3:448-456.
[3]周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1991.
[4]潘泉.机动目标自适应算法研究[D].西安:西安科学大学,1999:46-60.
[5]李新国,方群.有翼导弹飞行力学[M].西北工业大学出版社,2008.
[6]周凤岐,卢晓东.最优控制理论[M].北京:高等教育出版社,2009.
The Large Warship’s Passive LocationAlgorithm Based on IMM
LIU Zhao-yang,YANG Jun,ZHU Xue-ping,YUAN Bo
(School ofAstronautics,Northwestern Polytechnical University,Xi'an 710072,China)
According to the phased array radar seeker tracking aircraft carriers and other large ships,in order to give motion-compensated signals and provide more informations,the phased array radar seeker has to estimate the target information.However,the conventional passive location algorithm usually uses single target model,which is difficult to adapt the target’s different mobilities.It usually results in model mismatch and larger positioning error.In order to solve the above problems,in this paper,the large warship’s passive location algorithm based on IMM is proposed,which uses different models to match different ship motion states.The simulation results show that this method can give higher positioning accuracy and is easy to achieve.
Large warship;Passive location;IMM;Kalman filter
TJ765.4
A
2095-8110(2015)02-0020-07
2014-12-24;
2015-01-09。
刘朝阳(1989-),男,硕士,主要研究领域为导航制导与控制。E-mail:429720052@qq.com

