基于有向图的航天器编队飞行自适应姿态协同控制

党宏涛，伊国兴，李清华

（1.哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨150001；2.解放军96117部队，山东莱芜 271100）

基于有向图的航天器编队飞行自适应姿态协同控制

党宏涛1,2，伊国兴1，李清华1

（1.哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨150001；2.解放军96117部队，山东莱芜 271100）

在有向通信拓扑下研究了编队航天器自适应姿态协同控制问题。针对航天器编队飞行系统中存在外部扰动和模型不确定性的情况，通过选取包含相对姿态误差和绝对姿态误差的辅助变量，提出了一种鲁棒自适应控制策略。提出了自适应律估计转动惯量矩阵和扰动上界等未知参数，并且利用Lyapunov稳定性理论分析了闭环系统的渐近稳定性。与滑模控制等传统鲁棒控制不同，所设计的鲁棒自适应控制器是连续的，更便于航天器编队飞行系统的实现。最后通过仿真验证了该控制策略能够实现高精度的编队飞行跟踪控制。

编队飞行；有向图；协同控制；渐近稳定；自适应律

0 引言

航天器编队飞行指利用多个飞行中的航天器组成具有一定编队构形的系统，各颗航天器之间通过星间通信相互联系、进行协同工作。和传统单颗航天器相比，它具有灵活性强、可靠性高、成本低等优点，同时能完成更复杂的空间任务。进行有效的姿态协同控制是实现高精度的航天器编队飞行任务的基本条件之一[1-5]，因此需要对各颗编队航天器设计姿态协同控制策略。

Lawton等[6]研究了分布式深空干涉仪的姿态协同控制问题，基于一致性算法和行为控制的思想，在航天器跟踪定常的外部信号进行姿态机动时，保证航天器成员的相对姿态的一致性。随后在文献[7]中，Lawton等进一步提出了基于系统无源性的姿态协同控制方法，在通信拓扑为无向环形图的情况下证明了系统的局部渐近稳定性。针对期望角速度等外部信号为时变的情形，VanDyke等[1]提出了含有绝对姿态跟踪和相对姿态保持的分布式协同控制器，利用Barbalat引理证明了闭环系统的渐近稳定性，且航天器通信拓扑只需要为无向图。Ren等[2,5]利用一致性算法的思想，对期望的外界姿态跟踪参考信号全局已知、仅部分航天器已知期望参考信号的情况，分别设计了航天器姿态协同控制算法。值得指出的是，文献[2,5]将通信拓扑从无向图推广到了有向图的情况。Wu等[8]采用滑模控制设计方法，在参数不确定性和外界干扰的情况下，设计了基于有向图的姿态同步跟踪控制算法。但是文献[8]中的控制器需要相邻航天器的控制力矩信息，只能适用于特殊的通信拓扑结构。张海博等[9]同样在参数不确定性和外界干扰的情况下，基于有向图设计了鲁棒自适应姿态协同控制，但是控制器中含有符号函数，可能导致“抖振”现象。

但是文献[1-7]并没有同时考虑有向通信拓扑、外界扰动和内部的参数不确定性。文献[8-9]虽然考虑了有向通信拓扑、外界扰动和内部的参数不确定性，但是对于航天器执行机构为飞轮或控制力矩陀螺等连续输入的情况，所设计的滑模控制难以直接应用于航天器编队飞行系统中。针对以上不足，本文给出了连续的分布式自适应鲁棒姿态协同控制策略，同时控制器对于未知外界扰动和内部的参数不确定性具有鲁棒性。特别地，和传统的非连续控制策略如滑模控制[8-9]相比，本文提出的连续鲁棒姿态协同控制器具有更好的工程应用性。

针对航天器编队飞行系统，本文提出了有向通信拓扑结构下的鲁棒自适应姿态协同控制策略。考虑到外部扰动和航天器转动惯量不确定性的情况，利用自适应控制理论设计了自适应律，估计外部扰动的上界和航天器转动惯量，提出了一种鲁棒自适应控制器，并且分析了闭环系统的渐近稳定性。最后数值仿真验证了所提出的鲁棒自适应控制器的有效性。

1 基础理论

1.1 编队航天器姿态协同控制模型

本文考虑n个航天器的姿态协同控制问题，采用MRPs描述的编队航天器i的姿态动力学和运动学方程为[9]：

其中，Ji∈R3×3表示第i个航天器的转动惯量矩阵；ωi∈R3为体坐标系下的角速度；τi∈R3和di∈R3分别表示控制力矩和扰动力矩。σi∈R3表示航天器相对惯性坐标系的姿态在本体系下的投影。对于任意的向量ξ=[ξ1ξ2ξ3]T，ξ×表示由ξ生成的如下反对称矩阵：

且G(σi)满足以下性质：

设期望的角速度为ωd∈R3，期望的姿态定义姿态误差和角速度误差分别为：

其中

为姿态变换的旋转矩阵，本文中简记为C。由式（1）、式（2）、式（7）和式（8）可得航天器姿态误差模型为：

下面给出转动惯量矩阵Ji和外界扰动di的假设：

假设1：航天器转动惯量矩阵Ji为未知的正定矩阵，扰动力矩di是有界的满足‖di‖∞≤，其中>0为未知常数。

本文的目的即为，设计控制器τi，使得当t→∞时，˜→I3，→0。

1.2 代数图论

本文主要利用有向图描述航天器之间的信息交互。记有向图为G=(υ,ς,C)，它由节点集υ={υ1,υ2,…,υn}、边集ς⊆υ×υ和加权邻接矩阵C=[cij]∈Rn×n组成[2]。如果节点υi能直接获取节点υj的信息，那么图中就有一条边从υi指向υj，记作(υi,υj)∈ς。图G的加权邻接矩阵C中的元素定义为：当(υi,υj)∈ς时，cij>0；否则，cij=0。一般假设节点与自身没有连通性，即cii=0。图的路径为一个有限的节点序列υ1,…,υk，对于任意的1≤i≤k-1，满足(υi,υi+1)∈ς。如果有向图中除了一个根节点外，其余每个节点有且仅有一个父节点，且存在根节点到其他任何节点的路径，则称此有向图为有向树。有向图的有向生成树指包含此有向图的所有节点的有向树。如果有向图存在一个为有向生成树的子图，则称其具有有向生成树。对于航天器的信息交互，有如下假设：

假设2：航天器之间的通信拓扑图G具有一个有向生成树。

定义有向图G的Laplacian矩阵为

引理1[10]：如果有向图G具有有向生成树，则L由且仅有一个特征值为零，并且其余特征值位于虚轴的右半平面。

2 控制器设计

在本节中，假设编队中的航天器均能够获得期望角速度和角加速度信息，且期望的角速度ωd和角加速度ω.d是有界的。控制目标为在航天器存在转动惯量不确定性和外界干扰的情况下，设计鲁棒自适应姿态协同跟踪控制器，使得航天器的姿态达到协同，同时跟踪期望的姿态和角速度。首先给出下面的假设和引理。

引理2[11]：对于任意的实数χ和非零实数y，下面不等式成立

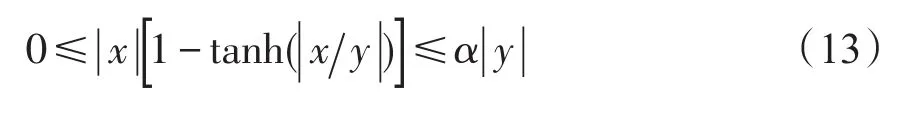
其 中 α>0 ， 其 最 小 值 α*满 足α*=χ*(1-tanhχ*)，χ*满足方程e-2χ*+1-2χ*=0。

受文献[12]启发，定义辅助误差变量为

其中常数ki>0，ei为航天器姿态协同误差向量，定义为

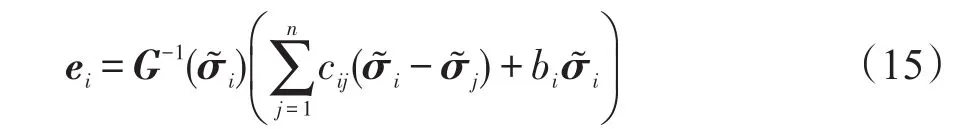
其中常数bi>0。由式（10）和式（14），可得

记第i颗航天器的转动惯量矩阵为

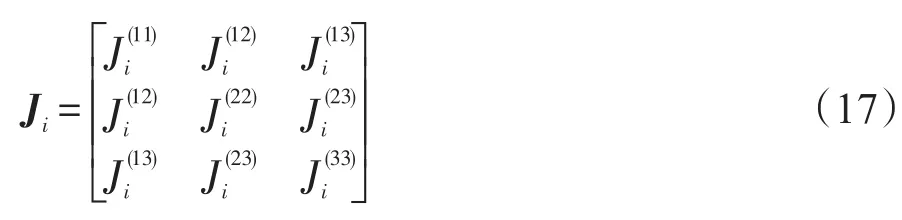
则第i颗航天器的自适应参数记为

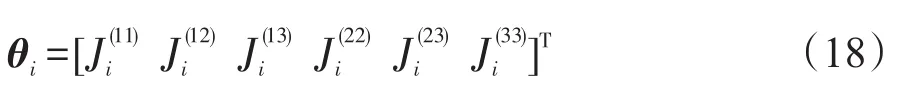
对于向量y=[y1y2y3]T，定义线性算子T1:R3×1→R3×6和T2:R3×1→R3×6为：

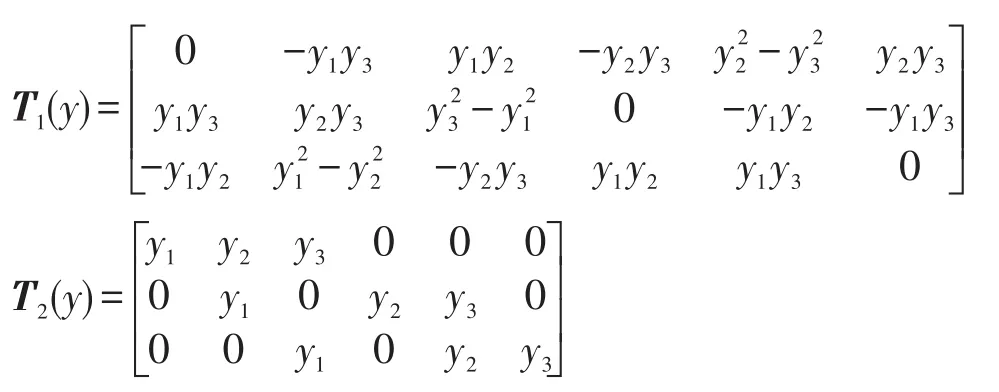
定理1：考虑在控制器（20）～（23）作用下的航天器编队姿态跟踪误差系统（10）～（11），如果假设1和假设2成立，则当 t→∞时，→0，→0(i=1,…,n)。

证：引理2中的不等式（13）可以写为

对式（26）求导，并利用式（19）～式（23），可得

把控制器（20）代入式（27）可得，

由式（25）和式（28），可得

由于ki>0，因此V.≤0，从而V是有界的，并且 si,。由式（19）和式（20）可得，∈L∞，并且从式（29）可得 si∈L2，因此利用Barbalat引理[13]可得，当t→∞时，si→0。

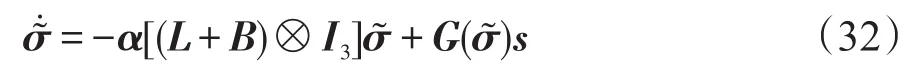
由于本文假设航天器之间信息交互拓扑图具有一个有向生成树，因此由引理1可得，L有且仅有一个特征值为零，并且其余特征值位于虚轴的右半平面，并且rank(L)=n-1。由于每一个bi均大于0，因此rank(B+L)=n，且所有特征值均大于0，同时由α是正定矩阵，可得-α((L+B)⊗I3)是Hurwitz矩阵。注意到s∈L2⋂L∞，根据定理4.9.1[14]，将s视为系统输入，˜为系统状态，则系统（32）是渐近稳定的，因此可得当t→∞时，˜→0。由于已经证得 s→0，因此由式 （31） 可得，→0。由此可得，对于任意的i=1,…,n，当t→∞时，˜→0和→0成立，即证得定理1。注1：由式（23）可知，单调递减，为了避免过小使得控制器双曲正切函数接近符号函数产生系统抖振，可以选取较小的γd，使得较小，因此下降较慢。同时可以看出所设计的控制器是连续的，能够同时抑制扰动和模型参数不确定性。

注2：文献[9]利用滑模控制的思想给出了航天器编队鲁棒自适应姿态协同控制策略，然而，为了抑制扰动和模型参数不确定性，控制器含有符号函数，使得系统可能发生“抖振”现象。虽然文献[9]的注1提出了采用饱和函数或边界层法减弱抖振，但是在这种情况下一般无法得到系统渐近稳定的结论，最多只能得到系统是最终一致有界稳定的。而本文中提出了一种连续的鲁棒自适应姿态协同控制策略，由于控制器不含有符号函数，能够避免“抖振”现象。

3 数值仿真

为了验证控制器（20）～（23）的有效性，下面考虑4颗航天器编队的情况，并进行仿真验证。设4颗航天器的转动惯量矩阵分别为：

航天器的初始姿态和角速度分别为：

期望角速度和期望姿态的初始值设定为：

航天器受到的干扰力矩设为：

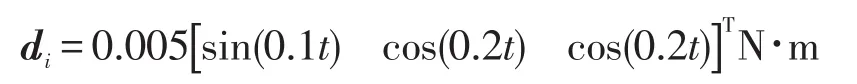
控制器（20）～（23）中参数选取为：

具体仿真结果如图1～图4所示。

编队航天器姿态跟踪误差如图1所示。从图1中可以看出，4颗编队航天器姿态跟踪误差均在10s左右收敛到零，能够较快跟踪到期望姿态，实现姿态的协同控制。图2给出了编队航天器的角速度跟踪误差，从图2中可以看出，航天器角速度跟踪误差也能够较快收敛到期望的角速度，说明所提出的控制其能够实现角速度的协同控制。

图1 姿态跟踪误差Fig.1 The errors of attitude tracking

图2 角速度跟踪误差Fig.2 The errors of angular velocity tracking

图3 自适应参数和Fig.3 The adaptive parametersand

4 结论

针对航天器编队飞行姿态协同控制问题，在有向通信拓扑的情况下提出了一种鲁棒自适应控制策略，能够克服外部干扰和内部参数不确定性的影响。和传统的滑模控制等非连续鲁棒控制不同的是，本文提出的控制器是连续的，更便于航天器编队系统的实现。同时数值仿真验证了文中给出的控制方法的有效性，各编队航天器稳态误差较小，能够满足航天器编队飞行控制精度要求。在提出的鲁棒自适应控制器中，任意编队航天器均需要获取期望信息，因此如何在仅有部分航天器获取期望信息的情况下，设计鲁棒自适应姿态协同控制策略，有待于进一步的研究。

[1]VanDyke M C,Hall C D.Decentralized coordinated attitude control within a formation of spacecraft[J].Journal of Guidance,Control,and Dynamics,2006,29(5): 1101-1109.

[2]Ren W.Distributed attitude alignment in spacecraft formation flying[J].International Journal of Adaptive Con-trol and Signal Processing,2007,21(2-3):95-113.

[3]Sarlette A,Sepulchre R,Lenoard N E.Autonomous rigid body attitude synchronization[J].Automatica,2009,45 (2):572-577.

[4]Dimarogonas D V,Tsiotras P,Kyriakopoulos K J.Leader-follower cooperative attitude control of multiple rigid bodies[J].Systems&Control Letters,2009,58(6):429-435.

[5]Ren W.Distributed cooperative attitude synchronization and tracking for multiple rigid bodies[C]//.IEEE Transactions on Control Systems Technology,2010,18(2): 383-392.

[6]Lawton J R,Beard R W,Hadaegh F Y.Elementary attitude formation maneuvers via leader-following and behavior-based Control[C]//.AIAA-2000-4442,2000.

[7]Lawton J R,Beard R W.Synchronized multiple space craft rotations[J].Automatica,2002,38(8):1359-1364.

[8]Wu B,Wang D.Decentralized robust adaptive control for attitude synchronization under directed communication topology[J].Journal of Guidance,Control,and Dynamics,2011,34(4):1276-1282.

[9]张海博,胡庆雷,马广富.基于有向图的航天器编队鲁棒自适应姿态协同跟踪控制[J].宇航学报，2012，33 (8)：1072-1079.

[10]Olfati-Saber R,Fax J A,Murray R M.Consensus and cooperation in networked multi-agent systems[C]//.Proceedings of the IEEE,2007,95(1):215-233.

[11]Wallsgrove R J,Akella M R.Globally stabilizing saturated attitude control in the presence of bounded unknown disturbances[J].Journal of Guidance,Control, and Dynamics,2005,28(5):957-963.

[12]Nuno E,Ortega R,Basanez L.Synchronization of networks of nonidentical Euler-Lagrange systems with uncertain parameters and communication delays[C]//. IEEE Transactions on Automatic Control,2011,56(4): 935-941.

[13]Khalil H K.Nonlinear systems[M].Upper Saddle River, New Jersey:Prentice-Hall,2002.

[14]Desoer C A,Vidyasagar M.Feedback system:input-output properties[M].New York:Academic Press,1975.

AdaptiveAttitude Cooperative Control for Spacecraft Formation Flying Under Directed Communication Topology

DANG Hong-tao1,2,YI Guo-xing1,LI Qing-hua1
(1.Space Control and Inertial Technology Research Center,Harbin Institute of Technology,Harbin 150001,China; 2.96117 Troops,Laiwu 271100,China)

The adaptive attitude cooperative control problem for formation spacecraft is studied under the directed communication topology.For the case of external disturbances and model uncertainty in the spacecraft formation flying system,an auxiliary variable including relative attitude errors and absolute attitude errors is selected and a robust adaptive control strategy is proposed.The adaptive laws are presented to estimate the unknown parameters of inertia matrices and the upper bound of external disturbances,and the asymptotic stability of closed-loop system is analyzed by using Lyapunov stability theory.Different from traditional robust control such as sliding mode control,the designed robust adaptive controller is continuous,which is convenient to realize spacecraft formation flying systems.Finally,the simulation results show that the control strategy can achieve high-precision tracking control of formation flying.

Formation flying；Directed graph；Cooperative control；Asymptotic stability；Adaptive law

V448.2

A

2095-8110（2015）02-0007-06

2014-07-03；

2014-10-10。

党宏涛（1976-），男，工程师，博士研究生，主要从事导航、制导与控制方面研究。E-mail:skydht@163.com