基于E-bayes的F2群体胚乳性状QTL上位性的分析

余 尘, 温永仙

(1.福建农林大学计算机与信息学院;2.福建农林大学生命科学学院，福建 福州 350002)



基于E-bayes的F2群体胚乳性状QTL上位性的分析

余 尘1,2, 温永仙1

(1.福建农林大学计算机与信息学院;2.福建农林大学生命科学学院，福建 福州 350002)

在F2群体中，采用经验贝叶斯统计方法(E-bayes)对谷类作物的胚乳性状QTL进行上位性分析，并通过计算机模拟加以验证.研究表明，基于E-bayes的胚乳性状QTL上位性分析，能准确地定位各QTL，同时有效地估计出QTL的各种遗传效应.

胚乳性状; 上位性; 经验贝叶斯(E-bayes); QTL

自上个世纪以来，谷类作物品质性状的遗传改良渐渐成为国际上的一大育种目标.胚乳作为谷类作物种子的重要部分，其数量性状表现往往决定了该谷类作物的品质.因此如何对胚乳性状进行准确而有效的QTL定位对于谷物改良具有重要意义.胚乳是显花植物双受精的产物，属于三倍体组织，早期人们将二倍体QTL定位方法直接应用到胚乳性状QTL分析中[1-2].Wu et al[3-13]相继提出了一系列基于胚乳性状三倍体的数量遗传模型的胚乳性状QTL定位，通常是应用线性回归分析方法[4-11].Wang et al[14]率先提出胚乳性状QTL区间作图的贝叶斯方法，但该方法是基于单QTL模型的区间作图.Wang et al[15]又提出将胚乳性状单QTL模型扩展为多QTL模型的方法，并研究出基于MCMC算法[16]的贝叶斯方法和程序.虽然该方法能够准确地估计胚乳性状QTL的位置和效应，并可有效区分2种显性效应，但是运算量超负荷.而Xu[17]、Cai et al[18]提出应用经验贝叶斯(E-bayes)方法进行二倍体QTL定位分析，改进了贝叶斯方法运算超负荷的缺陷.

但是以上提到的三倍体QTL定位方法皆未考虑到上位性效应.上位性效应是进化的遗传基础和群体进化的动力.在经典数量遗传学中，程君奇等[19]曾提出在双列杂交体系的基础上建立一个遗传模型对三倍体胚乳性状以及上位性进行分析，并利用混合线性模型[20-21]对这个遗传模型进行分析，采用最小范数二阶无偏估算法[20-21]估算无偏性.He et al[22]基于随机交配设计和种子混和测定，应用惩罚最大似然法进行胚乳性状的QTL上位性定位分析.

本文提出利用经验贝叶斯方法进行胚乳性状QTL的上位性分析.标记信息来自种子胚，性状表型值信息来自同一粒种子的胚乳，在此基础上建立胚乳性状QTL定位的遗传模型.利用该模型研究胚乳性状的QTL上位性效应；应用经验贝叶斯方法进行参数估计和检验；最后利用计算机模拟该方法的有效性和可行性.

1 试验设计

将数量性状上具有显著差异的2个自交系亲本进行杂交(P1×P2)，得到F1，再利用F1自交产生F2群体.其中标记基因型信息通过从来自父本和母本F2的二倍体组织种子胚中提取DNA分析获得；而胚乳性状表型值则来自F2中的胚乳.

对于上述F2群体种子的胚乳，鉴于母体(F1)植株在发育过程中并没有出现遗传分离，因此假定F2种子胚乳性状不存在母体效应，胚乳性状QTL效应仅仅来自于胚乳基因组自身.

Mo[23]于1987年首先提出胚乳性状三倍体模型,认为对于1对等位基因Q和q,F2种子胚乳性状具有QQQ、QQq、Qqq和qqq 4种基因型，而不是通常的QQ、Qq、qq 3种基因型；1对等位基因Q和q有3种遗传效应，即等位基因Q替代的平均替代效应(加性效应a)、等位基因QQ和q的互作效应(第一显性效应d1)、等位基因Q和qq的互作效应(第二显性效应d2).F2种子胚乳性状相应的基因型效应分别为:μ1=μ+3a/2,μ2=μ+a/2+d1,μ3=μ-a/2+d2和μ4=μ-3a/2(μ表示群体均值).

2 遗传模型

2.1 具有上位性的数量遗传模型

本文基于高密度分子标记连锁图谱,通过假定每个标记为可能的QTL进行分析,根据文献[17]，上位性的遗传模型可写成：

(1)

其中y=(y1,……yn)T表示n个数量性状表型值，t=(t1,……,tn)T和δ表示一些已知影响y的某些系统环境变量和其他效应，例如时间和空间因素等，将其纳入模型以减少剩余误差方差.gl=(g1l,……,gnl)T是座位l的基因指示变量，其中gil(i=1,……,n;l=1,……,e)表示在座位l上第i个个体上的基因型指示变量.gl⊗gl′表示向量gl和gl′对应元素相乘，αl表示座位l上的主效应，αll′则表示座位l和l′间的上位性效应,同时ε～N(0,σ2I).

2.2 胚乳性状遗传模型

假设群体大小为n，q表示控制胚乳性状QTL数目，由于设定的群体胚乳性状表达不受母体效应的影响，并且充分考虑所有成对QTL之间的上位性，据式(1)，胚乳性状QTL的遗传模型为：

(2)

3 参数估计和统计检验

结合式(1)、式(2)，且考虑到模型中主效应与上位性效应的处理方法相同，将模型写成

(3)

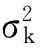
y=xβ+Zγ+ε

(4)

(5)

因此，y的协方差矩阵表示如下：

(6)

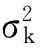
3.1 参数估计

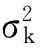
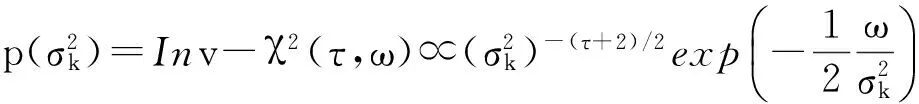
(7)

因此其数值迭代步骤表示如下：

(1)更新混合效应:

(8)

(2)更新剩余方差：

(9)

(3)更新G使得下式函数达到最大的Gi：

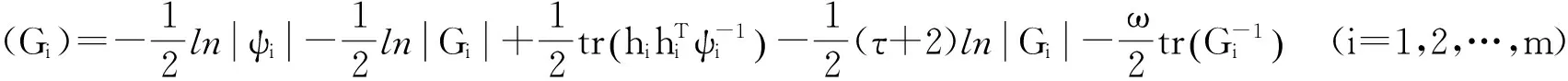
(10)

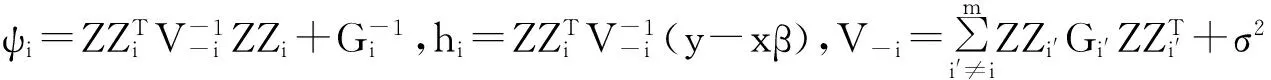
式(10)对Gi求偏导为零，得到

(11)

(12)

(4)重复步骤(1)-(3)直至最终收敛.

3.2 γj的Bayesian估计

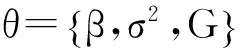
(13)

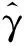
3.3 检验统计

提出2个步骤来甄别QTL.第1步：暂不考虑上位性，将每个标记分别假定为QTL进行逐个搜索.第2步：在第1步搜索出QTL的基础上，在遗传模型中考虑上位性效应，再重新应用E-bayes方法进行分析，具体步骤如下：

(1)检测QTL的存在性，假设H0∶LA=0和H1∶LA≠0，其中L=(1,0,0)、(0,1,0)和(0,0,1)，A=(a,d1,d2)T.

(2)检测QTL之间上位性效应的存在性，在第1步搜索到QTL的基础上，考虑到上位性效应.设H0∶LA=0和H1∶LA≠0，重新定义L矩阵：

L=diag(1,1,……,1)15×15

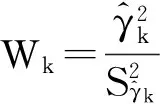
3.4QTL的遗传率

对于混合线性模型(式(2))，性状表型方差可以表述为：

(14)

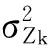
(15)

3.5 十折交叉验证

(16)

如此轮流试验10次，得到十折交叉验证标准误差为：

(17)

4 模拟分析

4.1 模拟设计

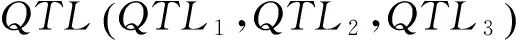
在模拟中，考虑以下几方面：(1)样本容量，种子数取2个水平(200，600)，暂不考虑极端大样本的情况；(2) QTL遗传力大小，假定群体环境方差分别为5和10,可得QTL总遗传率分别为67%和49%.当环境方差为5时，由于全部标记所贡献的遗传方差(包括主效应和上位性效应)大约是24.5，协方差为2.5，因此总表型方差为37.0.各遗传率大小见表1.100次参数估计的标准误偏差提供了参数估计误差标准，每个效应的显著性阈值均在显著性水平为0.05下进行检验，即自由度为1的卡方分布(3.84).统计功效为100次模拟中似然比测验统计量大于阈值的总数.

逆卡方先验中关于(τ,ω)这2个超参数的选取，通过式(17)计算选定.考虑到方法的收敛性以及统计功效等各方面的因素，选定以下几个组合进行验证,从中选取1个最优值，结果见表2.

表1 QTL的位置和效应的真值和遗传率

表2 十折交叉验证模拟结果

在逆卡方先验方法中，择定(τ,ω)=(5,1.5),全部模拟结果见表2.

4.2 模拟结果

由表3可知，基于E-bayes进行胚乳性状QTL上位性的定位分析能够得到较好的模拟结果.在绝大多数情况下逆卡方先验方法都能较为准确地检测到QTL位置和估计各种遗传效应(表3).

表3 各处理下QTL的位置和效应的估计值和标准误

在所有的模拟中，检测的QTL统计功效几乎均达到了100%.QTL效应值(a,d1,d2)和位置估计值均具有较高的准确度和精确度.从结果上看，即便是在样本容量较小而环境方差较大时，不仅主效应能够被检测出来，加加上位性的效应值也能够被检测出来，且也具有较高的统计功效.

在样本容量为200、600以及群体环境方差分别为10和5的情况下，QTL位置估计值相当准确，差异很小.而QTL效应估计值则随着样本容量的逐步增多以及遗传率的逐步增大，模拟的QTL的加性效应、第一显性效应、第二显性效应以及QTL之间的加加上位性互作效应，功效逐步提升，标准误不断减小，效应估计值精度越来越高.

即使在小样本(200粒F2种子)情况下，仍能够准确地估计出QTL的位置以及加性效应和加加上位性，虽然显性效应(包括d1和d2)的统计功效并不是太理想，只有80%左右，但只要提高样本容量，在样本容量较大(600粒F2种子)的情况下，显性效应(包括d1和d2)的统计功效大大提高，达到98%以上.在试验设计中，当样本容量较大(600粒F2种子)时，有的标准误已经达到0.01.

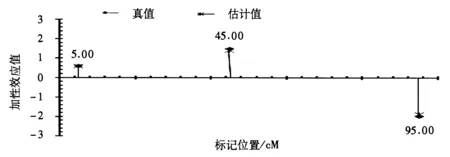
图1 染色体水平QTL加性效应真值与估计值位置分布图

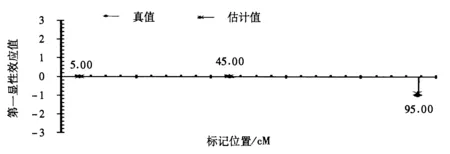
图2 染色体水平QTL第一显性效应真值与估计值位置分布图

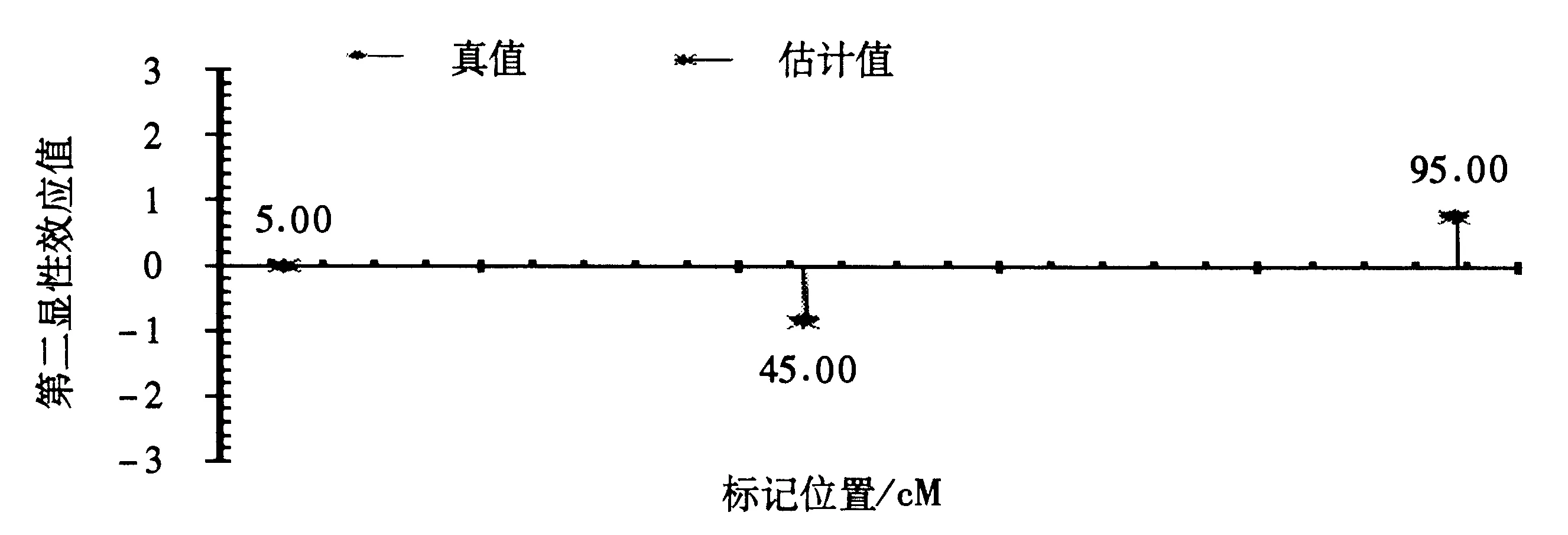
图3 染色体水平QTL第二显性效应真值与估计值位置分布图

5 讨论

本文应用E-bayes方法进行胚乳性状QTL主效应以及上位性的定位分析，准确性、精确度高，统计功效较好.从理论上来说，全贝叶斯方法的计算负荷大，且太依赖于方差部分的先验选择[17]，而本文提出的E-bayes方法能够克服这些缺点.同时本文所采用的E-bayes方法引入了分块坐标下降法，能够解决传统方法中只有在维数较小的情况下功效才能较好以及高维数模型下计算量大的问题.将分块下降法替代原有的逐个计算方法[25]，在时间效率上有明显的提高[25].因此E-bayes能有效地减少计算机的计算量，能够处理大规模数量的可能效应值，包括显性、加性、上位性、环境效应，还有基因与环境间的互作效应等.

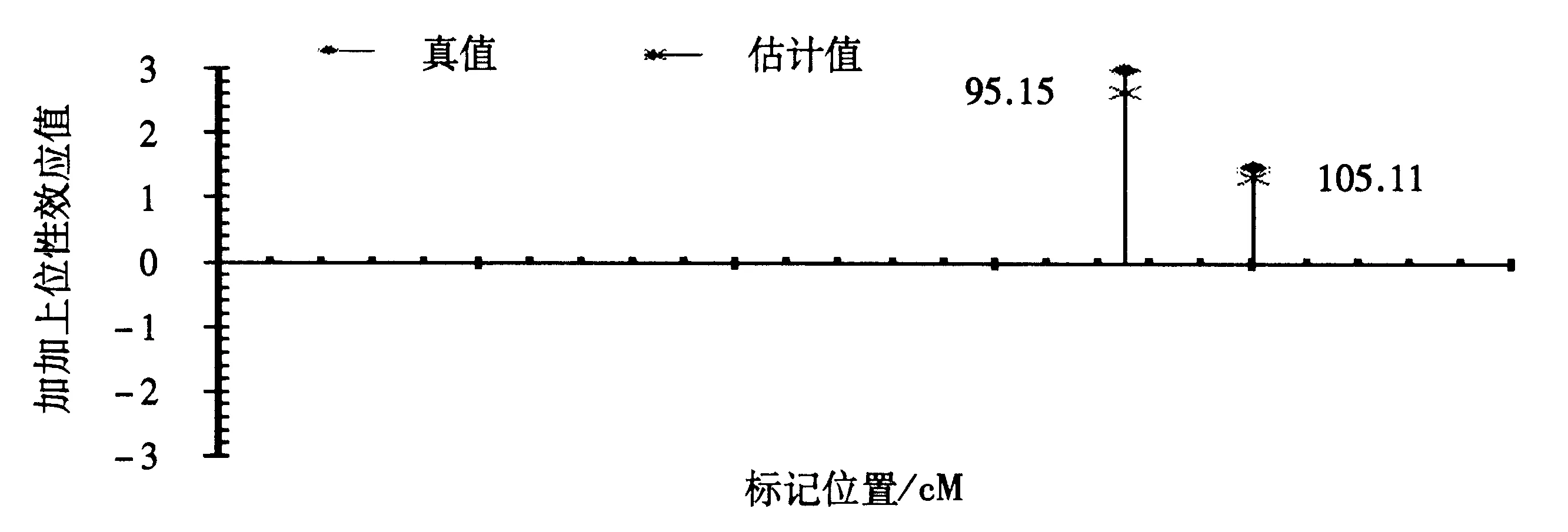
图4 染色体水平QTL上位性效应真值与估计值位置分布图

由于本文应用E-bayes进行统计分析是假定每个标记为可能的QTL,所以该法适用于高密度分子标记连锁图谱分析.

[1]WANGXL,LARKINSBA.Geneticanalysisofaminoacidaccumulationinopaque-2maizeendosperm[J].PlantPhysiol, 2001,125:1766-1777.

[2] WANG X L, WOO Y M, KIM C S, et al. Quantitative trait locus mapping of loci influencing elongation factor lacontent in maize endosperm[J]. Plant Physiol, 2001,125:1271-1282.

[3] WU R L, LOU X Y, MA C X, et al. An improved genetic model generates high resolution mapping of QTL for protein quality in maize endosperm[J]. PNAS, 2002,99(17):11281-11286.

[4] XU C, HE X, XU S Z.Mapping quantitative trait loci underlying triploid endosperm traits[J]. Heredity, 2003,90(3):228-235.

[5] WU R L, MA C X, MARIA G M, et al. Statistical methods for dissecting triploid endospermtraits using molecular markers: an autogamous model[J]. Genetics, 2002,162:875-892.

[6] WEN Y X, WU W R. Methods for mapping QTLs underlying endosperm traits based on random hybridization design[J]. Chinese Science Bulletin, 2006,51(16):1976-1981.

[7] KAO C H. Multiple-interval mapping for quantitative trait loci controlling endospermtrait[J]. Genetics, 2004,167(4):1987-2002.

[8] CUI Y, WU R L. Statistical model for characterizing epistatic control of triploid endosperm triggered by maternal and offspring QTLs[J]. Genetical Research, 2005,86:65-75.

[9] HU Z Q, XU C W. A new statistical method for mapping QTLs underlying endospermtraits[J]. Chinese Science Bulletin, 2005,50(14):1470-1476.

[10] WEN Y X, WU W R. Interval mapping of quantitative trait loci underlying triploid endospermtraits using F3 seeds[J]. Journal of Genetics and Genomics, 2007,34(5):429-436.

[11] WEN Y X, WU W R. Experimental designs and statistical methods for mapping quantitative trait loci underlying triploid endosperm traits without maternal genetic variation[J]. Journal of Heredity, 2008,99(5):546-551.

[12] 何小红.应用遗传交配设计检测数量性状上位性QTL方法的研究[D].南京:南京农业大学,2010.

[13] 温永仙.基于BC1F1:2种子的胚乳QTL区间定位[J].生物数学学报,2011,3:540-546.

[14] 王亚民,孙长森,汤在祥，等.谷物胚乳性状QTL区间作图的贝叶斯方法[J]．扬州大学学报：农业与生命科学版,2008,29(3):12-17.

[15] 王亚民,汤在祥,陆鑫,等.基于贝叶斯统计的谷物胚乳性状QTL多区间作图方法[J].作物学报,2009,35(9):1569-1575.

[16] XU S Z, HU Z. Mapping quantitative trait loci using the MCMC procedure in SAS[J]. Heredity, 2010,106(2):357-369.

[17] XU S Z. An empirical Bayes method for estimating epistatic effects of quantitative trait loci[J]. Biometrics， 2007,6(63):513-521.

[18] CAI X D, HUANG A H, XU S Z. Fast empirical Bayesian LASSO for multiple quantitative trait locus mapping[J]. BMC Bioinformatics, 2011,12:211-224.

[19] CHEN J Q, WU J G, SHI C H, et al. Analysis of epistasis: a genetic model for triploid endosperm traits[J].Journal of Zhejiang University，2007,33(1):1-7.

[20] ZHOU X, MATTHEW S. Genome-wide efficient mixed-model analysis for association studies[J]. Nature Genetics, 2012,7(44):821-824.

[21] 梁文科,张世煌,戚廷香,等.应用混合线性模型(AD)分析热带温带玉米群体间的遗传关系[J].作物学报,2006,32(7):1018-1023.

[22] HE X H, ZHANG Y M. Mapping epistatic quantitative trait loci underlying endosperm traits using all markers on the entiregenome in a random hybridization design[J]. Heredity, 2008,101:39-47.

[23] Mo H D, Genetic Expression for Endosperm Traits[R]. Raleigh: North Carolina State University, 1987.

[24] SYLVAIN A. A survey of cross-validation procedures for model selection[J]. Statistics Surveys, 2010,4:40-79.

[25] XU S Z. Principles of Statistical Genomics[M]. NewYork:Springer, 2012:259-266.

(责任编辑:叶济蓉)

Epistatic anlysis of the quantitative trait loci underlying triploid endosperm traits in F2populations based on Empirical bayes

YU Chen1,2, WEN Yong-xian1

(1.College of Computer and Information Science; 2.College of Life Science, Fujian Agriculture and Forestry University, Fuzhou, Fujian 350002, China)

In F2populations, Empirical bayes (E-bayes) method was used to analyze the epistasis of quantitative trait loci (QTL) underlying endosperm traits. The feasibility and efficiency of the method were verified by Monte Carlo simulations. The result showed that the method could efficiently detect endosperm QTLs and precisely estimate their epistatic effects.

endosperm trait; epistasis; Empirical bayes(E-bayes); quantitative trait loci (QTL)

2014-09-23

2015-01-22

国家自然科学基金资助项目(31171448);福建省自然科学基金资助项目(2012J01069).

余尘(1990-),女,硕士研究生.研究方向:生物信息学.通讯作者温永仙(1966-),教授,博士生导师.研究方向:生物信息学.Email:wen9681@sina.com.

S330

A

1671-5470(2015)04-0337-08

10.13323/j.cnki.j.fafu(nat.sci.).2015.04.001