一种改进的人工鱼群算法
崔丽英,黄殿平,宋晓阜新市第一中等职业技术专业学校;辽宁工程技术大学
一种改进的人工鱼群算法
崔丽英1,黄殿平2,宋晓2
1阜新市第一中等职业技术专业学校;2辽宁工程技术大学
摘要:人工鱼群算法是一种高效的群体智能寻优算法。本文提出一种改进智能鱼群算法,引入云学习因子和云变异因子,使算法在寻优过程中的学习能力有所提高,避免算法在寻优过程中游动行为的不确定性,提高了算法的寻优能力。
关键词:鱼群算法;云模型;优化
1 引言
2002年,我国知名学者李晓磊[1-2]提出了人工鱼群算法(Artifi⁃cial Fish-swarm Algorithm,AFSA)理论,AFSA主要是通过仿生鱼的觅食、群聚、游弋和追尾行为,从单条人工鱼的底层局部寻优从而达到群体全局寻优。由于AFSA鲁棒性强,算法简单且容易实现,一经提出就引起了广泛关注[3]。本文为了解决鱼群进化过程中随机性与倾向性的兼容问题,采用云模型的思想,提出一种基于云的人工鱼群算法(Cloudy Model-Artificial Fish-swarm Algorithm,CMAFSA)。
2 AFSA和CM-AFSA
2.1AFSA算法
在AFSA算法中,N表示鱼群容量,Visual代表可视域,Step代表步长,Try_number代表迭代次数,δ为拥挤度因子,每个人工鱼的状态表示为X=(x1,x2,…,xn),其中xi(i=1,2,…,n)代表寻优变量。Y=f(X )代表人工鱼食物浓度,其中Y为目标函数值,表示两个人工鱼个体之间的距离。
2.1.1追尾行为
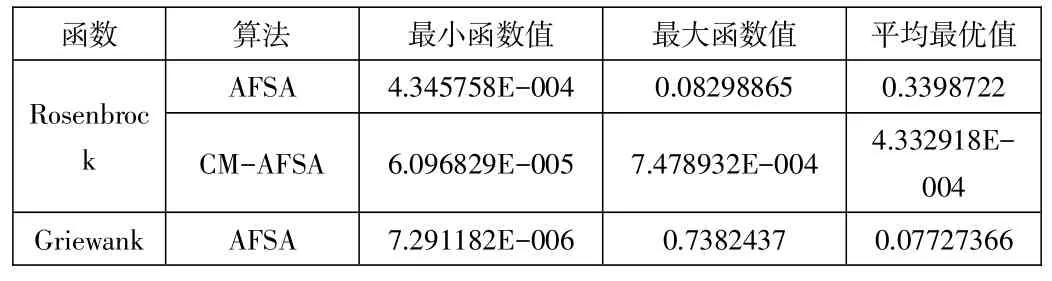
设Xi为人工鱼此刻的位置状态,在可视域范围内搜索此刻最优的人工鱼Xmax,当Yi 2.1.2觅食行为 设Xi为人工鱼此刻的位置状态,该人工鱼在其可视域内搜索,若发现有状态Xj,且Xj所在位置的食物浓度Yj大于当前状态Xi的食物浓度,那么当前人工鱼将会朝该方向移动一步;否则,如果Xj所在位置的食物浓度小于当前食物浓度,那么在可视域内随机选择下一个状态再次与当前状态进行比较。尝试Try_number次后,如果在该可视域中无更优状态,那么此人工鱼随意移动一个步长。 2.1.3群聚行为 设Xi为人工鱼此刻的位置状态,其可视域内所有人工鱼的集合为S。 如果存在非空集合S,则表示此刻人工鱼可视域内存在其他人工鱼,其鱼群容量Nf≥1,如果当前状态Yi 2.1.4随机行为 人工鱼的随机行为是人工鱼觅食行为的缺省行为之一,在此刻人工鱼可视域范围内随意选定其后一状态并向此状态前进一个步长。此行为为人工鱼个体提供随机游弋的机会,可以提高种群多样性,同时能够跳出局部最优以达到全局最优。 3.1云模型定义 云模型是李德毅院士提出的一种定性定量转换模型[4],可以实现定性与定量间的不确定性转换。设U是一个普通集合表示的论域,C对应论域U上相联系的语言值,存在数值x∈U,满足x~N(Ex,)是C的一次随机实现,其中En1~N(En,),数值x对C的确定度μ(x)∈[0,1]是具有稳定倾向的随机数。若 则x在论域U上的分布称为云模型,简称云[5]。 3.2云模型的数字特征 云用期望Ex(Expected value)、熵En(Entropy)和超熵He(Hy⁃per entropy)三个数字特征来整体表征一个概念,多个数字特征的组合能够体现云模型在全局中的特性[3]。 3.3云发生器 按云的产生机理和计算方向,有正向云和逆向云[6]。它是整个云模型的核心理论。 3.3.1正向云 正向云是依据云模型的数字特征将定性概念转化为定量数值,其方法是通过云的数字特征(Ex,En,He)来生成云滴,此过程是直接前向的,如图1所示。输入定性概念的Ex、En以及He,根据对应关系输出云滴drop(xi,μi),其中xi代表定性概念在U中的位置,μi是隶属度。 图1 正向云发生器 3.3.2逆向云 逆向云实现定量值与定性概念之间过程转换,该发生器能把数据转换成具有数字特征(Ex,En,He)来进行表达。如图2所示,逆向云是于统计原理思想设计的。 图2 逆向云发生器 针对AFSA后期收敛性差、易陷入局部最优等缺点,本文将云的概念引入到鱼群算法中进行建模,通过正太云实现人工鱼的自适应进化,引入云变异的均衡概念,提出了一种基于云模型的人工鱼群算法。CM-AFSA与其他AFSA改进算法的区别在于增加了鱼群的自主学习能力,对云参数进行了自适应处理。CM-AFSA引入云学习因子和云变异因子。 云学习因子是在鱼群学习过程中,两个适应度不相同的个体人工鱼,通过正态云产生新人工鱼的过程。设xf、xm为互相进化的两个人工鱼的当前状态,Ff、Fm为两个人工鱼个体适应度,则云学习因子的期望、熵、超熵为: 云变异因子是在鱼群在学习过程中,人工鱼通过自身携带的适应度,再通过正态云产生新人工鱼的过程。设xi是当前某个人工鱼状态,Fi是此个个体的适应度,则云变异因子的期望、熵、超熵分别为: CM-AFSA算法描述如下: (1)由适应度函数定义,在U中随机产生n个人工鱼x1,x2,…,xn,初始化种群X={x1,x2,…} ,xn,步长Step、可视域Visual、拥挤度δ和代数Try_number; (2)计算每个人工鱼适应度f(x),结果按升序排序,记录最优人工鱼、最大、最小适应度xbest、Fmax、Fmin; (3)计数器i=1; (4)对第i条鱼进行追尾行为,判断当前可视范围内最大人工鱼的邻域是否拥挤,若不拥挤执行追尾行为,否则执行(5); (5)对于人工鱼xi,当i≤0.618n时,启动云变异因子,对符合条件的人工鱼个体进行操作;否则启动云学习因子,对符合条件的人工鱼个体进行操作; (6)比较(4)和(5)得到的结果,更新公告板; (7)判断是否处理完所有人工鱼,若满足,则执行(8),否则执行(4); (8)若满足终止条件,算法优化结束;否则执行(3)。 为验证算法的性能,实验选用了4个经典的测试函数。因为这4个函数都存在多极值点、震荡性的特性,因此国内外学者用这几个函数做实验对象。本次实验环境为Windows7系统、Intel CoreI3处理器,编译工具采用Matlab7.0,测试函数如下: (1)Rosenbrock函数 5.1固定收敛精度 实验参数为:鱼群规模为50,代数为500,收敛精度为0.01%,步长Step=0.7,可视域Visual=3,最大迭代次数Try_number=50,拥挤度δ=8。对4个函数分别独立进行100次运行,实验结果见表1和表2。 对比表1和表2可以得出,对于多极值点、震荡性的函数寻优测试结果,相对于AFSA算法,CM-AFSA算法的平均代数和所用时间有了显著的降低,尤其是使用Rastrigin函数进行测试时,改进鱼群算法的平均代数从326次下降到181次,迭代时长也由24.075s下降到9.614s,进一步证明了CM-AFSA算法具有较强的寻优能力。 表1 固定收敛精度时AFSA算法优化代数 表2 固定收敛精度时CM-AFSA算法优化代数 5.2固定代数 实验参数为:鱼群规模50,Try_number=50,δ=8,代数为100,由于各函数的复杂度不同,对每个测试函数参数见表3,对函数分别采用基本AFSA和CM-AFSA独立运行50次,实验数据见表4,收敛曲线如图3~图6所示。 表3 实验参数设置 表4 相同代数下函数求解最优值表 Rastrigin Dejong's f6 CM-AFSA AFSA CM-AFSA AFSA CM-AFSA 1.239403E-008 4.387534E-004 5.723462E-008 6.325362E-011 0 0.00375632 0.389327 3.374859E-006 0.427223 2.836542E-010 4.298762E-004 0.0974563 1.230092E-007 5.342881E-003 9.372537E-12 从表4可以看出,在代数一定的情况下,改进后的鱼群算法50次优化均值和50次优化结果的最优值明显的优于基本鱼群算法算法,相对于基本鱼群算法,改进后的鱼群算法具有较强的全局搜索能力,结果更稳定,鲁棒性更强。 图3 Rosenbrock函数优化曲线 图4 Griewank函数优化曲线 图5 Rastrigin函数优化曲线 图6 Dejong’sf6函数优化曲线 在图3~图6中,虚线代表基本鱼群算法的优化曲线,实线代表改进后的鱼群算法的优化曲线,横坐标为代数,纵坐标为函数适应值的对数。对比图3~图6可得,CM-AFSA算法能较快的收敛于全局最优,收敛性更优,如图3所示,基本鱼群算法在收敛后期陷入了局部最优值0.0019,而改进后的鱼群算法成功收敛到全局最优2.78×10-10。实验结果表明,CM-AFSA算法的明显提高了函数优化的收敛精度。 结束语:CM-AFSA通过引入云学习因子和云变异因子的概念,增强了鱼群算法的全局搜索能力,使鱼群算法的寻优精度更加精确,也有效的避免了基本鱼群算法容易陷入局部最优。将CMAFSA算法应用到复杂函数的寻优中,通过仿真测试可明显看出,基于云模型的人工鱼群算法相对于AFSA算法的性能在各方面都有显著的改善,尤其在跳出局部极值方面有表现优秀,但在处理高维函数时,由于云的引入使鱼群算法的算法复杂度更强,如何降低算法的复杂度提高效率需要进一步研究。 参考文献: [1]李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38. [2]李晓磊,钱积新.基于分解协调的人工蚁群优化算法研究[J].电路与系统学报,2003,8(1):1-6. [3]宋晓.基于云模型人工算法的应用研究[D].辽宁工程技术大学,2015. [4]李德毅,刘常昱.论正太云模型的普适性[J].中国工程科学,2004,6(8):28-34. [5]Li D,Liu C,Gan W.A new cognitive model:cloud model[J].International Journal of Intelligent Systems,2009,24(3):357-375. [6]段海滨,王道波,于秀芬等.基于云模型理论的蚁群算法改进研究[J].哈尔滨工业大学学报,2005,1(37):115-119. 崔丽英(1974-),女,硕士研究生,主要研究方向为计算机网络技术; 黄殿平(1989-),男,硕士研究生,主要研究方向为图形图像处理; 宋晓(1987-),女,硕士研究生,主要研究方向为图形图像处理。 作者简介:3 云模型
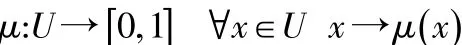


4 基于云模型的鱼群算法


5 仿真实验与性能测试