Improving the BER performance of turbo codes with short frame size based on union bound①

Shao Xia (邵 霞), Li Ping, Zhang Weidang

(*Department of Information Engineering, North China University of Water Resources and Electric Power, Zhengzhou 450011, P.R.China)(**Department of Information Management, Shengda Trade Economics & Management College of Zhengzhou, 451191, P.R.China)(***School of Information Engineering, Zhengzhou University, Zhengzhou 450001, P.R.China)



Improving the BER performance of turbo codes with short frame size based on union bound①

Shao Xia (邵 霞)*, Li Ping**, Zhang Weidang②

(*Department of Information Engineering, North China University of Water Resources and Electric Power, Zhengzhou 450011, P.R.China)(**Department of Information Management, Shengda Trade Economics & Management College of Zhengzhou, 451191, P.R.China)(***School of Information Engineering, Zhengzhou University, Zhengzhou 450001, P.R.China)

In order to improve the bit error rate (BER) performance of turbo codes with short frame size at a wide range of signal to noise ratio (SNR), a new method by optimizing the bit energy is proposed. At first, a formula derived from the Union Bound is introduced. It describes the relations between the bit error rate distribution and the minimum weight distribution. And then, by mathematically optimizing the formula, the energy for every bit of the codeword is optimized to achieve the minimum BER at high SNR region. At last, an adjustable parameter is employed to compensate the degradations of BER at low and moderate SNR regions. Case studies indicate that the improvements of BER for turbo codes with short frame size are significant at a wide range of SNR.

channel coding, bit error rate (BER), energy allocation, turbo code

0 Introduction

How to improve the bit error rate (BER) performance of turbo codes[1]is the most important task. There are many methods toward this destination. One of them is to reallocate the energy of the bit in the bit stream of the codeword. These schemes have previously been proposed in Refs[2-8]. In Ref.[2], the author assigned less and less power to the parity bits as the noise level increased to avoid the traditional negative “coding gain” associated with all error correcting codes at high noise levels. Ref.[3] showed that the fraction of the total power that should be allocated to a systematic bit was usually lower than that of the parity bit. But the amount of improvement depends on the choice of component codes, interleaver length and signal to noise ratio. Ref.[4] also pointed out that if different energies were assigned to two outputs of a turbo encoder, the information bit and parity bit, then the performance would be changed according to the ratio of the information bit energy to the parity bit energy. The optimum point of the ratio may not be 1. As the rate of the turbo code is changed, the optimum point would also be changed. In Ref.[5], it concluded that for turbo codes with short frames operating in very low signal-to-noise environments, more energy should be assigned to the systematic bits so that the performance was improved. At higher signal-to-noise ratios, allocating less energy to the systematic bits improved the performance. Ref.[6] studied the effect of asymmetric energy allocations to the output bits of turbo codes. It showed that the error floor was improved as more energy was given to the non-systematic bits. However, due to the degradation in the convergence threshold of the code, tradeoff between the error floor and the convergence threshold appeared. Ref.[7] studied theoretically and empirically channels coding for nonuniform i.i.d. sequences using turbo codes with unequal energy allocation. It was shown that both systematic codes and non-systematic codes with unequal energy allocation were improved on equal energy allocation schemes. Ref.[8] introduced a method of reducing the error floor in parallel concatenated codes. It also pointed out that simple approaches based on modifying just the energy of the systematic and coded bits seemed very attractive. From the references listed above we can see that nearly all of them allocate the energies between the systematic bits and parity bits, but the merits of different strategies are sometimes not very clear, with different authors arriving to contradicting conclusions[6]. This is because that there is no theoretical base for the energy allocation between the information bits and parity check bits. The fraction of the total energy depends on the choice of the component codes, interleaver length, puncturing pattern and the signal to noise ratio.

In Ref.[9], the authors allocated the bits’ energies among the codewords that have different weights instead of between the systematic and parity bits. In this scheme more energy is assigned to the codewords that have minimum (and second minimum) weight and the simulation results showed that the “error floor” of turbo codes was improved with no practical degradation in the waterfall region.

In this work, a new method is presented to decrease the bit error rate (BER) by optimizing the bit energy. It is based on a formula, which describes the relationships between the bit error rate distribution and the minimum weight distribution, derived from the union bound. Through mathematical optimization, the energy for every bit of the codeword is optimized to achieve the minimum BER at high SNR. Then by adding an adjustable parameter, the BER performance at low and moderate SNR regions is also improved.

The paper is organized as follows. A formula to estimate the BER distributions based on the union bound is introduced in Section 1. In Section 2, we firstly derive a formula to optimize the bit energy based on the BER distribution. Then we introduce an adjustable parameter to modify the energy distribution so that it can be used at low and moderate SNR regions. In Section 3, more detailed optimizing procedures are provided and various types of turbo codes are simulated to show the efficiency of the scheme. Section 5 is the conclusion.

1 Union bound and the formulas of the BER distribution

Let c=(c0, c1,…,cN-1) be a binary codeword, where N is the code length, cj=0 or 1 is called the j-th bit of the codeword. If a codeword is with ci=1, it is said that the i-th bit connects to this codeword, or this codeword connects to the i-th bit.

For an Additive White Gaussian Noise (AWGN) channel, the BER is bounded by the union bound as[10]

(1)

where wiand diare the information weight and total Hamming weight, respectively, of the i-th codeword. k is the input length. Rcis the code rate. Ebis the bit energy of the codeword and N0is the noise power spectrum density.

From Eq.(1), a formula to estimate the bit error rate for every position at higher SNR can be derived as[11,12]

(2)

where dmin(j) is the lowest weight of the codeword(s) that connects to the j-th bit and nmin(j) is its multiplicity, where j=0,1,…,N-1. We call the sequence (dmin(j), nmin(j), j=0,1,…,N-1) the distribution of minimum weight codewords.

Eq.(2) shows that, generally, bit error rates pb(j) are not identical for different j. For example, if a bit in the codeword sequence connects to a lower weight codeword, it will have a weaker error protection so the bit error rate for this bit will be higher. The average bit error rate of the code is dominated by such bits that connect to the low weight codewords. Therefore, if the bits’ energy is changed so that more energy is allocated to the bits that connect to low weight codewords and less energy to the bits that connect to high weight codewords, the average bit error rate will be decreased.

2 Optimizing the bit energy with an adjustable parameter

In Eq.(2), constant bit energy Ebby Eb(j) is replaced that is the optimized bit energy for the j-th bit and pb(j) is replaced by pob(j) that is the new bit error rate for bit j relating to Eb(j), then Eq.(2) becomes

(3)

(4)

Now the minimum value of average BER expressed by Eq.(4) will be found with the binding condition of energy conservation:

(5)

Using the Lagrange multiplier method, let λ be the multiplier, the formula of calculating the optimized bit energy Eb(j) can be derived and the result is

(6)

where

(7)

So Eb(j) expressed by Eq.(6) is the optimized energy for bit j. It is determined by the minimum weight distribution (dmin(j), nmin(j), j=0,1,2,…,N-1). Apparently, if dmin(j), as well as nmin(j), are constant, then Eb(j)=Eb. In this case, there is no need to modify the bit energy, such as the equal-weight codes that have perfect construction. But there are many codes, especially such as turbo codes, that don’t have such perfect construction. Their dmin(j)s usually expend to a wide range. In this case, there are much more spaces for the bit energy to be optimized and noticeable improvements can be achieved.

To calculate optimized bit energy Eb(j), the minimum weight distribution (dmin(j), nmin(j), j=0,1,2,…,N-1) should be found. If the code length is not long, for example, it is no longer than thousands bits, the methods presented in Refs[13-15] and [16] are very efficient to calculate the minimum distance of turbo codes. Through modifications, they can be used to find the parameters of dmin(j) and nmin(j).

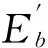
(8)

where ρ is the adjustable parameter.

Without loss of generality, assuming Eb=1, Eq.(9) can be got:

(9)

(10)

3 Optimization procedures and simulation results

The followings give the optimization procedures and simulation results. There are four turbo codes used in this section. The generator matrix for the four codes is the same, which is g=(1, 10001/10011). But they have different code lengths, different interleavers and different puncturing patterns. Code 1 is a turbo code with a 8×8 block interleaver of size 64 and without puncturing. So the code rate is 1/3. Another turbo code, noted as code 2, is with a 32×32 block interleaver. The puncturing pattern for this code is p=(10; 01). So the code rate is 1/2. There are other two turbo codes. Both of them use random interleavers, but the sizes are 64 and 1024 separately. The turbo code of size 64, noted as code 3, is not punctured. The turbo code of size 1024, noted as code 4, is punctured with puncturing pattern p = (10; 01). For all the turbo codes, the decoding algorithm is BCJR, the number of iteration is 5 and the two encoder components are both terminated. Binary antipodal signalling is used with an AWGN channel model. The SNR is measured in terms of energy per information bit, Eb, over the single-sided noise power spectral density, N0.

Based on code 3, which has the code length of N=(64+4)×3=204, the practical procedures of optimization will be given and used to show the efficiency of the proposed scheme.

Firstly, the minimum weight distribution (dmin(j), nmin(j) is searched, j=0,1,2,…,N-1) of the code by the method presented in Ref.[10] is searched. Fig.1 shows the distribution of the minimum weight (dmin(j), nmin(j), j=0,1,2,…,N-1) of code 3.

Fig.1 The minimum weight distribution (dmin(j), nmin(j), j=0, 1, 2, …,N-1) of code 3 calculated by the method presented in Ref.[10]

Secondly, the optimized bit energy distribution can be got by Eq.(6) with the minimum weight distribution (dmin(j), nmin(j), j=0,1,2,…,N-1). Fig.2 shows the bit energy distributions before and after energy optimization. Before energy optimization, the bit energy is the same for all bits in the codewords. The bit energy is assumed Eb=1. So curve 1 is a straight line with amplitude 1. After energy optimization, the distribution of bit energy is not even. Compared with Fig.1, apparently, more energy is allocated to the bits that connect to the lowest weight codeword and less energy is allocated to the bits connecting to high weight codewords.

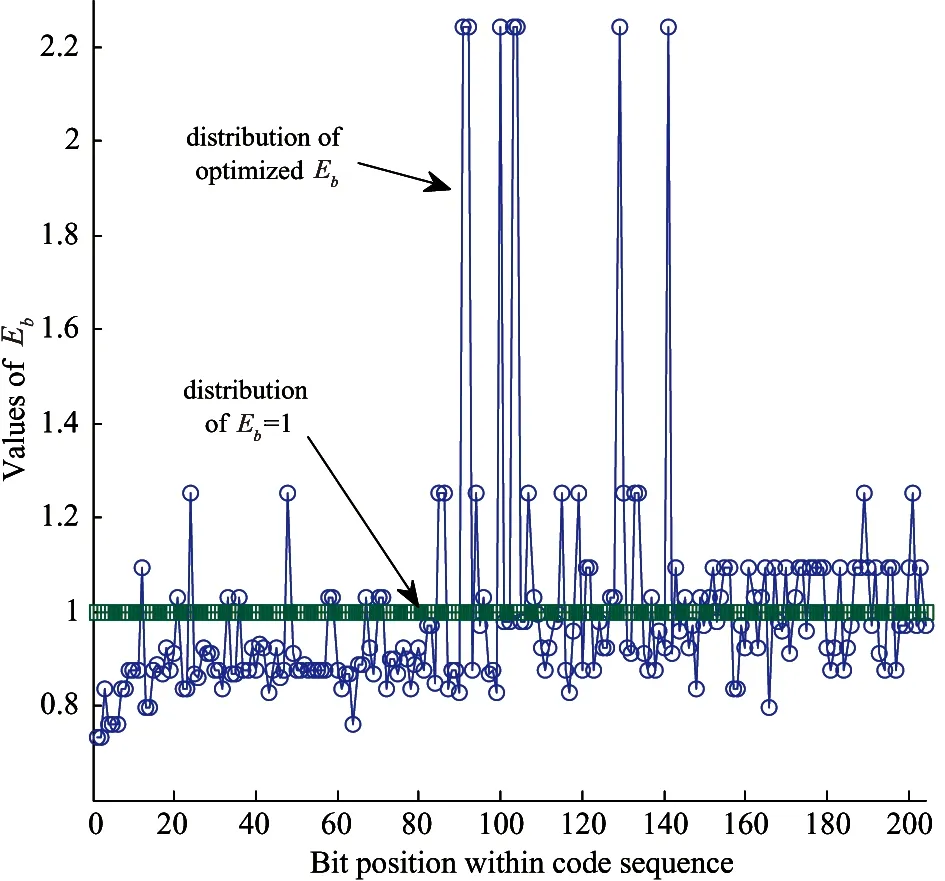
Fig.2 The bit energy distributions before and after energy optimization for code 3

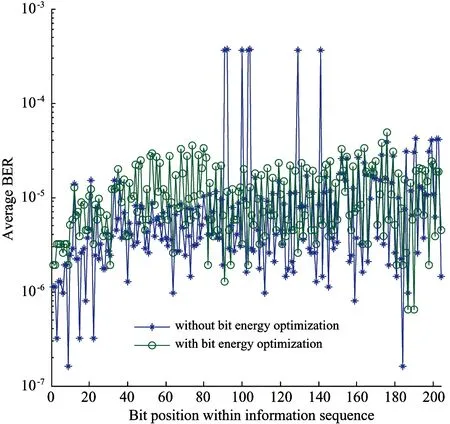
Fig.3 The BER distributions before and after energy optimization for code 3 at SNR=4dB

Table 1 shows the values of BER at different SNRs without and with bit energy optimization separately. By examining Table 1 we find that at high SNR region, such as 4dB and 5dB, the average BERs are improved obviously. But at low and moderate SNR regions, there even some degradations appeared.

Table 1 The average BER without and with energy optimization for code 3 at different SNRs

Finally, by modifying the optimized bit energy with adjustable ρ expressed by Eq.(8), the lowest BER at a wide range of SNR is got.

Table 2 shows the valid ranges of ρ constrained by Eq.(10) at some specific SNRs. The best values of ρ that produce the lowest BER at specific SNRs and the corresponding BERs are also displayed in the table. The best values of ρ are obtained by grid search within the valid ranges, starting from step size of 2, down to the finest step size of 0.25. From the table we can see that after modification with ρ, the BER performance is improved not only at high SNR region, but also at low and moderate SNR regions.

Table 2 The valid ranges of ρ at different SNRs, the best values of ρ and the corresponding values of BER for code 3

The BER improvements in the two figures are obvious. From the figures it can be seen that after energy optimizing, the BER curves corresponding to Eq.(6) are lower than the curves before energy optimizing at

Fig.4 The simulation BER curves before and after optimizing for code 1 and code 2

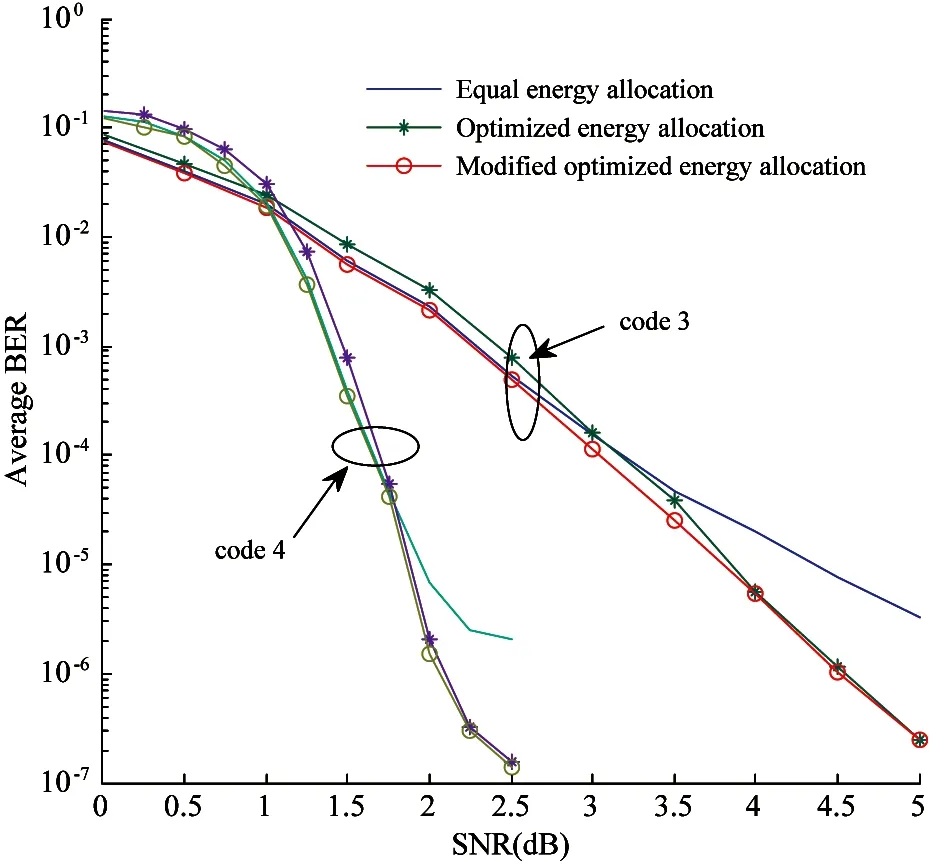
Fig.5 The simulation BER curves before and after optimizing for code 3 and code 4

high SNR regions. For example, the improvements are more than 1 order of magnitude at 4.5dB for turbo code 3 and at 2.5dB for turbo code 4. In the two figures that, with modification of Eq.(8), the BER performance at low and moderate SNR regions is improved and all the curves corresponding to Eq.(8) have the best performance.

So, by optimizing the bit energy distributions to the codeword sequences, the BER performance is improved noticeably. In fact, this scheme changes the weight of the codewords. For example, the minimum weight for code 3 is 7 before energy optimizing. After optimizing, this codeword’s weight is changed to 12 at 5dB. For code 2, the minimum weight is changed from 7 to 10 after optimizing at 4dB.

4 Conclusion

A new method to optimize the bit energy is presented in this work. By changing the bit energy allocation in an optimized way, the deviation of the BER distribution is decreased; the minimum weight of the codewords is increased; and the average BER is minimized over a wide range of SNR. However, this scheme is based on the minimum weight distribution (dmin(j), nmin(j), j=0,1,2,…,N-1). Finding the minimum weight distribution consume time very much especially when the code size is not short. Therefore the proposed scheme is suitable for turbo coded with short size. How to optimize the bit energy for the code with large size is further work.

[ 1] Berrou C, Glavieux A, Thitimajshima P. Near Shannon limit error-correcting coding and decoding: Turbo codes. In: Proceedings of the IEEE International Conference Communications, Geneva, Switzerland, 1993. 1064-1070

[ 2] Hokfelt J, Maseng T. Optimizing the energy of different bitstreams of turbo codes. In: Proceedings of the Turbo Coding Seminar, Lund, Sweden, 1998. 59-63

[ 3] Duman T M, Salehi M. On optimal power allocation for turbo codes. ISIT 1997, Ulm, Germany, June-July: 104

[ 4] Choi Y, Lee P. Analysis of turbo codes with asymmetric modulation, Electron. Lett., 1999, 35, (1): 35-36

[ 5] Salah M M, Raines R A, Temple M A, et al. Energy allocation strategies for Turbo codes with short frames. In: Proceedings of the International Conference on Information Technology: Coding and Computing (ITCC 2000), Las Vegas, USA, 2000. 27-29

[ 6] Cabarcas F, Garcia-Frias J. Asymmetric energy allocation strategies to improve Turbo codes performance. In: Proceedings of the Vehicular Technology Conference (VTC 2001 Fall). 2001, (3):1839-1842

[ 7] Shamir G I, Souza R D, Garcia-Frias J. Unequal energy allocation with Turbo Codes for nonuniform sources. In: Proceedings of the Turbo-Coding-2006, Munich, Germany, 2006. 1-6

[ 8] Garcia-Frias J, Cabarcas F. Reducing the error floor in turbo codes by using non-binary constituent encoders. In: Proceedings of the Vehicular Technology Conference, Boston, USA, 2000. 1230-1237

[ 9] Zhang W, Wang X. Optimal energy allocations for turbo codes based on distributions of low weight codewords, Electronics Letters, 2004,19(40): 1205-1206

[10] S. Benedetto, G. Montorsi, Unveiling turbo codes: Some results on parallel concatenated coding schemes, IEEE Trans. Inform. Theory, 1996,42(2): 1996. 409-428

[11] Shao X, Zhang W D. Estimate the BER Distributions of Turbo Codes, Wireless and Microwave Technologies, 2012, 2:53-58

[12] Zhang W D, Shao X, Torki M et al. Unequal error protection of JPEG2000 images using short block length turbo codes, Communications Letters, IEEE, 2011,15(6): 659-661

[13] Roberto G, Paola P, Sergio B. Computing the free distance of turbo codes and serially concatenated codes with interleavers: algorithms and applications, IEEE Journal on Selected Areas in Commun, 2001,19(5): 800-812

[14] Sandro S, Young-Jik K B, Harald E. A fast algorithm to estimate the distance spectrum of turbo codes. In: Proceedings of the 10th International Conference on Telecommunications (ICT 2003), Papeete, FR Polynesia, 2003. 90-95

[15] Crozier S, Guinand P, Hunt A. Estimating the minimum distance of turbo codes using double and triple impulse methods, IEEE Communications Letters, 2005,(7): 631-633

[16] Ould-Cheikh-Mouhamedou Y. Crozier S, Kabal P. Comparison of Distance Measurement Methods for Turbo codes. In: Proceedings of the 9th Canadian Workshop on Information Theory, Montreal, Canada, 2005. 36-39

Shao Xia, born in 1970. She received her M.S. degree and B. S. degree from Zhengzhou University in 2007 and 1992 separately. Her research focuses on key techniques for telecommunication theory and engineering.

10.3772/j.issn.1006-6748.2015.03.010

①Supported by the National High Technology Research and Development Programme of China (No. 2014AA01A705) and the National Natural Science Foundation of China (U1204607).

②To whom correspondence should be addressed. E-mail: zhangweidang@zzu.edu.cn Received on June 23， 2014***