基于SimulationX的泵控马达调速系统建模仿真

　,

(江苏大学 汽车与交通工程学院， 江苏 镇江　212013)

引言

国外农用大功率拖拉机为了提高作业效率，降低劳动强度，适应工作负载频繁变化，多采用液压机械无级变速器(HMCVT)。液压机械无级变速器采用的是液压功率流与机械功率流组合传递的双功率流无级变速传动形式，既能实现较高的传动效率，又能实现无级变速，同时兼顾了液压系统良好的控制性[1]。HMCVT的传动效率是由机械效率和液压效率共同决定的，一般认为机械效率变化不大，则液压传动系统的效率变化影响整个传动系统的效率，研究液压系统的调速特性和效率对液压机械无级变速传动系统的性能研究有重要意义[2]。

目前已有的一些研究针对变量泵-定量马达容积调速回路的特性，也有针对伺服变量机构的动态特性[3-6]，但是对变量泵-马达系统与伺服变量机构结合进行的分析和研究很少见。由于变量泵输出流量的调节是由液压伺服机构来完成的，研究由液压伺服机构控制的变量泵-定量马达容积调速系统。

1　液压泵控马达调速系统的工作原理

液压泵控马达调速系统主要是由由变量泵-定量马达系统和伺服变量机构组成的，如图1所示。

系统通过控制信号驱动电液比例阀2， 改变阀芯的位移和方向，进而改变进、出液压缸3油液的流量和方向，改变活塞杆的位移，位移变化带动变量泵的斜盘倾角产生相应角度倾斜变化。进而调节变量泵1的排量变化，从而改变马达5的输出转速。

1.泵　2.电液比例阀　3.双作用液压缸　4.变量泵　5.定量马达　6、7.高压溢流阀　8、9、13.单向阀　10.减压阀　11、12.溢流阀图1　液压泵控马达调速系统原理图

2　液压泵控马达调速系统特性

用e=VP/VPmax表示变量泵流量的相对变化率，变化范围为[-1,1]。当e=0时，表示变量泵的斜盘没有倾斜，变量泵不排油，马达静止；当e=-1或+1时，表示泵的排量达到负的或正的最大值，推动马达转速达到负的或正的最大值。

由于泵和马达中的油液在较高压力下运转，必然存在泄漏，实际流量与泵和马达理论流量不同，即存在所谓的容积效率ηv；同时，由于油的黏性阻滞，负荷下的轴承的摩擦损失，即存在所谓的机械效率ηm;容积效率影响转速，机械效率影响转矩。则液压总效率ηt为：ηvηm,影响传动的效率，因此变量泵调速系统的基本特性，如表1所示。

表1　液压泵和马达的基本表达式

表中，下标P、M分别代表泵和马达；V是排量，cm3/r；n为转速，r/min；Δp为油液进出口的压差，MPa。

若忽略管路中压力损失，泵变量调速系统的流量平衡方程为：

QM=QP-CtΔp

(1)

将表1中的公式代入可求得：

nM=(enPVPmaxηvP-CtΔp)/VM

(2)

式中，Ct为液压泵和液压马达的总泄漏系数；

将表1中的马达转矩公式代入上式时，消去Δp：

MM=VMηmM(enPVPmaxηvP-VMnM)/(20πCt) (3)

定量马达的转矩随定量马达转速变化的曲线如图2所示。这是这是设定一定的泵转速的力矩转速曲线。

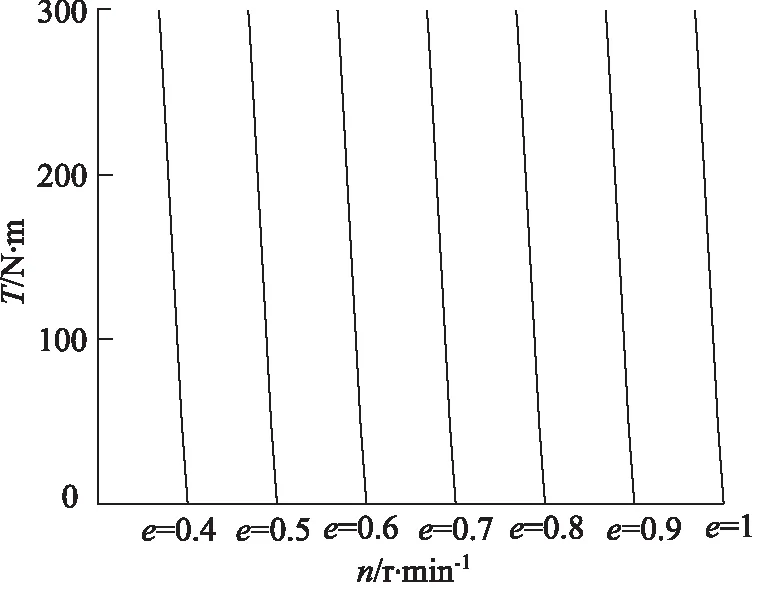
图2　马达输出的力矩-转速特性

从图2可以看出，当e为一定时，随着马达转速增大，马达输出力矩减小，不同的排量比e有不同的转矩-转速特性曲线，相互基本平行。图中的速度刚性为：

(4)

在此速度刚性的物理意义是：马达力矩因外负荷而改变时，系统所具有的阻止马达转速改变的能力，即曲线角度越是接近90°，系统压力因高压泄漏而对转速降低的影响越小，说明该系统变量泵调速系统的速度刚性较好。

3　液压泵控马达调速系统马达效率分析

由于泄漏，马达实际所需的流量大于理论流量，故马达的容积效率为：

(5)

其中，qm为马达的实际流量；qom为马达的理论流量；Δq=CsV·p/μ为泄漏量；Cs为漏损系数。

实际上，由于马达内有各种机械和液压摩擦损失，马达的理论转矩应大于实际转矩，故马达的机械效率为：

(6)

其中，Mm为马达的实际转矩；Mom为马达的理论转矩；

相互滑动的间隙油膜所造成的压力差p可表示为：

p=Cdμn

(7)

其中，Cd为黏阻系数；

马达内的转矩损失主要包括滑动表面摩擦力矩和轴承摩擦力矩，故液压马达的摩擦力矩ΔM为：

(8)

其中，常数Cd和Cf随马达的类型结构而异。

根据公式(6)～(8)可得出马达机械效率为：

(9)

根据公式(5)～(9)，可以获得泵控液压马达的效率曲线，其中，泵控马达的参数为：变量泵、马达的排量均为55 cm3/r，如图3～图6所示。

通过图3～图6可知：液压马达容积效率随着排量比的增大而增大，机械效率随着排量比的增加而降低；压差一定时，随着输入转速的增加，液压马达的机械效率降低，容积效率则增加；输入转速一定时， 液压马达的容积效率随着压差的增加而减少，机械效率随着压差的增加而增加。

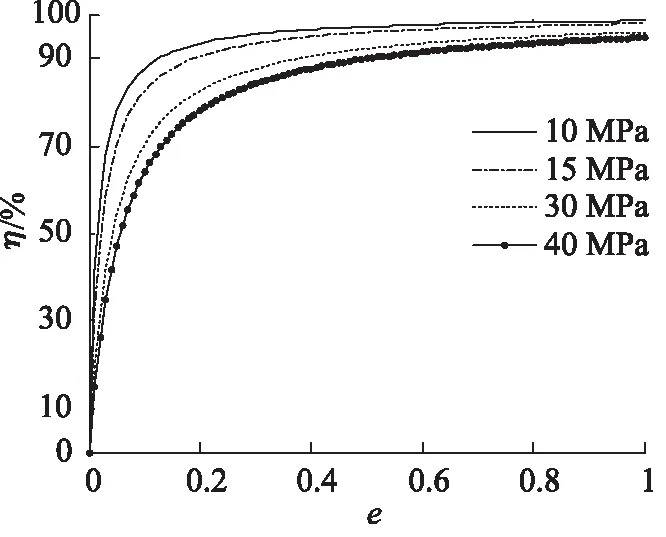
图3　不同压力马达容积效率随排量比变化曲线

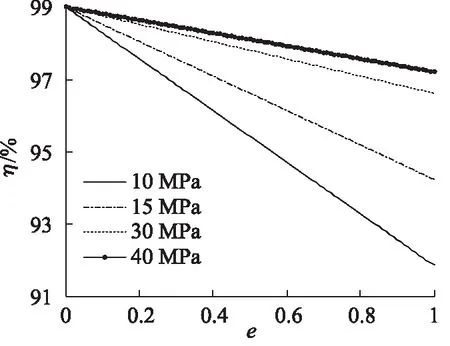
图4　不同压力马达机械效率随排量比变化曲线

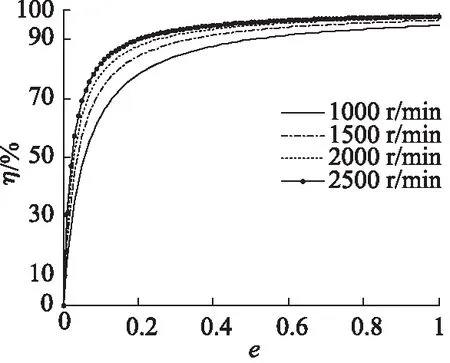
图5　不同转速马达容积效率随排量比变化曲线

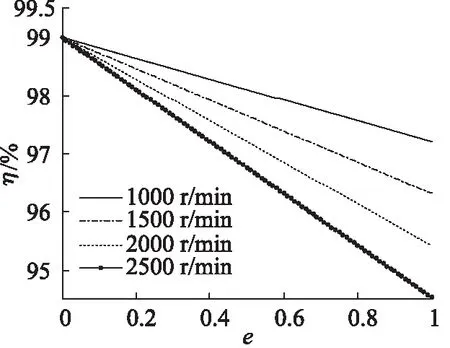
图6　不同转速马达机械效率随排量比变化曲线

4　液压泵控马达调速系统的动态仿真

为了验证不同参数对液压马达的效率的影响，利用ITISimulation X建立泵控马达调速系统的仿真模型，如图7所示。在图7中，模型采用了PID控制、速度反馈的闭环控制。变量机构的活塞位移采用位移传感器反馈到控制器，形成内部闭环反馈，控制泵的性能和精度；用转速传感器将马达转速反馈到控制器，形成外部闭环反馈，实现对马达转速的控制。

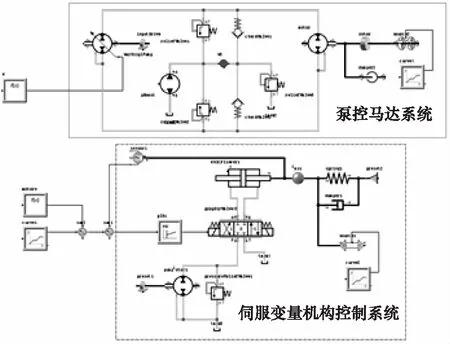
图7　泵控马达调速系统闭环仿真模型

4.1　液压泵控马达调速系统的仿真

参数设置：泵、马达的排量55 cm3/r；PID控制参数经过多次调整为：Kp=0.0008、Kd=0.001、Ki=0；伺服机构的外负载维持在100 N；泵和马达机械效率为90%的情况下仿真，分为以下几种情况：

(1) 仿真系统平缓加速或减速的情况下，PID控制对泵控马达系统的影响。参数设置：泵输入转速为2000 r/min、外负载力矩为100 N·m、马达目标转速在第3 s从600 r/min加速到1880 r/min，在第6～10 s保持匀速，第10～14 s减速，然后保持匀速。分别给出未加PID控制和加上PID控制器后的马达输出转速曲线，如图8所示。

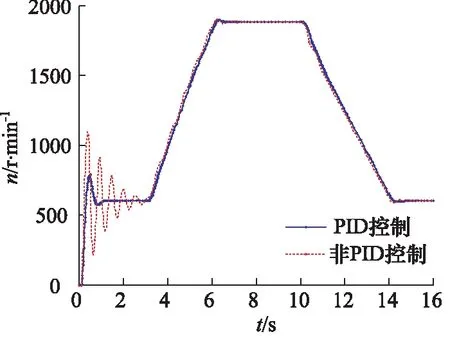
图8　马达输出转速仿真曲线

从图8可以看出：用PID控制后的马达转速的动态性能明显提高，在加速、匀速和减速段的超调量明显减少，稳态误差靠近零。系统响应时间短，大约0.8 s又趋于稳定值，系统稳定性较好，这种控制方式较可行。

(2) 仿真不同外负载冲击下对泵控马达调速系统的影响。参数设置为：泵输入转速为2000 r/min、马达目标转速为1000 r/min、初始外负载为50 N·m，在第4 s的加大小为150 N·m的外负载，在第10 s的加大小为300 N·m的外负载，在第20 s的加大小为400 N·m 的外负载转矩信号。分别给出了未加PID控制的直接响应和加上PID控制器后的系统输出转速曲线、转矩和效率曲线，如图9、图10所示。

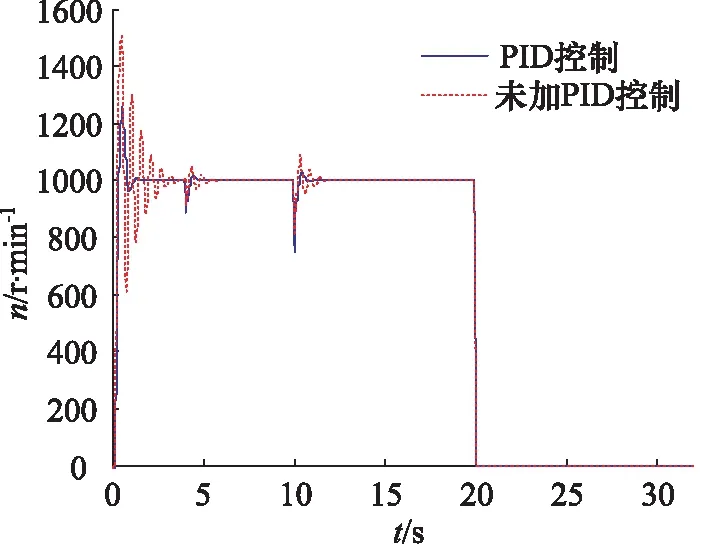
图9　加上外负载后马达输出转速仿真曲线

从图9可以看出：外负载在50～300 N·m变化时，经过PID控制后的系统调整时间较短，响应速度较快，超调量大大减少。从图9可以看出，由于外负载的扰动，马达的输出转速突然下降，由于系统的反馈作用，泵控马达系统经过0.7 s又重新达到稳定值，跟踪到系统的输入信号，在加入400 N·m的外负载后，马达转速降为零，说明系统超载，系统快速卸荷；从图9和10可以看出，负载变化引起马达输出转矩发生变化，马达转速基本不改变，与公式(4)相符。

图10　加上负载后马达输出转矩仿真曲线

(3) 仿真排量比变化对马达效率的影响。参数设置为：泵输入转速为2000 r/min、外负载分别为0和100 N·m； 输入马达转速在-2000 r/min到2000 r/min(排量比在-1到1)改变，给出了PID控制器后的马达效率曲线，如图11所示。

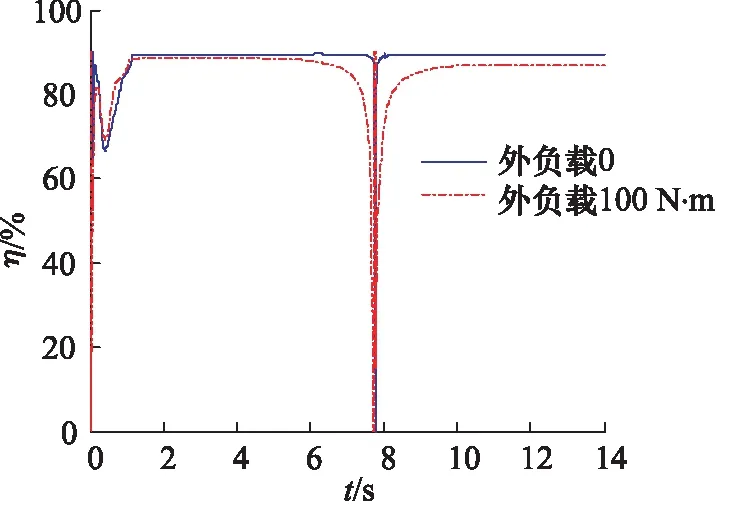
图11　排量比变化时马达输出效率仿真曲线

从图11可以看出：经过PID控制后，系统响应平稳。当排量比在-1到0变化时(0～8.7 s)，马达输出效率随着排量比的减小而降低；当排量比在0～1变化时(8.7～14 s)，马达输出效率随着排量比的增大而逐渐升高，当马达转速趋于稳定时，马达输出效率稳定不变；当外负载转矩为100 N·m时，马达输出效率明显降低。图中效率曲线均未通过零点(t=8.7 s)是由于系统泄漏现象的存在。

(4) 仿真外负载、输入转速对马达效率的影响。输入转速、外负载是影响效率的主要因素。因此，将外负载、泵输入转速与效率置于同一坐标系中，改变外负载和泵输入转速，记录不同情况下的马达输出效率，如图12所示。

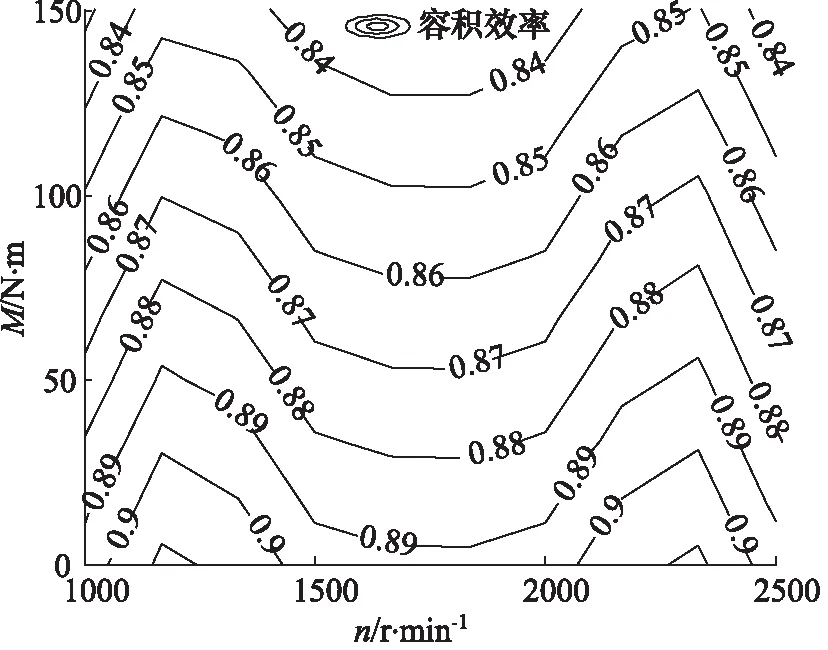
图12　马达目标转速为1000 r/min的容积效率

从图12中可以看出： ① 泵输入转速一定时，外负载越大，马达输出效率越低； ② 外负载一定时，随着变量泵输入轴输入转速的增加，马达输出效率整体水平上是逐渐提高的，当输入转速达到2000 r/min时，马达效率达到最高值。此后，输入转速持续增加时，马达输出效率有所减少。说明在一定输入转速范围内，输入转速与马达输出效率是成正比的。

5　结论

(1) 利用SimulationX建立了泵控马达液压调速系统的物理模型， 并对系统的动态响应特性进行了仿真。仿真结果表明系统加上PID控制后， 系统的超调

量和反应时间明显减小了，使系统的性能得到了很大的改善。另外，加上负载转矩后，系统能够很快跟踪到输入信号，实现马达恒转速输出，说明这个闭环系统有很强的抗负载干扰能力。

(2) 研究了转速、排量比以及外负载对马达效率的影响，得到了马达效率与影响参数的等高线图，可以直观地反映出马达效率与转速、外负载之间的关系与相互影响，仿真结果显示与理论推导相符。

参考文献：

[1]彭增雄，苑士华.液压泵控马达数字调速系统研究[J].北京理工大学学报，2009,(3):205-209.

[2]苑士华,魏超.液压机械无级变速器动态特性的影响因素研究[J].农业工程学报，2008:33-37.

[3]高翠.液压机械无级变速传动特性分析与仿真[D].镇江：江苏大学，2010:24-38.

[4]齐晓杰.汽车液压与气压传动(第2版)[M].北京：机械工业出版社，2011:39-50.

[5]白国林，王占林.变频调速：变量泵复合调节液压系统仿真研究[J].系统仿真学报，2006,(18):424-426.

[6]陈永新, 柯尊忠.四通阀控单出杆液压缸动态特性研究[J].机床与液压,2007:68-74.

[7]吕爱玲，姜友山，邹广德，等.全液压推土机液压驱动系统变量泵效率研究[J].农业装备与车辆工程，2010:11-15.

[8]Alarico Macor, Antonio Rossetti.Optimization of Hydro-mechanical Power Split Transmissions [J] .Mechanism and Machine Theory,2011.