基于中轴线的隧道点云去噪算法

程效军，贾东峰，刘燕萍，程小龙

（1.同济大学 测绘与地理信息学院，上海200092；2.同济大学 现代工程测量国家测绘地理信息局重点实验室，上海200092；3.同济大学浙江学院 土木工程系，浙江 嘉兴314051）

隧道作为城市交通的重要组成部分，由于受到周围土体的挤压、地上物体及地质运动的影响，存在一定程度的形变.这种形变如果超过一定限度会造成巨大的安全事故，因此需要对地下隧道进行定期监测，以排除安全隐患保证其安全运营.文献［1-3］讨论了摄影测量技术在隧道监测中的应用方案，但是由于隧道内部空间狭小，照明条件差，不利于立体像对的获取与形变分析.近年来一些基于光栅传感技术的隧道监测系统也比较广泛地应用在隧道监测中［4-6］，该系统可以精确地反映隧道局部区域的收敛变化，但是在监测中需要分断面大量布设光栅收敛计.此类方法的资金投入和时间消耗较大.Stephanie Fekete等［7］详细总结了点云数据在隧道竣工监测中的应用方案.Gikas［8］介绍了三维激光扫描仪在隧道施工阶段的应用方法，通过和传统方法的比较，分析了三维激光扫描技术在隧道监测领域的应用优势.Argüelles Fraga等［9］讨论了隧道尺寸、激光光斑、激光入射角及扫描分辨率对点云精度的影响.通过学者们的广泛研究，证实了三维激光扫描技术在隧道监测领域巨大的应用潜力.但是，一些隧道点云数据处理的关键问题，如隧道点云的去噪、点云中轴线的拟合等，在近年的研究文献中论述不多.隧道作为一个狭长密闭的空间，其内部的管壁附属物、粉尘以及测量人员产生的噪声需要予以剔除，否则影响隧道形变分析的精度.常用的点云去噪方法，如双边滤波算法［10-11］、平均曲率流滤波算法［12-13］、均值漂移算法［14-16］等，对狭长密闭空间的隧道点云去噪效果差且容易破坏原始数据的精度.一些交互式的手工去噪方法也无法有效地深入到点云内部进行噪声去除.因此提出一种稳健的隧道点云去噪方法，对三维激光扫描技术在隧道监测中的应用具有重要意义.Han等［17］通过将隧道点云投影到水平面上，并将投影后的点云转化成平面二值影像，采用数字图像处理中的骨架提取算法实现了平面点云的骨架（中轴线）提取.KANG Zhizhong等［18］采用类似的平面投影方法将三维隧道点云转化成二维平面数据，然后通过随机采样统计算法对二维平面点云进行分段曲线拟合，以最终的拟合曲线作为隧道点云的中轴线，并实现对隧道的收敛分析.上述基于点云投影的方法可以快速生成点云的中轴线，但是仅将点云投影到单一平面，未考虑到点云在高程方向上的变化，生成的中轴线和实际的中轴线偏差较大.

许多学者对散乱点云的轴线拟合进行了研究，其中Lee［19］提出了基于改进的移动最小二乘曲线拟合算法，其方法可以扩展到多维空间数据的曲线拟合中.WANG Wenping等［20］采用B样条曲线去拟合平面散乱点集（含有噪声），提出了平方距离最小原则，用以衡量数据拟合的精度.ZHANG Mei等［21］提出了基于二次B样条曲线的点云拟合方法，通过改进的基于时间优化的二次B样条曲线避免高阶曲线拟合中的摆动问题.ZHANG Wenyang［22］讨论了局部多项式拟合在半变系数模型中的应用.Stephem等［23］提出了简化的多项式拟合方法，采用三阶多项式拟合含有噪声的数据点集，达到了预期效果.

针对上述点云去噪方法以及中轴线拟合方法的讨论，本文提出一种基于隧道中轴线的点云去噪方法.建立了点云双向投影模型，并通过高阶多项式进行中轴线拟合，同时根据给定的距离阈值实现隧道内部噪声的去除.为了证实文中方法的可行性及准确性，本文通过模拟一段隧道点云数据（其中轴线已知），用以分析中轴线拟合的精度和高阶多项式的次数.同时对某实际长距离隧道点云数据进行去噪，证实该方法的可行性.本文研究的隧道类型主要为衬片结构的盾构隧道.通过中轴线去除原始点云内部的噪声，为后期二次中轴线拟合与隧道收敛分析提供高质量的输入点云.

1 隧道中轴线的计算

1.1 双向投影

根据隧道点云的空间特点，将其分别向xOy，xOz两个平面方向投影，称其为双向投影.其中，x轴正方向为隧道起始端到末端的连接方向，水平面上垂直于x向为y轴方向并按右手系确定其正方向，z轴垂直于xOy面向上为其正方向.图1为对隧道点云进行双向投影.图中，空间点云数据用黑色表示，灰色数据分别是投影到xOy平面和xOz平面的点云.通过点云的双向投影可以明显地反映出隧道在水平和垂直方向上的变化.

图1 隧道点云的双向投影Fig.1 Bilateral projection of tunnel point cloud

1.2 栅格采样

对于投影后的海量点云数据，直接对其进行曲线拟合影响数据计算的效率.由于投影后的隧道点云形状规则、边界特征明显，同时数据密度均匀，可以有效降低拟合过程中的姿态摆动问题.因此，采用均匀栅格压缩算法对点云进行均匀采样以降低密度提高数据拟合效率.首先基于点云的密度设置栅格边长，同时由于边界点在数据拟合中的重要性，采样中保留首末栅格内的点，对2到N-1栅格进行采样（N为栅格编号），并根据压缩比设置采样间隔，完成平面点云的重采样.

1.3 基于多项式的数据拟合

由于平面点云曲率变化平缓，拐点较少，适合采用多项式拟合对其进行数据拟合.多项式拟合的基本原理如下：

假设给定数据点（xi，yi）（i=1，2，…，m），Φ为所有次数不超过n（n≤m）的多项式构成的函数类，现求，使得

当n≥2满足式（1）的pn（x）称为最小二乘多项式，特别地，当n=1，称为最小二乘拟合.可根据多元函数求极值的必要条件

求取pn（x）的平方误差

结合式（2）可得

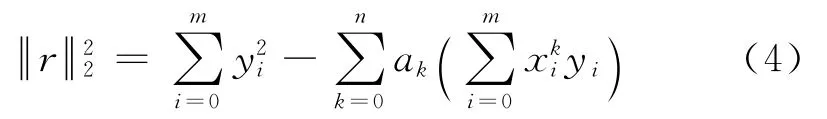
在平面点集的多项式拟合过程中，次数n的选择决定着拟合精度和效率.通过对模拟隧道数据以及真实隧道数据的试验发现，6次、7次多项式拟合可以满足隧道点云拟合的精度和效率.

1.4 多项式插值

通过多项式拟合可以生成平面xOy，xOz上的曲线，通过x轴坐标可以建立两条曲线的映射关系.根据曲线长度和曲率，对中轴线进行初步插值，初步插值点数可根据需要设定（本文取值100）.通过x轴坐标均匀采样100个点，并根据曲线方程，计算y，z坐标值，获得初始中轴线控制点.

1.5 局部加密

对于曲率变化较大区域，需进一步加密细化才能精确反映曲线形状.本文采用的加密细化原则是根据空间直线的夹角判断局部区域的曲率，如果两条空间直线的夹角大于给定角度阈值，则对构成空间直线的点位区间均匀插值，然后再次判断插入点后的相邻线段间的夹角，直至相邻线段间夹角小于给定角度阈值α.可根据以下经验公式确定角度阈值α的取值范围：

式中：D为控制点间的最大距离；δ为最大距离处垂直方向误差.本文控制点间最大距离为10m，由于入射角度影响在10m处的垂直方向误差为cm级.因此文中角度阈值α取为0.1°.最终连接所有插值点逼近表达中轴线.判断两条空间直线夹角的公式如下：

设空间直线L1的方程

直线L2的方程

则两空间直线方向矢量的夹角θ为

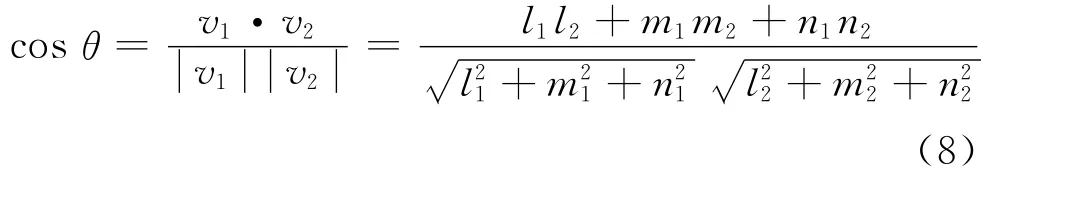
2 基于中轴线的点云去噪

2.1 根据中轴线控制点对隧道点云进行分块

首先根据插值后的中轴线控制点分割点云.如图2所示，pn，pn+1是中轴线上两点，计算过pn且法向量为vn的切平面ln，同时计算过pn+1且法向量为vn+1的切平面ln+1.切平面ln与ln+1可实现对区域点云的分割.同理，计算其他各中轴线点处的切平面方程，实现对整体点云的分块划分.其中按x轴坐标对控制点进行排序确定首点.

图2 基于中轴线点的点云分割Fig.2 Point cloud segmentation based on control points of centerline

2.2 基于距离阈值点云去噪

对于地下隧道，尤其是盾构隧道，其管片半径是固定值.以上海地区的地下隧道为例，其隧道设计半径为2.75m，轨道面至中轴线的最短距离是2.15 m.图3所示为盾构隧道设计断面参数.已知隧道的设计半径，考虑到管片存在变形，可给定距离阈值对点云内部噪声进行删除，通过本文试验分析，距离阈值区间为 ［2.65，2.75］ ，取2.70m可有效剔除管壁附属管线、支架、机电箱以及其他内部噪声，同时不破坏管壁点云数据.

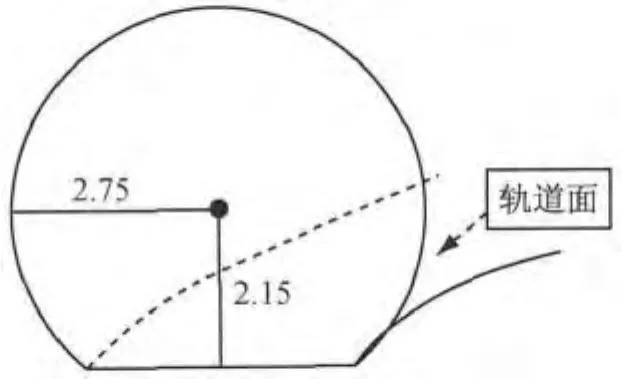
图3 隧道设计半径（单位：m）Fig.3 Design radius of tunnel（unit：m）

对于空间中任意一点p（xn，yn，zn）到空间直线L的距离可根据文献［24］进行计算.可求得L与平面的交点pt（xt，yt，zt），求取即为p到空间直线L的距离.判断其与给定距离阈值的大小，如果小于给定的距离阈值，则认为该点为噪声点，予以删除.根据上述方法，可以有效剔除隧道点云内部的噪声.

3 实例分析

为了验证上述方法的可行性和精确性，本文采用两组试验数据进行分析.一组数据是模拟数据，通过隧道的设计参数模拟生成隧道模型并插值生成隧道的点云数据，其隧道中轴线已知.该组模拟数据长度为500m，高差为5m.第二组数据是采用地面三维激光扫描仪采集的某地铁隧道的点云数据，共采集47站数据，长度约为1 000m，高差约为3m.

3.1 模拟点云数据分析

在隧道的设计过程中，为了保证地下交通运行的安全，其曲率变化在一定的缓和度内.根据此特点，模拟隧道在水平方向存在较大角度的缓慢转折，其隧道半径为2.75m，轨道面距离中轴线2.15m.图4为模拟隧道及其中轴线.

图4 模拟隧道Fig.4 Simulated tunnel

3.1.1 模拟隧道数据分析

将该段模拟点云数据分别向xOy，xOz平面投影，获得隧道在水平和垂直方向的平面点云，图5为模拟点云数据的双向投影.

采用栅格压缩算法对其进行均匀采样简化，简化后点的数量为10 000.同时根据多项式拟合方法对投影到平面的点云进行拟合.为了分析多项式次数对数据拟合精度的影响，确定合适的拟合次数，本文分别采用4，5，6，7，8，9次多项式对水平面点云进行拟合.表1是对水平面点云进行拟合后的曲线方程参数.

图5 模拟隧道点云双向投影Fig.5 Bilateral projection of simulated tunnel point cloud

图6为不同次数的多项式方程曲线，其中曲线编号表示该曲线的次数.为了分析拟合精度，分别提取不同曲线同一位置处的坐标值并与已知中轴线进行比较.表2为在x轴-150，0，150处不同曲线的坐标值.通过与已知值比较，图7a中反映了5，6，7，8次曲线在x=-150，0，150时对应y值的偏差.从图中可以看出6，7次多项式方程在不同位置处的偏差较小且均匀，5次曲线的拟合偏差较大且不均匀.图7b显示了不同次数曲线的拟合精度，通过对不同点位误差统计分析显示7次多项式拟合的点位精度最高（本次试验中）.同样，对垂直面的拟合数据显示在本例中7次多项式精度也最高.

图6 不同次数多项式曲线（单位：m）Fig.6 Polynomial curve of different times（unit：m）

3.1.2 中轴线精度分析

采用7次多项式拟合，分析两条中轴线上相同位置处的y，z轴坐标偏差.图8a为水平方向偏差.对于高阶多项式拟合，其数据首、末端容易出现摆动，并且对于拐点过多的曲线，在其拐点处随着多项式阶数的增加会产生剧烈摆动.从图8a可以看出，由于多项式的摆动，其首、末端的水平偏差较大，分别为12.6mm与10.1mm；其他点位处的最大误差是3 9号点的9.6mm，最小误差是1 0 9号点的0.2 mm，水平方向所有点位偏差的中误差为5.3mm.

垂直方向的偏差分析.图8b显示了控制点在z轴（垂直）向的偏差.同样由于高阶曲线的摆动造成首末点位的偏差较大，分别为18.0mm与16.8 mm.其他点位处最大误差是44号点的13.0mm，最小误差是12号点的1.3mm，垂直方向所有点位偏差的中误差为9.2mm.

通过上述分析可以看出，采用7次多项式拟合曲线水平方向的偏差优于垂直方向的偏差.可以通过数据分段来提高垂直方向曲线拟合的精度.

表1 不同次数多项式拟合水平面点云的方程参数Tab.1 Parameters of equations of horizontal point cloud fitted by different polynomial times

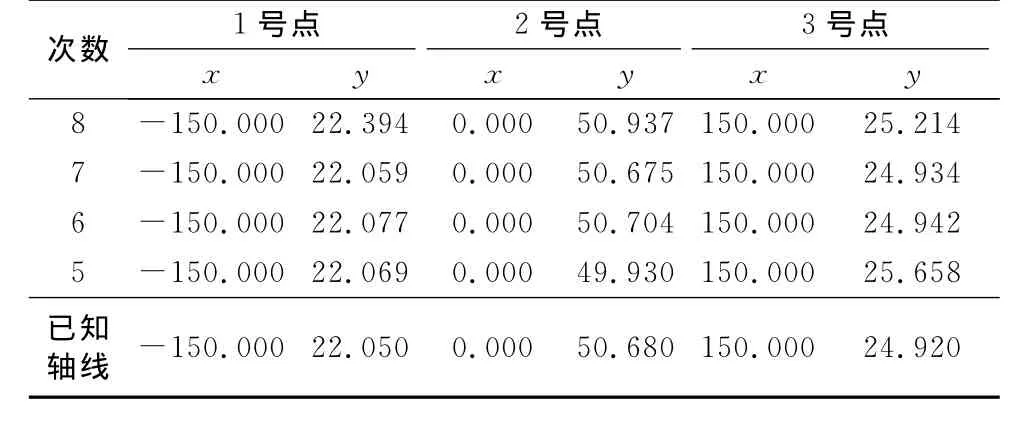
表2 不同曲线点位坐标计算Tab.2 Coordinates computation of different curves

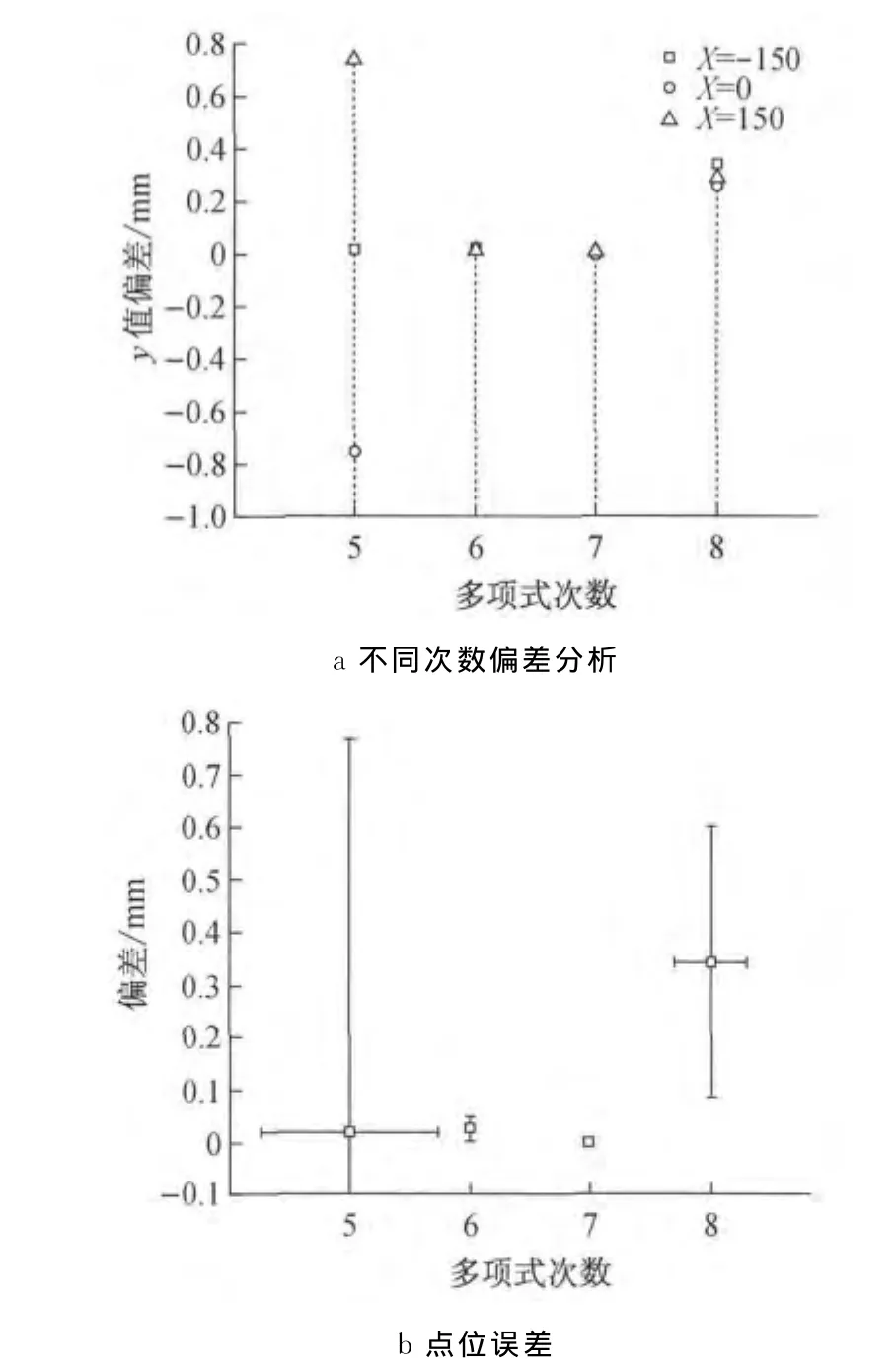
图7 不同次数的y值偏差与点位误差分析Fig.7 Error analysis of y value discrepancy of different times and points

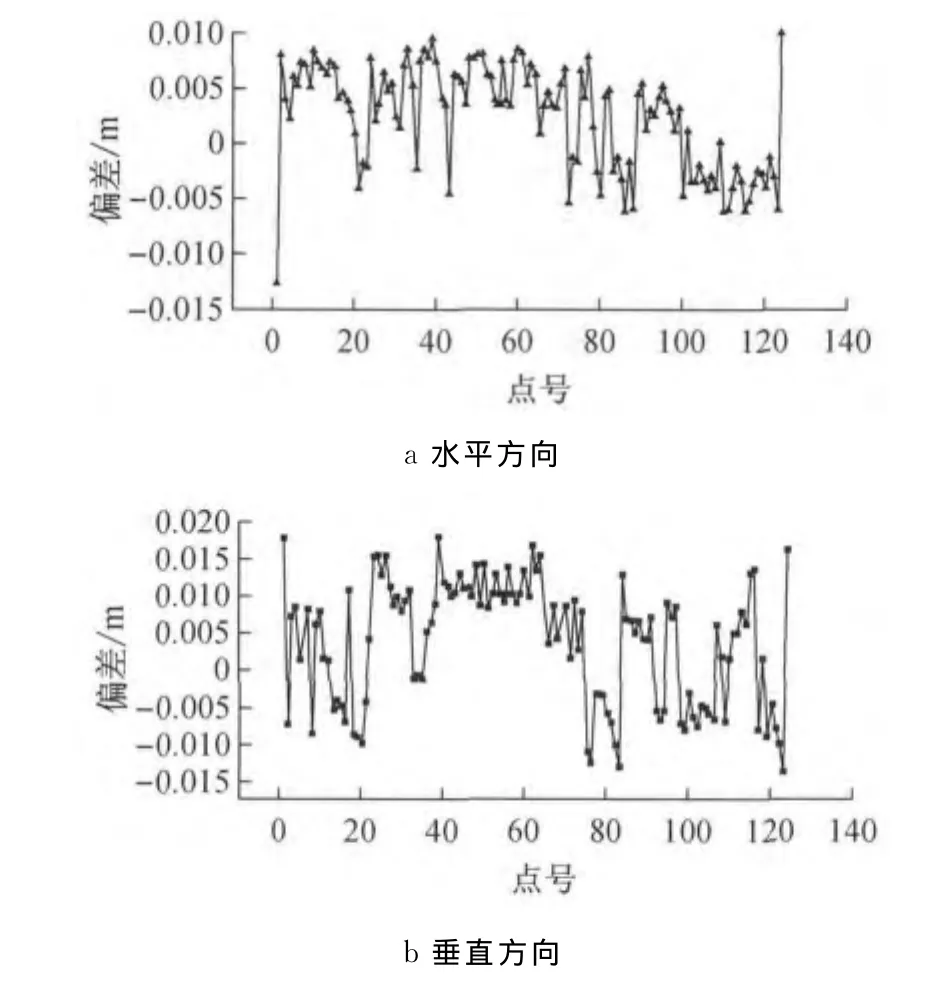
图8 水平、垂直方向偏差分析Fig.8 Deviation analysis

3.2 实际点云数据分析

3.2.1 点云数据

对上海某运营地铁线路进行数据采集，共采集47站点云数据，每站长度约25m.配准后的点云数据约1 000m，高差约为3m，点个数为10 005 476.同样地，采用栅格压缩方法对投影后的平面点云数据进行均匀采样压缩，以减少数据量提高多项式拟合的效率.采用7次多项式对点云进行拟合，拟合的多项式方程分别为

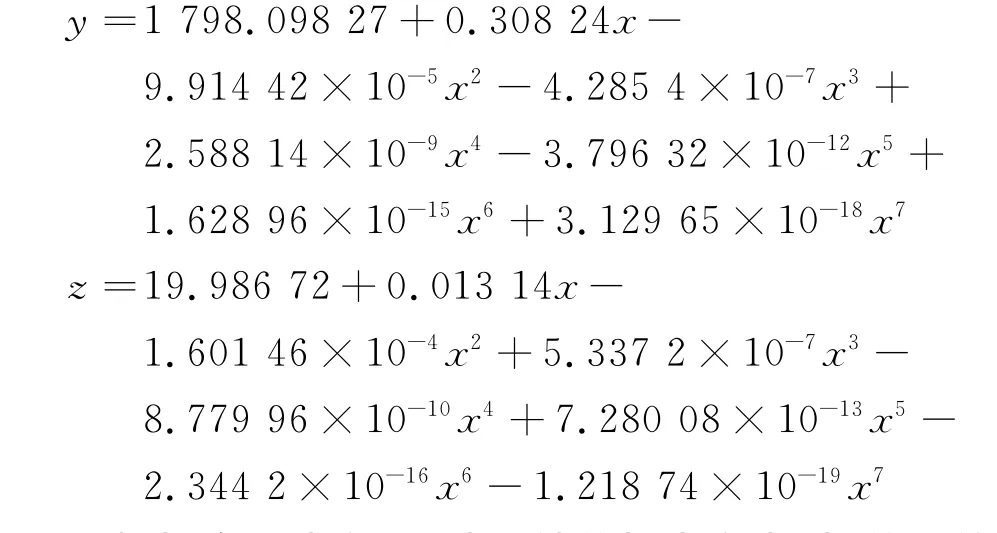
根据多项式方程，以x轴数据为参考，插值初始中轴线控制点，并根据相邻空间直线间夹角≤0.1°的原则进行控制点加密，加密后的控制点如图9a所示，共164个点.采用直线段对控制点进行连接，构成点云的中轴线.连接后的中轴线如图9b所示.

图9 中轴线拟合Fig.9 Centerline fitting

3.2.2 基于中轴线的隧道点云去噪

基于本文提出的方法，通过对隧道点云数据分块.计算各控制点处的切平面实现对点云数据的划分.图10为实际隧道点云数据内部的噪声数据，主要包括管线噪声、内部粉尘噪声和工作人员噪声.

图10 隧道点云内部噪声Fig.10 Internal noise data of tunnel point cloud

基于加密后的控制点将点云划分为163个区间.给定距离阈值为2.70m，通过计算区间内点到直线的距离，判断与给定距离阈值2.70m的大小进行噪声点的剔除.图11为局部区域的点云去噪.图11a是点云数据左侧某断面图，图中含有管线噪声.图11b是点云数据中部某断面图，图中含有管线及测量人员噪声.图11c是某段大曲率点云区间.通过计算点到中轴线的距离进行噪声点的剔除.图11d是图11a噪声去除后的效果，图11e是图11b噪声去除后的效果，图11f是图11c噪声数据去除后的点云.图12为去噪后的隧道模型.采用透视模式显示点云去噪后的效果.其中图12a为某隧道单站扫描数据（约20m）的去噪效果图，图12b为某隧道10站（约200m）扫描数据的点云去噪效果图；图12c为某隧道50站（约1 000m）扫描数据的点云去噪效果图.通过对不同区域不同长度的盾构类型隧道进行测试，可以看出采用本文提出的方法可以有效去除隧道内部的噪声.

图11 局部区域的点云去噪Fig.11 Local point cloud denoising

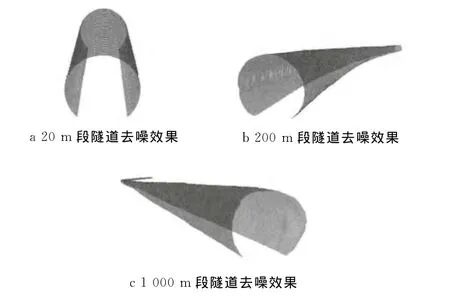
图12 去噪后的隧道点云模型Fig.12 Tunnel point cloud model after data denoising

4 结论

基于中轴线的隧道点云去噪，可以有效去除点云内部的噪声数据.通过计算点到中轴线的距离，可以准确去除隧道点云内部的噪声，提高点云分析的精度.隧道点云中轴线是一条空间曲线，在隧道中轴线的计算过程中需要考虑水平和垂直方向的变化；同时采用高阶多项式拟合可以有效地插值出满足去噪精度需要的点云中轴线，根据隧道曲率变化缓慢的设计特点，可采用高阶多项式拟合水平和垂直方向曲线并插值加密中轴线控制点用以表达中轴线；同时通过栅格压缩对投影后的点云均匀采样，可有效避免高阶多项式的局部摆动.

该方法会造成轨道面数据的删除，由于删除轨道面数据不影响后期的收敛分析，因此可以采用本文方法进行隧道点云去噪.如需保存轨道面数据，可通过计算轨道面与中轴线的夹角，对夹角内的点云进行过滤和删除，以保存轨道面数据点.进一步的研究方向是采用中轴线进行隧道点云的收敛分析，考虑点云数据投影后的分段拟合，采用多条曲线方程拟合插值中轴线，进一步提高中轴线的拟合精度.

［1］ Sasama H，Ukai M，Ohta M，etal.Inspection system for railway facilities using a continuously scanned image［J］.Electrical Engineering in Japan，1996，125：1345.

［2］ Paar G，Kontrus H.Three-dimensional tunnel reconstruction using photogrammetry and lasers scanning［C］∥Proceedings of the 3rd Nordost.Berlin：IEEE，2006：1231-1244.

［3］ Wang T T，Jaw J J，Hsu C H，etal.Profile-image method for measuring tunnel profile-improvements and procedures［J］.Tunnelling and Underground Space Technology，2010，25：78.

［4］ 赵星海，邱海涛.光纤Bragg光栅传感技术在隧道监测中的应用［J］.岩土力学与工程学报，2007，26（3）：587.ZHAO Xinghai，QIU Haitao.Application of fiber bragg grating sensing technology to tunnel monitoring［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（3）：587.

［5］ 丁勇，施斌，隋海涛.隧道结构健康监测系统与光纤传感技术［J］.防灾减灾工程学报，2005，25（4）：375.DING Yong，SHI Bin，SUI Haitao.Tunnel structural health monitoring system and fiber optic sensing technology［J］.Journal of Disaster Prevention and Mitigation Engineering，2005，25（4）：375.

［6］ 施斌，徐学军，王镝，等.隧道健康诊断BOTDR分布式光纤应变监测技术研究［J］.岩土力学与工程学报，2005，24（15）：2622.SHI Bin，XU Xuejun，WANG Di，etal.Study on BOTDR-based distributed optical fiber strain measurement for tunnel health diagnosis［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（15）：2622.

［7］ Fekete S，Diederichs M，Lato M.Geotechnical and operational applications for 3-dimensional laser scanning in drill and blast tunnels［J］.Tunnelling and Underground Space Technology，2010，25：614.

［8］ Gikas V.Three-dimensional laser scanning for geometry documentation and construction management of highway tunnels during excavation［J］.Sensors，2012，12（8）：11249.

［9］ Argüelles-Fraga R， Ordóñez C， García-Cortés S，etal.Measurement planning for circular cross-section tunnels using terrestrial laser scanning［J］.Automation in Construction，2013，31：1.

［10］ Jones T.Feature preserving smoothing of 3D surface scans［D］.Cambridge：Massachusetts Institute of Technology，2003.

［11］ Fleishman S，Drori I，Cohen-Or D.Bilateral mesh denoising［J］.ACM Transactions on Graphics，2003，22（3）：950.

［12］ Desbrun M，Meyer M，Schroder P，etal.Implicit fairing of irregular meshes using diffusion and curvature flow［C］∥Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques.Los Angeles：ACM Press，1999：317-324.

［13］ Vollmer J，Mencl R，Muller H.Improved laplacian smoothing of noisy surface meshes［J］.Computer Graphics Forum，1999，18（3）：131.

［14］ Georgescu B，Shimshoni I，Meer P.Mean shift based clustering in high dimensions：A texture classification example［J］.Computer Vision，2003（1）：13.

［15］ Comaniciu D，Meer P.Mean shift analysis and applications［J］.Computer Vision，1999（2）：1197.

［16］ Comaniciu D，Ramesh V，Meer P.The variable band width mean shift and data-driven scale selection［J］.Computer Vision，2001（1）：1638.

［17］ Han S，Cho H，Kim S，etal.Automated and efficient method for extraction of tunnel cross sections using terrestrial laser scanned data［J］.Journal of Computing In Civil Engineering，2013，27（3）：274.

［18］ KANG Zhizhong，ZHANG Liqiang，LEI Tuo，etal.Continuous extraction of subway tunnel cross sections based on terrestrial point clouds［J］.Remote Sensing，2014，6：857.

［19］ Lee I K.Curve reconstruction from unorganized points［J］.Computer Aided Geometric Design，2000，17：161.

［20］ WANG Wenping，Pottmann H，LIU Yang.Fitting B-spline curves to point clouds by curvature-based squared distance minimization［J］.ACM Transactions on Graphics，2006，25（2）：214.

［21］ ZHANG Mei，YAN Wei，YUAN Chunming，etal.Curve fitting and optimal interpolation on CNC machines based on quadratic B-splines［J］.Science China Information Sciences，2011，54（7）：1407.

［22］ ZHANG Wenyang，Lee S，SONG X.Local polynomial fitting in semivarying coefficient model ［J］.Journal of Multivariate Analysis，2002，82：166.

［23］ Stephem S K，Nagi N.A simplified polynomial-fitting algorithm for DAC and ADC BIST［C］∥Proceedings of Test Conference.Washington D C：IEEE，1997：398-395.

［24］ 同济大学应用数学系.高等数学（上册）［M］.5版.北京：高等教育出版社，2001：334.Department of Applied Mathematics of Tongji University.Higher mathematics（first volume）［M］.5th ed.Beijing：Higher Education Press，2001：334.