Q690D高强钢箱形截面柱的滞回性能

陈素文，陆志立，陈 星，李国强

（1.同济大学 土木工程防灾国家重点实验室，上海200092；2.同济大学 土木工程学院，上海200092）

随着高强度钢材在建筑工程和桥梁工程中的广泛应用［1］，对于高强钢的研究逐渐成为了热门课题.目前国内外对于Q460高强度钢材的材料性能以及构件的受力性能已有较为系统的研究.已有研究表明：①随着钢材强度的提高，伸长率下降，屈强比明显增大，延性降低；②试验量测结果［2-6］表明，与普通钢构件相比，高强钢构件的截面焊接残余应力分布和数值相差不大，但残余应力与钢材强度的比值要小很多［2-9］；③相比普通钢构件，残余应力对高强钢构件的承载力影响较小，按现行规范的公式计算较保守［2-4，10-14］；④表明Q460高强钢 H形及箱形压弯构件具有很好的耗能能力和抗震性能［15-18］.李国强等［17］还提出了Q460C高强钢焊接H形和箱形截面柱的弯矩-曲率滞回模型.

但目前为止，国内外对于Q690高强钢柱的滞回性能研究较少，为此本文完成了两个Q690D高强钢焊接箱形截面柱的低周反复加载试验和数值模拟，研究轴压比、构件长细比和壁板宽厚比对高强钢柱滞回性能的影响.提出Q690D高强钢焊接箱形截面柱的弯矩-曲率滞回模型，为Q690高强钢结构的弹塑性地震反应分析提供依据.

1 试验简介

1.1 试件设计

试验试件钢材取自河南舞阳钢铁厂生产的16 mm厚Q690D钢板，根据《建筑抗震设计规范（GB 50011-2010）》［19］（以下简称《抗规》）中压弯钢构件长细比、壁板宽厚比的限值规定，按照钢材牌号修正后，得到各抗震等级下Q690高强钢压弯构件长细比及壁板宽厚比限值，并根据试验机加载能力设计试件信息如表1所示.表中，D，t分别为箱形截面宽度、壁板厚度，L0为悬臂柱计算长度（柱净高2 450 mm，加劲肋高度300mm，上端板厚100mm，加载头销轴中心至上端板距离255mm，如图1a所示），h0／t为箱形截面壁板宽厚比，λ为主轴长细比，n为名义轴压比，取为0.35.试件制作均采用火焰切割的16 mm厚Q690D钢板，加工采用CO2气体保护焊，焊接形式采用单坡口对接焊，焊丝选用与之匹配的ER110S-G型高强焊丝.

1.2 加载装置

试验采用同济大学建筑工程系结构试验室10 MN大型多功能静电液伺服加载系统进行.在水平地震作用下，框架柱轴力变化不大，而弯矩随地震作用发生周期性变化，可以假设其反弯点在柱的跨中，进而将框架柱简化为一端刚接另一端自由的悬臂柱，加载示意如图1a所示.图中，F为柱反弯点处水平剪力，N为柱中轴向压力.试验试件采用悬臂柱加载方式，柱底设置刚性底座模拟刚接，柱顶采用销轴连接模拟自由端，通过L形连杆分别与试验机竖向作动器及水平作动器相连，如图1b所示.

表1 箱形截面柱试件信息Tab.1 Dimensions of box-section specimens

图1 试验加载简介Fig.1 Introduction to test load

1.3 加载制度

试验与有限元分析的加载制度根据《建筑抗震试验方法规程（JGJ 101-96）》［20］中的规定，采用力和位移双重控制加载方式：①竖向加载采用力控制方法，根据试件轴压比大小，将竖向轴压力均匀加载至柱顶加载顶板上；②在保持竖向轴压力不变的情况下，对柱顶节点施加水平往复荷载.水平往复加载采用位移控制方式.取使构件边缘纤维进入屈服状态时的水平位移dy作为位移荷载增量，分别以±0.5dy，±dy，±2dy，±3dy，±4dy作为加载级别.第一级位移循环1圈，从第二级开始，每级位移循环3圈，如图1c所示，直至荷载下降至最大荷载的85%以下，认定构件破坏.

1.4 测点布置

试件位移计及应变片布置如图2所示，共布置26个位移计、24个应变片和4个应变花.

应变片及应变花布置于：①距试件顶板300mm位置，监测加载过程中试件弹性段的应变值；②距柱底250mm（截面高度）范围内等距布置3层应变片，用于监测柱底截面应变值，以及估测柱底曲率.位移计1，2用于测量加载头销轴位置平面内的绝对位移；位移计3，4用于测量悬臂柱顶板位置平面内的绝对位移；位移计5用于监测悬臂柱顶板与加载头平面内的相对滑移；位移计6用于监测悬臂柱顶板位置平面外的绝对位移.位移计7～24用于估测柱底曲率；位移计25用于监测刚性底座变形；位移计26用于监测刚性底座平面内滑移.

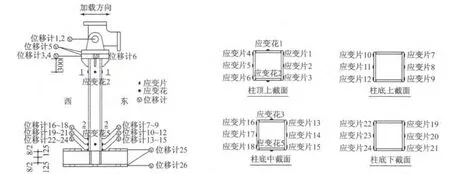
图2 箱形截面试件测点布置图（单位：mm）Fig.2 Measurement set-up for box-section specimens（unit：mm）

2 有限元模型

2.1 模型说明

本文采用软件ANSYS建立有限元模型.选用SOLID 185单元，该单元为三维8节点实体单元，每个节点有3个沿着x，y，z方向的平动自由度，可模拟超弹性、应力钢化、蠕变、大变形和大应变等.

有限元模拟采用悬臂柱加载方式，见图3，4.图中，M为柱底弯矩，θ为层间位移角.模型底部固接，顶部设置刚性加载板，竖向轴压力以集中荷载的形式作用于顶部加载板上，水平荷载加载于刚性加载板中心，并沿试件截面主轴方向进行水平往复加载.试验中因箱形试件沿两主轴方向初弯曲过大，在柱底500～1 000mm范围内进行了火焰矫正，加载时发现火焰矫正对钢材材料性能产生较大的影响.因此，在进行有限元模拟时，考虑了火焰矫正的影响，根据试件的实际火焰矫正位置，建立有限元模型，如图5所示.图中深色区域即为试件火焰矫正区域.

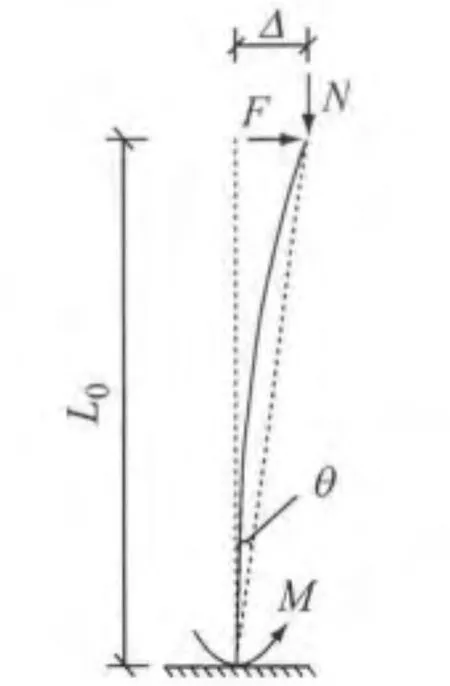
图3 试件受力原理图Fig.3 Schematic diagram of loading

图4 有限元模型Fig.4 FE Model

图5 试件B -1有限元模型Fig.5 FE model of specimen B-1

2.2 材料应力-应变关系

有限元分析采用Von-Mises屈服准则以及相关流动法则，材料模型采用多线性随动强化模型，并在模型中的火焰矫正区域定义其材料性能为经火焰矫正后的材料性能.模型中Q690D高强钢火焰矫正前后钢材的弹性模量E、屈服强度fy、抗拉强度fu、屈强比fy／fu、极限应变εu列于表2中，材料应力-应变曲线如图6和图7所示.

2.3 残余应力的影响

为了研究残余应力对箱形截面试件滞回性能的影响，参考班慧勇等提出的Q690高强钢焊接箱形截面残余应力简化模型［7］，模拟分析了试验试件B -1的全过程响应.有限元模型残余应力分布如图8所示，分别进行了施加与不施加残余应力的有限元分析，并提取试件M-θ骨架曲线进行对比，对比结果如图9所示.图中Mp为按理想弹塑性计算的全截面塑性弯矩.可以发现，残余应力对于试件的极限承载力影响很小，但由于残余应力的存在，试件提早进入非线性，试件刚度有所削弱.

表2 材料性能Tab.2 Mechanical properties

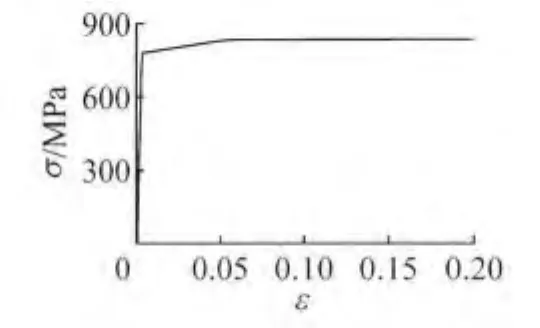
图6 Q690D高强钢材料模型Fig.6 Mechanical property model of Q690DHSS

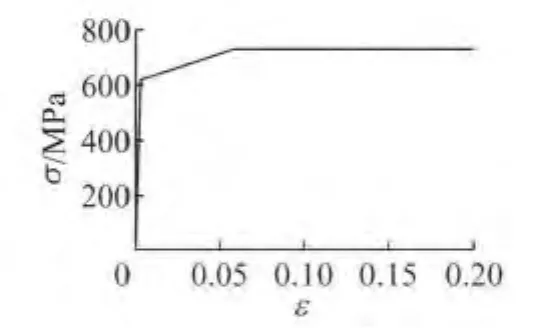
图7 火焰校正后钢材材料模型Fig.7 Mechanical property model of Q690DHSS after flame straightening

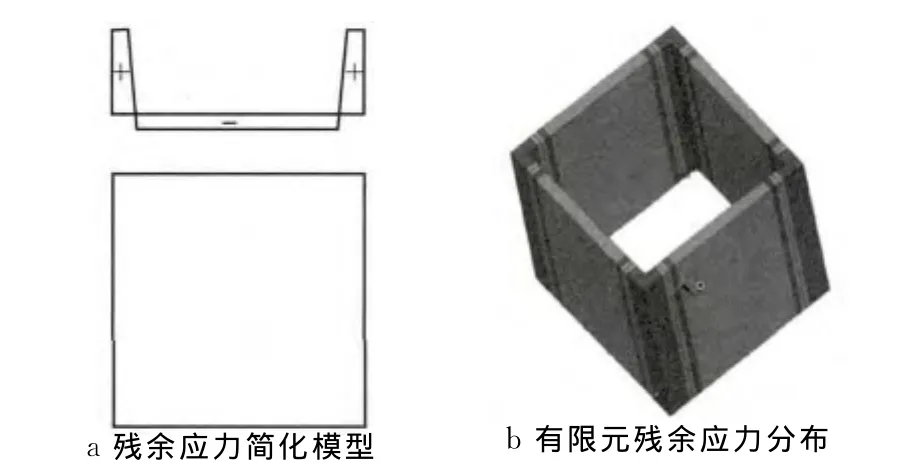
图8 箱形截面残余应力分布Fig.8 Residual stress of box-section

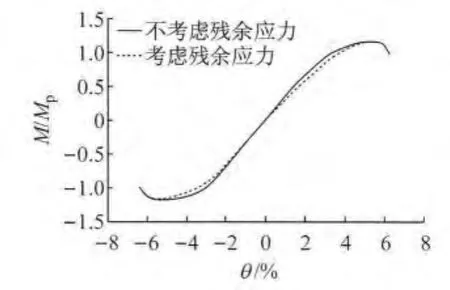
图9 残余应力影响Fig.9 Influence of residual stress

3 试验与有限元结果分析

如前所述，有限元模拟时考虑了火焰矫正对材料性能的影响及残余应力的影响.由图10可以看出，数值模拟与试验试件的破坏形态吻合较好，有限元模型能够较准确地模拟出试件局部失稳的位置及变形大小.

图10 试验与有限元破坏形态对比（试件B -2）Fig.10 Failure modes comparison of FE analysis and experimental results

从图11～13试验与有限元的对比可以看出，有限元分析得到的滞回曲线和骨架曲线与试验曲线在承载力、刚度以及滞回曲线的面积等方面都吻合较好，Q690D高强焊接箱形截面柱的滞回曲线爆满，耗能能力良好.不过，试验得到的M-θ滞回曲线刚度比有限元分析结果要小一些，这主要由以下3个方面原因造成：一是试验中试件柱脚不能达到理想刚接；二是试验加载头耳板与销轴之间存在微小间隙，加载过程中两者之间略有滑移；三是ANSYS有限元模拟构件滞回时，没有考虑反复加载中的刚度退化.试验与有限元分析得到的柱底截面极限弯矩及最大层间位移角汇总于表3.表中，My，θy分别为理论计算的弹性屈服弯矩及对应的层间位移角；Mp为按理想弹塑性计算的全截面塑性弯矩；Mu为试验得到的试件柱底截面极限弯矩；θu为试验试件达到的最大层间位移角或有限元分析中试件承载力下降到85%时对应的层间位移角；延性系数μ=θu／θy.

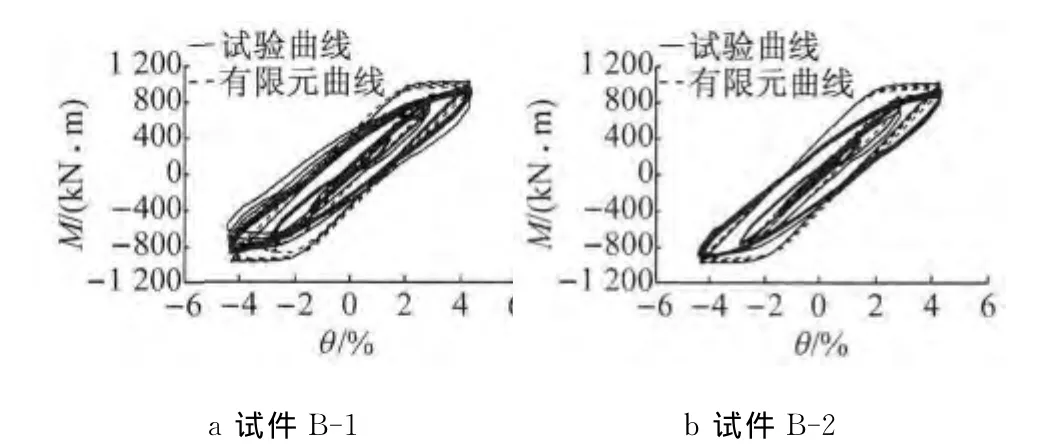
图11 M-θ滞回曲线有限元分析与试验结果对比Fig.11 Comparison of M-θ hysteretic curves of FE analysis and experimental result

根据上述有限元与试验结果的对比可知，ANSYS有限元分析与试验结果吻合较好，能够准确地预测Q690D高强钢焊接箱形截面柱的滞回性能.

为了分析火焰矫正对箱形截面试件滞回性能的影响，以试件B-1为例（试验中两个试件只有火焰校正位置不同），提取试件M-θ骨架曲线进行对比，对比结果如图14所示.可以发现，由于经火焰校正后钢材屈服强度与极限强度均有所降低，导致试件提前进入非线性，极限承载力有所下降，滞回耗能能力下降.

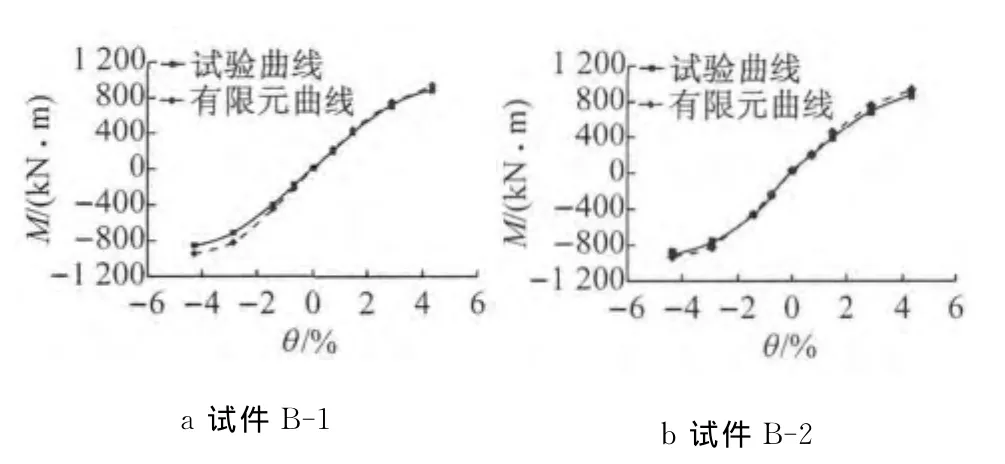
图12 M-θ骨架曲线有限元分析与试验结果对比Fig.12 M-θ skeleton comparison of FE analysis and experimental results

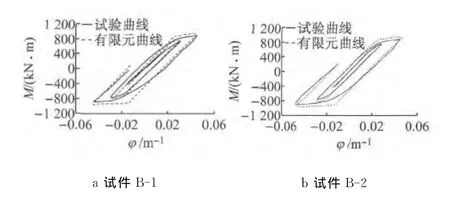
图13 柱底M-φ滞回曲线有限元分析与试验结果对比Fig.13 Comparison of M-φ hysteretic curves of FE analysis and experimental results

表3 试验结果和有限元模拟结果Tab.3 Comparison of experimental and numerical simulation results

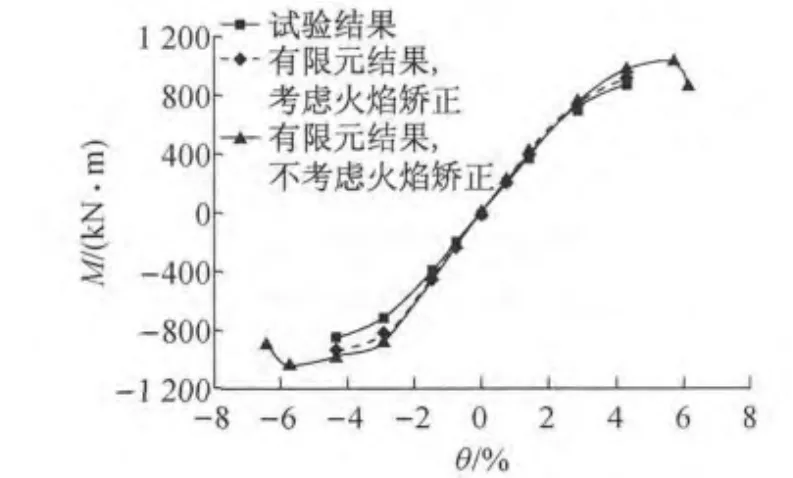
图14 火焰矫正影响Fig.14 Influence of flame correction

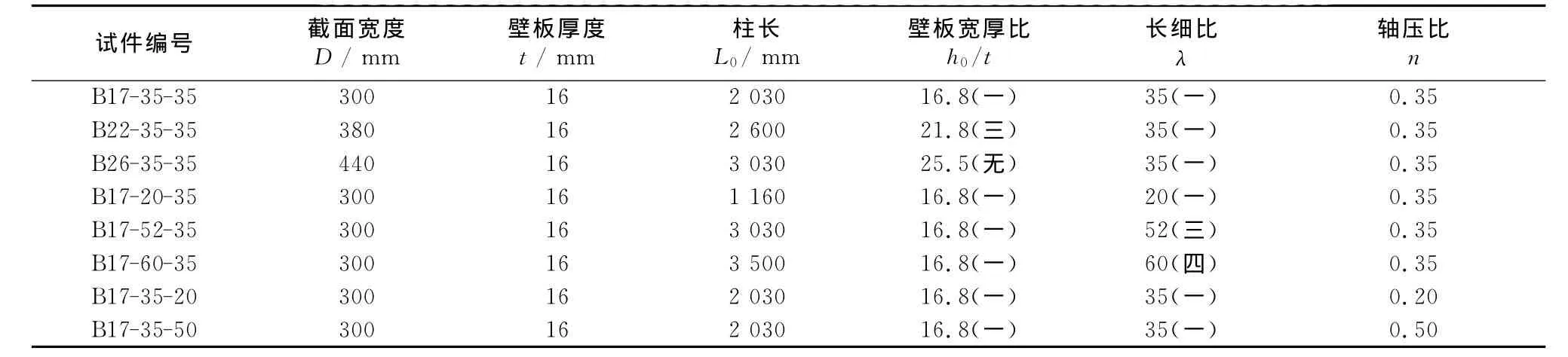
表4 Q690D高强钢焊接箱形截面试件参数Tab.4 Q690DHSS welded box section specimens

4 参数分析

为了进一步研究Q690高强度钢材焊接箱形截面柱的滞回性能，本节利用前面已验证的有限元模型进行参数分析，研究轴压比、构件长细比以及壁板宽厚比等参数对高强钢柱滞回性能的影响.参数分析时，不考虑火焰矫正的影响.

4.1 算例设计

为了研究轴压比、构件长细比及壁板宽厚比对Q690D高强度钢材焊接箱形截面柱滞回性能的影响，设计了8个试件，轴压比分别取0.20，0.35和0.50，构件长细比分别取20，35，52和60，壁板宽厚比分别取16.75，21.75和25.50，具体如表4所示.试件编号为高强钢箱形截面柱、试件壁板宽厚比、构件长细比和轴压比大小的组合.

4.2 结果分析

图15为不同壁板宽厚比下构件弯矩-层间位移角滞回曲线.由图可得不同壁板宽厚比的各试件骨架曲线和正则化滞回耗能指标曲线，见图16，17.正则化滞回耗能指标h为试件M-θ滞回曲线中每一圈滞回环所包含的面积Sh除以弹性应变能

从图15～17可以看出，当构件长细比及轴压比一定时，随着壁板宽厚比增大，构件的变形能力、塑性发展能力和耗能能力有所降低.分析其原因是壁板宽厚比越大，壁板局部失稳发生越早，而且壁板局部失稳发生后试件承载力退化加速.

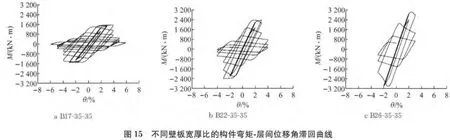
Fig.15 M-θhysteretic curves of specimens with different width-thickness ratios of plate

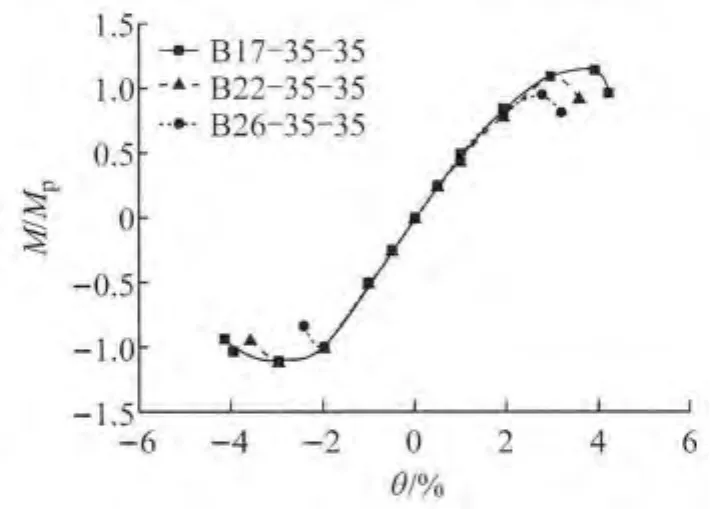
图16 不同壁板宽厚比的试件骨架曲线对比Fig.16 Skeleton curves of specimens with different width-thickness ratios of plate

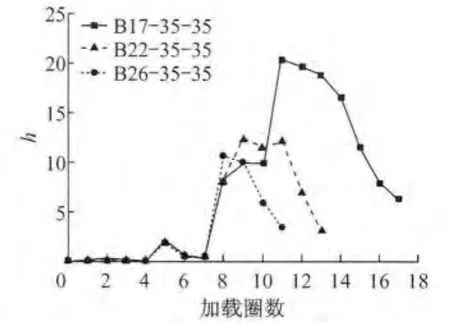
图17 不同壁板宽厚比的试件正则化滞回耗能指标曲线Fig.17 Normalized hysteretic energy curves of specimens with different width-thickness ratios of plate

图18～20为构件长细比的影响.从图中可以看出，当壁板宽厚比及轴压比一定时，随着长细比增大，塑性发展能力和耗能能力有所降低.分析其原因是相同层间位移角下，随着构件长细比增大，二阶效应越加明显，构件塑性发展能力及延性随之减小，但构件最大层间位移角有所增加.

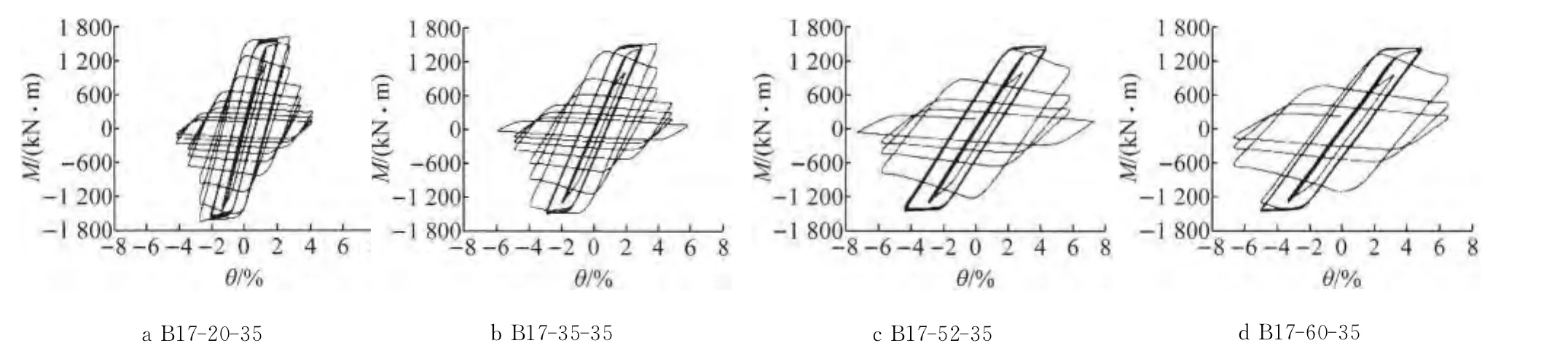
图18 不同构件长细比的构件弯矩-层间位移角滞回曲线Fig.18 M-θhysteretic curves of specimens with different slenderness ratios

图21～23为构件轴压比的影响.从图中可以看出，当壁板宽厚比及构件长细比一定时，随着轴压比增大，构件承载力和耗能能力退化降低，但试件塑性发展能力基本一致.分析其原因是轴压比大的试件，其二阶效应更为明显.

参数分析结果表明，构件的长细比、轴压比或壁板宽厚比增大时，都会导致承载力退化加快，构件塑性发展能力、构件变形能力和耗能能力降低.轴压比增大会使二阶效应更加突出，而壁板宽厚比的增大使局部屈曲提早发生，塑性发展受到限制.各算例的柱底截面极限弯矩及最大层间位移角汇总于表5.

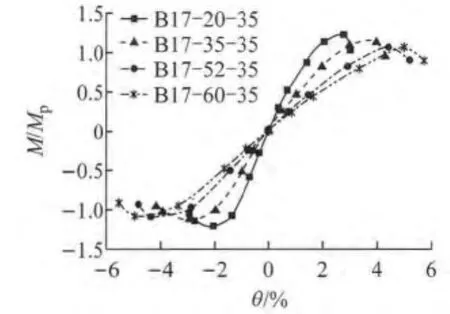
图19 不同构件长细比的试件骨架曲线对比Fig.19 Skeleton curves of specimens with different slenderness ratios

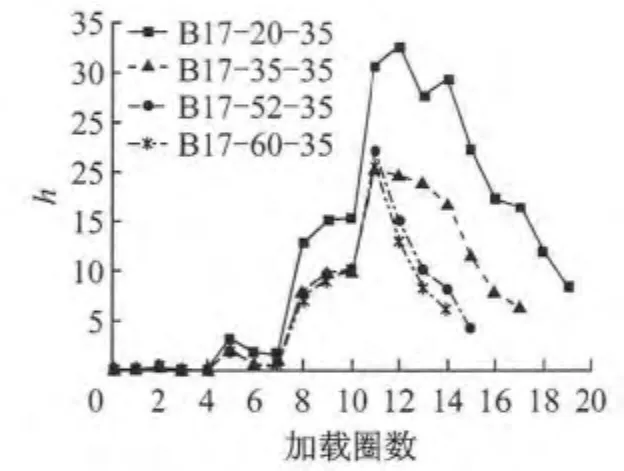
图20 不同构件长细比的试件正则化滞回耗能指标曲线Fig.20 Normalized hysteretic energy curves of specimens with different slenderness ratios

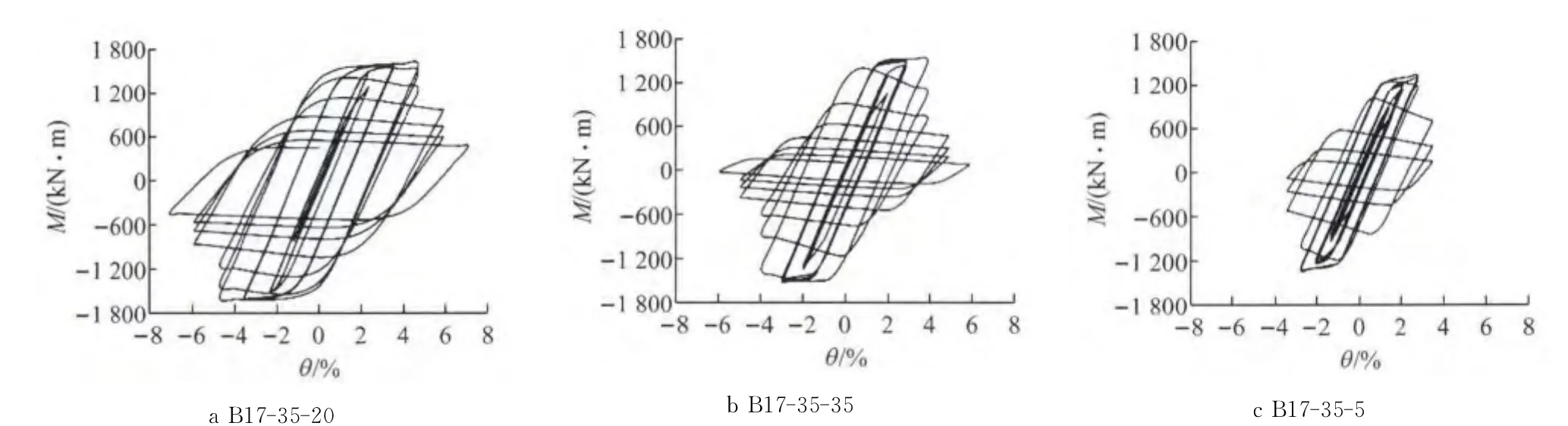
图21 不同构件轴压比的构件弯矩-层间位移角滞回曲线Fig.21 Hysteretic curves of specimens with different axial compression ratios

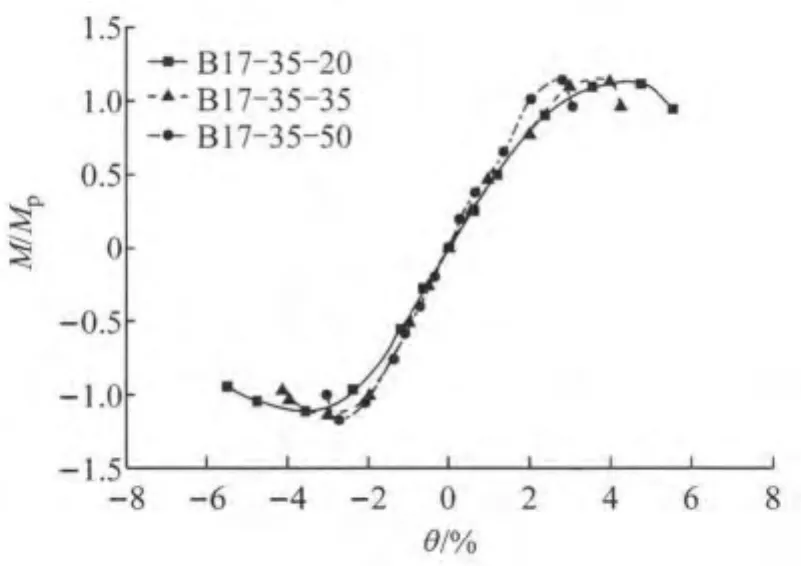
图22 不同轴压比的试件骨架曲线对比Fig.22 Skeleton curves of specimens with different axial compression ratios

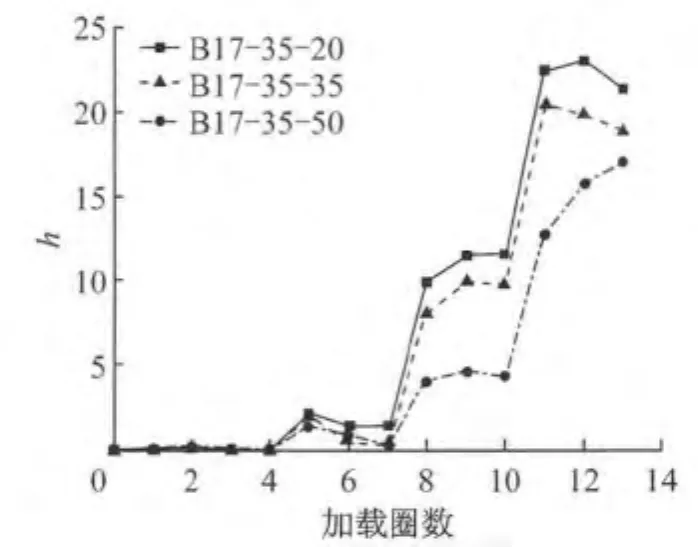
图23 不同轴压比的试件正则化滞回耗能指标曲线Fig.23 Normalized hysteretic energy curves of specimens with different axial compression ratios

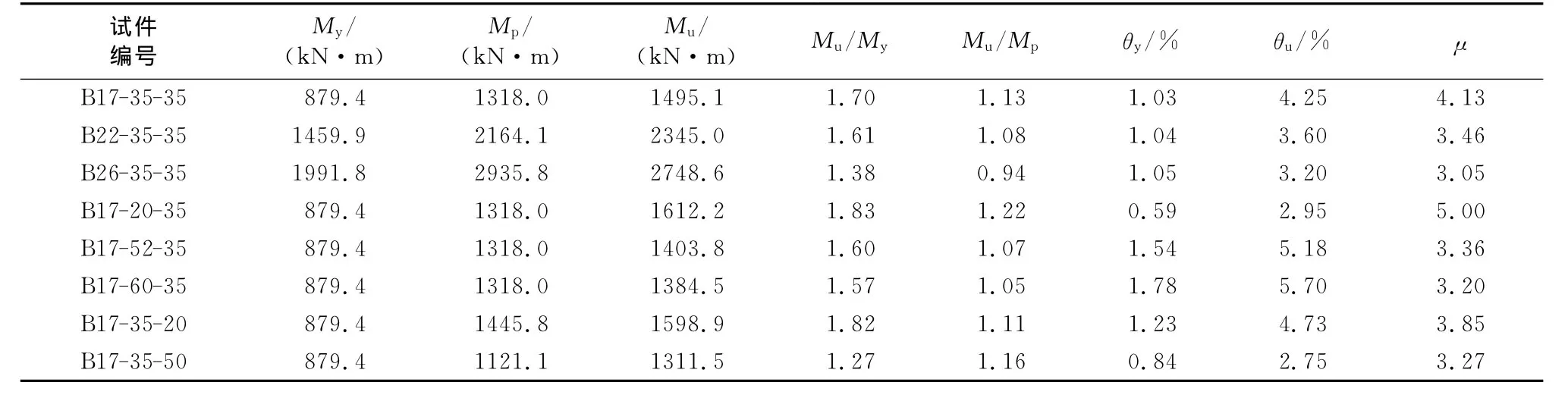
表5 算例结果汇总Tab.5 Summary of results

5 Q690D箱形截面高强钢柱滞回模型

在滞回性能试验研究和有限元参数分析的基础上，提出一个简便、实用而切实可靠的Q690D焊接箱形截面柱的弯矩-曲率滞回模型，如图24所示.其中，My为截面屈服弯矩，φy为截面屈服弯矩对应的曲率.滞回模型的适用范围为满足《抗规》中压弯钢构件长细比、板件宽厚比限值的高强钢焊接柱.图中，直线P1P1′，P2P2′分别经过点（1，1）和点（-1，-1）且斜率均为0.035，直线Q1Q1′，Q2Q2′分别经过点（0，1.6）和点（0，-1.6）且斜率均为-0.2.其变化规则如下：（1）开始加载后，自原点O沿线段①前进，线段①为弹性阶段，其斜率为1；线段①与直线P1P1′交于A点，当超过A点后，进入线段②，其斜率为0.8；（2）如果曲率增量不变号，则沿线段②前进，当到达线段②与直线Q1Q1′交点后，则沿斜率为0.035的直线继续前进；如果沿线段②前进时曲率增量变号，则沿线段③折回，其斜率为1；（3）在线段③中，如果曲率增量变号，即曲线上升，到达B点后沿线段②继续前进，到达线段②与直线Q1Q1′交点后，沿斜率为0.035的直线继续前进；如果曲率增量未变号，即曲线继续下降，经过线段③与直线P2P2′的交点C点后，沿线段④前进，其斜率为0.8；（4）在线段④中，如果曲率增量变号，则曲线折回上升，其斜率为1；如果斜率增量不变号，则继续沿线段④继续前进，经过线段④与直线Q2Q2′的交点D点后，沿线段⑤前进，其斜率为0.035；（5）在线段⑤中，如果曲率增量不变号时，则沿线段⑤前进；如果曲率增量变号，则曲线折回上升，其斜率为1.

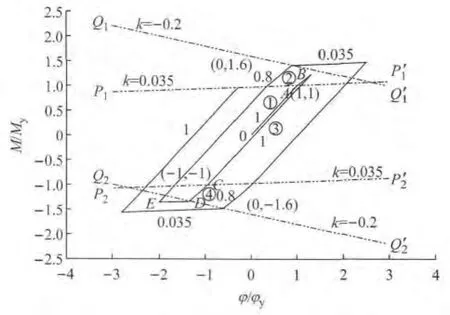
图24 Q690D高强钢箱形截面柱弯矩-曲率滞回模型Fig.24 Moment-curvature hysteretic model of Q690D HSS box section columns

将试验得到的箱形截面试件柱底弯矩-曲率滞回曲线量纲一化后，与滞回模型对比并示于图25.可以看出，试验结果与所建议的滞回规则符合较好.

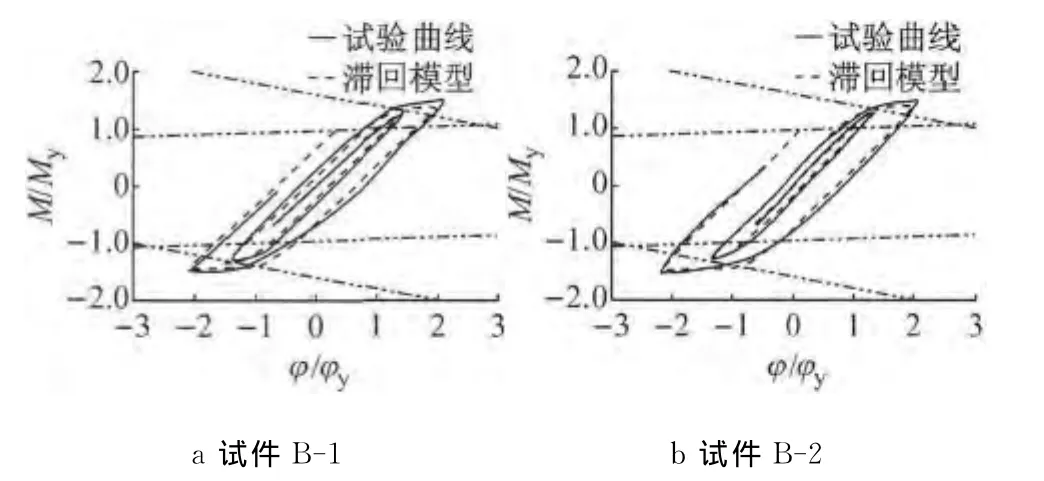
图25 箱形截面试件试验曲线与滞回模型对比Fig.25 Comparison of experimental curve of box section specimens with hysteretic model

6 结论

（1）本文通过对2根Q690D焊接箱形截面柱的低周反复加载试验和有限元模拟，通过分析弯矩-层间位移角滞回曲线和骨架曲线，发现Q690D焊接箱形截面柱的滞回曲线饱满，滞回性能良好，并验证了有限元模型的有效性.

（2）由于火焰矫正的影响，钢材的屈服强度与极限强度都有所降低，使受矫正部位在加载过程中提前进入屈服，并发生局部失稳，导致构件整体刚度下降，提前进入非线性，滞回耗能能力下降.最终试件破坏集中发生在火焰矫正区域.

（3）构件的长细比、轴压比或壁板宽厚比增大时，都会导致承载力退化加快，构件塑性发展能力、构件变形能力和耗能能力降低.轴压比增大会使二阶效应更加突出，而壁板宽厚比的增大使局部屈曲提早发生，塑性发展受到限制.

（4）在试验及有限元分析的基础上，提出箱形截面高强钢柱弯矩-曲率滞回模型，经与试验滞回曲线的比较，验证了滞回模型的正确性.所提模型可用于高强钢焊接柱结构的弹塑性地震反应分析.

［1］ Hans-Peter G，Joel R.Use and application of high-performance steels for steel structures［M］.Zurich Switzerland：IABSE，2005.

［2］ Rasmussen K J R，Hancock G J.Tests of high strength steel columns［J］.Journal of Constructional Steel Research，1995，34（1）：27.

［3］ Rasmussen K J R，Hancock G J.Plate slenderness limits for high strength steel sections ［J］.Journal of Constructional Steel Research，1992，23（1）：73.

［4］ Usami T，Fukumoto Y.Local and overall buckling of welded box columns［J］.Journal of the Structural Division，1982，108（ST3）：525.

［5］ Nishino F，Ueda Y，Tall L.Experimental investigation of the buckling of plates with residual stresses［C］∥Test Methods for Compression Members.Philadelphia：ASTM Special Technical Publication，1967：12-30.

［6］ Beg D，Hladnik L.Slenderness limit of class 3 I cross-sections made of high strength steel［J］.Journal of Constructional Steel Research，1966，38（8）：210.

［7］ 班慧勇，施刚，石永久，等.超高强度钢材焊接截面残余应力分布研究［J］.工程力学，2008，25（增Ⅱ）：57.BAN Huiyong，SHI Gang，SHI Yongjiu，etal.Study on the residual stress distribution of ultra-high strength-steel welded sections［J］.Engineering Mechanics，2008，25（Suppl.Ⅱ）：57.

［8］ WANG Yanbo，LI Guoqiang，CHEN Suwen.Residual stresses in welded flame-cut high strength steel H-sections［J］.Journal of Constructional Steel Research，2012，79：159.

［9］ WANG Yanbo，LI Guoqiang，CHEN Suwen.The assessment of residual stresses in welded high strength steel box sections［J］.Journal of Constructional Steel Research，2012，76：159.

［10］ 李国强，王彦博，陈素文.高强钢焊接箱型柱轴心受压极限承载力试验研究［J］.建筑工程学报，2012，33（3）：8.LI Guoqiang，WANG Yanbo，CHEN Suwen.Experimental study on ultimate bearing capacity of axially compressed high strength steel columns［J］.Journal of Building Structures，2012，33（3）：8.

［11］ 李国强，王彦博，陈素文，等.Q460高强钢焊接箱形柱轴心受压极限承载力参数分析［J］.建筑结构学报，2011，32（11）：149.LI Guoqiang，WANG Yanbo，CHEN Suwen，etal.Parametric analysis of ultimate bearing capacity of Q460 high strength steel welded box columns under axial compression［J］.Journal of Building Structures，2011，32（11）：149.

［12］ 李国强，闫晓雷，陈素文.Q460高强钢焊接箱形压弯构件极限承载力试验研究［J］.土木工程学报，2012，45（8）：67.LI Guoqiang，YAN Xiaolei，CHEN Suwen.Experimental study on the ultimate bearing capacity of welded box-section columns using Q460 high strength steel in bending and axial compression［J］.China Civil Engineering Journal，2012，45（8）：67.

［13］ 闫晓雷，李国强，陈素文.Q460高强钢焊接箱形压弯构件极限承载力数值分析［J］.建筑钢结构进展，2013，15（3）：12.YAN Xiaolei，LI Guoqiang，CHEN Suwen.Numerical analysis of ultimate bearing capacity of welded box-section columns Q460 high strength steel in bending and axial compression［J］.Progress in Steel Building Structures，2013，15（3）：12.

［14］ Usami T，Fukumoto Y.Welded box compression members［J］.Journal of Structural Engineering，1984，110（10）：2457.

［15］ CHEN Yiyi，WU Qi，ZHOU Feng，etal.Experiments on Q460 high-strength steel beam-columns and the application［C］∥The 6th International Symposium on Steel Structures（ISSS-2011）.Seoul：Korean Society of Steel Construction，2011：964-969.

［16］ 施刚，邓椿森，班慧勇，等.Q460高强度钢材工形压弯构件抗震性能的试验研究［J］.土木工程学报，2012，45（9）：53.SHI Gang，DENG Chunsen，BAN Huiyong，etal.Experimental study on the seismic behavior of Q460 high strength steel I-columns［J］.China Civil Engineering Journal，2012，45（9）：53.

［17］ 李国强，王彦博，陈素文，等.Q460C高强度结构钢焊接H形和箱形截面柱低周反复加载试验研究［J］.建筑结构学报，2013，34（3）：80.LI Guoqiang， WANG Yanbo， CHEN Suwen，etal.Experimental study of Q460C high strength steel welded H-section and box-section columns under cyclic loading［J］.Journal of Building Structures，2013，34（3）：80.

［18］ 李国强，王彦博，陈素文，等.Q460C高强度钢柱滞回性能有限元分析［J］.建筑结构学报，2013，34（3）：87.LI Guoqiang，WANG Yanbo，CHEN Suwen，etal.Finite element analysis on hysteretic behavior of Q460C high strength steel box-section and H-section columns［J］.Journal of Building Structures，2013，34（3）：87.

［19］ 中华人民共和国住房和城乡建设部.GB50011-2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.Ministry of Housing and Urban-Rural Development of the People's Republic of China.GB 50011-2010 Code for seismic design of building［S］.Beijing：China Architecture &Building Press，2010.

［20］ 中国建筑科学研究院.JGJ 101-96建筑抗震试验方法规程［S］.北京：中国建筑工业出版社，1997.China Academy of Building Research.JGJ 101-96 Specificating of testing methods for earthquake resistant building［S］.Beijing：China Architecture &Building Press，1997.

［21］ 孙旭.Q690钢材料力学特性研究［D］.上海：同济大学，2013.SUN Xu.Research on mechanical properties of Q690［D］.Shanghai：Tongji Unviersity，2013.