基于SPSS软件的初中数学试卷定量分析研究

杨雪峰

[摘 要] 本文通过实例介绍了在大数据时代背景下，如何运用SPSS统计软件对试卷质量，以期帮助教师科学分析测验试卷，进而根据测验情况反馈及时改进教学工作，并从测验中筛选出优秀试题，建立试题库，为实施标准化考试服务.

[关键词] SPSS；质量分析；成绩分析.考试是教育评价的重要手段之一，而试卷质量分析正是考试评价的重要组成部分，选择科学的分析方法是有效分析试卷质量的关键.本文以笔者所在学校初一年级2013—2014学年第二学期数学期末考试试卷为例，利用SPSS 19.0软件对试卷质量进行了定量分析和检验，目的是帮助广大同行教师能够运用SPSS软件对试卷进行定量分析，以期提高教师分析试卷、命制试卷的能力.

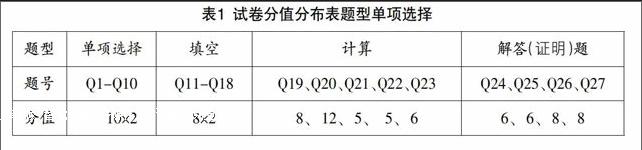
试卷定量分析主要包括试卷质量分析和试卷成绩分析两部分. 根据教育评价理论，试卷分析的指标有：难度、区分度、信度、效度等.成绩分析指标主要有参加考试的人数、最高分、最低分、平均值、标准差以及等级分布、班级间的差异性检验等. 本文从笔者所在学校初一年级2013—2014学年第二学期数学期末考试试卷中随机抽取100份试卷进行试卷质量的定量分析，试卷分值分布情况见表1.

1. 定义变量

用鼠标单击数据编辑器下方的“变量视图”标签，进入变量命名定义界面.在“名称”标题下依次定义题号Q1—Q27，总分定义为Total. 在“标签”标题下注明对应各行定义的内容：第1题—第27题以及总分.其中题号和总成绩均定义成“数值”类型，“小数”（小数点后长度）为0，其余各项均使用默认.

2. 输入数据

数据文件的建立可用以下2种方法：第一，对于Excel，oxpro，Access等文件，采用SPSS软件直接调入的方法；第二，用SPSS提供的数据编辑窗口直接输入数据，这两种方法是最为简单易行的方式. 采用第二种方式时，返回数据编辑器界面，从第一行第一列起直接输入题目成绩，依次每行输入一个学生的成绩，每列输入一个题目的成绩，最后一列输入每名学生的总成绩.

1. 建立样本分数段分布直方图

根据录入的数据表，运行菜单：“分析→描述统计→频率”，得到频数表，然后得到复选框，导入要建立频数分布表和直方图的项目（即总分），同时运行菜单：“分析→描述统计→频率→图表→直方图”，勾选“在直方图上显示正态曲线”，即可得到分数段分布直方图. 通过学生成绩分布直方图和频数分布表可以看出，这100名学生的成绩接近正态分布，平均分为74.75分，最高分100分，最低分8分，极差达到92分，标准偏差为20.682，标准差比较大，说明学生个体间存在较大的差异，不及格的人数占20%，60—80分之间的人数占27%，85分以上高分段人数较多. 说明除个别学生外，大部分学生答题情况较好.

2. 难度分析

难度（Difficulty）是指试题的难易程度. 对于客观性试题（通常指选择题），其难度计算公式为P=，式中P为难度指标值，R为答对某题的人数，N为考生人数. 对于主观性试题，其难度计算公式为P=，式中为学生在该题得分的平均值，W为该题的满分值. 通过难度的定义可以看出：P值越大，说明题目越简单；P值越小，说明题目越难. 一般认为，难度适中更能客观反映出学生的学习效果情况，多数试题难度分布在0.3—0.7之间，选拔性测试P=0.5左右为宜，通常期末考试为目标参照性考试，P可适当偏高，全卷平均难度以0.7左右为宜，0.6—0.8为正常.

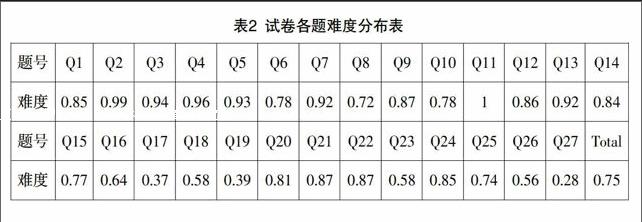
使用SPSS进行难度分析的具体操作方法为：运行菜单“分析→描述统计→描述”，将全部字段选入变量中，单击“确定”按钮，可得到各题的均值和极值，然后建立一个包含均值和各题满分值的数据文件，单击“转换→计算变量”，出现“计算变量”对话框，在“目标变量”中输入要计算的难度系数P，在“数字表达式”中输入公式“均值/满分”，得到各题的难度系数.本次考试的难度统计结果如表2所示.

通过表2可见，试卷整体难度为0.75，适合期末考试难度目标，难易适中，大部分题目难易程度尚可，其中第2、3、4、5、7、11、13题偏易，可适当增加难度，但由于期末考试属于目标参照性考试，不是选拔性考试，第27题难度稍大，对初一学生来说可适当增加解题梯度提示.从题型来看，难度分配合适，试卷编排较合理.

3. 区分度分析

区分度（Discrimination）是指测验题目对学业水平不同的学生的区分程度或鉴别能力. 具有良好区分度的测验，实际水平高的被试应得高分，水平低的被试应得低分. 它是测验是否有效的“指示器”，被作为评价试题质量，筛选试题的主要指标与依据.

试题区分度的计算方法很多，在此介绍一种比较方便的方法. 对于客观题，使用等级相关分析，使用斯皮尔曼（Spearman）等级相关分析；对于主观题，看成是非等距间距测度的连续变量，并且样本数大于30，采用皮尔逊（Pearson）相关分析来对试题进行分析，即求总分与每个试题得分间的积差相关系数作为试题的区分度. 一般地，区分度D≥0.4表示区分度很好；0.3≤D<0.4表示区分度良好，如能改进更好；0.2≤D<0.3表示尚可，需改进；D<0.2表示区分度差，需淘汰.

在本文使用的样本中，第1～10题为客观题；第11～27题为主观题. 具体的分析方法：运行菜单“分析→相关→双变量”，在弹出的“双变量相关”对话框中选择各个客观题字段和总分进入“变量”，然后在“相关系数”中勾选“Spearman”，完成后即可得到客观题的区分度. 主观题的区分度方法同上，区别在于在“相关系数”中勾选“Pearson”即可. 通过各题的区分度可以看出，第2题的区分度不够，样本中得分率为100%，需要淘汰，第4、7题的区分度分别为0.268和0.217，区分度尚可，但需改进. 从题型来看，主观题的区分度明显高于客观题.同时结合各题的难度可以看出，并不是难度越高，区分度就越好，譬如第20题难度系数为0.81，题目偏简单，但它的区分度达到了0.789，区分度很好，第26题难度系数是0.56，难度并不是最高，而区分度达到了0.808，是整卷区分度最高的，而试卷最后的压轴题即第27题，难度系数为0.28，属于难度最大的题，但它的区分度是0.608，这充分说明平时我们教师在命制试卷时，认为难题具有较好的区分度是不科学的，不能一味追求难题甚至怪题、偏题，而应在大纲要求内，科学合理灵活地考查学生对知识的掌握.

4. 信度分析

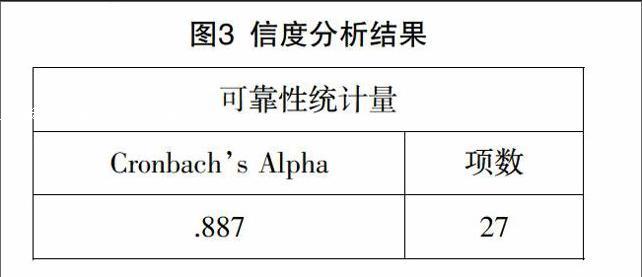
信度（Reliability）r是反映试卷题目得分一致性程度的统计量，表示考试的可靠性，取值范围为0～1，其值越大，信度越高. 一般认为r在0.9以上可靠性较好.在试卷信度的检验中一般采用的是同质性信度. 具体的分析方法：运行菜单“分析→度量→可靠性分析”，打开信度分析对话框，在弹出的对话框中将所有表示题目的字段全部选择进入“项目”框中，在“模型”栏后的下拉列表采用默认的Alpha方法，得到分析结果如表3所示. 从分析结果可以看出，本次考试的信度系数为0.887，信度较高，在教师自编的试卷中，试题的信度系数一般应要求在0.85以上，而标准化考试应在0.9以上.本文所研究的试卷信度为0.887，结果说明本次考试的信度较好.而为了提高试卷的信度，可以从以下几方面改进：适当增加试题的数量、保持所有试题的难度接近正态分布、努力提高试题的区分度、严格监考和按评分标准给分.

试卷分析表的生成

经过以上分析得到各项指标的值和图形，使用复制、粘贴功能将它们粘贴到Word文档相对应报表栏目中，合成试卷分析报告. 试卷分析包括定量分析和定性分析，本文主要涉及的是试卷的定量分析.

考试是一种测量，试卷就是测量工具，用科学的测量理论对组成试卷的每一道题进行定量分析，取优弃劣，为本课程教学积累资料，将进行分析后的试题进行分类入库，可以降低出现类似本次考试个别试题选题不科学的概率，防止出题的随意性，能够促进考试的科学化与标准化，进而有效地测出被测对象的真实水平. SPSS在教学评价中有着极为广泛的应用，除了可以对不同科目的成绩的相关性进行分析之外，还可对评价效度进行测量，以及对多个平行班级的成绩进行差异性检验. 充分利用SPSS的各种统计功能将有助提升我们教学研究的分析水平，进而使我们的教学方式有所改进，整体教学效果质量有所提升.