基于 Stateflow的地下铀矿山运提系统可靠性仿真研究

陈 刚，孔凡峰，戴剑勇

(1.南华大学，湖南衡阳421001;2.中核北方铀业有限公司，辽宁兴城125100)

基于 Stateflow的地下铀矿山运提系统可靠性仿真研究

陈 刚1，孔凡峰2，戴剑勇1

(1.南华大学，湖南衡阳421001;2.中核北方铀业有限公司，辽宁兴城125100)

运输与提升系统是地下铀矿山生产大系统中的重要子系统，研究运提系统可靠性对合理安排维修周期、节省企业成本、提高产量具有重要意义。针对传统可靠性方法在复杂可修系统可靠性分析中的局限，提出了基于Stateflow的运提系统可靠性仿真方法。为了更加符合实际，模型中将运提系统作为柔性系统处理，并认为维修资源有限。最后用模型对一实例进行分析，仿真结果表明，基于Stateflow的仿真分析方法能够有效评估运提系统的可靠性参数。

运输提升系统;Stateflow;可靠性

随着世界能源格局的转变，铀矿的需求增大，这促使铀矿山的开采量越来越多，进而导致井下设备的大型化和复杂化。如何能使一个复杂的地下开采系统可靠高效的运行成为人们迫切需要解决的问题。同时，现代系统工程理论的成熟，使得可靠性能够作为重要的一员与性能、成本、时间等技术经济指标一起，成为评价系统优劣的主要指标。可见提高和改善系统可靠性，对系统可靠性进行分析研究是我们面临的又一项紧迫性任务。铀矿山地下开采中，在其他生产工艺正常运行的情况下，运输系统与提升系统可靠与否是运提系统利用率发挥的关键，其可靠性的高低直接影响到矿井地下生产工艺的安全稳定、经济效益以及产量［1－4］。因此，对运提系统可靠性进行分析和研究有重要的意义。

目前，主要是利用下面三种方法对其进行分析:图形演绎法(基于可靠性框图和故障树)、数学解析法(基于概率论和马尔可夫链)、仿真法(基于事件和时间)［5］。研究人员普遍认为复杂可修系统可靠性仿真主要存在以下问题:由于系统结构复杂多样且子系统失效和修复分布任意，因此造成建模与仿真比较困难。此外，笔者通过查阅大量文献发现:大多数研究人员在做地下矿山运输与提升系统可靠性仿真时假设系统为刚性串联系统，只要有一个子系统出现故障，运提系统就得按故障处理。现实情况则不然，如溜井可以作为一个临时的储矿仓，上阶段矿车出故障后短时间内不会影响到后续运输系统，此时的系统不能按故障处理;还有维修资源通常是有限的，甚至有时是不足的，这就需要按照一定规则安排修理任务。针对上述面临的问题，本文利用状态机理论和排队理论来反映运提系统在现实中的情况。

矿井运提系统是一个多设备、多工艺、多环节，受井下开采环境影响的复杂系统，并且由于井下作业地点的复杂性、交叉性，图形演绎法和数学解析法很难对系统做出符合实际的可靠性分析，甚至有时候连得出系统的可靠性数学表达式都不太可能。相对于以上两种方法，仿真法以其结构灵活简单、编程容易实现而成为了大型复杂系统可靠性分析的有力工具。因此，本文提出一种基于Stateflow的运提系统可靠性仿真方法，可以准确预计运提系统的可靠度、维修度等一系列可靠性指标，从而为促进运提系统的合理使用及维修和更新决策提供理论依据［6－7］。

1 基于Stateflow的运提系统可靠性仿真模型

1.1 Stateflow工具箱

Stateflow是一个可以与Simulink工具箱在仿真中完美兼容的软件包。它是一种图形化的建模和仿真环境。Stateflow采用面向对象的编程思想，即属性、事件和方法。一个Stateflow图由图形对象和非图形对象构成，如图1所示。非图形对象则包括数据(Data)、事件(Event)和目标(Target)对象。

图1 Stateflow中的图形对象Fig.1 The graphics objects in the Stateflow

状态(Chart)在Stateflow框图中用圆角矩形来表示，状态中的所有属性均由矩形左上角的标签来表示。状态的标签一般可以由三个部分组成: Name、Comments和State Action。状态之间的转换用带有箭头的曲线来连接，箭头的方向即表示状态转移的方向。状态转移时的条件、动作等都直接标注在线段附件，具体格式如下:

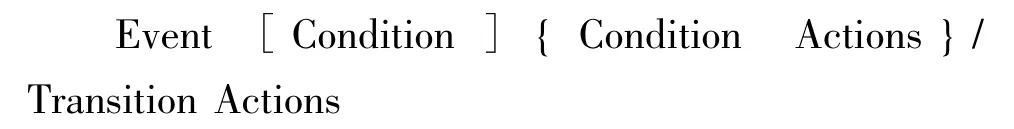
上面表示的分别是事件、条件、条件动作、转移动作，它们不一定每次都要完整地出现，但书写内容一定要按照上面的格式来写。

1.2 运提系统可靠性Stateflow仿真模型构建

利用有限状态机面向对象的思想将运提系统这一复杂系统及其内部子系统用Stateflow状态图来表示，通过为代表运提系统的 Stateflow状态图添加State、Data、Event、Action描述各个系统之间的运行及其与其它系统的交互，最后通过定义的仿真时钟来推进驱动整个仿真模型的运行，并记录仿真的时间，从而得到该运提系统的可用度、MTBF、MBTR等可靠性参数的统计值。具体步骤如下:

1)确定运提系统中的实体

Stateflow的模型构造是面向对象的。所以首先需要确定系统中的实体，运提系统中的实体比较简单也比较固定，即各项作业的设备子系统。各设备子系统、维修子系统都属于总系统，为了能够清晰地表示这些子系统互相间的关系，在具体建模中可以将代表各个子系统的框图放置到代表总系统的框图中，也可以将它们并列放置在一起。这里采取前一种方式，也就是将各个子系统置于虚拟的总系统中。子系统和中系统都会随着仿真时钟的推进发生变化，所以它们是并行关系。在Stateflow中，虽然并行状态在理论上是同时发生，但实际仿真中各个状态的执行仍然具有先后顺序，这就需要通过实际中系统的发生顺序来确定模型实体的相互关系，以确定其符合实际的执行顺序。

系统中的实体即为生产工艺中的设备，由它模拟设备来不断地产生故障推动整个复杂系统的运行。如图2所示，前六个状态框图分别表示溜井(Orepass)、振动放矿机(Vibro－droper)、矿车(Tramcar)、电机车(Barney)、操车系统(Operation control)、提升机(Elevator)。Repair状态即为维修系统，System状态是为处理系统仿真数据而创建的，各状态为并行关系(状态图边框为虚线)。对于维修系统，当没有实体故障时其为空闲，当出现实体故障时其处于激活状态，并向总系统汇报激活次数以便统计维修次数;维修系统中还存在排队现象，当同一时间有多个设备故障时，维修系统按照“先到先维修”的策略进行维修。仿真时按照图1～5顺序执行。

图2 仿真系统总框图Fig.2 The block diagram of simulation system

2)确定实体添加的数据

数据是模型仿真的基础，因此需要添加相应的输入、输出数据和内部数据(设备属性)。对于整个仿真系统来说，它的外部数据就是用来模拟时钟推进的脉冲信号生成模块，内部数据是各种设备(提升机、电机车等)持续工作的时间分布参数，输出数据是每次仿真完成后系统正常工作的时间。

图3 维修系统中提升机(R6)维修框图Fig.3 The maintenance diagram of elevator(R6)in maintenance system

由于各种设备的MTBF服从不同的概率分布，如指数分布、正态分布、威布尔分布等。所以每个实体都有自己独自的随机数发生器。对于这些分布，Matlab都有相应的随机数生成函数，如normrnd可以生成正态分布随机数，betarnd生成β分布随机数。所以，我们在Stateflow仿真中可以很方便地生成服从任何概率分布的随机数。如图3中，维修子系统R1模块中的Repair状态下“y=ceil(－80*log (ml.rand()))”y的值是服从指数分布的随机数，在此表示提升机(R6)的维修时间服从指数分布(本文为简化仿真难度，假设统计到的提升机维修时间服从负指数分布，这种假设是符合实际的)。其它的内部数据以及子系统的数据在这里不再赘述，可以参见实例。

3)确定触发状态的事件

整个Stateflow的运转需要事件来驱动。对于整个Stateflow状态图来说，其又需要一个事件来模拟时钟，所以这里需要一个输入事件 timer;对于各个设备子系统，需要向Repair状态和System状态发送相应的故障事件FAULT1～FAULT6;对于Repair状态，当其对子系统维修完毕之后，要向相应的子系统发送维修成功事件GOOD1～GOOD6，而System状态接受各子系统与Repair状态发送的事件。如图4，为电机车(Barney)状态图内部结构图，其中“timer”、“FAULT3”、“GOOD3”为电机车在仿真中所对应的事件。

4)添加维修框图(Repair)

rank(s)函数将设备编号s加入数组F，同时向System发送FAULT事件;而dequeue()函数则是将维修好的设备从数组F中删除，同时分别向相应修理好的设备Ei与System发送GOODi(i=1，2，3，4，5)与GOOD事件;这两个函数共同作用，实现了维修系统“先到先维修”的排队准则。具体如图5、6所示。

5)添加统计框图(System)

所有设备状态图和维修状态图构建完成后，添加统计框图System，如图7所示，主要负责控制时钟与统计仿真结果数据。

图4 电机车状态框图Fig.4 The state diagram of barney

图5 Repair框图Fig.5 The diagram of repair

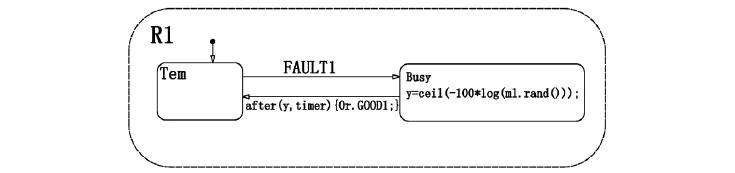
图6 振动放矿机(R1)维修框图Fig.6 The maintenance diagram of vibro－droper(R1)

当仿真开始时，首先进入默认状态On，时钟开始计时。随着仿真的推进，统计框图会不断地接收到设备故障的信号，将这些信号综合后通过真值表(truth table)判断系统何时故障，如果故障就会触发“condition==0”这一动作，从而使状态由On转移到Off，同时时钟停止计时。当故障设备全部维修完好系统可以正常工作时，就会触发“condition==1”这一动作，则状态由Off转移到On，仿真时钟继续计时。在仿真中统计得到的数据直接保存到Workspace中，以备后续Simulink仿真调用。

通过完成上述五个步骤后，再向Simulink模型中添加相应辅助模块就可以进行仿真了。

2 仿真实例分析

图8为简化后的北方某地下铀矿山运输与提升系统中部分设备的可靠性逻辑框图。

本文以此系统作为实例进行仿真。根据该矿某一回采中段现场统计得出的各设备故障与维修分布函数类型及参数见表1。

2.1 建立Simulink仿真模型

在Simulink仿真平台中设置相应辅助模块，如图9所示，构成完整的系统仿真框图。其中Pulse Generator(脉冲信号发生器)产生单位周期的脉冲信号来触发时钟事件timer;Display(显示数据模块)显示每次仿真的再次出动准备时间T。设备可靠性仿真数据通过GUI界面的属性设置栏进行输入，为了体现不同设备在仿真运行中的差异性和整个运提系统的复杂性，每个设备可以指定其可靠性分布函数的类型。设置好各模块的参数后就可以进行仿真了。

图7 统计框图SystemFig.7 System of statistical diagram

图8 简化后的某地下铀矿山运提系统部分设备可靠性框图Fig.8 Reliability diagram of some devices in a uranium mine transportation and winding system after simplified

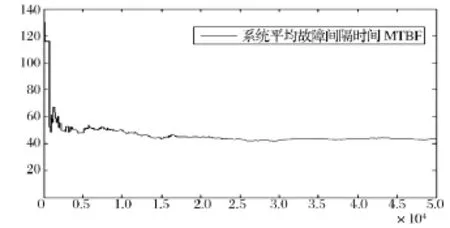
图9 运提系统可靠性仿真模型图Fig.9 The simulation model diagram of reliability in transportation and elevation system

表1 各运提设备故障与维修时间分布类型及参数Table 1 Distribution patterns and parameters of MTBF and MTBR in transportation and elevation equipment

2.2 仿真试验

以图8所示的可靠性模型为例，假设6个设备均为可修复的，故障分布及维修分布参数如表1所示，故障率分别为 λ1、λ2、λ3、λ4、λ5、λ6。按照解析法，根据可靠性理论中并联与串联的计算公式，该可靠性模型的平均故障间隔时间(MTBFS)见式(1)。

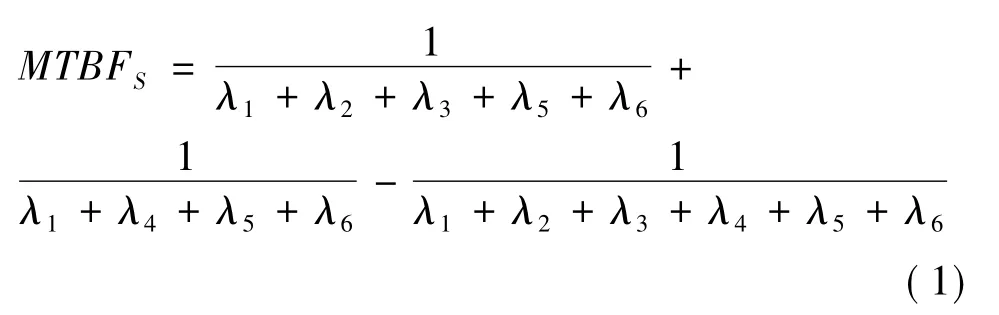
将表1中的故障率数字带入式(1)，最终可求得系统的平均故障间隔时间为42.847。

将基本可靠性参数输入到系统中，然后进行仿真，在运行了5万个仿真时钟后，最终产生的系统平均故障间隔时间以及与解析解的误差百分比如图10、11所示。仿真结束后，最终得出的MTBFS大约为41.287个仿真时钟，经反复仿真后可知，当系统仿真运行大于4万个仿真时钟时，最后得出的结果与解析解的误差百分比基本维持在1%以内，完全可以满足实际工程的需求［8］。由分析仿真得出的系统可靠性数据，我们可以得出系统在运行过程中的稳定性，从而为系统的改进及维护提供可供参考的数据。

图10 仿真运行结果Fig.10 The result of simulation

图11 仿真结果误差分析Fig.11 The error analysis of the simulation results

3 仿真结果分析

本论文设计了基于Stateflow的运提系统可靠性仿真模型，并利用某地下铀矿山运提系统可靠性模型进行了仿真，其结果表明仿真得出的数据与解析解的误差百分比基本维持在1%左右，符合实际工程中误差范围要求，说明本文设计的模型在系统可靠性仿真中是有效的。用Stateflow来对复杂系统进行仿真的优点是其他程序语言不能比拟的，它使用一种简单易懂的图形语言将建模与编程过程结合在一起，且能与Simulink完美结合，能够有效地评估系统在运行中的可靠性，具有很强的实用性。

［1］张光剑.地下矿山提升运输系统可靠性及影响因素研究［D］.昆明:昆明理工大学，2008.

［2］吕学志，于永利，刘长江.基于Stateflow的复杂可修系统的建模与仿真方法［J］.指挥控制与仿真，2009，31(6):71－75.

［3］刘丰志，李仲学，李翠平，等.基于Agent的金属矿地下开采工艺动态仿真系统［J］.金属矿山，2012(3):110－114.

［4］Zuliani P，Platzer A，Clarke E M.Bayesian statistical model checking with application to Stateflow/Simulink verification［J］.Formal Methods in System Design，2013，43(2):338－367.

［5］REN Fan，YU Yongli，LV Xuezhi.Simulation Research for E-quipment System Availability Based on Stateflow［C］//2010 International Conference on Management Science and Engineering (MSE 2010):61－64.

［6］任帆，于永利，吕学志.基于Stateflow的设备维修过程仿真研究［J］.计算机工程与应用，2011，47(21):217－219.

［7］张威.Stateflow逻辑系统建模［M］.西安:西安电子科技大学出版社，2007:25－52.

［8］韩可琦，才庆祥，卢明银.矿业系统可靠性［M］.徐州:中国矿业大学出版社，2002:98－100.

Simulation study for reliability in uranium mine transportation and elevation system based on Stateflow

CHEN Gang1，KONG Fanfeng2，DAI Jianyong1
(1.University of South China，Hengyang Hunan 421001，China; 2.North Uranium Co.，Ltd.，CNNC，Xingcheng Liaoning 125100，China)

Transportation and elevation system is a very important subsystem in the uranium mine production system.Therefore，it is important to study its reliability for arranging maintenance cycle，saving enterprise costs and raising production.In order to overcome the limitation of traditional reliability method，this paper presented a simulation method for reliability in uranium mine transportation and elevation system which is based on Stateflow.To accord with actual，the transportation and elevation system was taken as flexible system，and the maintenance resource is thought to be limited.Based on it，a case is studied using the simulation model.The results show that the simulation method can efficiently evaluate parameters of reliability in transportation and elevation system.

transportation and elevation system;stateflow;reliability

TD53

Α

1671-4172(2015)01-0095-06

国家自然科学基金(51174116);湖南省自然科学基金(10JJ2041)

陈刚(1989－)，男，硕士研究生，采矿工程专业，主要从事安全系统工程方面的研究。

10.3969/j.issn.1671-4172.2015.01.022