变电站主接线方式可靠性评估与方案优选

徐小宁

变电站主接线方式可靠性评估与方案优选

徐小宁

（浙江广厦建设职业技术学院 东阳 322100）

针对传统可靠性评估方法在变电站主接线可靠性评估中的局限性，用贝叶斯网络法对变电站主接线进行可靠性评估且对其方案优选。为此，选取两种目前常用的主接线方式作为应用实例，首先针对系统进行功能和结构分解，获得系统各功能模块的逻辑关系图，然后确定从发电机到负荷端的最小路径，并以此为过渡建立以各功能模块为节点的贝叶斯网络，在此基础上计算出两种主接线方式的系统可用度，并找到两种主接线方式在可靠性方面的薄弱环节。计算结果表明，贝叶斯网络法既能帮助工程人员选择变电站主接线方式，还可指导今后变电站的维修工作，具有较大实际意义。

变电站 电气主接线 可靠性评估 方案优选 贝叶斯网络

1 引言

变电站是电网中至关重要的节点，承担着电力系统中电能汇集和分配功能，其运行的经济性与可靠性直接关联电网的性能[1-3]。电力系统安全、可靠运行是电网设计的基本要求，变电站中电气主接线可靠性往往直接影响变电站工作的可靠性，从而影响电网的可靠性[4]。因此，变电站电气主接线方案的优选一直是研究的热点。

变电站常用的主接线方式有多种，由于变电站在电网中的重要地位，常需尽可能选用可靠性较高的电气主接线。因此，变电站的可靠性评估成为变电站设计阶段的首要任务，且是方案优选的重要依据。故障树分析（FTA）法和贝叶斯网络（Bayesian Networks）法是系统可靠性评估的两种常用方法[5-7]。应用贝叶斯网络法分析复杂系统的可靠性时，需要先找到它的最小路集，并以此作为过渡建立贝叶斯网络[7]。贝叶斯网络法有其独特的优点，表现在不仅可以在已知元件状态的情况下准确评估系统可靠性，还可以查找系统中哪些元件对系统可靠性影响最大，即可以定量给出某个元件或几个元件在系统可靠性中占的比重。目前还没有学者提出将贝叶斯网络法应用于变电站主接线方案优选，即未能解决查找变电站主接线中哪个电气元件对系统故障的影响概率较大问题。

2 贝叶斯网络法概述

贝叶斯网络是Pearl在总结前人工作的基础上提出的，其结合了人工智能，概率理论，图论，决策分析等相关内容，是目前不确定知识表达和推理理论有效的理论模型之一，可以从不完全，不精确和不确定的信息中作出推理[8-10]。贝叶斯网络能很好的表示变量的随机不确定性和相关性，并能进行不确定性推理，因此，将贝叶斯网络法应用于电力系统可靠性评估，能较好的弥补传统可靠性评估的不足[11,12]。一个简单的贝叶斯网络如图1所示。

图1 简单贝叶斯网络

图1中任何一个“黑点”表示一个节点，节点可以是任何问题的抽象，如开关状态，小开关元件，子系统等。箭头表示节点之间的联系，由父节点指向子节点，是信息传递的方向。a，b，c节点没有父节点，称为根节点。根节点代表最初的信息，是贝叶斯网络计算的基础。s节点没有子节点，称为叶节点[13]，常代表贝叶斯网络求解的最终变量。除根节点外，节点分为“与”节点类型与“或”节点类型。串联系统中各子系统为“与”节点关系，并联系统的子系统中各子系统为“或”节点关系。

根据节点的类型及根节点的信息，可以逐级递推出叶节点的信息。由于贝叶斯网络双向推理的特点，也可以假设叶节点的信息对根节点信息进行判断，该过程用到贝叶斯概率公式，即

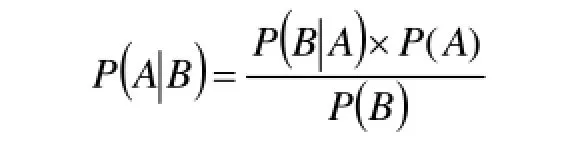
贝叶斯网络双向推理计算分为精确和近似两类算法。前者方法众多，包括多义树传播方法（Poly tree Propagation）、桶排除法（Bucket Propagation）、团树推理方法（Clique Tree Propagation）等，这类方法的特点是计算量随节点数增加而呈指数增长；后者则试图在计算量和计算精度上做一个折中，既保证工程实际的要求也能满足进行实时计算。

3 贝叶斯网络法评估变电站主接线可靠性

前文叙述了贝叶斯网络的基本概念，对变电站的主接线进行选择最重要是找到可用度最高的电气主接线方式。以两种常用变电站主接线为例，叙述贝叶斯网络法在变电站电气主接线优选中的应用。对电气主接线可用度进行计算时，作如下假设[14]:

1. 电气元件只有两种状态，即正常状态和故障状态，并认为元件为可修复元件，系统故障便退出运行，进行检修。检修完毕后立即恢复正常工作状态。

2. 各元件发生故障是独立的。

3. 只考虑系统发生单一故障，不考虑二重故障及二重以上故障。

两种常用变电站的电气主接线[14]如图2所示。

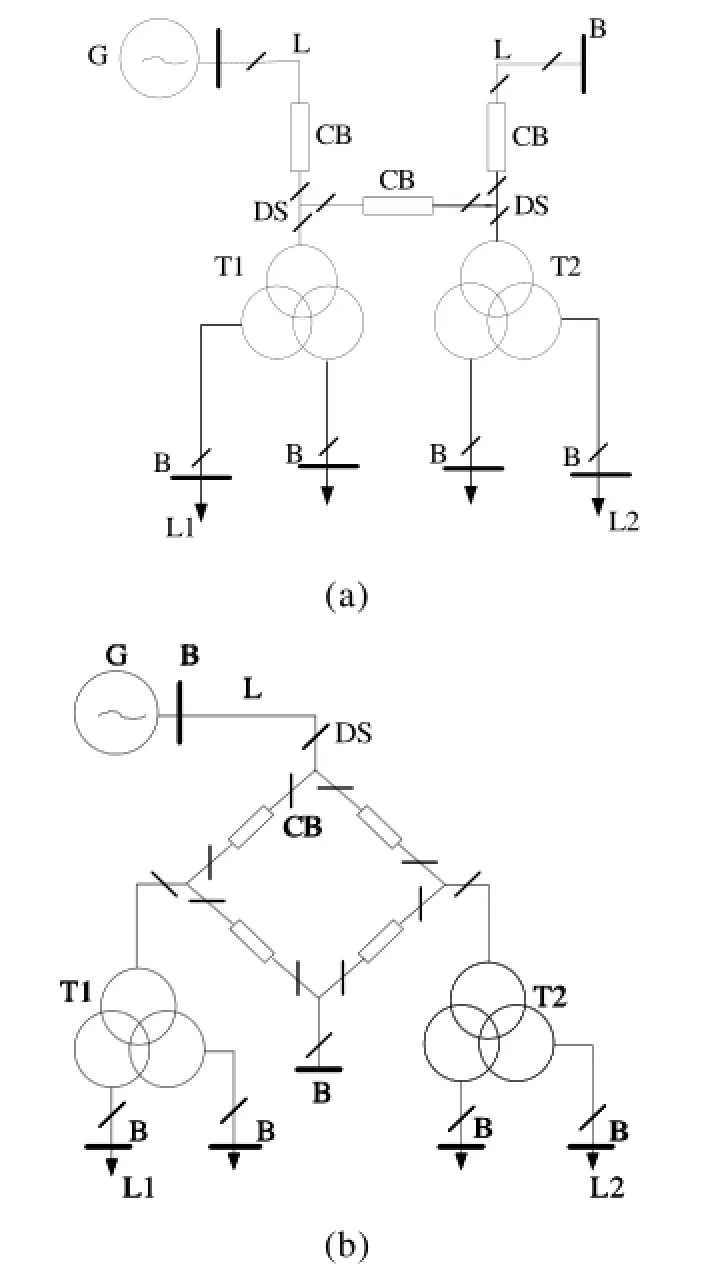
图2 变电站的电气主接线图Fig.2 The main electrical connection diagram of substation

为便于区别，设定图2（a）主接线方式为a电气主接线方式，所示系统为a电气系统。图2（b）主接线方式为b电气主接线方式，所示系统为b电气系统。图2中CB表示断路器（circuit breaker），T表示变压器（transformer），DS表示隔离开关（disconnect switch），L表示线路（line），B表示母线（bus）。电气设备可靠性指标[14]见表1。

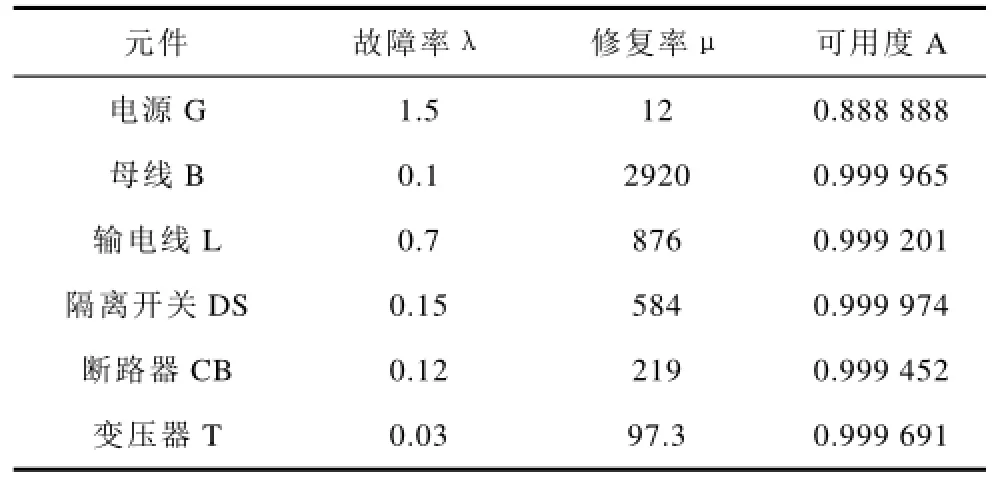
表1 电气设备的可靠性指标Tab.1 The reliability index of electrical equipment

故障率、修复率和可用度均是评价电气元件可靠性的重要指标。故障率是产品工作到t时刻后的单位时间内发生故障的概率。修复率是修理时间已达到某个时刻但尚未修复的产品，在该时刻后的单位时间内完成修理的概率。可修复元件中，通常采用可用度表征元件可以利用的程度，可以分为稳态可用度和瞬态可用度。稳态可用度常用于发展规划可靠性评估[15]。本文的可用度指稳态可用度。元件的可靠度和维修度均服从指数分布时，稳态可用度的计算公式为

图2的电气主接线图反映了变电站内的电气设备实际连接关系，在分析变电站的可靠性时，常将电气主接线图转化为布尔代数分析图或工程计算用的逻辑关系图，即从可靠性的角度，按照逻辑关系把电气设备用方块表示，并根据可用度公式及连接关系计算出每个方块的可用度。上述两种变电站电气主接线的逻辑关系图如图3所示。

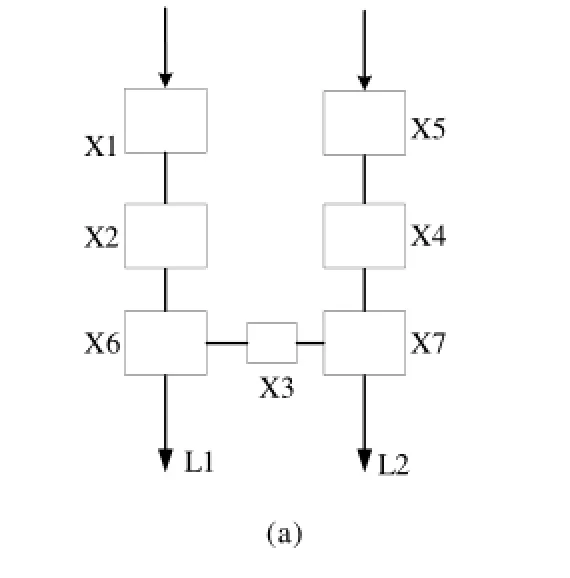
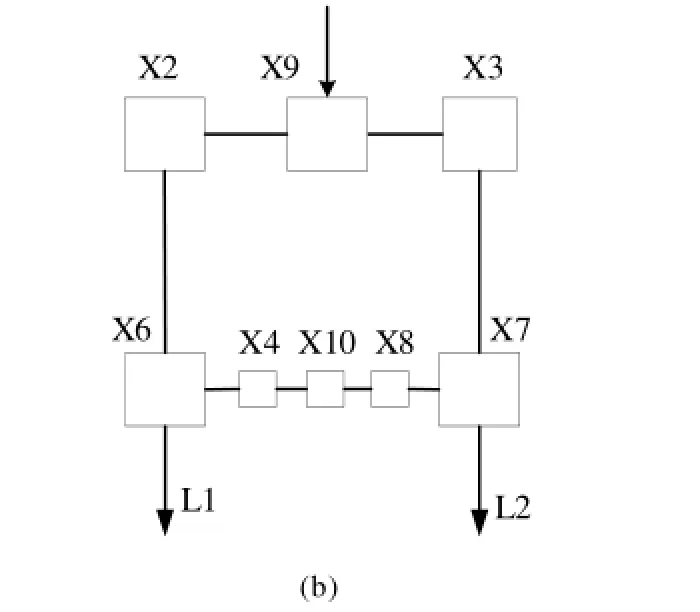
图3 变电站电气主接线的逻辑关系图Fig.3 The logic block diagram of substation main electrical connection

图3 中的方块为电气元件的组合。X1为发电机（G）、母线（B）、断路器（CB）和输电线（L）的串联组合；X2，X3，X4，X8均表示断路器（CB）；X5为输电线（L）、母线（B）和隔离开关（DS）的串联组合；X6，X7为变压器（T）、母线（B）和隔离开关（DS）的串联组合；X9为发电机（G）、母线（B）、输电线（L）和隔离开关（DS）的串联组合；X10为输电线（L）、母线（B）和隔离开关（DS）的串联组合。由于方块均由电气元件串联而成，根据串联系统的可靠性计算公式RS=∏Ri，可得各方块的可用度，计算结果见表2。

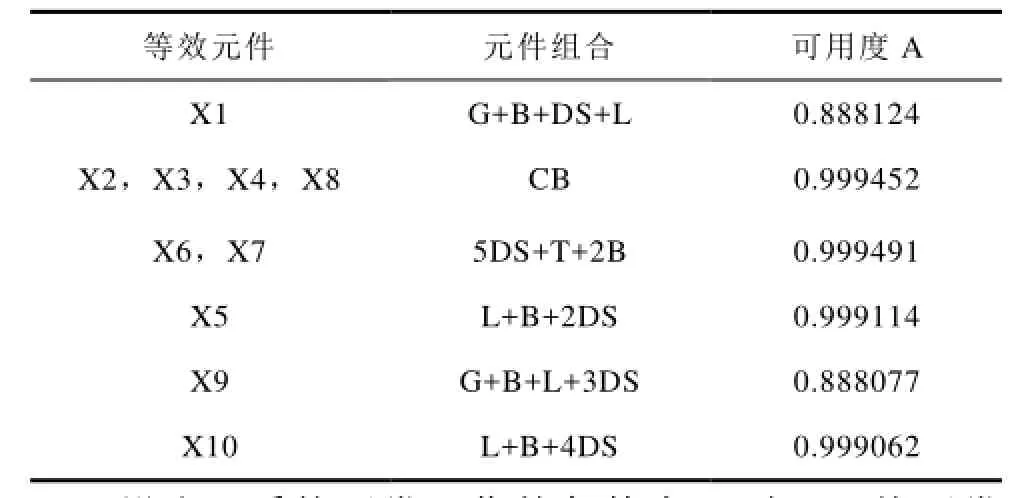
表2 等效元件的可靠性指标Tab.2 The reliability index of equivalence component

设定a系统正常工作的条件为L1与L2均正常供电。对于变电站电气主接线这样较为复杂的系统，不能直接根据电网的物理拓扑结构和串并联思想建立贝叶斯网络，需要先找到它的最小路集，以最小路集作为过渡，建立贝叶斯网络。a系统负荷L1正常供电，从母线到负荷点有两条路径，分别为X1-X2-X6和X5-X4-X7-X3-X6，记为Y1和Y2。方块X6为其公共节点，它的可靠性直接关系到负荷L1的可靠性，应单独考虑。负荷L2正常供电，从母线到负荷点有两条路径，分别为X1-X2-X6-X3-X7和X5-X4-X7，同样，方块X7应单独考虑。因此，a电气主接线的贝叶斯网络图如图4所示。

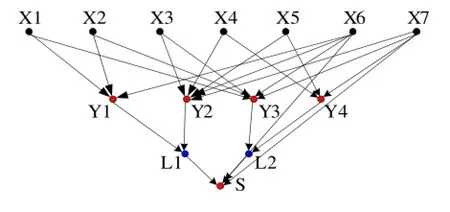
图4 a主接线贝叶斯网络Fig.4 The Bayesian Network of electrical connection a

由于对每一最小路径而言，任一元件发生故障，最小路径则故障，所以，节点Y1、Y2、Y3、Y4为“与”节点类型。用“红色”标记。两条最小路径有一条正常工作，负荷L1则正常工作，所以，负荷节点L1、L2为“或”节点类型。用“蓝色”标记。状态L1，L2分别反映负荷L1，L2供电情况，L1=1，表示负荷L1供电正常。由设定的系统正常工作条件可知，系统总节点为“与”节点。S=1，表示系统工作正常。根据贝叶斯网络及节点类型，可得出系统正常的概率为:

则系统故障的概率为:

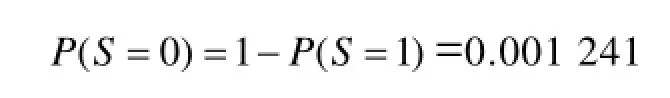
由前文可知，贝叶斯网络法的特点是可以计算系统发生故障时，每个电气元件故障的概率大小。a系统故障时，各等效元件故障的概率见表3。

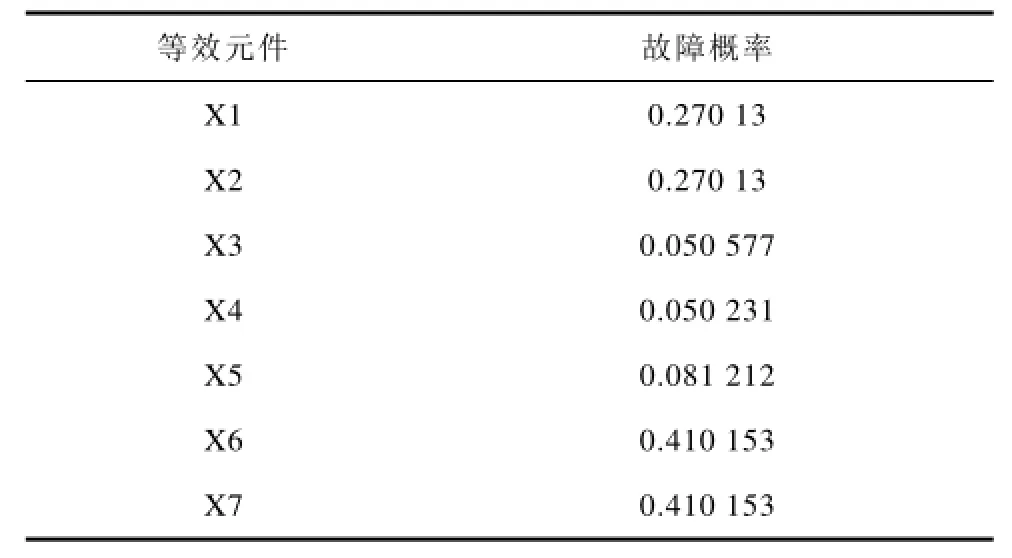
表3 a系统发生故障各等效元件故障概率Tab.3 The fault rate of equivalence component on the condition of system a fault

根据表3中数据可知，若a变电站电气主接线系统发生故障，方块6，7中电气元件发生故障的概率最大，变电站维修人员可以根据元件发生故障概率的大小依次检查。

设定b图系统正常工作的条件仍为L1、L2均供电正常。负荷L1正常供电，从母线到负荷点的两条路径X9-X2-X6和X9-X3-X7-X8-X10-X4-X6，记为Y1和Y2。负荷L2正常供电，从母线到负荷点的两条路径分别为X9-X2-X6-X4-X10-X8-X7和X9-X3-X7，记为Y3和Y4。因此，b电气主接线的贝叶斯网络图如图5所示。

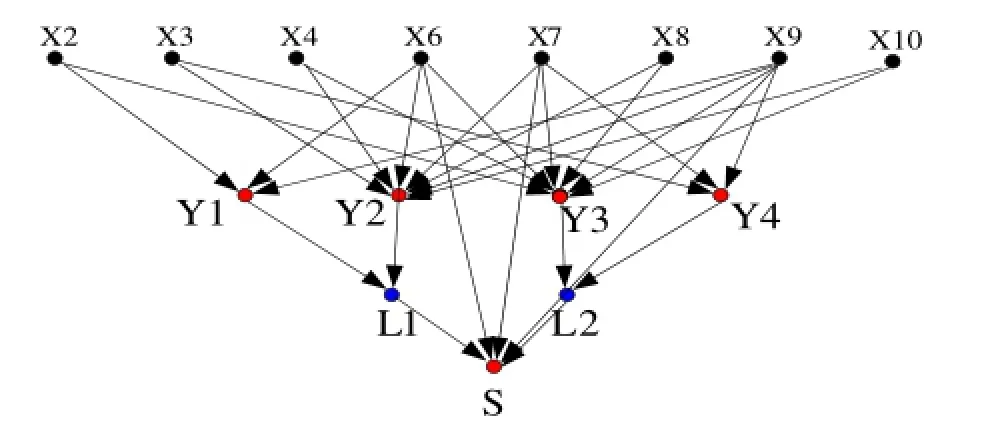
图5 b主接线贝叶斯网络Fig.5 The Bayesian Network of electrical connection b

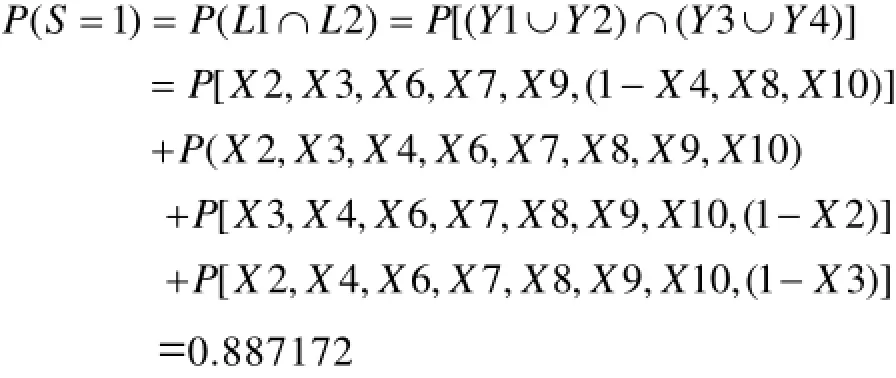
系统故障的概率:

根据贝叶斯公式，计算b系统电气主接线故障时各等效元件故障的概率见表4。

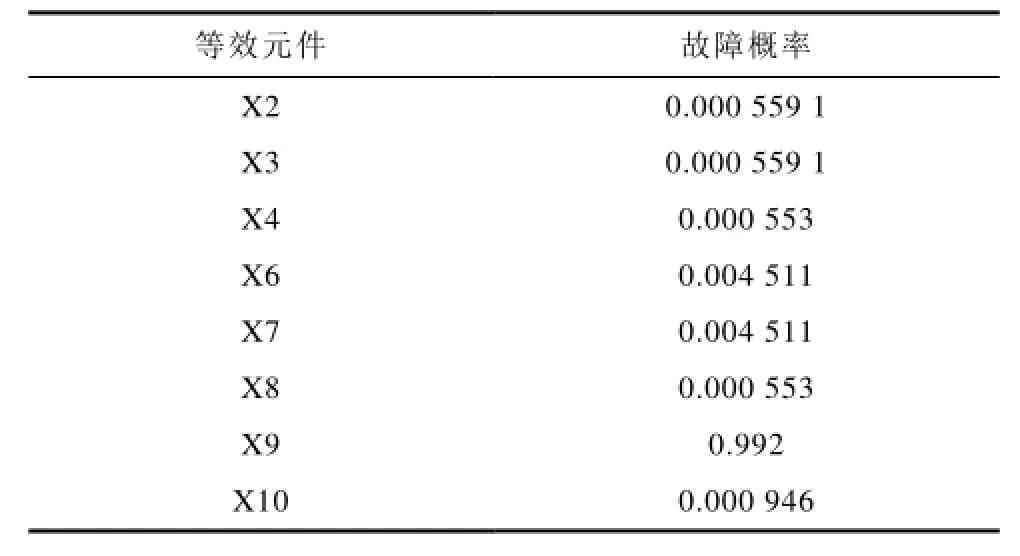
表4 b系统发生故障各电气元件故障概率Tab.4 The fault rate of equivalence component on the condition of system b fault

由表4数据可知，b变电站电气主接线故障，方块9中电气元件故障的概率最大，为99.2%。造成此结果的原因一方面是方块9为此接线方式的中枢节点，此方块故障，系统必故障。另一方面是方块9的可用度较低，仅为0.888077。所以，方块9为b主接线的薄弱环节。若想提高此接线方式的可靠性，应重点提高方块9中元件的可靠性。

对比两种接线方式的系统故障概率，显然a主接线可用度要高于b主接线方式，而b主接线方式发生故障的主要原因是方块9中元件的故障，维修简单。若两种主接线方式中各电气元件可靠性指标没有明显改变，在变电站进行主接线选择时，应优先选择a主接线方式。

4 结论

基于贝叶斯网络法进行变电站电气主接线方式的可靠性评估与方案优选，不仅可以计算出各种备选主接线方式的可用度，还可计算出系统故障时每个电气元件故障概率的大小。对于变电站维修人员而言，系统发生故障时，可以根据元件发生故障概率的大小依次排查，大大减少检修工作量；对于变电站的建设和改造而言，可以根据故障概率大小对电气元件进行选择、更换，有效节约变电站改造成本，并从根本上提高变电站主接线部分的可靠性。

[1] 李明, 韩学山, 王勇, 等. 变电站状态检修决策模型与求解[J]. 中国电机工程学报, 2012, 32(25): 196-202.

Li Ming, Han Xueshan, Wang Yong, et al. Decisionmaking model and solution of condition-based maintenance for substation[J]. Proceedings of the CSEE, 2012, 32(25): 196-202.

[2] Yang F, Kwan CM, Chang CS. Multi-objective evolutionary optimization of substation maintenance using decision-varying Markov model[J]. IEEE Transactions on Power Systems, 2008, 23(3): 1328-1335.

[3] 曹楠, 李刚, 王冬青. 智能变电站关键技术及其构建方式的探讨[J]. 电力系统保护与控制, 2011, 39(5): 63-68.

Cao Nan, Li Gang, Wang Dongqing. Key technologies and construction methods of smart substation[J]. Power System Protection and Control, 2011, 39(5): 63-68.

[4] 陈晨, 刘俊勇, 刘友波, 等. 一种考虑变电站内部的电力系统可靠性分析[J]. 电力自动化设备, 2015, 35(2): 103-109.

Chen Chen, Liu Junyong, Liu Youbo, et al. Power system reliability analysis considering substation interior[J]. Electric Power Automation Equipment, 2015, 35(2): 103-109.

[5] 姚成玉, 陈东宁, 王斌. 基于T-S故障树和贝叶斯网络的模糊可靠性评估方法[J]. 机械工程学报, 2014, 50(2): 193-201.

Yao Chengyu, Chen Dongning, Wang Bin. Fuzzy Reliability assessment method based on T-S fault tree and bayesian network[J]. Journal of mechanical engineering, 2014, 50(2): 193-201.

[6] MENTES A, HELVACIOGLU I H. An application of fuzzy fault tree analysis for spread mooring systems [J]. Ocean Engineering, 2011, 38(2): 285-294.

[7] 霍利民, 朱永利, 范高锋, 等. 一种基于贝叶斯网络的电力系统可靠性评估新方法[J]. 电力系统保护与控制, 2003, 27(5): 36-40. Huo Limin, ZhuYongli, Fan Gaofeng, et al. A new method for reliability assessment of power system based on bayesian networks[J]. Power System Protection and Control, 2003, 27(5): 36-40.

[8] 李俭川, 胡茑庆, 秦国军, 等. 贝叶斯网络理论及其在设备故障诊断中的应用[J]. 中国机械工程, 2003, 14(10): 896-900.

Li Jianchuan, Hu Niaoqing, Qin Guojun, et al. Bayesian network and its applications for device fault diagnosis[J]. China Mechanical Engineering, 2003, 14(10): 896-900.

[9] Charniak E. Bayesian Networks without Tears. AI Magazine, 1991, 12(4): 50-63.

[10] Pearl J. Graphical Models for Probabilistic and Causal Reasoning. In: The Computer Science and Engineering Handbook. Kluwer Academic Publishers, 1997: 697-714.

[11] 尹晓伟, 钱文学, 谢里阳. 系统可靠性的贝叶斯网络评估方法[J]. 航空学报, 2008, 29(6): 1282 -1289.

Yin Xiaowei, Qian Wenxue, Xie Liyang. A Method for System Reliability Assessment Based on Bayesian Networks[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1282 -1289.

[12] 赵文清, 王强, 牛东晓. 基于贝叶斯网络的电抗器健康诊断[J]. 电力自动化设备, 2013, 33(1): 40-43.

Zhao Wenqing, Wang Qiang, Niu Dongxiao. Reactor health diagnosis based on Bayesian network[J]. Electric Power Automation Equipment, 2013, 33(1): 40-43.

[13] 周忠宝, 董豆豆, 周经伦. 贝叶斯网络在可靠性分析中的应用[J]. 系统工程理论与实践, 2006, (6): 95-100.

Zhou Zhongbao, Dong Doudou, Zhou Jinglun. Application of bayesian networks in reliability analysis[J]. Systems Engineering-theory & Practice, 2006, (6): 95-100.

[14] 程林, 何剑. 电力系统可靠性原理和应用[M]. 北京:清华大学出版社, 2015: 356-358.

[15] 齐先军, 史新红, 丁明, 等. 电力系统元件稳态可用度的非精确统计推断[J]. 中国电机工程学报, 2014, 34(13): 2108-2115.

Qi Xianjun, Shi Xinhong, Ding Ming, et al. Imprecise Statistical Inference for Steady-state Availability of Components in Power Systems[J]. Proceedings of the CSEE, 2014, 34(13): 2108-2115.

Reliability Assessment and Optimization of Main Electrical Connection of Substation

Xu Xiaoning
（ZheJiang Guangsha College of Applied Construction Technology Dongyang 322100）

In view of the limitations of traditional reliability assessment methods about on the main electrical connection of the substation, Bayesian network was applied to the reliability assessment and optimization of main electrical connection of substation. For this purpose, the example selected of two kinds of common main connection mode. Firstly, decomposed system according to the structure and function and obtained the logic diagram. Secondly, determined the minimum path from generator to the load and established the Bayesian networks which the function module was the node. Finally, calculated the system availability on basis of the Bayesian networks and found the weak links of reliability in the two main electrical connection. Calculation results show that the Bayesian network can help engineers to choose substation main electrical connection and guide maintenance work in the future, has a greater practical significance.

Substation, Main electrical connection, Reliability assessment, Scheme Optimization, Bayesian Networks

TM63; TM715

2014-- 改稿日期 2014--

徐小宁 男，1962出生，工学硕士，副教授，研究方向为电力系统及其自动化、新能源、电磁场理论及其工程应用。