新型旋转电磁热机流体流动与传热的耦合计算与实验

杜 海 曲延滨 张 鹏

新型旋转电磁热机流体流动与传热的耦合计算与实验

杜 海 曲延滨 张 鹏

（哈尔滨工业大学电气工程与自动化学院 哈尔滨 150001）

针对一种新型旋转电磁热机内部流体流动和传热的特点，建立了其三维流体流动和传热耦合计算的物理模型和数学模型，利用经验公式确定了热机内部气隙的等效导热系数以及各部件表面散热系数，采用有限体积法对热机内部的流体流动与传热进行耦合仿真计算，确定了热机在不同工作条件下的出水温度及内部温度分布。搭建了基于该热机的热水升温实验平台并进行实验测试，并将耦合场的数值计算结果与实验测试结果进行对比分析，为热机的结构设计、优化、及合理稳定运行提供必要的理论和实验依据。

旋转电磁热机 轴向磁场 有限体积法 温度场

1 引言

旋转电磁热机是一种新型能量转换装置，能够将风力涡轮机、水轮机、电动机等动力装置输出的机械能作为能量输入，通过旋转耦合磁场转换为涡流损耗热能，并最终以水为传热介质进行热能传递。同时，旋转电磁热机还可综合利用其内部的旋转磁场、温度场对受热水媒质进行软化处理[1-3]。

传统旋转电磁热机主要采用径向磁场结构设计，即转子永磁体产生的磁通沿径向穿过定子，在定子中形成涡流并产生涡流损耗[4]。为了提高永磁体和定子材料利用率，可采用中间定子的双转子结构设计，该热机的定子呈圆筒形结构，热机结构设计复杂，加工制造难度较大，且空间利用率较低。

本文提出一种轴向磁场结构的旋转电磁热机，该热机结构简单紧凑，空间利用率高，且可同轴并联构成机组，更易应用于工程实际。在文献[5-8]的研究基础上，基于新型旋转电磁热机的结构特点，建立了该热机传热系统内三维流体场与温度场耦合求解的数学模型和物理模型，采用有限体积法分析其热水升温性能，同时，搭建以该热机为基础的热水升温实验平台并进行了相关实验研究，将耦合场计算结果与实测结果进行比较分析，为旋转电磁热机综合物理场的准确计算提供理论和实验基础。

2 结构及工作原理

轴向磁场旋转电磁热机同样采用中间定子的双转子结构，但是其定、转子都设计为圆盘形状，如图1所示。转子材料为块状导磁铁心，表贴的永磁体沿轴向充磁，磁极交替配置。圆盘定子采用纯铜材料，内部水路设计为螺旋管路。

图1 轴向磁场旋转电磁热机示意图Fig.1 Scheme of rotating induction heater with axial-field configuration

该结构热机只有一个机械能输入的端口，可将外部动力系统产生的机械能传递给转子，形成转子的动能。多极永磁转子的旋转运动形成旋转磁场，磁极交替穿过定子导体，定子导体各处磁通量的变化会生成感应电动势，在感应电动势作用下形成涡流，并产生涡流损耗热能。这些热能过定子中的传热工质带走，不断消耗转子动能，从而实现机械能到热能的能量转换。该热机能量转化过程的实质就是利用法拉第电磁感应原理把运动物体的动能转化为电能，电能最终转化为热能散发掉[9]。同时，旋转磁场对定子传热管道内的传热工质（水媒质）还具有磁化作用。

3 流体流动及温度场的数值计算

3.1数学模型

该热机以定子导体的涡流损耗为热源，其热量传递过程主要有两个环节:一是定子导体的大部分热量通过热传导方式传递到管道内壁，再通过热对流方式传递给水媒质，实现对水媒质的升温作用；二是定子导体小部分热量利用对流和辐射方式通过气隙传递给永磁体和转子，该热量传递的结果会使得永磁体升温，改变永磁体的磁特性，从而影响热机的工作性能。热机温度场分布主要与传热管道内水媒质的对流换热及气隙的传热相关。系统内的流体流动与传热满足动量守恒定律、质量守恒定律以及能量守恒定律。以上守恒定律可利用如下控制方程描述。

3.1.1 紊流k-ε数学模型

当流体处于不可压缩且稳定流动状态时，根据流体力学理论，一般采用最广泛的标准k-ε数学模型，其通用控制方程为:

式中 ρ——流体密度；

φ、V——通用变量；

Γ——扩散系数；

S——源项。

3.1.2 三维热传导方程

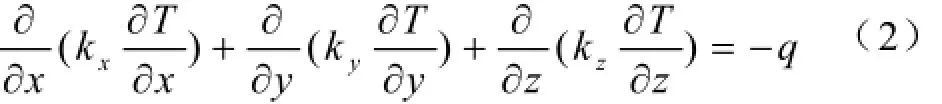
式中 kx、ky、kz——分别为x、y、z方向的导热系数(W/m·K)；

q——内部热源密度(W/m3)；

T——温度(K)。

3.1.3 能量守恒方程

定子传热管道内流动系统的热交换过程必须满足能量守恒基本定律，其方程可如下描述:

目前，国内外针对复杂结构电磁装置（比如风冷或水冷电机）温度场的计算与分析，主要采用有限体积方法[10-12]。在计算流体力学领域中，有限体积法是一种应用最为广泛的数值分析方法。本文对以上各控制方程采用有限体积法求解，可较准确的获得热机内部三维流场和温度场分布情况。

式中 u、v、w——流体的速度分量；

p——流体压力；

h——流体的比焓；

U——流体的速度矢量；

λ——流体的导热系数；

Φ——耗散函数；

Sh——流体的内热源及由粘性作用流体机械能转换为热能的部分。

以上三个方程都可以表示为统一的通用形式:

3.2物理模型

轴向磁场旋转电磁热机数值计算的物理模型是以实验样机为参照建立的。该模型求解区域包括转子、气隙、定子及其内部水路，结构参数变量如图1所示，参数设置如表1所示。三维网格剖分结果如图2所示。定子内水套结构如图3所示。

图2 轴向磁场电磁热机求解域网格剖分Fig.2 Mesh of solution region of rotating induction heater with axial-field configuration

表1 实例结构参数Tab.1 Parameters of example

图3 轴向磁场电磁热机定子中水路分布示意图Fig.3 Sketch of water channel in stator of rotating induction heater with axial-field configuration

3.3基本假设和边界条件

为简化分析，对轴向磁场旋转电磁热机的求解模型做以下基本假设:（1）根据热机实际工作情况，由雷诺系数Re确定流动状态，当Re＞2300时采用紊流模型对流体场求解，而Re＜2300时采用层流模型求解；（2）由于传热管道内流体流速远小于声速，因此将其作为不可压缩流体考虑；（3）忽略浮力和重力对传热管道内流体场的影响；（4）只研究传热管道内流体流速的稳定状态，即认定流体流动为定常流动，因而控制方程中不含有时间项；（5）不考虑定子材料物性参数随温度变化的影响，忽略流体物性参数的变化；（6）以定子为唯一热源，并假定热源密度均匀分布。

根据热机内定子传热管道的结构、流体流动和传热的特点，给出以下边界条件:（1）给定速度入口边界条件，以及压力出口边界条件。（2）定子作为施加的恒定热源，热源大小为

式中 Pe——定子涡流损耗(W)；

V——定子体积(m3)。

（4）绝热边界条件:

式中 kn——垂直于绝热面的导热系数；

sW——求解域绝热面，为转子内侧圆周表面。

（5）传热接触面边界条件:

式中 h——表面散热系数(W/m2·℃)；

Tf——流体温度(℃)；

sD——求解域中的散热面，包括两个转子轴向两端的外表面，以及定子在r=Ro和r=Ri处的圆周面；

3.4气隙导热系数及表面散热系数的确定

3.4.1 气隙导热系数的确定

对于轴向磁场电磁热机，定子与双转子均为中空的圆盘形状，圆盘之间的气隙存在运动气体的对流换热，在此引入有效导热系数将其等效为静止气体的热传导。为方便运算作近似处理，忽略转子圆盘在径向上线速度的差别。气隙的等效导热系数与气体的流动状态相关，这里利用特依洛尔数Ta代替雷诺系数Re来判定气隙中气体的流动状态[13]:

式中 Rm——为圆盘的平均半径(m)，Rm=(Ri+Ro)/2；

δ——气隙长度(m)；

ω——转子角速度(rad/s)；

υ——空气运动粘度(m2/s)。

当Ta≤41.2时，气隙中气体流动形态为层流，此时气隙通过热传导传递热量，热交换强度与转速无关。气隙中努赛尔数Nu为常数，可以认为气隙中导热系数即为空气的导热系数λk。当Ta≥41.2时，气隙中的气体为湍流流动，此时气隙中的努赛尔数Nu如下式所示:

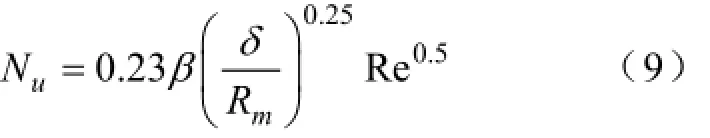
式中 β——借鉴电机中转子表面粗糙度的经验系数，β取值为1.15～1.25；

Re——气隙中的雷诺数，Re=ωRmδ/υ；

由此，气隙中气体流动处于紊流状态时的等效导热系数计算公式为:

3.4.2 转子外表面散热系数的确定

转子盘在旋转过程中，轴向两端外表面处于空气受迫对流散热状态，将其视为纵掠平板对流传热。转子盘面的散热系数与表面空气运动状态有关，因此，首先依据气体流动雷诺系数Re来判断流动状态。转子盘面处空气雷诺系数Re可近似定义为[14]:

式中 L——转子盘等效的特征长度(m)，此处取L=2πRm；

ρ——空气密度(Kg/m3)。

根据雷诺系数判定转子轴向两端外表面的散热系数[15]。当Re＜500 000时，转子盘面的空气流动为层流状态，其表面散热系数为:

式中 Pr——普朗特数，与环境温度有关，在此取Pr=0.7；

λ——空气导热系数(W/(m·K))；

当Re＞500 000时，转子盘面的空气流动为紊流状态，其表面散热系数为:

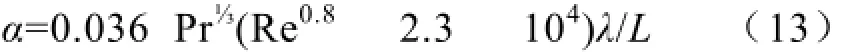
转子外圆周表面也处于空气受迫对流散热状态，确定其散热系数可参考转子轴向两端外表面散热系数计算的方法。在计算过程中，公式(11)～公式（13）中的特征长度L应取值为L=2πRo。

3.4.3 定子外圆周表面的散热系数的确定

定子外圆周表面的散热系数可按以下经验公式计算:

式中 v——转子外圆周的线速度(m/s)。

以上等效导热系数及散热系数与多种因素有关，其相关公式都是具有经验或半经验性质，这些公式所给出的只能是大致估算值，在针对计算实例的有限体积法仿真过程中，要根据流体与导热体的实际情况做出修正。定子传热管道的传热接触面的散热系数不必进行类似计算，由于流体域和定子固件的交界面为耦合传热，在有限体积法仿真计算过程中，其散热系数由流体流动方程、能量方程和传热方程经过耦合迭代得到。

3.5数值计算结果与实验分析

在数值求解过程中根据实验过程的实际情况来设定热源大小、进口流速、进口温度等条件。其中，流体进口温度为实测的291.15K，管道内流体平均流速测得为0.43m/s，计算所得雷诺系数Rec=662，因此在该流速下管道内流体流动状态为层流，计算中选用Laminar模型。热机在500rpm转速时测得功率157W，计算可得热源大小为2 854 545W/m3。图4为轴向磁场电磁热机定子传热管道内的流体的三维温度场分布。从图中可以看出，流体最高温度为320.5K，位于螺旋管道内侧。当流体从定子外侧螺旋管道流出，由于和进口螺旋管道的流体存在一定程度的热交换，使得流体出口温度降低到309.9K。若在样机定子的设计中，将进口螺旋管道和出口螺旋管道之间进行隔热处理，可以进一步提高出口水温。图5为盘式双转子表面的温度分布，转子内侧的温度最高，温度范围在318.3～320.4K之间。

图4 流体三维温度场分布Fig.4 3-D temperature distribution of water

图5 转子表面温度分布Fig.5 Temperature distribution of surface of dual-rotor

图6 热机样机的主要部件照片Fig.6 Photo of components of prototype heater

在此样机基础上搭建热水升温实验平台，该实验平台主要包括轴向磁场旋转电磁热机、驱动电机、变频控制器、转矩传感器、扭矩测量仪、转速测量仪、温度传感器、温度巡检仪、水泵、连接管路与水箱。其中，电磁热机、转矩传感器与驱动电机同轴安放，转矩传感器位于电磁热机与驱动电机之间，扭矩测量仪显示输入电磁热机的转矩大小；变频控制器可驱动电机在不同转速下稳定运行；热机转速由转速测量仪获得；水泵将进水水箱中的水通过管路送入热机，经过热机加热升温后流向出水水箱；在进水水箱和传热管道出口处安放温度传感器，通过温度巡检仪读取进水、出水的温度。实验平台现场照片见图7。

测得定子管道内水路流速为0.43m/s，进水水温为291.15K(18℃)。该热机定子的用铜量为5.5 105m3。热机在不同转速下测得的转矩，以及计算所得的热功率和热源大小如表2所示。

图7 旋转电磁热机实验测试平台照片Fig.7 Photo of rotating induction heater test system

表2 不同转速下的转矩、热功率及热源Tab.2 Torque, thermal power and heat source at different speed

图8为样机在不同转速下出水温度的实测值与流体传热耦合数值计算的结果。当热机转速达到1 000rpm时，通过有限体积法计算得到定子管道内的最高温度接近100℃，然而基本假设中忽略了流体物化参数的变化，即没有考虑流体在高温时由液相转为气相的问题，因此当热机转速超过1 000rpm后，数值计算所得结果不具有参考性。

图8 旋转电磁热机升温实验结果Fig.8 Heating experiment results of rotating induction heater

从图8中可以看出，在较低转速范围内，数值计算结果与测试值较为接近，且实测数据要小于数值计算的结果，而随着转速的升高，数值计算结果与实测值相差越来越大。主要有以下原因:一是随着转速升高，定子热功率增大，随之转子温度有一定程度升高，虽然永磁体处于可正常工作的温度范围内，但在数值计算过程中并没有考虑永磁体磁特性随温度变化的影响；二是在数值计算过程中，忽略了转子与转轴之间的热量传递，该热量损失使得实测值要偏小；三是数值分析模型忽略了出口管路的长度，而样机的出口管路也存在热量散失，使得测量的出口温度值偏低。造成实测值与数值计算偏差的三个原因中，第一个原因是主要原因，并且使得偏差随转速升高而增大。在热机实际应用过程中，也要注意转子永磁体的温度不能过高，否则轻则会降低致热、传热效率，严重会导致永磁体高温失磁，使得热机无法工作。

4 结论

本文提出一种新型旋转电磁热机，即轴向磁场旋转电磁热机，采用有限体积法对热机内部的流体流动和传热进行耦合计算与分析。数值分析与实验测试结果证实该热机升温效果显著，且在正常工况转速范围内（0～900rpm），出水温升实测结果与数值计算结果较为一致，表明该流体传热耦合分析方法的正确性，为其综合物理场的准确计算及热机换热设计提供了理论和实验基础。该热机可在集中供热管网系统中可作为辅助热源，并起到软化水质，阻垢、抑垢的作用；在高寒、高纬度地区或北方沿海、海岛地区，可设计为独立供暖系统，直接利用苦咸水、海水等极端水质进行加热供暖，其装备设计研究具有广阔的应用前景。

[1] 张鹏, 郭斌, 程树康, 等. 旋转电磁加热技术及其腐蚀结垢研究[J]. 电工技术学报, 2007, 22(Suppl.2)：195-198.

Zhang Peng, Guo Bin, Cheng Shukang, et al. Effect of rotating electromagnetic heating technology on corrosion and scale[J]. Transactions of China Eletrotechnical Society, 2007, 22(Suppl.2)： 195-198.

[2] 陈磊, 柴凤, 程树康. 新型旋转电磁热机对水媒质磁化作用机理初探[J]. 微电机, 2009, 42(9)： 65-68.

Chen Lei, Chai Feng, Cheng Shukang. Fundamental research on magnetization of water medium by novel rotating electromagnetic heating machine[J]. Micromotors, 2009, 42(9)： 65-68.

[3] 陈磊, 柴凤, 裴宇龙, 等. 新型旋转电磁热机三维电磁场方程的求解及相关电磁参数的研究[J]. 电工技术学报, 2011, 26(7)： 147-153.

Chen Lei, Chai Feng, Pei Yulong, et al. Solution of the 3D electromagnetic equation and research on related electromagnetic parameters of the novel rotational electromagnetic heating machine[J]. Transactions of China Eletrotechnical Society, 2011, 26(7)： 147-153.

[4] 杜海, 张鹏, 曲延滨. 一种双转子电磁热机及其磁场和涡流分析[J]. 电机与控制学报, 2013, 17(5)：51-56.

Du Hai, Zhang Peng, Qu Yanbin. A Dual-rotor Electromagnetic heat engine and its magnetic field and eddy current analysis[J]. Electric Machine and Control, 2013, 17(5)： 51-56.

[5] 李伟力, 杨雪峰, 顾德宝, 等. 多风路空冷汽轮发电机定子内流体流动与传热耦合计算与分析[J]. 电工技术学报, 2009, 24(12)： 24-31.

Li Weili, Yang Xuefeng, Gu Debao, et al. Calculation and analysis of fluid flow and heat transfer of aircooled turbo-generator with multipath ventilation[J]. Transactions of China Eletrotechnical Society, 2009, 24(12)： 24-31.

[6] 路义萍, 马贤好, 李伟力. 空冷汽轮发电机转子风道结构对传热的影响[J]. 中国电机工程学报, 2007, 27(17)： 61-66.

Lu Yiping, Ma Xiaohao, Li Weili. The effect of geometry factors on heat transfer of rotor’s cooling duct of large turbo generator with air-coolant[J]. Proceedings of the CSEE, 2007, 27(17)： 61-66.

[7] 李伟力, 孙宏丽, 于海涛. 空冷汽轮发电机定子绕组异结构下的不饱和同步电抗、绕组内涡流场与温度场的计算与分析[J]. 电工技术学报, 2011, 26(2)：50-58.

Li Weili, Sun Hongli, Yu Haitao. Calculation and analysis of unsaturated synchronous reactance, eddy current distribution in windings and temperature field for air cooled turbo-generator with different stator windings structures[J]. Transactions of China Eletrotechnical Society, 2011, 26(2)： 50-58.

[8] 路义萍, 陈朋飞, 邓海燕, 等. 某新型通风方式空冷汽轮发电机转子三维温度场[J]. 电工技术学报, 2011, 25(11)： 29-35.

Lu Yiping, Chen Pengfei, Deng Haiyan, et al. Temperature field of one air-cooled turbo-generator rotor with new ventilation type[J]. Transactions of China Eletrotechnical Society, 2011, 25(11)： 29-35.

[9] 江善林. 高速永磁同步电机的损耗分析与温度场计算[D]. 哈尔滨： 哈尔滨工业大学, 2010： 121-122.

Jiang Shanlin. High-speed Permanent Magnet Synchronous Motor Loss Analysis And Temperature Field Calculation[D]. Harbin： Harbin Institute of Technology, 2010： 121-122.

[10] 张晓晨, 李伟力, 邱洪波, 等. 超高速永磁同步发电机的多复合结构电磁场及温度场计算[J]. 中国电机工程学报, 2011, 31(30)： 85-92.

Zhang Xiaochen, Li Weili, Qiu Hongbo, et al. Calculation of electromagnetic field and temperature field in super high speed permanent magnet generator with composite structures[J]. Proceedings of the CSEE, 2011, 31(30)： 85-92.

[11] 魏静微, 杨崑, 谢颖, 等. 高转差异步发电机转子的三维温度场及旋转热管的应用[J]. 电机与控制学报, 2011, 15(7)： 82-86.

Wei Jingwei, Yang Kun, Xie Ying, et al. 3D Temperature field of high slip asychronous generator rotor and analysis of rotating heat tube[J]. Electric Machines And Control, 2011, 15(7)： 82-86.

[12] 路义萍, 郑国丽, 韩家德, 等. 副槽及出风口结构尺寸对汽轮发电机转子三维温度场的影响[J]. 中国电机工程学报, 2011, 31(26)： 90-96.

Lu Yiping, Zheng, Guoli, Han Jiade, et al. Effect of structure size of sub-slot and it’s air outlet on threedimensional temperature field for turbo-generator rotor[J]. Proceedings of the CSEE, 2011, 31(26)：90-96.

[13] 李伟力, 袁世鹏, 霍菲阳, 等. 基于流体传热理论永磁风力发电机温度场计算[J]. 电机与控制学报, 2011, 15(9)： 56-62.

Li Weili, Yuan Shipeng, Huo Feiyang, et al. Calculation of temperature field of pm generator for wind turbine based on theory of fluid heat transfer[J]. Electric Machines And Control, 2011, 15(9)： 56-62.

[14] 马宏忠, 耿志慧, 王庆燕, 等. 磁悬浮承重装置中发热与温升分析计算[J]. 中国电机工程学报, 2012, 32(30)： 126-131.

Ma Hongzhong, Geng Zhihui, Wang Qingyan, et al. Analysis and calculation for heating and temperature rise of magnetic levitation device[J]. Proceedings of the CSEE, 2012, 32(30)： 126-131.

[15] 李立毅, 黄旭珍, 寇宝泉, 等. 基于有限元法的圆筒型直线电机温度场数值计算[J]. 电工技术学报, 2013, 28(2)： 132-137.

Li Liyi, Huang Xuzhen, Kou Baoquan, et al. Numerical calculation of temperature field for tubular linear motor based on finite element method[J]. Transactions of China Eletrotechnical Society, 2013, 28(2)： 132-137.

Coupling Calculation and Experiment of Fluid Flow and Heat Transfer of a New Rotating Induction Heater

Du Hai Qu Yanbin Zhang peng
（School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001）

A new rotating induction heater is proposed, and its mathematical and physical model of 3-D fluid and temperature coupling field are established according to the characteristics of fluid flow and heat transfer. The equivalent coefficient of heat conductivity for airgap and the coefficient of heat transfer for surface of main components are given based on empirical formulas. The 3-D fluid and temperature coupling field are numerically calculated using finite volume method. The temperature rise of water and the temperature field in heater are determined under different working conditions. Experiment test are implemented on experiment platform for heating water by the heater. Some useful conclusions are obtained by comparing the calculation result with test value.

Rotating induction heater, axial-field, finite volume method(FVM), temperature field.

TM502

杜 海 男，1979年生，博士研究生，研究方向为基于旋转电磁效应海水淡化技术。

2014-09-10

曲延滨 男，1961年生，教授，博士生导师，研究方向为风力发电控制技术及电力电子与电力传动。