永磁同步电机转速环的一种变结构PI控制器
符 慧 左月飞 刘 闯 张 捷
永磁同步电机转速环的一种变结构PI控制器
符 慧 左月飞 刘 闯 张 捷
(南京航空航天大学自动化学院 南京 210016)
在永磁同步电机调速系统中,传统PI控制的阶跃响应存在超调的问题。采用IP控制虽可消除超调,但会使系统响应变慢,对时变输入的跟踪性能变差。为此,本文提出了一种变结构PI(Variable Structure PI,VSPI)控制器,在传统PI控制器的基础上引入输入微分前馈,并将误差比例环节与误差积分环节并联的结构改为误差的比例微分环节与积分环节串联的结构。结合遇限停止积分的抗积分饱和环节,VSPI控制在时变输入时等效于PI控制,在阶跃给定时等效于IP控制,因此,VSPI控制在解决阶跃响应的超调问题的同时提高对时变输入的跟踪精度。实验结果验证了所提控制方法的有效性和实用性。
永磁同步电机 PI IP 超调 输入微分前馈
1 引言
永磁同步电动机(Permanent Magnetic Synchronous Motor,PMSM)以其高功率/重量比、高转矩/惯量比、高效率和具有一定鲁棒性等优点,被广泛应用于工业调速系统中。传统的PMSM调速系统大多采用双环线性控制结构,内环为电流环,外环为速度环。尽管多种先进的复杂控制策略如非线性PI控制[1]、自适应控制[2-3]、模糊控制[4]、滑模变结构控制[5-6]等被应用于PMSM调速系统中,但这些非线性控制策略对处理器要求高或存在抖振等问题,还有待进一步改进。因此,在工业应用中占主导地位的控制方法仍是传统的线性PI控制。然而传统线性PI控制存在一些问题,比如控制参数整定困难、阶跃响应存在超调等。
针对传统线性PI控制时阶跃响应的超调问题,文献[7]提出采用跟踪微分器对阶跃给定安排过渡过程来实现无超调控制,但存在参数调节复杂的问题。文献[8]采用输出微分负反馈来消除超调,然而输出微分会引入噪声,影响系统性能。为抑制噪声,文献[9-11]在文献[8]的基础上将PI控制改成I控制以构成IP控制器,该方法尽管消除了超调,但对时变输入的跟踪性能变差。
本文在传统PI控制器的基础上引入输入微分前馈(Input Derivative Feedforward,IDF),将误差比例环节与误差积分环节并联的结构改为误差的比例微分环节与积分环节串联的结构,并结合遇限停止积分的抗积分饱和环节[12]设计出一种变结构PI控制器,在保证阶跃响应无超调的同时,提高了对时变输入的跟踪性能。对于时变输入,VSPI控制等效于PI控制,无扰动时的跟踪误差为零;对于阶跃给定,VSPI控制等效于IP控制,响应无超调。此外,该控制器结构简单,易于工业实现。实验结果验证了所提方法的有效性和实用性。
2 转速环PI与IP控制器
2.1PMSM的数学模型
本文研究的是表贴式永磁同步电机,其在转子磁场定向的同步旋转坐标系(d-q坐标系)下的机械运动方程为

其中,J为系统的转动惯量,kg·m2;B为系统的粘滞摩擦系数,N·m·s/rad;TL为负载转矩,N·m;Ω为机械角速度,rad/s;Kt为转矩常数,N·m/A_peak,iq为交轴电流,A。
2.2转速环PI控制器分析
采用直轴电流为零,即id*=0的矢量控制方式。由式(1)可得机械角速度状态方程为

其中,iq*为交轴电流给定值;控制增益b=Kt/J;总扰动转矩Td=Kt(iq*-iq)+TL+BΩ;扰动项a(t)=-Td/J。
选取机械角速度Ω为状态变量x1,将扰动a(t)扩张为状态变量x2,则状态方程变为

定义机械角速度给定值v与反馈值x1之差为角速度跟踪误差es,即es=v-x1,则由式(3)可得角速度跟踪误差的状态方程为

采用线性比例积分反馈控制律,即
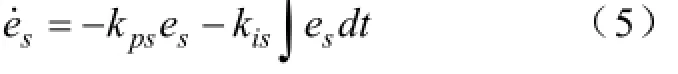
式中,kps、kis分别为控制器的比例系数和积分系数,用于控制角速度跟踪误差的衰减过程。
结合式(4)和(5)可得控制量为

式(6)中的实际状态x1可通过传感器测量或用观测器对其进行观测,状态变量x2一般不可知,故控制量修正为

为便于表述,以下将带IDF的PI控制器简称为PI控制器,以区别于传统PI控制器。
定义y为状态x1的测量值,包含实际状态x1和状态的量测噪声δns,即y=x1+δns。用y代替x1作为反馈,于是角速度跟踪误差为es=v-y,控制量为

限幅后的实际控制量为
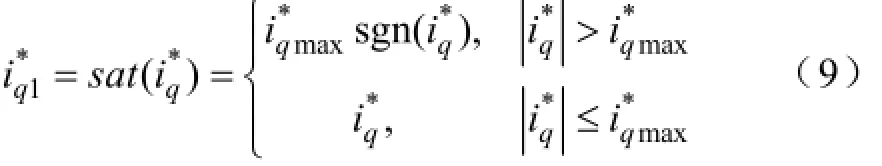
由于PI控制器中存在积分环节,为避免积分饱和造成控制性能恶化,需施加抗积分饱和环节。一般抗积分饱和采取的措施有反计算法、条件积分法等。本文选用遇限停止积分法,满足一定条件就不再进行积分项的累加,避免饱和程度的进一步加深。
综上可得转速环PI控制器的结构框图如图1所示。永磁同步电机转速PI控制系统简化结构框图如图2所示。

图1 转速环PI控制器Fig.1 PI controller of speedloop

图2 转速环系统结构框图Fig.2 Block diagram of speedloop system
为便于分析,忽略电流跟踪误差和电流限幅的影响,则由式可得

由式(3)和(10)可得闭环系统在机械角速度给定v(s)、扰动x2(s)以及测量噪声δns(s)作用下的传递函数分别为

于是,闭环系统的特征多项式为λ(s)=s2+kpss+ kis。令λ(s)为理想的特征多项式(s+ωn)2,则kps=2ωn、kis=ωn2,ωn为闭环控制系统的带宽。只要选取合适的ωn,kps和kis便唯一确定。
当无输入微分前馈或输入微分前馈不起作用时,系统在给定v(s)作用下的传递函数将变为
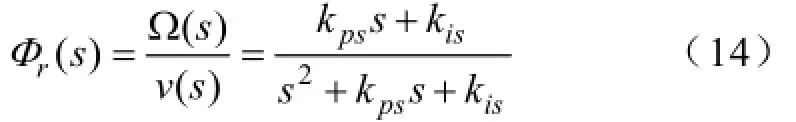
2.3转速环IP控制器分析
为解决传统线性PI控制时阶跃响应的超调问题,文献[9-11]均采用了IP控制器。为了形式统一、便于比较,本文对IP控制器作调整,调整后的结构框图如(a)所示。相比于PI控制器,IP控制器是将比例控制作用移到反馈通道中。为了便于和下文的VSPI控制器作比较,对IP控制器作等效变换,变换后的结构如(b)所示。


图3 转速环IP控制器Fig.3 IP controller of speedloop
同理可得闭环系统在机械角速度给定v(s)、扰动x2(s)以及测量噪声δns(s)作用下的传递函数分别为

当无输入微分前馈或输入微分前馈不起作用时,系统在给定v(s)作用下的传递函数变为

2.4PI控制系统与IP控制系统的性能比较
首先考虑系统的跟踪性能。对时变输入而言,输入的微分dv/dt一般不会过大,作用时间也不会过短,能够被系统响应,因此IDF可以起作用。由式(11)和(15)可知,无扰动时,PI控制系统能够无误差地跟踪时变输入,跟踪性能明显优于IP控制系统。对阶跃给定而言,其微分dv/dt为脉冲信号,幅值过大且时间较短,无法被系统响应,因此IDF近似不起作用。由式(14)和(18)可知,PI控制系统的阶跃响应必有超调,而IP控制系统的阶跃响应无超调,平稳性好。
接下来考虑系统的抗扰性能及抑制测量噪声性能。比较式(12)、(16)以及(13)、(17)可知,当PI控制和IP控制的系统带宽wn相同时(无论是否引入IDF),系统具有相同的抗扰性能和抑制测量噪声性能。
综上,IP控制系统虽然阶跃响应无超调,但对时变输入的跟踪性能变差。为此,本文提出一种兼顾PI控制和IP控制优点的控制策略,在不改变抗扰性能和抑制测量噪声性能的情况下,使系统在阶跃给定和时变输入时均有很好的跟踪性能。
3 转速环VSPI控制器
在图1所示的PI控制器的基础上,将误差比例环节与误差积分环节并联的结构改为误差的比例微分环节与积分环节串联的结构,得到的VSPI控制器框图如图4(a)所示。为方便比较,将图4(a)中误差的比例微分环节拆成输入与输出的比例微分环节之差,如图4(b)所示。相比于图3(b)所示的IP控制器,图4(b)所示的VSPI控制器增加了输入微分项kpssv(s)/kis。由图4可知,控制量为


图4 转速环VSPI控制器Fig.4 VSPI controller of speedloop
比较式(8)和(19)可知,VSPI控制器在本质上仍属于PI控制器。
3.1VSPI控制系统的跟踪性能
对于时变输入,IDF和输入微分项均可被系统响应,控制量如式(19)所示,此时VSPI控制和PI控制等效,无扰动时能够无误差地跟踪时变输入。
对于阶跃给定,其微分dv/dt为脉冲信号,电流环带宽有限、电流存在限幅等因素使得dv/dt无法被系统响应,IDF近似不作用。此外,起动瞬间,IDF使控制器饱和,抗积分饱和环节起作用,积分环节输入为0,之后输入微分项保持为0,因此,输入微分项在整个响应过程中都不起作用,此时VSPI控制与IP控制等效,响应无超调。
需要注意的是,实际系统一般为离散系统,阶跃给定时的脉冲信号dv/dt的幅值不是无穷大。当阶跃幅值v极低时,dv/dt的幅值较小。记离散系统的步长为Ts,vmin=bTsi*qmax,则v小于vmin时,dv/dt的幅值会低于电流限幅值,不足以在起动瞬间使控制器饱和,此时VSPI控制等效于PI控制,阶跃响应有超调,故本文所设计的VSPI控制器的阶跃给定幅值有下限vmin。
3.2VSPI控制系统的抗扰及抑制测量噪声性能
由式(12)和(16)可知,PI、IP、VSPI三种控制系统在扰动x2(s)作用下的传递函数相同。由式(13)和(17)可知,三种控制系统在测量噪声δns(s)作用下的传递函数也相同。由此可知,PI、IP、VSPI三种控制系统在系统带宽ωn相同时具有相同的抗扰性能和抑制测量噪声性能。
综上,VSPI控制可以在不改变系统抗扰性能和抑制测量噪声性能的情况下,既解决了阶跃响应的超调问题,又提高了对时变输入的跟踪性能。
4 实验验证
实验中所用的PMSM参数如表1所示。
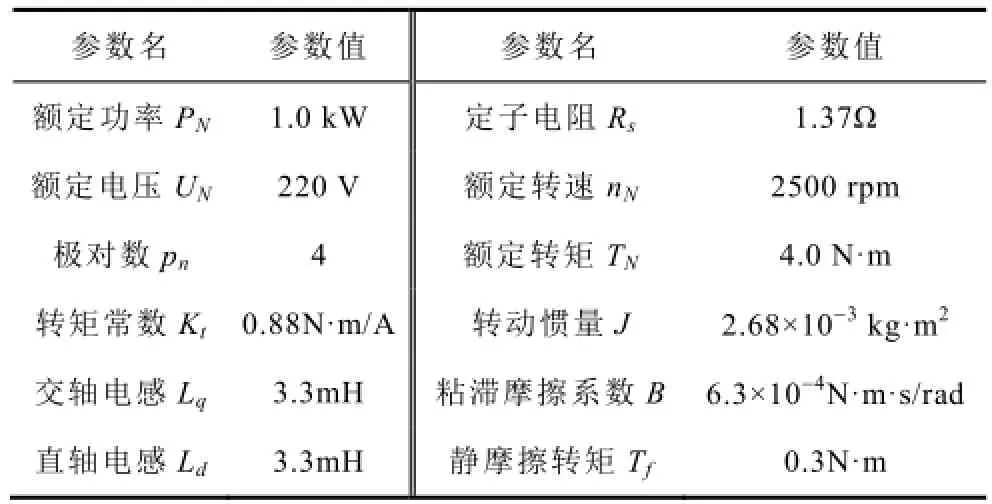
表1 电机参数Tab.1 Motor parameters
本实验平台永磁同步电机调速系统采用基于dSPACE实时仿真系统DS1103,利用快速原型法通过Simulink自动完成代码生成与下载。实验中的逆变器开关频率为10kHz,通过PWM中断触发电流采样和占空比更新。
速度环和电流环采样周期以及系统的计算步长均为0.1ms。两个电流环均采用PI控制,电流环带宽为2 000rad/s。电流限幅9A。经计算,阶跃幅值的下限值bTs为0.3rad/s,即2.8rpm。由于下限值极低,本文仅对下限值以上的阶跃给定展开分析。
接下来在PI、IP、VSPI三种控制系统的带宽一致的基础上验证VSPI控制器的有效性。如无特别说明,三种控制系统的带宽ωn均为80,即kps=2ωn= 160、kis=ωn2=6400。
4.1验证VSPI控制系统的跟踪性能
4.1.1 验证VSPI控制系统的阶跃响应
阶跃给定分别为80rpm和800rpm空载起动时的实验波形图如图5(a)、(b)所示。从图中可看出,VSPI和IP控制的动态响应完全相同,转速无超调,相比于PI控制,电流冲击要小,响应平稳性好。
对于VSPI控制系统,阶跃给定为800rpm空载起动,系统带宽ωn分别为80、160和320时的实验波形如图5(c)所示。由图5(c)可知,VSPI控制系统继承了IP控制系统的优点,随着ωn的增大,系统响应变快,跟踪性能越好。
4.1.2 验证VSPI控制系统对时变输入的跟踪性能
以正弦给定为例。给定500rpm/5Hz的正弦转速时的实验波形如图5(d)所示。由图5(d)可知,VSPI和PI控制的跟踪误差均为±5rpm,而IP控制的跟踪误差为±340rpm,VSPI和PI控制的转速响应完全相同,跟踪精度高,跟踪性能明显优于IP控制。由于实际电机即使空载也存在摩擦转矩、电流跟踪误差等扰动,故VSPI和PI控制对正弦给定的跟踪误差的实验值与理论值0稍有偏差,尽管如此,仍验证了理论分析的正确性。

图5 系统的跟踪响应波形与负载变化时的响应波形Fig.5 Waveforms of the system when tracking or load varing
4.2验证VSPI控制系统的抗扰性能
首先给定800rpm使电机空载稳定运行,而后测试加卸载对转速波动的影响。实验中所用测功机的加卸载曲线如图6所示,PI、VSPI和IP控制下的加卸载实验波形如图5(e)、(f)所示。图中三种控制的波形完全重合,验证了理论分析的正确性,即系统带宽相同时,三种控制的抗扰性能相同。

图6 实验负载曲线Fig.6 Load Curve in experiment
5 结论
本文针对系统的跟踪性能,在不牺牲抗扰性能和抑制测量噪声性能的基础上,提出了一种变结构PI控制器。利用输入微分前馈和遇限停止积分的抗积分饱和环节,使得系统对不同类型的转速给定自适应地呈现不同的结构特性。对于时变输入,VSPI控制等效于PI控制,无扰动时能够实现无误差跟踪;对于阶跃给定,VSPI控制等效于IP控制,阶跃响应无超调。需要注意的是,阶跃给定幅值不能低于下限值,否则将无法消除超调。实验结果验证了所提控制器的有效性和实用性,为研究高性能永磁同步电机调速系统提供了新方法。
[1] 王瑞萍, 皮佑国. 基于分数阶PI速度控制器的永磁同步电动机控制[J]. 电工技术学报, 2012, 27(11):69-75.
Wang Ruiping, Pi Youguo. Fractional-Order PI speed sontrollerfor permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 69-75.
[2] 梁骄雁, 胡育文, 鲁文其. 永磁交流伺服系统的抗扰动自适应控制[J]. 电工技术学报, 2011, 26(10):174-180.
Liang Jiaoyan, Hu Yuwen, Lu Wenqi. Anti-disturbance adaptive control of permanent magnet AC servo system [J]. Transactions of China Electrotechnical Society, 2011, 26(10): 174-180.
[3] 鲁文其, 胡育文, 梁骄雁, 等. 永磁同步电机伺服系统抗扰动自适应控制[J]. 中国电机工程学报, 2011, 31(03): 75-81.
Lu Wenqi, Hu Yuwen, Liang Jiaoyan, et al. Antidisturbance adaptive control for permanent magnet synchronous motor servo system[J]. Proceedings of the CSEE, 2011, 31(7): 75-81.
[4] 张洪帅, 王平, 韩邦成. 基于模糊PI模型参考自适应的高速永磁同步电机转子位置检测[J]. 中国电机工程学报, 2014, 34(12): 1889-1896.
Zhang Hongshuai, Wang Ping, Han Bangcheng. Rotor position measurement for high-speed permanent magnet synchronous motors based on fuzzy PI MRAS[J]. Proceedings of the CSEE, 2014, 34(12): 1889-1896.
[5] 黄佳佳, 周波, 李丹, 等. 滑模控制永磁同步电动机位置伺服系统抖振[J]. 电工技术学报, 2009, 24(11): 41-47.
Huang Jiajia, Zhou Bo, Li Dan, et al. Sliding mode control for permanent magnet synchronous motor servo system[J]. Transactions of China Electrotechnical Society, 2009, 24(11): 41-47.
[6] Shihua Li, Mingming Zhou, Xinghuo Yu. Design and implementation of terminal sliding mode control method for PMSM speed regulation system[J]. IEEE Transactions on industrial informatics, 2013, 9(4):1879-1891.
[7] 韩京清. 自抗扰控制技术—估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
[8] 黄科元, 周滔滔, 黄守道, 等. 永磁伺服系统基于微分自适应补偿的快速无超调控制策略[J]. 电工技术学报, 2014, 29(09): 137-144.
Huang Keyuan, Zhou Taotao, Huang Shoudao, Jiang Zhen, Ye Hongzhi. Non-Overshoot and fast response control of PMSM servo system based on differential adaptive compensation[J]. Transactions of China Electrotechnical Society, 2014, 29(09): 137-44.
[9] 郭新华, 温旭辉, 赵峰, 等. 基于电磁转矩反馈补偿的永磁同步电机新型IP速度控制器[J]. 中国电机工程学报, 2010, 30(27): 7-13.
Guo Xinhua, Wen Xuhui. A novel IP speed controller of PMSM based on electromagnet torque feedback compensation[J]. Proceedings of the CSEE, 2010, 30(27): 7-13.
[10] 王宏佳, 杨明, 牛里, 等. 永磁交流伺服系统速度控制器优化设计方法[J]. 电机与控制学报, 2012, 16(02): 25-31.
Wang Hongjia, Yang Ming, Niu Li, Xu Dianguo. Optimal speed controller design method forpermanent magnet AC servo system[J]. El ctri cmachines and control, 2012, 16(02): 25-31.
[11] 李光泉, 刘天翔, 等. 永磁同步电机调速系统的伪微分反馈控制[J]. 电工技术学报, 2010, 25(08):18-23.
Li Guangquan, Ge Hongjuan, Liu Tianxiang, et al. Pseudo derivative feedback control for PMSM drive system[J]. Transactions of China Electrotechnical Society, 2010, 25(08): 18-23.
[12] 杨明, 徐殿国, 贵献国. 控制系统Anti-Windup设计综述[J]. 电机与控制学报, 2006, (06): 16-20.
Yang Ming, Xu Dianguo, Gui Xianguo. Design review of anti-windup for control system[J]. Electric Machines and Control, 2006, (06): 16-20.
A Variable Structure PI Controller for Permanent Magnetic Synchronous Motor Speed-regulation System
Fu Hui Zuo Yuefei Liu Chuang Zhang Jie
(College of Automation Nanjing University of Aeronautics and Astronautics Nanjing 210016 Jiangsu China)
In permanent magnetic synchronous motor (PMSM) speed adjusting system, to conventional PI controller, overshoot of step response is hard to avoid. Although IP control can eliminate overshoot, response becomes slow, which leads to poor tracking performance. In this paper, a variable structure PI controller is proposed, which adopts input derivative feedforward (IDF) and changes the parallel structure between error proportion and error integral into the cascaded structure between error proportion and integral based on conventional PI controller.With stop integrating at limit, VSPI controller is equal to PI controller for time-varying input and equal to IP controller for step input, thus overshoot is eliminated and tracking accuracy is high. Extensive experiments are performed to verify the validity and practicality of the proposed controller.
permanent magnetic synchronous motor, PI, IP, overshoot, input derivative feedforward
TM351
符 慧 女,1992年生,硕士研究生,研究方向为永磁同步电机伺服系统控制。
国家自然科学基金(51377076),江苏省“六大人才高峰”资助项目(YPC13013),江苏省产学研资金(BY2014003-09)。
2014-09-10
左月飞 男,1989年生,博士研究生,研究方向为永磁同步电机伺服系统控制。

