基于连续型定子磁链轨迹的异步牵引电机低转矩脉动控制算法

范文进-Pham Van Tien 郑琼林 杨中平 林 飞宋文胜 Do Viet Dung

基于连续型定子磁链轨迹的异步牵引电机低转矩脉动控制算法

范文进-Pham Van Tien1郑琼林1杨中平1林 飞1宋文胜2Do Viet Dung3

（1. 北京交通大学电气工程学院 北京市 海淀区 100044 2. 西南交通大学电气工程学院 四川省 成都市 610031 3. 交通运输大学机械系 河内市 越南）

本文提出了一种定子磁链轨迹优化的异步牵引电机基速以内的中高速区直接转矩控制(Direct Torque Control, DTC)算法。所提出DTC算法是从以改善转矩脉动角度出发，牵引电机在基速以内的中高速度运行阶段时，随着转速的增加，通过实现定子磁链轨迹从圆形-多边形-六边形的连续切换，获得转矩脉动小与平稳，磁链轨迹平滑、开关频率利用率以及谐波消除能力等的提高。该DTC算法仅需在传统DTC基础结构上仅增加定子磁链调节算法即可，因此它的主要优点是算法简单性，并保留了传统DTC算法快速动态响应，控制电路不复杂，对电机参数依赖性低等特征。理论分析和实验结果都证明了该连续型磁链轨迹的DTC算法的有效性和可行性。

直接转矩控制 异步牵引电机 减小转矩脉动 优化磁链轨迹 基速

1 引言

传统直接转矩控制（DTC）存在转矩波动大，开关频率不固定和定子电流谐波大等缺点[1]。一个比较有效的解决方案是采用空间矢量调制直接转矩控制（DTC-SVM）算法[2]。近年来在提出改进传统DTC的算法中，DTC-SVM算法继续受到重视[3-4]。但这种改进算法削弱了传统DTC结构简单的特性[5]，在基速以内的中高速段的大功率，低开关频率场合传统DTC算法显示更加优异的性能[6]。

自从直DTC理论诞生以来，根据磁链轨迹不同，到目前已经有了基于圆形磁链轨迹[7]，三十边形磁链轨迹[6,8]，十八边形磁链轨迹[9]，以及六边形磁链轨迹[10]的四种传统DTC算法被提出。传统DTC算法中，逆变器的开关频率与开关次数随着转矩调节器的容差、磁链调节器的容差、以及电机速度变化而变化[11-13]。其中开关频率与开关次数反比于转矩和磁链调节器的容差，而正比于电机速度。其转矩和磁链调节器的容差越小，相应的开关频率与开关次数越大；其电机速度越大，开关频率与开关次数越大。另外，定子电流谐波含量与转矩和磁链调节器的容差呈正比关系[11,13]。因此在同样其他的控制条件下，上述控制算法中圆形磁链轨迹DTC算法具有磁链调节器的容差最小则开关频率与开关次数最大，但定子电流谐波含量最小，而六边形磁链轨DTC算法迹恰好相反。

由于大功率牵引变流器开关频率低的限制[14-16]，因此异步牵引电机采用DTC算法在基速度范围必须采用不同磁链轨迹控制模式[17,18]。为了提高了开关频率的利用率，改善定子电流的正弦度，文献[6，8]将现有异步牵引电动机DTC全速范围定子磁链轨迹扩展为:圆形-＞三十边形-＞十八边形-＞六边形的多磁链轨迹控制模式。但在开关频率允许情况下，为了进一步减小定子电流谐波，要实现更多边形的磁链轨迹，显然这种多边形磁链轨迹设计与实现方法都比较复杂。

针对异步牵引电机采用DTC算法的特点，当开关频率允许情况下，以减小与平稳转矩脉动，磁链轨迹更佳平滑，提高开关频率以及谐波消除能力为目标，提出一种简单而有效的基于连续型磁链轨迹的异步牵引电机DTC算法。该算法将基速以内定子磁链轨迹控制模式扩展为:圆形模式至多边形模式，最后到六边形模式。本文首先简单的描述DTC技术的基本原理；然后以传统圆形磁链轨迹DTC算法，进行分析传统制定电压矢量表的依据对磁链速度以及转矩的影响，在此基础上，详细分析和讨论了基于连续型定子磁链轨迹的异步牵引电机基速以内的中高速度运行阶段DTC算法；最后，对所提出的DTC算法进行了实验验证。

2 异步牵引电机基速以内的中高速度段DTC算法

2.1DTC基本原理

DTC技术基本原理已经很成熟，因此这里只简短的描述其基本原则以便于读者容易理解本文后面所提出的控制算法。

根据异步电机的数学模型，定子磁链和电磁转矩在定子静止坐标系上由下列空间矢量方程式表示:

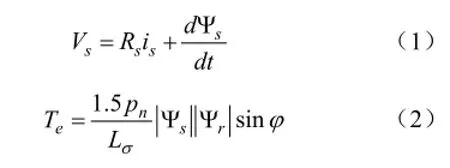
其中Vs是定子电压空间矢量；Rs是单相定子电阻；is是定子电流空间矢量，Ψs，Ψr是定子，转子磁链空间矢量；Te是电磁转矩；pn是极对数；Lσ是单相转子漏感与定子漏感之和；φ是磁通角，即定子磁链与转子磁链之间的夹角。

式（1）表明，若忽略在定子电阻上的压降Rsis，当输入电压为一个非零电压的综合矢量时，定子磁链的矢量Ψs将沿着输入电压综合矢量的方向，以正比于输入电压值的速度（即该电压作用时间）移动。磁链变化量|ΔΨs|=VsΔt。

式（2）表明，在动态控制中，只要控制的响应时间比转子时间常数小，这样在短暂的过程中就可以认为转子磁链不变，这时只要维持定子磁链的幅值恒定不变，通过改变磁通角就可以迅速地控制转矩。在DTC中，其基本控制方法就是通过空间电压矢量VS来控制定子磁链的旋转速度，控制定子磁链走走停停，以改变定子磁链的平均旋转速度的大小，从而改变磁通角的大小，以达到控制电动机转矩的目的。

电机采用DTC技术，是通过控制电磁转矩和定子磁链来完成电机调速目的。下面在两电平电压源型逆变器供电情况下，对六边形磁链轨迹和圆形磁链轨迹两种控制模式对转矩和定子磁链的控制进行简单的描述。

在基于六边形磁链轨迹DTC系统中，其基本控制框图如图1所示，定子磁链的控制由定子磁链滞环控制器控制六个非零电压矢量来完成定子六边形磁链轨迹。转矩滞环控制器控制两个零矢量与磁链环的六个非零电压矢量之间的转换以控制转矩，其中前者的作用是减小转矩，而后者的作用是加大转矩。图2是定子六边形磁链轨迹与电压矢量在定子静止坐标系上的分布情况。

图1 六边形磁链轨迹DTC的系统控制框图Fig.1 Block diagram of DTC with hexagon

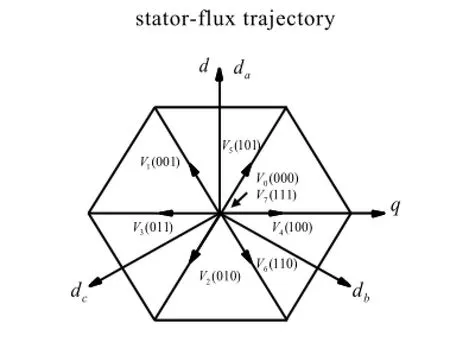
图2 六边形磁链轨迹与电压矢量的分布Fig.2 Hexagon stator-flux trajectory and space voltage vector

图3 为基于圆形磁链轨迹DTC系统的基本控制框图。该控制算法采用了查询电压矢量表的方法来对定子磁链和电机转矩同时进行调节。其首先将圆形空间分成六个扇区θ(i)（i=1～6），如图4所示，然后根据定子磁链滞环控制器，转矩滞环控制器以及当前定子磁链矢量所在的扇区的三个信号来制定电压矢量表。在Takahashi和Noguchi首先提出的DTC系统中[7]，转矩滞环控制器采用三点式型，以采用反向电压矢量与零电压矢量的两种电压矢量来减小转矩要求。因牵引逆变器有低开关频率的要求，且在电机中高速度段反向电压矢量会使转矩下降的较快，导致更大的转矩波动。所以，本文采用两点式型来代替三点式转矩型滞环控制器，这样电压矢量表1以电机顺时针旋转来制定就会避免出现反向电压矢量带来的副作用。

图3 圆形磁链轨迹DTC的系统控制框图Fig.3 Block diagram of DTC with circle stator-flux

图4 圆形磁链轨迹与磁链扇区Fig.4 Circular stator-flux trajectory and stator flux sector

表1 顺时针旋转的空间电压矢量查询表Tab.1 Voltage vector selection table in the case of clockwise rotation

DTC理论中，转矩控制是通过控制定子与转子磁链之间的夹角φ来完成的，传统的方法是通过电压矢量与定子磁链矢量之间的方向来选择电压矢量，即选择能使定子磁链矢量向前旋转的电压矢量来使转矩增加。下面以定子磁链矢量在θ（1）扇区为例，来分析用以上方法去制定电压矢量表在基速以内的中高速度段对磁链速度与转矩的影响，如图5所示。

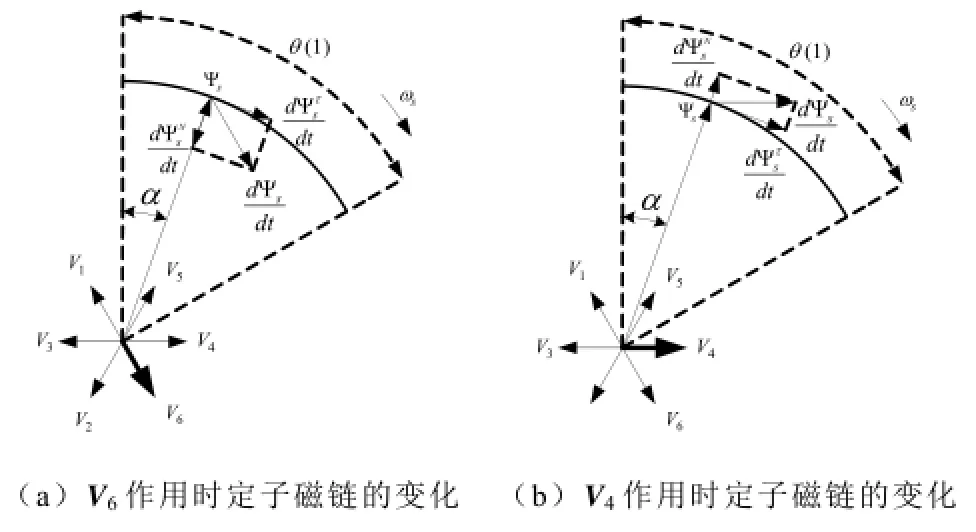
图5 电压矢量对定子磁链的影响Fig.5 Influence of voltage vector on stator flux

2.2传统制定电压矢量表的方法对磁链速度的影响

先考虑控制组（CT=1, CΨ=0），相当于这时需要增加转矩和减小磁链，则V6被选择。在中高速度段可以忽略定子电阻压降，则式（1）改写成:

因为非零电压矢量的幅值都等于2/3Vdc所以（3）变为:

从图5（a）可算出定子磁链矢量切向与法向分量分别由下面两式来表示:

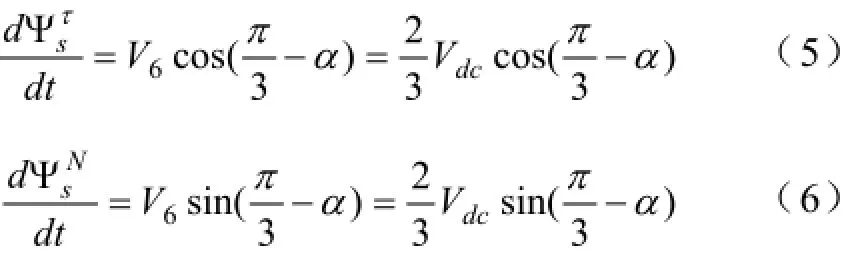
可知，定子磁链矢量法向分量表示磁链值的变化量，而定子磁链矢量切向分量表示磁链切线速度，则定子磁链瞬时角速度由下式计算:

其中（0≤α≤π/3）

式（7）表明，定子磁链瞬时角速度跟α是正比关系，当（0≤α≤π/3），则ω2≤ωs≤ω1，其中ω1和ω2由一下两式所示:

再考虑控制组（CT=1, CΨ=1），相当于需要同时增加转矩和磁链，则V4被选择。这时定子磁链瞬时角速度写成:

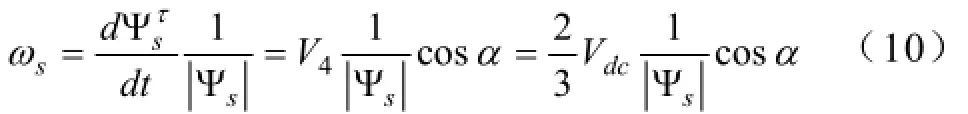
式（10）表明，α与定子磁链瞬时角速度呈反比关系，当（0≤α≤π/3）时，（ω1≥ωs≥ω2）。从式（7）和式（10）可看出，在扇区θ（1），电压矢量V6和V4对定子磁链瞬时角速度的影响是相反的。

2.3基速以内的中高速度运行阶段传统制定电压矢量表的方法对转矩的影响

式（2）可改写成:

其中ωr是转子瞬时电角速度。

式（11）表明，如需要加大转矩则得使sin[(ωsωr)t]＞0，即ωs＞ωr。

在扇区θ（1），由电压矢量V6来实现控制组（CT=1, CΨ=0）。当转子瞬时电角速度ωr＞ω2时，在该扇区存在一个分区，即（0≤α＜β）分区，其中β表示在电压矢量V6的作用下定子磁链与当前转子瞬时电角速度相等的定子磁链矢量当前在扇区θ（1）的位置，且（0＜β＜π/6）。由上节分析可知，当定子磁链矢量的位置在这分区里时，当前转子瞬时电角速度大于定子磁链瞬时角速度，即ωs＜ωr。这表示，V6的作用只能满足磁链控制要求，它虽然可使定子磁链矢量向前旋转，但已经不能使转矩曾加，不满足转矩控制要求。

同样，在扇区θ（1）由电压矢量V4来实现控制组（CT=1, CΨ=1）。当转子瞬时电角速度ωr＞ω2时，在扇区θ（1）里又存在一个分区，即（π/3-β≤α＜π/3）分区，其中（π/3-β）表示在电压矢量V4的作用下定子磁链与当前转子瞬时电角速度相等的定子磁链矢量当前在扇区θ（1）的位置。当定子磁链矢量的位置在这分区里时，当前转子瞬时电角速度大于定子磁链瞬时角速度，即ωs＜ωr。跟上述的V6的结果一样，即这里V4的作用只能满足磁链控制要求，它虽然可使定子磁链矢量向前旋转，但已经不能够使转矩曾加，不满足转矩控制要求。

上述说明，当ωr＞ω2时，定子磁链的每个扇区都存在两个分区，即（0≤α＜β）与（π/3-β≤α＜π/3）分区。当定子磁链矢量的位置在这两个分区里，根据传统电压矢量表的制定方式，即按电压矢量与定子磁链矢量之间的方向来制定电压矢量表，则只能实现定子磁链控制要求，而不能实现转矩控制要求，所以转矩出现失控现象。这两个分区叫为转矩失控分区，如图6所示。电机转速越高，这两个转矩失控分区越宽，转矩波动越大与越不平稳。

图6 转矩失控分区Fig.6 Lost torque control sub-sector

2.4提出异步牵引电机基速以内的中高速度段的DTC算法

当转速ωr＞ω2时，为了解决上述问题，可以通过改变定子磁链轨迹以排除转矩局部失控分区，即以能使磁链旋转更快的电压矢量来代替不能使磁链旋转速度达到要求的电压矢量。根据目前已提出的四种磁链轨迹控制模式，可形成从圆形到三十边形，接着十八边形最后达到六边形磁链轨迹控制的控制过程。但是这个方案从磁链轨迹平滑性，开关频率利用率，谐波消除能力等多性能指标还不够理想。因此在开关频率允许的情况下，为了有更好的效果，本文提出一种连续多磁链控制模式，它的实现如图7所示。

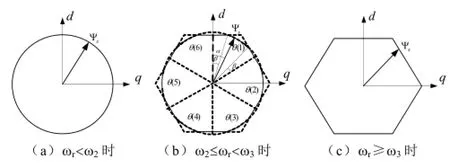
图7 各速度段的定子磁链轨迹Fig.7 Stator-flux trajectory in speed ranges

因为对称性，下面以扇区θ（1）为例进行说明整个控制过程。

由上述可知，当转子速度ωr＜ω2时，因为还没有出现转矩局部失控分区，所以系统在圆形磁链轨迹控制模式下工作，因此磁链轨迹如图7a所示。

当转子速度ωr＞ω2时，由上述分析可知，在扇区θ（1）里有两个转矩局部失控分区出现，其电压矢量V6对转矩失控的分区（0≤α＜β）和电压矢量V4对转矩失控的分区（π/3-β≤α＜π/3）。如果在（0≤α＜β）分区以V4代替V6，而在（π/3-β≤α＜ π/3）分区以V6代替V4。这样就消除了这两个转矩失控分区。因此磁链轨迹如图7b所示。

随着电机速度的增加，β也加大，磁链轨迹从圆形连续平滑地过度到更少多边形，直到ωr=ω3，也即β=π/6时达到六边形，其中ω3由式（12）表示。之后系统工作在六边形磁链轨迹控制模式，其如图7c所示。

其中Ψsref是圆形磁链轨迹控制模式下的磁链给定值。

在过度阶段，扇区θ（1）的（0≤α＜β）与（π/3-β≤α＜π/3）的两个分区磁链轨迹分别由V4和V6来完成，剩下的分区磁链轨迹由V6与V4共同来实现。从圆形磁链轨迹与六边形磁链轨迹的实现方法可以看到，只要在（0≤α＜β）和（π/3-β≤α＜π/3）的两个分区，使系统在六边形磁链轨迹控制模式下工作，而在转矩非失控分区（β≤α＜π/3-β）使系统工作在圆形磁链轨迹控制模式，由此可实现上述消除转矩失控的设计方法。图7为提出控制算法的系统控制框图。

从图1所示六边形磁链轨迹DTC框图与图3所示圆形磁链轨迹DTC框图可以看出，新提出控制算法的系统控制框图由这两者再增加三个模块所构成。这三个模块包括:1）“β计算”模块，其作用是确定圆形控制模式下的转矩失控与非失控分区；2）“α与β比较”模块，其作用是判断定子磁链当前位置所在的分区以确定两者的切换时刻；3）圆形控制模式下的“磁链参考值估算”模块，其作用是实现两者的平滑过渡。

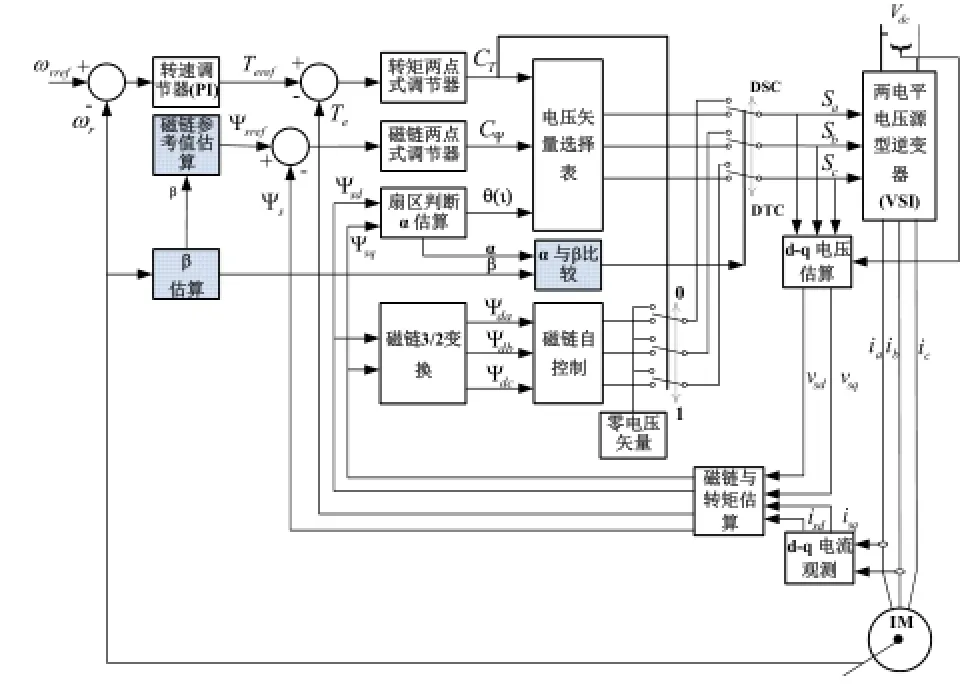
图8 连续多磁链控制模式DTC的系统控制框图Fig.8 Structure of DTC with continuous stator-flux linkage locus

3 实验结果

本文采用实验室的小功率异步电动机进行原理验证。具体电机参数为:额定功率PN=5.5（kW），额定电压VN=380（V），额定转矩TN=35（Nm），额定转速ωN=1 450（r/min），定子电阻Rs=1.517（Ω），定子漏电感Lls=2（mH），转子电阻Rr=1.483（Ω），转子漏电感Llr=2（mH），互感Lm=172（mH），极对数np=2，转动惯量j=0.83（kg.m2）。

因为在空载情况下进行做实验，考虑到安全问题与结果的精细度而给出的实验参数如表2所示。

表2 实验参数Tab.2 Experiment parameters

从实验参数算出（0～200 rad/s）是电机基速范围，ω1=200rad/s，ω2=100rad/s和ω3=150rad/s。因此，在本文提出的连续多磁链控制模式中，当转子速度小于100rad/s时，系统工作在圆形磁链轨迹控制模式；当转子速度大于等于100rad/s 而小于150rad/s时，系统工作在过渡过程；当转速大于等于150rad/s时，系统进入六边形磁链轨迹控制模式工作。基速以内的各速度分段与对应的控制模式如图9显示。为了便于区分，令基于传统圆形磁链轨迹的DTC算法为DTC1，所提出的连续多磁链轨迹DTC算法为DTC2。

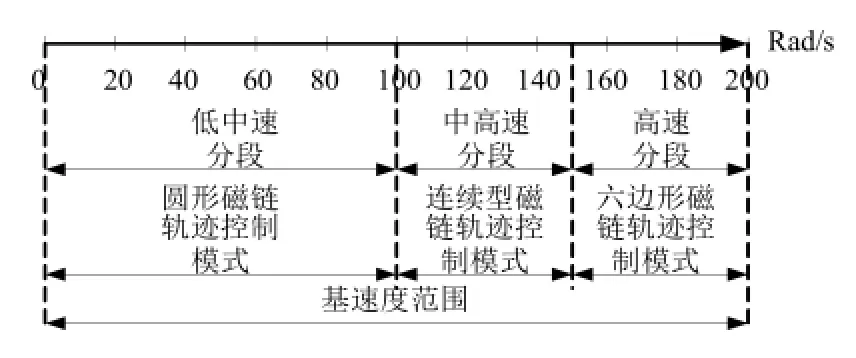
图9 基速以内的各速度段与相应的控制模式Fig.9 Work of the proposed DTC system with a range（0～200 rad/s）of basic speed

图10 显示当转子速度从0增加至160rad/s时DTC2的定子磁链幅值与图11显示电机速度在100～150rad/s的过度速度段某个转子速度的磁链轨迹的实验结果。从实验结果可以看出，过渡过程中，随着电机速度增加，定子磁链幅值也逐渐地曾加，定子磁链轨迹依次平滑地从圆形、多边形及六边形连续与平稳的切换，对每个速度都有相当而尺寸不同的多边形磁链轨迹。因此获得了磁链轨迹平滑、开关频率利用率以及谐波消除能力等的提高[6, 8]。

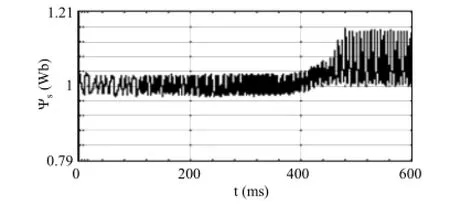
图10 ωr=0～160rad/s时DTC2的定子磁链幅值Fig.10 Stator flux amplitude of DTC2 with ωr=0～160rad/s

图11 过度阶段某个转子速度DCT2的定子磁链轨迹Fig.11 Stator-flux trajectory of DTC2 with different rotor speeds

图12 显示DTC1在三种转子速度变化范围的转矩波形，分别为0～90rad/s，0～140rad/s和0～160rad/s。图12a显示当转子速度从0增加至90rad/s时的转矩波形。此转速段为基速以内的低中速分段。在该速度段因为还未出现转矩失控现象，所以转矩波形的波动比较均匀。从图中还可以看到在整个速度段转矩的正与负脉动有所改变，随着速度的增加正转矩脉动减小而负转矩脉动增加。这种现象的原因由于随着转速的增加，非零电压矢量对转矩上升率的影响减小，而零电压矢量对转矩减小率的影响增大所造成的。显然这是传统DTC算法本身控制性能的特点。另外，虽然给定转矩调节器的容差等于5% Teref，但是由于传统DTC算法中在一个开关周期内只输出一个电压矢量结合离散控制的特点，所以实际转矩脉动总是超过给定容差。

图12 各转子速度段DTC1的转矩波形Fig.12 Torque curve of DTC1 in rotor speed ranges

图12 b和12c分别显示在两种转子速度变化范围为0～140rad/s和0～160rad/s DTC1的转矩波形。由图12b可知，转矩波形在中高速度段出现负的突变波动。在该速度分段的末端，平稳负波动在-1.2Nm左右，但突变负波动为-2.6Nm左右；在图12c中的末端，平稳负波动在-1.6Nm左右，而突变负波动已降低至-3.95 Nm左右。可以看出转子速度越大，波动越大，即转矩失控现象越厉害。具体的转矩失控位置可由图13看出。

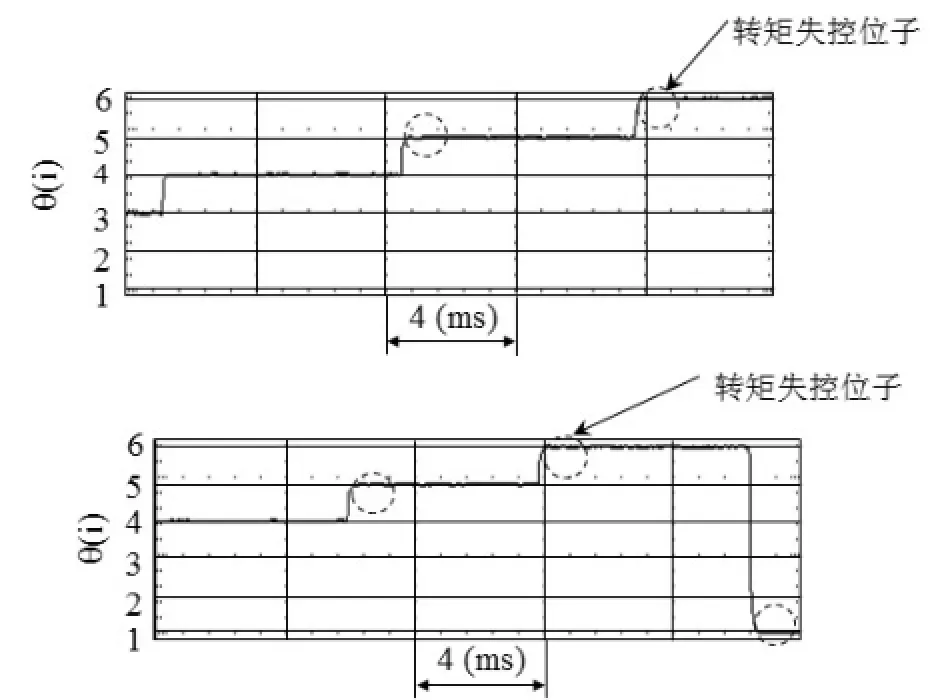
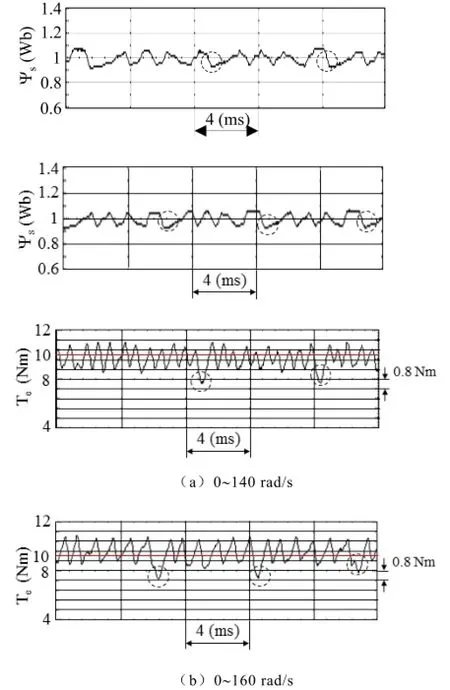
图13 各转子速度段末端DTC1的磁链扇区，磁链幅值与转矩的放大波形Fig.13 Experiment results of stator flux sector, stator flux amplitude and torque using the DTC1 in a large scale

图13 表示当转子速度变化范围分别为0～140 rad/s，图13a和0～160rad/s，图13b的磁链扇区，磁链幅值与转矩在末端处的放大波形和相应的转矩失控位置。从上面转矩局部失控现象分析可知，转矩负突变的位置应在扇区两侧。但从式（11）看出，转矩总的变化趋势应该由定子磁链值和定子磁链与转子磁链之间的夹角所确定。所以在扇区末段，虽然磁链夹角减小，但被定子磁链增加来拟补，使得转矩在一定的中速度范围内还能缓慢增加。而在初始段由于磁链夹角减小再加上磁链同时的减小，使得转矩负突变更加厉害。

图14分别显示在两种转子速度变化范围为0～140 rad/s和0～160 rad/s DTC2的转矩波形。从实验结果可知，新的控制算法克服了转矩局部失控现象，转矩波形几乎没有出现负的突变波动，只有跟DTC1相同的平稳波动，转矩的脉动比较均匀，克服了DTC1算法存在的问题。

图14 DTC2模式下各转子速度段的转矩波形Fig.14 Torque curve of DTC2 in rotor speed ranges

另一方面，结合图10和图14可看出，在磁链过度过程中，转矩波形中也没有出现突变的波动，验证了DTC2的有效性与可行性。

4 结论

本文提出一种简单而有效的异步牵引电机中高速度运行阶段的直接转矩控制算法。在这种控制方式中，通过分析传统所制电压矢量表的依据对磁链速度以及转矩的影响。在此基础上，重点介绍了电机在基速度以内的中高速度运行阶段时，从以改善转矩转矩脉动角度出发，通过改变定子磁链轨迹的思想，实现定子磁链轨迹从圆形-多边形-六边形的连续切换。获得了磁链轨迹平滑，转矩脉动小与平稳。所提出的算法保留了传统DTC算法的原有优点[19]，因为它仅需在传统DTC结构中增加调节定子磁链算法。理论分析与实验结果表明所提出的方法简单有效。

该算法具有灵活性较高，在具体应用情况下可同时考虑转矩脉动与开关频率要求来调整模型的切换时刻，但还保留着连续与平滑的磁链轨迹。

[1] Buja G, Kazmierkowski M. Direct torque control of PWM inverter-fed AC motors—a survey[J]. IEEE Transactions on Industry Applications, 2004, 51(4)：744-757.

[2] Hableter T G, Profumo F，Pastorelli M，et al．Direct torque control of induction machines using space vector modulation[J]. IEEE Transactions on Industry Applications, 1992, 28(5)： 1045-1053．

[3] 宋文胜，冯晓云，侯黎明，葛兴来.电力牵引传动系统的三电平直接转矩控制算法的半实物实验研究[J]. 电工技术学报, 2012, 27(2)： 165-172.

Song Wensheng, Feng Xiaoyun, Hou Liming, Ge Xinglai. Hardware-in-loop research of three-level direct torque control scheme for electric traction drive system[J]. Transactions of China Electrotechnical Society, 2012, 27(2)： 165-172.

[4] 邱鑫，黄文新，杨建飞，卜飞飞. 一种基于转矩角的永磁同步电机直接转矩控制[J]. 电工技术学报, 2013, 28(3)： 56-62.

Qiu Xin, Huang Wenxin, Yang Jianfei, Bu Feifei. A direct torque control strategy based on torque angle for permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2013, 28(3)：56-62.

[5] 牛峰，李奎，王尧. 基于占空比调制的永磁同步电机直接转矩控制[J]. 电工技术学报, 2014, 29(11)：20-29.

Niu Feng, Li Kui, Wang Yao. Model predictive direct torque control for permanent magnet synchronous machines based on duty ratio modulation[J]. Transactions of China Electrotechnical Society, 2014, 29(11)：20-29.

[6] 廖永衡. 电力牵引传动系统直接转矩控制若干关键问题研究[M]. 成都： 西南交通大学, 2013.

[7] Takahashi I and Noguchi T. A new quick-response and high efficiency control strategy of an induction motor[J]. IEEE Transactions on Industry Applications, 1986, 22(5)： 820-827.

[8] 廖永衡，冯晓云，王珍. 低开关频率下基于直接自控制的谐波抑制方法[J]. 电工技术学报, 2012, 27(8)： 126-132.

Liao Yongheng, Feng Xiaoyun, Wang Zhen. Research on harmonic elimination in low switching frequency based on direct self control[J]. Transactions of China Electrotechnical Society, 2012, 27(8)： 126-132.

[9] Steimel A. Further development of direct self control for application in electric traction[C]. Proceedings of the IEEE International Symposium on Industrial Electronics, Warsaw, Poland, 1996： 180-185.

[10] M. Depenbrock. Direct self control (DSC) of Inverter Fed Induction Machine[J]. IEEE Transactions on Power Electronics, 1988, 3(4)： 420-429.

[11] Casadei D, Grandi D, Serra G, Tani A. Effects of Flux and Torque Hysteresis Band Amplitude in Direct Torque Control of Induction Machines[C]. In Pro. IEEE IECON'94, Bologna, 1994.

[12] Kazmierkowski M P, Kasprowicz A B. Improved direct torque and flux vector control of PWM inverterfed induction motor drives[J]. IEEE Transactions On Industrial Electronics, 1995, 42(4)： 344-349.

[13] Kang Jun-Koo, Sul Seung-Ki. Analysis and prediction of inverter switching frequency in direct torque control of induction machine based on hysteresis bands and machine parameters[J]. IEEE Transactions On Industrial Electronics, 2001, 48(3)： 545-553.

[14] M. Depenbrock. Direct self control (DSC) of Inverter Fed Induction Machine[J]. IEEE Transactions on Power Electronics, 1988, 3(4)： 420-429.

[15] Baader U, Depenbrock M, Gierse G. Direct self control (DSC) of inverter fed induction machine： A basis for speed control without speed measuremen[J]. IEEE Transactions on Industrial Applications, 1992, 28(3)： 581-588.

[16] 周明磊，游小杰，王琛琛. 电力机车牵引传动系统矢量控制[J]. 电工技术学报, 2011, 26(9)： 110-115，129.

Zhou Minglei, You Xiaojie, Wang Chenchen. Vector control of driving system of locomotive[J]. Transactions of China Electrotechnical Society, 2011, 26(9)：110-115, 129.

[17] 冯晓云. 电力牵引交流传动及其控制系统[M]. 北京： 高等教育出版社, 2009.

[18] Steimel A. Direct self control and synchronous pulse techniques for high-power traction inverters in comparison[J]. IEEE Transactions on Industrial Electronics, 2004, 51(4)： 810-820.

[19] 宋文胜，冯晓云. 电力牵引交流传动控制与调制技术[M]. 北京： 科学出版社, 2014.

A low torque ripple control scheme of asynchronous traction motor with continuous stator-flux linkage locus

Tien Van Pham1 Trillion Q. Zheng1 Yang Zhongping1 Fei Lin1 Song Wensheng2 Dung Viet Do3
（1. School of Electrical Engineering Beijing Jiaotong University Beijing 100044 China 2. School of Electrical Engineering Southwest Jiaotong University Chengdu 610031 China 3. Department of Mechanical Engineering University of Transport and Communications Hanoi Vietnam）

A direct torque control(DTC) of asynchronous traction motor with the optimal stator flux-linkage locus is proposed to apply in medium and high speed ranges. In order to reduce torque ripple, the stator flux-linkage track of the proposed DTC can be switched continually from roundness to polygon to hexagon with the increase of rotor speed; hence, it can obtain smoothly stator flux, high utilization switching frequency and good harmonic elimination ability. The proposed DTC method can be realized by adding stator flux-linkage regulation in traditional DTC control structure, whose advantages are its simplification, and retention of traditional DTC’s features such as fast dynamic response, simple control structure, and low dependence on motor parameters. Theory analysis and experimental results both demonstrate the effectiveness and feasibility of the proposed DTC method with continuous flux-linkage locus.

Direct torque control, asynchronous traction motor, torque ripple decreasing, flux-linkage track optimization, the base speed

TM351

Pham Van Tien-范文进 男，1981年生，博士生，研究方向为轨道交通电力牵引传动技术。

2014-09-10

郑琼林，男，1964年生，教授，博士生导师，研究方向为轨道交通牵引供电与交流传动，高性能低损耗电力电子系统，光伏发电并网与控制，电力有源滤波与电能质量。