一种新型混合储能拓扑及其功率分流算法

常丰祺 郑泽东 李永东

一种新型混合储能拓扑及其功率分流算法

常丰祺 郑泽东 李永东

（清华大学电机系电力电子与电机控制研究室 北京 100084）

拓扑结构和功率分流算法是混合储能系统研究的两个重要内容。本文提出了一种基于模块化级联多电平拓扑的混合储能变换器，并且采用了一种特殊的载波层叠调试方法实现模块间的电压均衡。针对混合储能中的功率分流控制问题，本文总结了最经常采用的低通滤波器法的缺点，并在仿真和实验中与一种新的功率分流算法进行了对比。本文在MATLABSIMULINK平台上进行了仿真研究，得到了仿真结果，并且在小容量实验平台获得了短时间运行和长时间运行的实验结果。

功率分流 混合储能 主动均衡 模块化多电平拓扑

1 引言

近年来，随着风能、太阳能等新能源发电不断发展起来，装机容量越来越大，但是其不确定性会对电网造成很大影响。国内外研究表明，若风电装机容量占总容量的比例超过20%，将严重影响电网的调峰能力和安全运行[1]。为确保高可靠性、高质量供电，储能装置联网应用具有加大发展前景。储能模块可以集成在“发—输—配—用”等各个环节中，在负荷低谷时作为负荷从电网中吸收多余能量并存储起来，待电力不足或负荷高峰时再将存储的能量释放出来以供使用，为电力系统“削峰填谷”。如此不仅可以提高电力系统的稳定性，并且能够帮助电力系统经济调度，从而提高能源利用率、降低环境污染[2,3]。

由于单一储能介质组成的储能装置性能会受到这种储能介质特性的限制，所以在实际中混合储能系统应用的越来越多。由于混合储能系统涉及多种储能介质，因此其拓扑设计和功率分流算法都是重要的研究内容。

拓扑方面，传统的思路是将储能装置直接串并联后，通过DC/DC变换器或者直接连接在直流母线上，然后再采用DC/AC变换器并网输出。文献[4-10]都采用了此类拓扑。这类拓扑的优点是结构和控制简单，但是当串并联数比较大时，单个储能模块损坏即需要停机维修，而且必须给系统附加专门的电池均衡电路[11]。文献[10,12]提出的能量均衡电路就是用来应对此种情况。文献[10]中的均衡电路需要专门的控制器来控制均衡过程。这导致系统结构复杂，模块化变差。文献[12]中提出的均衡器虽然成本较低，但均衡的过程中有能量损失，最高效率仅为90%。解决能量均衡问题的一种思路是前文所述的附加专门的均衡电路，另一种思路是改良拓扑，使拓扑本身就具有主动能量均衡能力。模块化多电平拓扑就具有这种特点[13-14]。它可以利用轮换充放电的方式解决不均衡问题，不需要附加额外的均衡装置，均衡过程本身没有能量损失，同时电路的模块化程度也会提高。本文研究的新型混合储能拓扑就是基于MMC拓扑提出的。

功率分流算法方面，研究是功率分流算法是为了提高储能系统的性能，使多种储能介质的优点都能尽可能体现。文献[3,4,15]使用低通滤波器将功率指令中的低频分量提取出来作为电池的功率指令而高频部分则由超级电容产生。但是这种方法名没有考虑超级电容的SOC和电池的功率上限，因此某些特定的工况下会导致电容或电池损坏。文献[4]采用了低通滤波器法的改进型方法，为电池功率增加了限幅，但也未考虑超级电容的SOC状态。文献[5]提出了一套功率分流的决策机制，只要超级电容电压在安全范围内，则蓄电池不参与充放电，但超级电容达到极限电压后，蓄电池必须承担高频功率。文献[16]则是通过查询一条电池电流-超级电容电流曲线来确定功率分流比，但这种方法没有考虑两种储能介质的频率特性，因此可能对电池的寿命造成影响。

本文提出了一种基于MMC拓扑的新型混合储能电路，使用超级电容和电池作为储能介质，并提出了相应的调制方法，可以在PWM调制过程中实现蓄电池和超级电容的主动电压均衡。在此拓扑基础上，将传统的低通滤波器法和一种新型功率分流算法进行了对比。本文使用SIMULINK平台上对拓扑和功率分流算法进行了仿真，并搭建了一个小容量实验系统，得到了实验结果。

2 新拓扑及其PWM调制方法

2.1拓扑介绍

基于MMC的新型混合储能拓扑如图1所示。

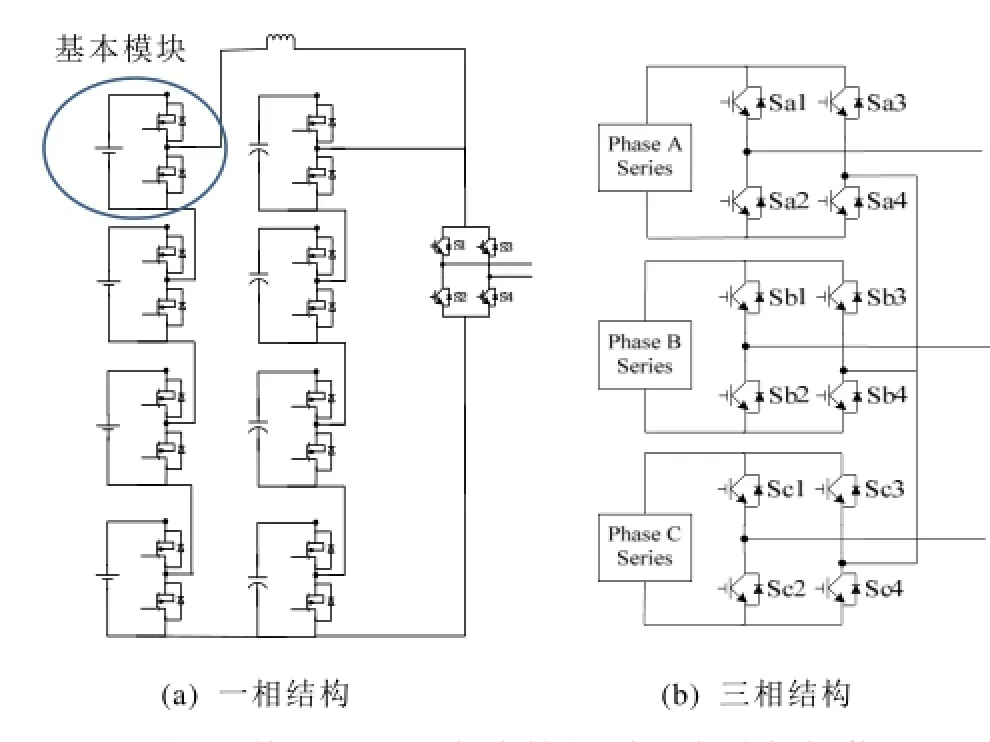
图1 基于MMC电路的新型混合储能拓扑Fig.1 Novel hybrid energy storage topology based on MMC

拓扑的基本模块为连接有电池或超级电容储能模块的半桥变换器，如图1a圈中所示。当半桥变换器的上管开通下管关断时，输出储能模块的端电压；当下管开通上管关断时，储能模块被旁路，半桥输出零。基本模块构级联成蓄电池支路和超级电容支路，超级电容支路直接连接在H桥的直流母线上，而电池支路通过一个电感连接在直流母线上，两个支路的级联数相等。根据交流参考电压，超级电容支路在直流母线上输出多电平直流电压，再经过H桥换向变为交流多电平电压；蓄电池支路则根据功率分流算法输出电压，以控制电池支路的功率。系统的三相结构如图1b所示，实际为单相结构的星形连接。

从拓扑图可以看到，该拓扑除了具有多电平电路的一般优点以外，还具有非常高的模块化特性，因此容易通过增加级联数增大电压和大容量。此外，当某个模块故障时，可以使用半桥变换器旁路此模块，实现容错运行，也可以容易地替换维修。最后，相比于传统的MMC电路，因为该拓扑每相只有一个桥臂，所以可以节省一半的开关管。

2.2PWM调制方法

由于拓扑中存在多个模块级联，因此在PWM调制过程中，根据电压指令产生多电平交流电压的同时还需要实现内嵌的电压均衡。为了达到以上目的，本文提出了一种特殊的载波层叠PWM调制方式实现。对于一个直接连接在直流母线上的级联支路，当支路放电时，这种PWM调制方式的原理如图2所示。其调制过程描述如下:

（1）对各个基本模块所带储能介质模块的电压按照从大到小的顺序进行排序

（2）按照排序顺序，将各模块对应的载波依次叠放，电压低的模块的载波在上层。其中每一个模块对应载波的峰峰值就是这个储能模块的端电压。

（3）载波和参考波绝对值相比较，当参考波的绝对值较大时，对应模块输出高电平，反之则对应模块输出低电平。如此即可得到此支路上各个基本模块的PWM信号。

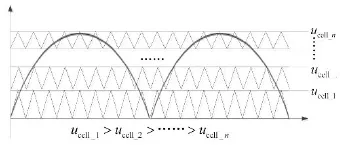
图2 主动均压的载波层叠PWM调制方法（放电情况）Fig.2 modified carrier-cascaded PWM method for active voltage balance (during discharging)

在调制过程中，支路放电时，电压更高的模块放电时间更长而电压较低的模块放电时间较短，运行一段时间即可实现支路各模块之间的电压平衡。拓扑充电时，只需要将排序顺序改为升序。支路电压可以按照下面的公式计算得到:

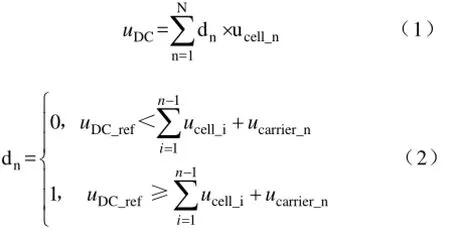
其中uDC为直流母线电压，ucell_n是支路中第n个储能模块的电压，dn是开关函数，表示的是第n个模块的开关装填，uDC_ref是直流母线的参考电压。ucarrier_n是第n个模块的载波信号。N为级联数。

需要说明的是，图2给出的实际是超级电容支路的调制过程。因为H桥的开关状态由交流电压的极性决定，因此超级电容支路的电压参考值实际上为交流参考电压的绝对值。电池支路的电压参考值由功率分流算法给出，但过程相同。

3 功率分流算法

设计功率分流算法是为了使超级电容和蓄电池的特点能够充分互补:使用超级电容吸收负载电流的波动分量，短时间内弥补蓄电池功率较低的缺点，同时超级电容的容量也必须充分利用；使用电池作为主要的储能器件，输出长时间的稳定的功率。

为了达到这些目标，最简单、也被大多数文献采用的方法是使用低通滤波器（LPF）将功率指令中的高频分量滤除，功率的低频分量由电池支路发出，高频分量由超级电容支路发出。因为低通滤波器的存在，电池支路电流中将不存在高频分量。但是这种方法没有考虑超级电容的SOC，因此超级电容的容量可能无法充分利用，或者SOC较快达到安全极限值。例如，功率指令为连续的具有陡上升沿和缓下降沿的锯齿波时，超级电容的 SOC将不断下降直到安全下限，使拓扑停止工作，但这时蓄电池中还有充足的电量或储能空间。

为了克服低通滤波器法的缺点，可以将电池支路的功率根据超级电容的SOC来设定，即Pbat= f(SOCsc)[17]。典型的f(SOCsc)函数形式是单调递减带有上下限的线性函数，如图3所示。当功率指令值为正时电路放电，为负时电路充电。所以，当超级电容的SOC比较低时，Pbat将会增大，分担更多的功率，并且给超级电容充电。因此，这种功率分流算法在大多数情况能够将超级电容SOC限制在安全范围内。同时，因为超级电容的SOC变化缓慢，电池支路的功率指令将非常平滑。但如果储能系统的功率指令超过f(SOCsc)的限值一段时间，SOCsc也会超出安全范围。这是因为采用这种方法，蓄电池短时间大电流充放电的能力没有得到充分利用。

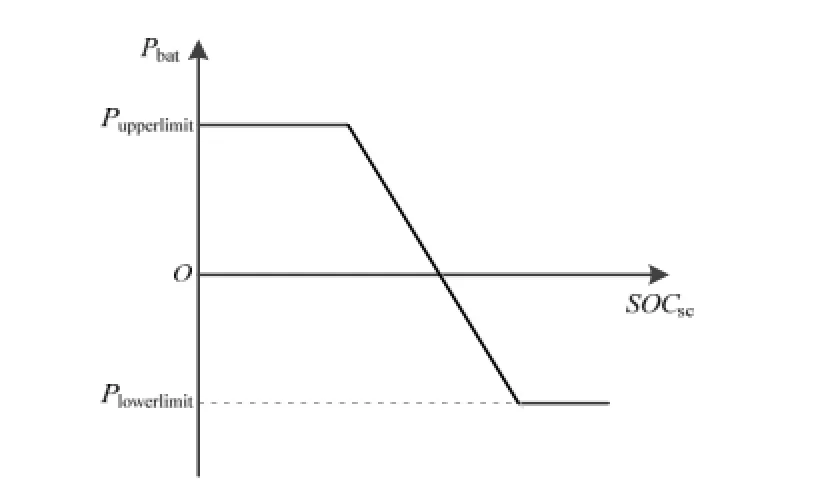
图3 电池支路功率指令-超级电容SOC曲线Fig.3 power reference of battery branch vs super capacitors’ average SOC

当电池支路的功率指令确定后，电池支路的电流指令也可以随之确定（因为线路电阻极小，可以认为电池支路的电压与超级电容支路的电压基本相等，由此可以计算出电池支路的电流指令）。使用PI调节器闭环控制电池电流，就可以给出电池支路的参考电压值。本文通过仿真和实验比较了这两种种功率分流算法的优劣。

4 仿真结果

本文在MATLAB/SIMULINK平台上完成了拓扑的三相交流电源充放电仿真，模拟储能系统的并网充放电。每相拓扑取级联数N=4，电池采用12V 4.5Ah铅酸蓄电池，初始SOC为70%；超级电容采用16.2V耐压70F超级电容，安全电压范围为10-15V，初始电压为14V。

并网控制采用了锁相环和电网电压定向的dq轴电流解耦控制的方法，由于此方法比较成熟，且被许多文献采用，在此不再赘述。有功指令为幅值为100W正负波动的方波，无功指令为0时，并网三相电流和电压如图4所示。说明该拓扑具有较好的动态响应和较低的谐波含量，并且可以将输出控制为单位功率因数。

在进行功率分流算法仿真时，使用了如图5所示的由功率指令得到的线电流指令。图5中的功率指令是由贵州省某地的日负荷曲线和24小时光伏发电数据相减得到的。为了适应仿真的时长和设计容量，将两个周期48小时的数据压缩到了2 400秒中，并且将幅度进行了等比例缩减，并根据并网电压，将功率指令折合为系统线电流有效值的参考值，即图5中所示2 400秒的电流指令。

在这样的功率指令下，两种功率分流算法的仿真结果如图6a、6b所示。仿真结果由所有电池的平均SOC、所有电容的平均电压和电池支路电流三个波形组成。

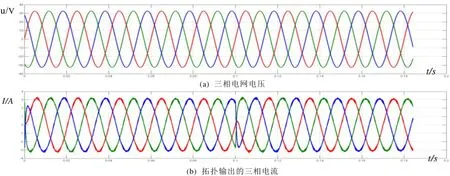
图4 拓扑并网运行电压电流波形Fig.4 grid voltage and topology output current during grid connection

图5 由功率指折合的线电流有效值指令Fig.5 effective values of current reference of topology

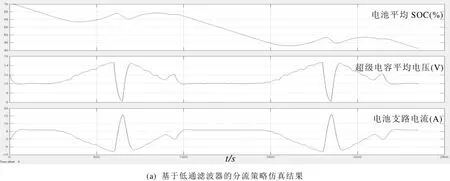
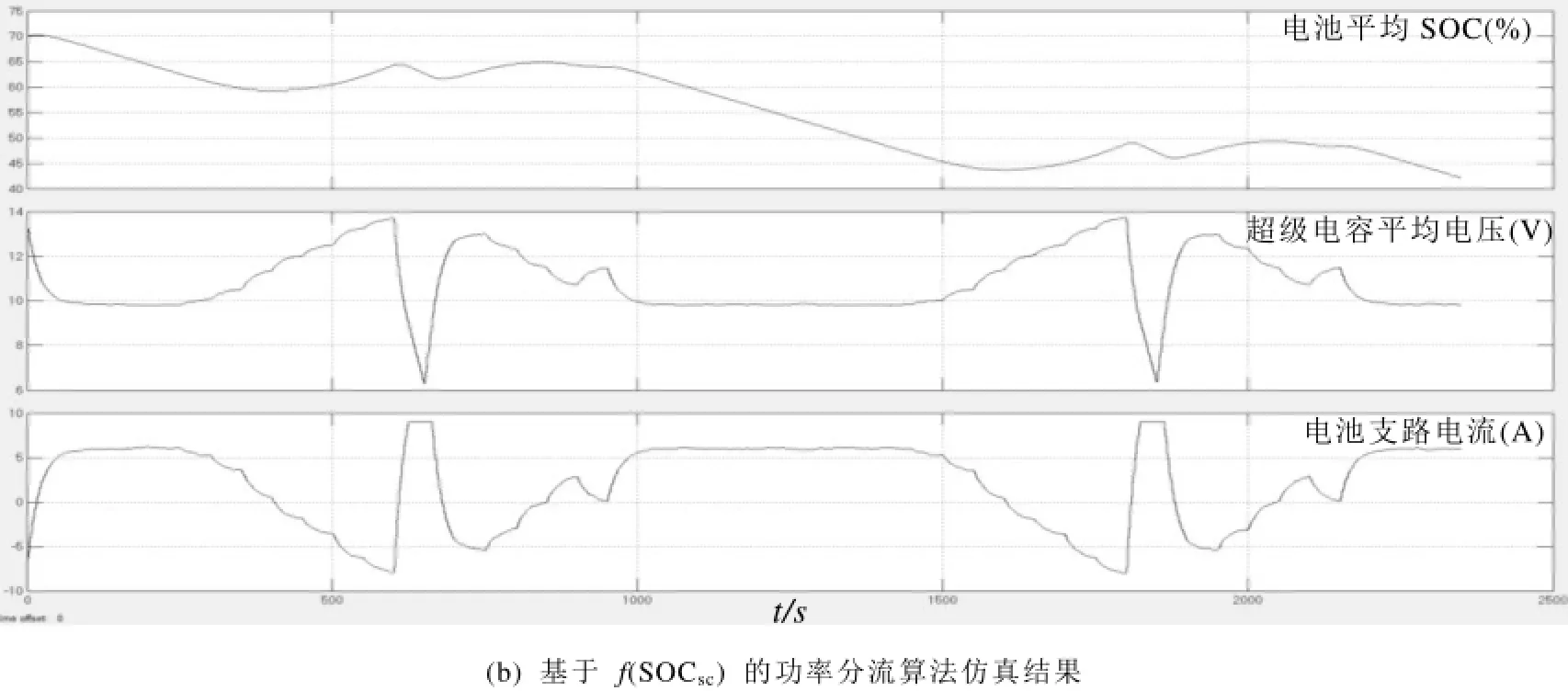
图6 两种功率分流算法的仿真结果比较Fig.6 comparison of two power sharing algorithm

在图6a、6b中，约600秒和750秒处各出现了一次超级电容的电压尖峰，但低通滤波器法的最高电压已经非常接近安全限值15V，而根据超级电容SOC设定电池功率的方法的最大电压尖峰不超过14V，这是因为电池对超级电容的SOC及时做出了反应，帮助超级电容工作在安全范围内。

当功率指令为1Hz锯齿波（直流偏置为1，振幅为2，具有缓的上升沿和陡的下降沿），两种功率分流算法的不同更加明显。结果如图7a、7b所示。如图7a所示，在低通滤波器法控制下，因为功率分流没有考虑电池和超级电容的SOC，超级电容电压将很快达到安全限值，这是因为缓上升沿（即放电过程中）主要由电池响应，而陡下降沿（即充电过程）主要由超级电容响应。而在图7b中可以看到，超级电容电压将稳定在某一值，使蓄电池输出功率稳定在功率指令的平均值。

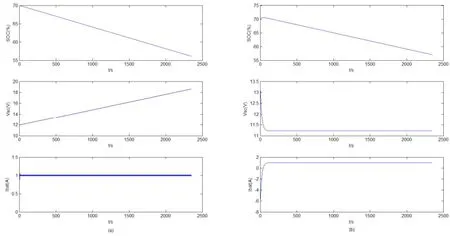
图7 锯齿波功率指令下两种功率分流算法的仿真结果比较Fig.7 comparison of two power sharing algorithm with saw tooth wave power reference

5 实验结果

除仿真之外，本文还搭建了小容量的实验平台，获得了基于低通滤波器的功率分流算法的实验结果。实验平台如图8所示，选用的蓄电池为12V 4.5AH的铅酸蓄电池，超级电容为16.2V耐压66.7F，级联数为4。在此实验平台上，完成了混合储能并网充放电的实验。

首先，实验验证拓扑的基本功能，如图9a、9b。图9a显示的是并网成功后，拓扑三相电压和A相电流波形，此时有功指令为50W，无功指令为0。电压波形说明拓扑能够输出多电平的交流电压；电流波形说明该拓扑具有非常好的谐波抑制特性。输出电流之所以和输出电压有一定相位差，是因为并网时在电路中连接了滤波电感，导致输出电压和网侧电压有一定相位差，但是电流相位需要保持和网侧电压一致。图9b显示的是超级电容电压的均衡过程，证明了均衡算法的有效性。拓扑并网运行的基本功能得到验证，在此基础上，进行功率分流算法的实验。

图8 储能装置实验平台Fig.8 experimental platform of energy storage

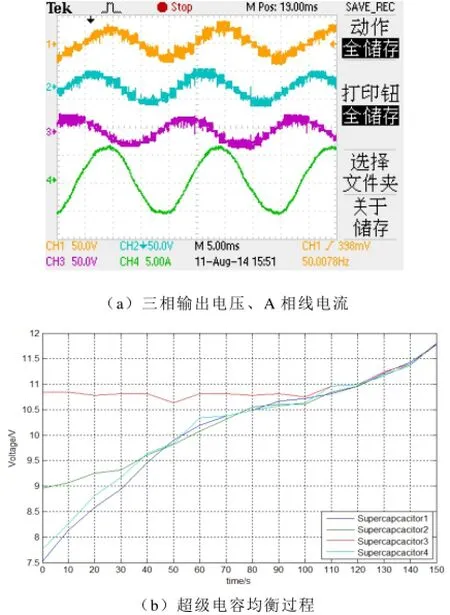
图9 拓扑基本功能实验验证Fig.9 basic function verification of proposed topology

然后，通过短时间实验验证功率分流算法的性能。采用基于低通滤波器的功率分流算法时，短时间实验结果如图10所示。图10a显示的是直流母线电流，图10b和10c显示的分别是A相蓄电池支路和超级电容支路的电流。如图10a所示，因为此拓扑实际为3个单相系统星形连接，因此即使功率指令没有波动，直流母线上也会有二倍基频的波动，由于低通滤波器的存在，此时超级电容电流则被迫吸收了直流母线电流中波动的成分，电池电流的方向则不变，且接近恒流，如图10b所示。此外，由于低通滤波器的存在，当功率指令高频波动时，电池支路的电流指令仍然为低频，将电池支路的电流也控制为低频。因此，在短时运行中，这种功率分流算法使电池的工作状态得到了改善。当采用超级电容SOC函数功率分流算法时，因为电路结构和底层控制相同，所以短时间实验结果与低通滤波器法是完全相同的，在此不再列出。

图10 低通滤波器功率分流法的短时间实验结果Fig.11 short time experiment result of low pass filter power sharing strategy

最后，如仿真结果所显示，两种方法的差别在长时间实验中才能显示出来，因此需要进行长时间实验验证。长时间实验的功率指令曲线如图11a所示，两种分流方法的结果分别如图11b、11c所示。

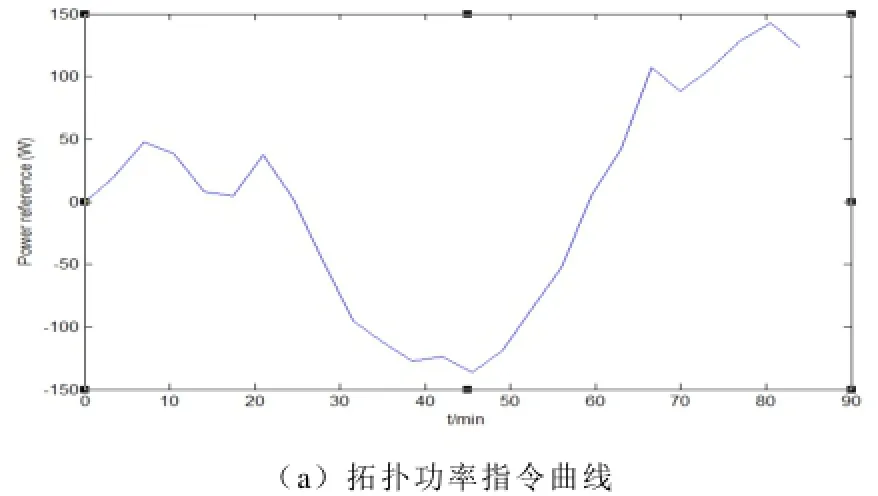
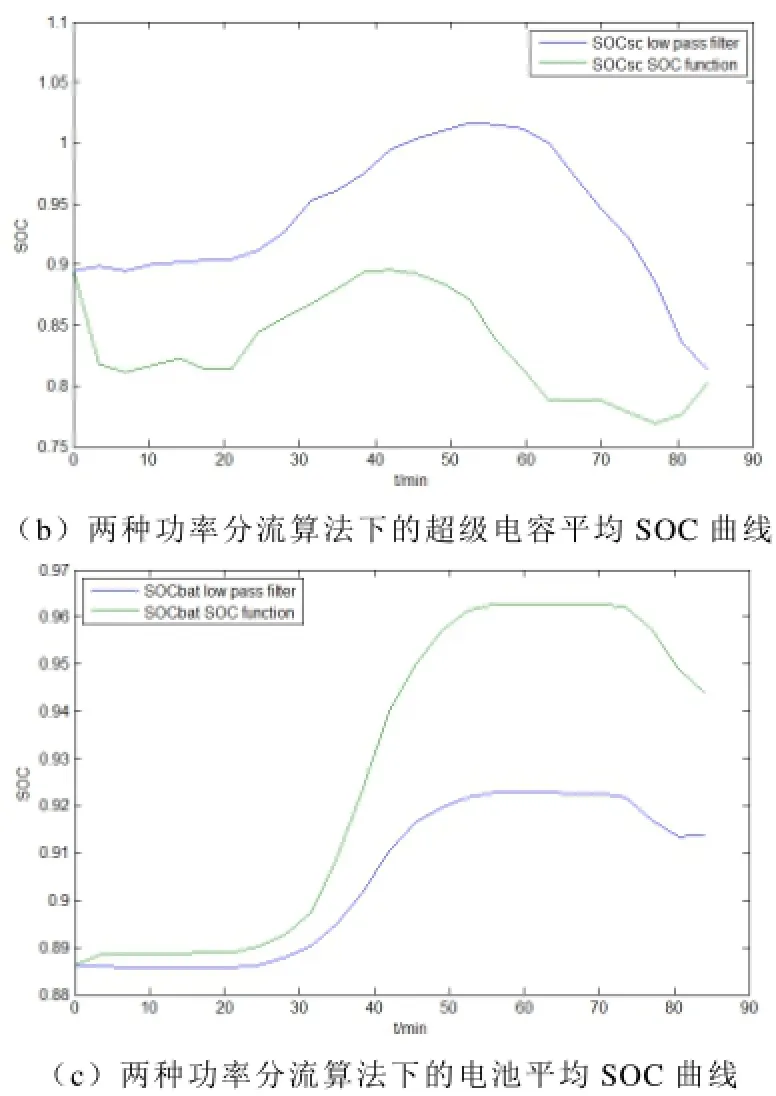
图11 功率分流算法长时间运行的实验结果Fig.11 experimental result of two power sharing alogrithms’ long time operation

从实验结果中可以看到，低通滤波器法的超级电容SOC有大于1的情况，电压说明突破了安全限值15V，但尚未导致损坏。而超级电容SOC函数分流方法得到的电容SOC则相对平稳。对应的，充电时，低通滤波器法控制下的电池SOC增长较少，而超级电容SOC函数法控制下的电池SOC增长较多，说明超级电容SOC函数法对电池的容量利用更加充分。因此，通过仿真和实验证明，超级电容SOC函数分流方法在本拓扑中优于低通滤波器分量方法。

6 结论

本文提出了一种新型混合储能拓扑，能够通过载波层叠调制方法实现的储能模块电压均衡。此外，该拓扑具有谐波含量低，高模块化特性，易于容错运行和扩展至高压大容量等优点，因此也具有较大的实用意义。

本文搭建了小容量平台上进行了实验，证实了提出拓扑所具有的优点，也证明了超级电容支路对电池寿命有保护作用。

在提出拓扑的基础上，通过实验和仿真，对比了低通滤波器法和超级电容SOC函数法两种功率分流算法。仿真和实验结果证明，第二种策略更能够充分发挥超级电容和蓄电池的性能。

[1] 孔令怡, 廖丽莹, 张海武, 等. 电池储能系统在电力系统中的应用[J]. 电气开关, 2008(05): 61-62.

Kong Lingyi, Liao Liying, Zhang Haiwu et al. Application of Battery Energy Storage System in Power System[J]. Electric Switchgear, 2008(05): 61-62.

[2] 田军, 朱永强. 储能技术在分布式发电中的应用.电气技术[J]. 2010(08): 第28-32+42页.

Tian Jun, Zhu Yongqiang. Application of Energy Storage Technologies in Distributed Generation[J]. Electrical Engineering, 2010(08): 28-32+42

[3] 常乐 等. 储能在能源安全中的作用[J]. 中外能源, 2012(02): 第29-35页.

Chang Le, Zhang Minji, Liang Jia, Sun Yangzhou. The Function of Energy Storage in Energy Safety[J]. Sino-Global Energy, 2012(02): 29-35

[4] 桑丙玉, 陶以彬等. 超级电容-蓄电池混合储能拓扑结构和控制策略研究[J]. 电力系统保护与控制, 2014(01): 1-6.

Sang Bingyu, Tao Yibin, et al. Research on topology and control strategy of the super-capacitor and battery hybrid energy storage[J]. Power System Protection and Control, 2014(01): 1-6.

[5] 于芃, 赵瑜等. 基于混合储能系统的平抑风电波动功率方法的研究[J]. 电力系统保护与控制, 2011(12): 35-40.

Yu Peng, Zhao Yu, et al. Research on the method based on hybrid energy storage system for balancing fluctuant wind power[J]. Power System Protection and Control, 2011(12): 35-40.

[6] 卢芸, 赵永来. 基于模糊神经网络风电混合储能系统优化控制[J]. 电力系统保护与控制, 2014(06): 113-118.

Lu Yun, Zhao Yonglai. Optimal control in a wind power hybrid energy storage system based on fuzzy neural network[J]. Power System Protection and Control, 2014(06): 113-118.

[7] 张纯江, 董杰等. 蓄电池与超级电容混合储能系统的控制策略[J]. 电工技术学报, 2014(04): 335-340.

Zhang Chunjiang, Dong Jie, et al. A Control Strategy for Battery-Ultracapacitor Hybrid Energy Storage System[J]. Transactions of China ElectrotechnicalSociety, 2014(04): 335-340.

[8] Jayasinghe, S. D. G, Vilathgamuwa, D. M., and Madawala, U. K.: A new method of interfacing battery/super capacitor energy storage systems for distributed energy sources[C]. IPEC 2010, pp. 1211-1216.

[9] Monteiro, V., Pinto, J. G., Exposto, B., Goncalves, H., Ferreira, J. C., Couto, C., and Afonso, J. L.: Assessment of a battery charger for Electric Vehicles with reactive power control[C]. IECON 2012, pp. 5142-5147.

[10] Qian, H., Zhang, J., Lai, J., and Yu, W.: A highefficiency grid-tie battery energy storage system[J]. IEEE Transactions on Power Electronics, 2011, 26(3), pp. 886-896.

[11] Lee, Y., and Cheng, M.: Intelligent control battery equalization for series connected lithium-ion battery strings[J]. IEEE Transactions on Industrial Electronics, 2005, 52(5): 1297-1307.

[12] Cassani, P. A., and Williamson, S. S.: Feasibility analysis of a novel cell equalizer topology for plug-in hybrid electric vehicle energy-storage systems[J]. IEEE Transactions on Vehicular Technology, 2009, 58, (8), pp. 3938-3946.

[13] A Hillers, and Biela, J. Optimal design of the modular multilevel converter for an energy storage system based on split batteries[C]. EPE 2013, pp. 1-11.

[14] Martel, T., and Rufer, A.: Electric vehicle driving and fast charging system based on configurable modular multilevel converter (CMMC)[C]. EPE 2013, pp. 1-10.

[15] Wei Li, Joos, G.: A power electronic interface for a battery supercapacitor hybrid energy storage system for wind applications[C]. PESC 2008, pp. 1762-1768.

[16] Yu Zhang, Zhenhua Jiang.: Dynamic Power Sharing Strategy for Active Hybrid Energy Storage Systems [C]. VPPC 2009, 558-563.

[17] 丁若星. 微电网中的混合储能系统研究[D] 清华大学2014. Ding Ruoxing. Research on Hybrid Energy Storage System in Micro Grid[D]. Tsinghua University 2014.

A Novel Hybrid Energy Storage Topology and its Power Sharing Algorithm

Chang Fengqi Zheng Zedong Li Yongdong
（State Key Laboratory of Power Electronics and Motor Control, Department Electrical Engineering, Tsinghua University Beijing 100084 China）

Topology and power sharing algorithm are two important issues in hybrid energy storage research. In this paper, a novel hybrid energy storage topology based on modular multilevel converter is proposed and a modified carrier-cascaded PWM method is used to realize active voltage balance between energy storage modules. In the research of power sharing algorithm, disadvantages of low pass filter method are summarized, which is the most commonly used strategy for power sharing. A novel power sharing strategy is compared to this method by simulation and experiment. Simulation result is gained on MATLAB/SIMULINK platform. Both short time and long time operation experiment result are gained on a low capacity experimental energy storage device.

Hybrid energy storage, power sharing, active balance, MMC topology

TM46

常丰祺 男，1991年生，硕士研究生，研究方向为电力电子储能变换器和电池管理系统。

国家自然科学基金项目（51107066）。

2014-08-10

郑泽东 男，1980 年生，副教授，研究方向为电力电子与电气传动。